Конспект урока по алгебре в 11 классе, на тему: "Графический способ решения уравнений, неравенств, систем уравнений и систем неравенств".
Конспект урока, представляет собой профильную подготовку к экзамену. В данный материал собраны, самые лучшие задания по параметрам и уравнениям.
Около 20 с большим заданий. Возможно также, и использовать для выполнения заданий домашней контрольной работы. В 11 классе. Также информация подойдет для репетитора.
Опять про параметры..doc
Графический способ решения уравнений, неравенств,
систем уравнений и систем неравенств.
Задача 1. Найти все значения a, при которых уравнение
имеет единственный корень.
65
x
2
x
a
2
2
ax
x
. Вершина (максимум) в точке
)4,3(
. Точки пересечения с осью OX
. Область
, то есть
)2,3(
65
x
2
x
5
,1
)(
xy
Решение.
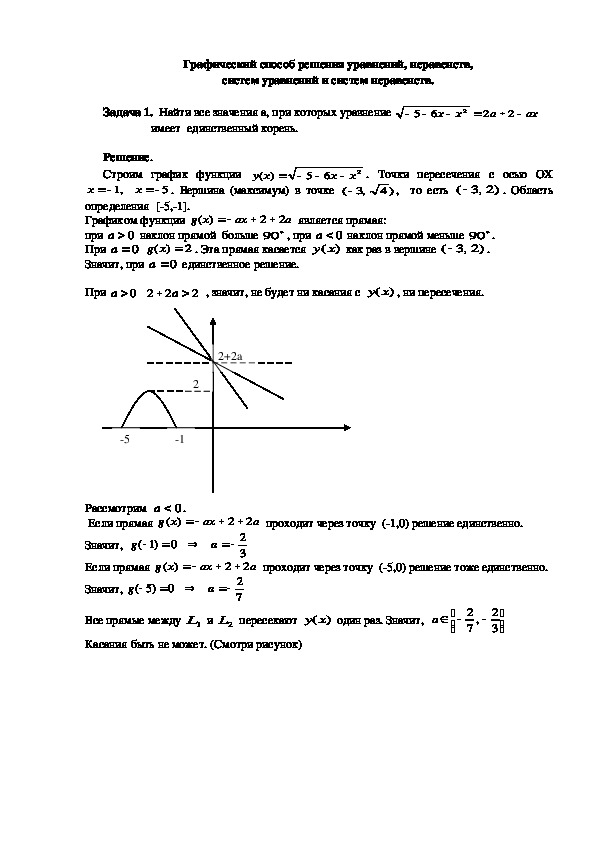
Строим график функции
x
определения [5,1].
Графиком функции
наклон прямой больше
при
При
Значит, при
)( xg
0a
22
90 , при
. Эта прямая касается
2
единственное решение.
0a
0a
xg
)(
ax
a
является прямая:
0a
)(xy
наклон прямой меньше
как раз в вершине
)2,3(
90 .
.
При
0a
a
22
2
, значит, не будет ни касания с
)(xy
, ни пересечения.
2+2а
2
5
1
Рассмотрим
Если прямая
0a
xg
)(
.
Значит,
g
)1(
0
Если прямая
xg
)(
ax
Значит,
g
)5(
0
a
a
22
2
3
22
2
7
ax
a
проходит через точку (1,0) решение единственно.
a
проходит через точку (5,0) решение тоже единственно.
Все прямые между
2L пересекают
Касания быть не может. (Смотри рисунок)
1L и
)(xy
один раз. Значит,
a
2
7
,
2
3
1L
2L
2
5
1
2 a
2
2
a
0
a
2
2
2
противоре
чие
2
a
0
a
2
2
2
противоре
чие
5
1
5
1
2 a
2
Задача 2. Найти все значения a , при которых функция
ровно три нуля.
Решение. Следует выяснить, при каких a уравнение
корня.
Ответ:
a
2
7
,
2
3
и
0a
xf
)(
22
x
2
a
ax
имеет
22
x
2
a
ax
0
имеет три
Преобразуем уравнение к виду
x
2
a
2
ax
4
и построим оба графика. Один из них
имеет вид буквы «w», причем при изменении параметра точки пересечения с осями
координат
,0
2
a
2
,
2
a
2
0,
скользят по осям. Второй график – прямая с постоянным
наклоном, смещающаяся по оси OY. Из рисунка видно, что графики будут иметь только
три точки пересечения, если прямая
y
займет положение 1 или 2.
ax
4 y
2
1
x
По рисунку видим, что ситуация 1 произойдет, если
y
ax
4
в точке
x
2a
2
примет
значение 0, то есть при
2a
. Положение 2 прямая займет, если
2a
2
, то есть при
4
a
x
4
0a
или
5.0a
. В случае
0a
графики
y и
x
y имеют единственное
пересечение, значит, функция
5.0a
2a
или
.
xf
)(
22
x
2
a
ax
имеет ровно три корня при
Ответ:
5.0a
2a
Задача 3. Найти все значения a, при которых уравнение
)5
5
5
a
a
a
x
x
x
(
2
2
имеет единственный корень.
Решение.
b
x
x
2
b
или
2
x
2
b
b
x
xb
2
a
5
, тогда
Обозначим
b
x
Строим два графика
b
y
при
b
2
x
2
x
при
x
xb
при
2
b
x
y
2
2
b
и
x
b
b
x
b
b
x
Единственное пересечение будет, когда вершина параболы коснется дна «корыта», то есть
при
Но при
и пересечений уже будет три.
«корыто» превращается в угол
2
b
0b
2b
или
2
0
b
b
x
y
2 Задача 4. Найти все значения a, при которых уравнение
хотя бы один корень из
)5,2
log 5
(
ax
)8
x
2
имеет
Ответ:
7a
2
)
x
8
2
2
x
a
5(
a
)3
)8
x
, тогда
t
t
3,0t
.
должно иметь хотя бы один корень
(
a
)3
t
(
y и
y
t
a
2t
)3
(
5
Решение:
(
ax
log
x 5
Обозначим
t
5,2x
, то
Так как
Значит, уравнение
2
t
Строим графики
промежутке
прохождения прямой через точку
A
3,0
(3:
3
)3
9
a
a
3,0t
.
. Пересечения будут начиная с момента касания в точке B до
и ищем пересечение прямой и параболы в
)9,3(A
.
B
:
2
t
t
(
a
)3
0
D
0
a
13
4
9
А
В
3
Ответ:
13
4
3,
Задача 5. Найти все значения a, при которых система уравнений
y
)5
x
3
2
ay
)5
x
(
2
2
2
a
(
x
имеет более двух решений.
Решение.
(
x
)5
2
(
ay
)5
2
a
2
окружность с центром
,5(
a
)5
радиуса
R
a
y
x
x
2
3
,1
2
x
,5
x
x
3
3
Более двух пересечений окружности и прямой может быть:
1) радиус окружности
2) окружность касается или пересекает AB и AC
OA
R
Рассмотрим эти случаи.
1)
2) Рассмотрим пересечение прямой AB и окружности.
)35(
)55
OA
R
a
a
a
(
2
2
4
2
a
решений
нет
Линия центров
C
B
D
A
5
2
x
x
a
5
y
2
)5
5
2
a
(
Получается, что окружность всегда касается прямой AB в точке
Значит, прямую AC она должна пересекать дважды.
2
1
x
ay
(
)5
ax
y
2(
)6
)5
)5
D
0
a
a
x
x
(
(
2
2
2
2
2
2
D
)5,5(
.
2
5
x
17(2
x
61(
)
0
D
4
a
2
8
a
16
0
)2
a
1
12
a
a
1,
Заметим, что если центр окружности будет ниже прямой AB , пересекать прямую AC
(*)
,5
5 окружность уже не будет.
Центр ниже AB :
решения.
5
a
5
a
0
. Значит, в (*) надо оставить только положительные
Ответ:
a
1
,5
Задача 6. Найти все значения a, при которых неравенство
x
ax
23
2
1
x
верно для всех x .
Решение.
Перепишем неравенство в виде
x
1
2
x
x
x
1
2
)(
xg
1
1
. Строим неподвижный график
“опрокинутый” угол
3
x
,1
x
,1
2
x
x
x
y
,
xf
)(
23
ax
. Обозначим
ax
23
2
x
a
,23
x
,23
2
a
x
a
a
x
)(xg
и график
, вершина которого
)(xf
( aO
, который представляет из себя
)3,
скользит по прямой
3y
.
y
g(x)
x
1
А
2
f(x)
x
1
2
ax
Чтобы неравенство
)(xg
x
должен быть для всех x выше, чем график
. Это будет выполняться, если левая
A
a
часть угла будет находиться правее точки
5,1a
координаты точки А, получим
. Это то значение параметра, когда графики
имеют единственную точку пересечения А. Значит, при
выполнялось для всех x , график
)(xf
получаем требуемое.
. Подставим в
)2,1(
5,1a
23
xf
)(
23
2
x
5,1a
Задача 7. Найти все значения a, при которых система неравенств
2
x
x
имеет хотя бы одно решение.
3
2
a
y
a
4
y
Ответ:
2
2
Решение.
x
y
4 четыре ветви гиперболы.
окружность,
y
a
x
y
2
2
3
a
x
3
a
область внутри круга. 0a
0a
0a
0a
При
Так как при
0a
.
Пусть
0a
2
0a
x
y
0
y
0
x
первое неравенство системы неверно, то рассмотрим только
2
2
2
0a
.
значит, одно решение
x
y
,0
0
x
y
0
y
0
x
2
x
y
2
4
a
x
y
3
a
имеет два решения, если будет касание (то
Из рисунка видно, что система
x
есть
2
aD
0D
). Если
2
3
a
y
4
a
x
64
a
y
2
2
6
2
x
2
16
a
2
x
3
a
4
x
(
aa
4
)64
0
a
0D
, то решений у системы уже множество. Значит,
0D
.
2
3
xa
16
a
2
0
4
,64
)
Ответ:
,0a
a
,22
)
Задача 8. Найти наименьшее значение параметра a , при котором система неравенств
имеет единственное решение.
(
y
1
)24
a
2
x
1
80
1
a
a
x
y
)
(
2
2 Решение. Второе неравенство задает полуплоскость, расположенную ниже прямой
. Первое неравенство задает круг с переменным
x
, то есть
x
5.0
5.0
2
1
y
y
центром в точке
O
1,24(
a
a
)
переменного радиуса
R
a
1
80
. Чтобы
a
a
4
x
1
y
x
5.0
Исключая из уравнений параметр, получим уравнение прямой центров
выяснить, как перемещается этот круг, найдем линию центров, то есть прямую, по которой
“катится” круг. Запишем координаты центра
y
Значит, круг “катится” по прямой, параллельной границе полуплоскости. Тогда ясно, что
единственное решение системы будет в том случае, когда радиус круга станет равным
расстоянию от центра круга до прямой
, то есть
dR .
x
5.0
5.0
1
y
y
B(0;1)
d
С
A(0;0,5)
y=0.5x+1
y=0.5x+0.5
x
Найдем
АВ
5,0
tg
ABC
расстояние
5,0
cos
ABC
d :
1
5
1d
5
в
треугольнике
АВС
. Значит,
. Остается решить
уравнение
a
1
80
1
5
a
,3
a
5
.
Ответ:
a
a
,3
5
Решение неравенств с параметром методом интервалов.
Задача 9. Найти все значения a, при которых неравенство
9x
ax
ax
3
2
x
верно для всех
Решение.
0
Отсюда
x
,0
x
3
a
a
x
24
2
a
2
Преобразуем:
Рассмотрим случаи
1) пусть
0
24
2
6
)3
,
x
ax
axx
(
0D
, то есть
0D
.
24
a
Случай
можно рассмотреть отдельно:
a
2
0a
2
24
x
6
x
3
0
решений, больших 9, нет.
Чтобы для всех было
верно, должно быть , то
есть
0
3
a
3
a
если
0
если
Решений, больших 9, нет
2) пусть
2
a
24
0
, то есть
a
2
x
ax
6
0
Корни
a
x
1
,24
a
2
2
a
24
24
a
x
2
24
2
a
2
x
6
x
, то корни одного знака, причем:
Так как
1
0
,0
если
, то
,0
0
, то
если
2
x
x
0
0
0
0
a
a
x
x
x
1
x
1
x
1
x
1
2
2
2
2
( по теореме Виета)
0
0
3
a
1x
0
1x
2x
1x
2x
3
a
2x
3
a
a
24
тогда
для
всех
неравенство
верно
Этот случай
уже
рассмотрен Решаем неравенство
a
Случай
x
1
,0
x
2
,0
a
2
a
2
24
9
a
29
3
0
ничего не даст.
Ответ:
a
1
3
,
29
3
)(
)3
ax
0
ax
ax
Задача 10. Найти те значения a , при которых система неравенств
(
Решение:
Пусть
не имеет решений.
2
a
4
0a
x
, тогда из второго неравенства
2
a
a
x и
a
x
3
Из первого неравенства
4
a
В этом случае, куда бы ни попало число
Пусть
Пусть
0a
0a
, тогда второе неравенство
, тогда из второго неравенства
4 , решения всегда будут.
x
0 , значит, решений нет.
a
4
4
a
, либо
x
1
2
, но
a
4
a
0a
4
a
3
3
2
a
a
a
Решаем неравенство
Решений не будет, если либо
a
a
4
a
4
Решаем неравенство
a
)0,2(a
остается
2
, значит, так быть не может.
a
4
2
a
a
0
a
)0,2(
)
,2(
. При условии
0a
a
2
a 3
a
2
a 3
a
a 4
a
a
2
a 3
a
4
a
2
a 3
a
a
Задачи на исследование корней квадратного уравнения.
Ответ:
0,2(
Задача 11. Найти все значения a, при которых уравнение
имеет два различных корня и только меньший из них принадлежит (2, 3]
)1
a
x
(
2
2(
a
)3
ax
0
Решение.
Два различных корня
D
0
a
9
16
a
1
Запишем корни:
a
2
x
1
Если
1a
, то
3
(2
a
x
1
9
2
a
x
2
3
(2
a
16
a
)1
9
16
a
)1
x
.
2
Составим систему:
Решаем (*)
2
3
3
x
2
x
1
или
2
2
a
3
16
(2
a
)1
3
a
a
(2
2
16
)1
a
9
3
(*)
a
9
3
.
(**)
2
a
3
(2
a
16
a
)1
9
3
83
a
(2
a
16
a
)1
9
0
8
a
3
16
a
9
a
1
9
16
1 Неравенство решений не имеет, значит, система тоже.
Рассмотрим случай, когда
Составим систему:
1a
, тогда
x .
2
x
1
3
x
1
2
x
3
2
или
2
a
2
2
16
3
(2
a
)1
3
a
(2
a
16
)1
a
9
3
(*)
a
9
3
.
(**)
Решаем (*):
2
a
3
(2
a
16
a
)1
9
3
83
a
(2
a
16
a
)1
9
3
16
a
83
a
9
a
0
0
9
16
Значит,
Решаем неравенство из (**):
)1,0(a
решение (*)
1
2
a
3
(2
a
16
a
)1
9
3
83
a
(2
a
16
a
)1
9
0
16
a
8
a
9
3
a
1
9
16
1
Значит,
a
9
16
1,
. Это с учетом того, что
1a
Решаем второе неравенство из (**)
2
a
a
9
3
(2
a
16
)1
2
2
a
7
(2
a
16
)1
a
9
0
16
a
27
9
a
a
1
9
16
a
Значит,
1
9
16
1,
.
Собираем решения:
)1,0(a
и
a
9
16
1,
Значит, общее решение
)1,0(a
. Задача 12. Найти те значения a , при которых уравнение
9(3
3(
)1
0
3
x
x
)
1
2
2
a
a
a
имеет ровно один корень.
Ответ:
)1,0(a
Решение.
0D
и все.
Ответ:
a
a
,0
1
log
3
7
Задача 13. При каких значениях a модуль разности корней уравнения
принимает наибольшее значение.
2
2
4
a
0
6
x
12
a
x
Решение.
2
2
a
1
x
1
2
3
наибольшее
x
2
2
4
a
a
03
x
x
(
)(
x
1
xx
2
x
21
D
xf
)(
xg
)(
)(
xg
)
Используя теорему Виета, получим:
g
g
4 2
16
a
a
)3(
g
,0
)1(
12
g
x
1
f
2
x
1
16
)
(
2
2
. Обозначим
наибольшее
x
xx
21
4
2
2
. Находим наибольшее значение этой функции на
8
a
наибольшеезначение.
)2(
4
g
3,1
.
Ответ:
2a
Задачи на наибольшие и наименьшие значения функций.
Задача 14. Найти те значения a , при которых наибольшее значение выражения
равно числу корней уравнений
ax
75,0
1
2
3
x
x
x
a
.
Решение. Строим график функции
)(
xy
3
x
x
x
3
2
x
,3
x
2
,
x
x
x
3
3
и прямую
y .
a Вершина параболы находится в точке
3
2
,
9
4
..
Из рисунка видно, что при
0a
и при
При
0
a
9
4
3 корня, и при
a
9
4
,
9a
4
0
a
уравнение
x
1 корень.
1 корень
2 корня
0
3 корня
9
4
3
x
a
имеет 2 корня.
1 корень
x
2
)(
xy
ax
Рассмотрим функцию
Поэтому наибольшее значение этой функции достигается только в точках «излома», то
x . Найдем эти значения:
есть при
y
75,0
Число корней – один:
. Значит, наибольшим будет
1x
и
1
a
и
75,01
. При
a
a
. Но при этом
. Пусто.
или
или
0a
)1(y
75,0
)(
ay
75,0
)(xy
x
)1(
.
1
1
a
a
2
1
.
5
4
3a
4
9a
4
Число корней – два:
75,0
2
1
a
Число корней – три:
75,0
3
1
a
a
9
4
или
3a
4
Значит, подходит
9a
4
a
19
4
или
11a
4
. Но при этом
0
a
9
4
. Пусто.
Ответ:
9a
4
2
x
6
ax
10
на
Задача 15. Найти те значения a , при которых наибольшее значение функции
xf
)(
3
Решение.
Преобразуем:
)
x
(3
a
3(
a
2
Значит, вершина параболы с учетом модуля
)10
3,
(
a
a
4x
может достигаться либо в вершине, либо при
, или при
не превосходит 14.
2,4
)(
xf
. Наибольшее значение
2x
)10
10
ax
6
3
x
.
2
2
2
f
38
)4(
24
a
14
1
a
f
)2(
2
12
a
14
1
a
52
24
4
3
4
3
2
3
a
10
14
2
a
Общим решением является
1a
Ответ:
1a
Задача 16. Найти те значения a , при которых наибольшее значение функции
не превосходит 1. Ответ:
)(
xf
2
3a
x
2
x
2
5
ax
3
5
x Задача17. Найти те значения a , при которых наибольшее значение функции
)(
xf
больше либо равно 1.
ax
x
2
Ответ:
Задача 18. Найти те значения a , при которых наименьшее значение функции
)(
xf
больше 1.
ax
2
7
8
x
x
2
3a
4
Решение.
)(
xy
2
x
2
x
x
2(
ax
7)28(
7)8
a
при
x
7
1
7
1
x
x
при
Наименьшее значение достигается либо в точках излома
этих парабол.
y
)1(
2
a
2
a
1
a
x
,1 x
7
, либо в вершинах
1
2
a
y
)7(
14
a
14
a
1
Рассмотрим вершины.
1
14
Отсюда общее решение
1a
2
1.
При
1
x
7
x
0
4
a
y
0
2
a
8
a
9
Значит,
2
a
19
a
8
41
7
a
224
3
224
3
a
a
Решение
3,224 a
2. При
1x
и
7x
x
0
4
a
y
0
2
a
8
a
9
Значит,
a
3
a
2
либо
8
a
a
19
3
a
4
3
6
a
либо
4
a
3
6
Решение
a
4,3
6
Собирая все решения, получим
a
1
2
4,
6
Ответ:
a
1
2
4,
6
Тригонометрические уравнения и неравенства с параметром.
Задача 19. Найти наибольшее целое a , при котором уравнение
2
cos
sin4
12
3
a
3
4
9
3
a
x
x
x
x
x
2
2
2
2
имеет ровно два различных решения.
1
ax
2
Решение. Выделим полные квадраты:
2
(
x
)2
2
)2
(3
a
)1
sin4
(3
x
2
(
a
)1
cos
(
x
2
)1
(
a
)2
Отсюда
2 (
x
2
)2
(
a
)1
4
3
sin
(
x
2
)2
(
a
)1
2
(
x
2
)1
cos
Обозначим
y
x
(
2
)2
(
a
)1
, тогда получим
y
2
4
3
(
a
)2
sin
y
2
cos
(
x
2
)1
2
(
a
)2
Обозначим
A
cos
(
x
2
)1
2
(
a
)2
, тогда
1
A
1
.
Будем считать, что ищется решение уравнения
y
Строим два графика
)(
yz
y
и
)(
yz
4
A
3
sin
sin
y
2
.
4
A
3
y
2
4
3
4
3
0y
.
Видно, что точка пересечения одна,
Отсюда
0D
. Получаем, что
)2
x
y
(
2
и это уравнение должно иметь два разных корня, то есть
a
0
)1
(
D
a
4
13
. Наименьшее целое
1
0
a
a
0a
Ответ:
cos
0a
не имеет
x
Задача 20. Найти те значения a , при которых уравнение
корней
Решение.
sin3
x
a
4
sin3
x
4
cos
x
a
5
sin
x
Значит,
5
sin3
x
x
5
3
5
cos
4
x
cos
4
5
. При
a
5
cos(
x
)
a
5a
решений не будет.
Задача 21. Найти те значения a , при которых уравнение
не имеет решений.
Решение.
Преобразуем к виду
0
2
x
(cos
83 a
. Значит, если
3
8
(cos
a
)3
cos
cos
)3
2
x
x
x
2
2
Ответ:
x
2
3
3
cos
cos
2
a
x
5a
03 a
или
Ответ:
, решений не будет.
(
)3,
)
,5(
Задачи на применение производной.
Задача 22. Найти те значения a , при которых уравнение
sin
x
cos
x
a
имеет решение.
Решение.
sin x
0
и
cos x
0
, значит, область определения
,0
2
(плюс период).
Найдем наибольшее и наименьшее значения
Это и будут нужные значения a .
cos
sin
x
)(
xy
x
cos
cos
x
cos
x
sin
x
2
2
x
cos
x
xy
)(
sin
x
cos
x
на
,0
2
sin
sin
x
x
sin
x
0
Отсюда
sin
3
x
cos
1)0( y
1
2
4
y
2
y
3
x
tgx
1
x
4
2
сn
учетом
области
определени
.
я
2
2
2
2
4
2
4
8
Ответ:
4 8,1a
2
Задача 23. Найти те значения a , при которых система уравнений
log
имеет ровно два решения.
(
x
)2
3
x
y
x
3
2
ya
x
2
4
2
Решение.
Система сводится к уравнению
Рассмотрим
1
1
a
a
2
log
a
4
y
ya .
2
Строим оба графика:
0
a
)0,1(
)1,0(
0y
0y
a
,1
a
1
Корень
0y единственный. Подставим во второе уравнение:
x
2
3
x
2
y
0
0 y
41
Дискриминант
иметь ровно два решения.
D
0
0
так как
0 y
0
. Значит, при
a
1
a
0
система будет
2
a
1
Рассмотрим
В этом случае график логарифма будет или касаться, или пересекать в двух точках второй
график. В случае касания система тоже будет иметь два решения.
1
a
В точке касания должны совпадать значения функций и их производные:
xf
)(
xg
)(
f
)(
)(
xg
x
4
y
Получаем систему:
4
y
y
3
2
a
2
log
1
ln
a
a
2
1
ln4
2
a
1
ln2
2
a
1
ln2
2
a
2
a
2
ln
a
a
y
log
2
a
a
1
ln8
a
a
1
a
ln
4
y
1
ln4
2
a
подставим
в
первое
log
2
a
y
1
ln4
2
a
Логарифмируем:
log
2
a
a
log
a
2
a
a
1
ln2
1
ln8
a
ln
2
a
1
ln2
2
a
2
ln
a
2
log
a
log
2
a
a
1
ln2
2
a
4
y
2
ln
a
2
a
2
a
1
ln8
a
e
1
2
y
1
ln4
a
1
ln
a
ln
a
ln8ln
Отсюда
a
exp
1
e
8
При таком a происходит касание. Ответ:
a
)0,1(
)1,0(
a
exp
1
e
8
и
Задача 24. Найти те значения a , при которых система уравнений
Просто задача.
z
(
x
cos(
x
2
x
)
y
(
y
sin
ay
Решение.
2(
2
)1
2
z
)
)
sin(
x
xy
2
z
a
1(
1ln(
a
)
)
2
y
x
xy
1)
z
0
имеет единственное решение.
Выделим полный квадрат во втором уравнении:
a
Если поменять местами x и y , то уравнение не изменится, значит, если
решение, то
x .
y
Подставим в первое уравнение:
тоже решение. Чтобы было единственное решение, должно быть
1
,(
yx
),(
xy
2(0
2sin)
cos
2sin
)1
)1
0
x
x
x
x
y
x
)
z
z
z
(
(
2
2
2
2
n
2
.
1
0
x
xy
0 y
Из третьего уравнения
Значит,
Подставим в третье уравнение:
Если
Если
, то из второго следует, что
0
0a
x
sin
n
a
z
sin 2
0
x
z
2
Подставим во второе уравнение:
. Пусто.
1
1
2
x
0
x
1
при
n
0
x
0
. 2
z
a
1
2
n
2
a
1
2
n
именно,
x
0
y
z
1
a
2
Единственное решение будет при
1a
, а
Ответ: при
1a
решение
)0,0,0(
Конспект урока по алгебре в 11 классе, на тему: "Графический способ решения уравнений, неравенств, систем уравнений и систем неравенств".
Конспект урока по алгебре в 11 классе, на тему: "Графический способ решения уравнений, неравенств, систем уравнений и систем неравенств".
Конспект урока по алгебре в 11 классе, на тему: "Графический способ решения уравнений, неравенств, систем уравнений и систем неравенств".
Конспект урока по алгебре в 11 классе, на тему: "Графический способ решения уравнений, неравенств, систем уравнений и систем неравенств".
Конспект урока по алгебре в 11 классе, на тему: "Графический способ решения уравнений, неравенств, систем уравнений и систем неравенств".
Конспект урока по алгебре в 11 классе, на тему: "Графический способ решения уравнений, неравенств, систем уравнений и систем неравенств".
Конспект урока по алгебре в 11 классе, на тему: "Графический способ решения уравнений, неравенств, систем уравнений и систем неравенств".
Конспект урока по алгебре в 11 классе, на тему: "Графический способ решения уравнений, неравенств, систем уравнений и систем неравенств".
Конспект урока по алгебре в 11 классе, на тему: "Графический способ решения уравнений, неравенств, систем уравнений и систем неравенств".
Конспект урока по алгебре в 11 классе, на тему: "Графический способ решения уравнений, неравенств, систем уравнений и систем неравенств".
Конспект урока по алгебре в 11 классе, на тему: "Графический способ решения уравнений, неравенств, систем уравнений и систем неравенств".
Конспект урока по алгебре в 11 классе, на тему: "Графический способ решения уравнений, неравенств, систем уравнений и систем неравенств".
Конспект урока по алгебре в 11 классе, на тему: "Графический способ решения уравнений, неравенств, систем уравнений и систем неравенств".
Конспект урока по алгебре в 11 классе, на тему: "Графический способ решения уравнений, неравенств, систем уравнений и систем неравенств".
Конспект урока по алгебре в 11 классе, на тему: "Графический способ решения уравнений, неравенств, систем уравнений и систем неравенств".
Конспект урока по алгебре в 11 классе, на тему: "Графический способ решения уравнений, неравенств, систем уравнений и систем неравенств".
Конспект урока по алгебре в 11 классе, на тему: "Графический способ решения уравнений, неравенств, систем уравнений и систем неравенств".
Конспект урока по алгебре в 11 классе, на тему: "Графический способ решения уравнений, неравенств, систем уравнений и систем неравенств".
Конспект урока по алгебре в 11 классе, на тему: "Графический способ решения уравнений, неравенств, систем уравнений и систем неравенств".
Материалы на данной страницы взяты из открытых истончиков либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
24.03.2018
Посмотрите также:
© ООО «Знанио»
С вами с 2009 года.
О портале
