
Настоящее пособие предназначено для студентов I курса любых специальностей в объеме 161 часа.
Данный конспект содержит необходимый материал по десяти темам курса математики. изложение теоретического материала по всем темам сопровождается рассмотрением большого количества примеров и задач, ведется на доступном, по возможности строгом языке.
Пособие может быть использовано студентами для самостоятельного изучения соответствующего материала, является базой для подготовки к экзаменам. кроме того, пособие может помочь студенту и в тех случаях, когда он что-то не успел записать на занятии, какие-то занятия были пропущены, в чем-то трудно (или нет времени) разобраться по другим пособиям, учебникам, когда некоторые вопросы «слишком длинны» в его конспектах или много фактического материала, который следует изучить за ограниченное количество времени.
Автор надеется, что данное пособие будет способствовать более глубокому изучению материала студентами колледжа.
Список обозначений:
![]()
![]() – начало и конец решения примера, задачи
– начало и конец решения примера, задачи
![]()
![]() – начало и конец доказательства
– начало и конец доказательства
![]() – важные определения
– важные определения
![]() – обратите особое внимание
– обратите особое внимание
В рамку заключены формулы, которые важно помнить.
Домашние задания сдаются на проверку с соответствующей защитой по графику, который находится при кабинете математики.
Консультации по математике проводятся по расписанию, находящемуся также в кабинете.
Приложения:
В результате изучения темы студенты должны знать:
В результате изучения темы студенты должны уметь:
§ Выполнить с заданной точностью на инженерном или программируемом микрокалькуляторе (в режиме вычислений) арифметические действия;
§ Вычислять значения элементарных функций;
§ Выполнять действия над алгебраическими дробями;
§ Решать уравнения с одной переменной первой и второй степени, биквадратных, иррациональных и др.
§ Выполнять арифметические действия над комплексными числами в алгебраической форме;
§ Решать квадратные уравнения с отрицательным дискриминантом;
§ Решать линейные и квадратные неравенства с одной переменной, системы линейных неравенств;
§ Решать системы линейных и нелинейных уравнений.
1) Роль математики в подготовке специалистов среднего профессионального образования.
2) Современная электронно-вычислительная техника и области ее применения.
3) Понятие о математическом моделировании.
4) Множество действительных чисел. Приближения действительных чисел конечными десятичными дробями.
5) Числовая прямая. Промежутки. Окрестности точки.
6) Простейшие вычисления с помощью МК.
7) Формулы сокращенного умножения.
Числа 1, 2, 3, 4, …… - множество натуральных чисел (N)
Числа ![]() , ……. - множество целых
чисел (Z)
, ……. - множество целых
чисел (Z)
Числа ![]() -
множество рациональных чисел (Q)
-
множество рациональных чисел (Q)
Любое рациональное число можно
записать в виде дроби ![]() , где m
, где m ![]() Z , n
Z , n ![]() N
N
![]()
![]()
![]()
![]() и т.д.
и т.д.
Разделив "m" на "n" получаем конечную или бесконечную десятичную дробь
![]()
![]()
Как видим, у некоторых дробей десятичные знаки повторяются
0,5555 ……; 0,3333 ……; 4,5222 …….;
Такие числа называются периодическими десятичными дробями и записываются:
4,959595 … = 4, (95) 2,125125125 … = 2, (125)
0,5121212 … = 0,5 (12) 2,13444 … = 2,13 (4)
Каждая бесконечная периодическая дробь представляет собой рациональное число (докажем несколько позже), а пока будем использовать правило записи в виде обыкновенной дроби:
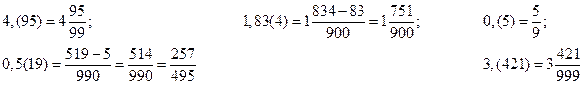
для чисто периодической дроби: в числителе пишется число, стоящее в периоде, а в знаменателе столько "9", сколько цифр в периоде, целая часть остается без изменения.
для смешанной периодической дроби: в числителе разность между числом, стоящим после запятой, и числом, стоящим после запятой до периода, а в знаменателе столько "9", сколько цифр в периоде, со столькими "0", сколько цифр после запятой до периода
Запишите в виде обыкновенной дроби:
5,21 (3) 13, (71) 14,72 (24) 0, (4)
0,7 (125) 10, (125)
Числа, представляющие собой бесконечные непериодические десятичные дроби, называются иррациональными:
4,1728 …. 0,1078612 … 13,200941 …
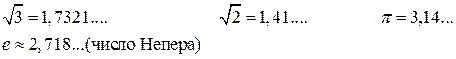
Теорема. Не существует рационального числа, квадрат которого равен числу 2 (предлагается самостоятельно рассмотреть доказательство (автор Яковлев "Алгебра и начала анализа"
ч 1 п 8 (2))
Числа рациональные и иррациональные составляют множество действительных (вещественных) чисел (R). Действительные числа изображаются геометрически на прямой, которая называется осью действительных чисел
|
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
|
||||||||||||||||
Измеряется отрезок, соответствующий числу и откладывается на прямой.
Вы уже знакомы с числовыми множествами, называемыми промежутками. Перечислим их.
Отрезок с концами а и b:
[a;b] = ![]()
Интервал с концами a и b
(a,b) = ![]()
Полуоткрытые промежутки:
(a,b] = ![]() ;
[a,b) =
;
[a,b) = ![]()
Число b - а называется длиной промежутка
Бесконечные промежутки (лучи, полупрямые):
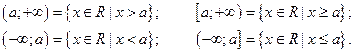
Числовая прямая:
![]() R
R
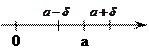 Интервал вида
Интервал вида ![]() называют также
называют также ![]() - окрестностью точки а
- окрестностью точки а
![]() Можно сказать, например, что
все десятичные приближения по недостатку и по избытку к числу
Можно сказать, например, что
все десятичные приближения по недостатку и по избытку к числу ![]() , начиная с третьего (т.е.
приближения
, начиная с третьего (т.е.
приближения ![]() с точностью до 10 - n при
n
с точностью до 10 - n при
n ![]() 3), попадают в
3), попадают в ![]() - окрестность точки
- окрестность точки ![]() при
при ![]() =
0,001.
=
0,001.
При выполнении действий над действительными числами используют правила округления числа
4,762 ![]() 4,76
(с точностью до 0,01)
4,76
(с точностью до 0,01)
4,762 ![]() 4,8
(с точностью до 0,1)
4,8
(с точностью до 0,1)
4,762 ![]() 5
(с точностью до целых чисел)
5
(с точностью до целых чисел)
Самостоятельная работа
Действия на МК с учетом правила округления числа (простейшие вычисления)
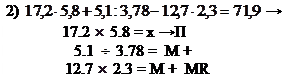 Комбинированные
действия на МК.
Комбинированные
действия на МК.
1) ![]() →
→
2.7 + 3.6 = x →П
4.1 + 5.87 = x MR → П
6.12-3.7 = x MR =
Можно использовать скобки.
3) ![]() =1.342
; 8.39 – 2.492 = X
=1.342
; 8.39 – 2.492 = X![]() M
; 5.13 + 2.784 =
M
; 5.13 + 2.784 =![]() MR
MR
4) ![]() =32.0
13.6 · 0.4 = X
=32.0
13.6 · 0.4 = X![]() M; 0.264 · 29.4
=M+
M; 0.264 · 29.4
=M+
3.07 · 1.56 = /–/ M+ MR![]() 0,266
0,266
Формулы сокращенного умножения
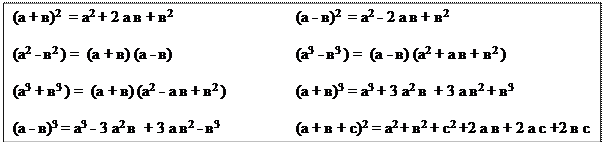
Выполнить действия (самостоятельно)
1. ( 4а + 3с )2 2. ( х3 - 2у + 3ху )2 3. ( 2х - 3у2 - х3у )2
4. ( х2 - 3у ) ( х2 + 3у ) 5. ( х + 2у ) (х2 - 2ху + 4у2 )
Контрольные вопросы
1. Всякая ли обыкновенная дробь - число рациональное?
2. Может ли быть рациональное число отрицательным?
3. Почему бесконечную периодическую десятичную дробь считают рациональным числом?
4. Назовите числа рациональные, иррациональные
2,75354276; 5,
3 (71); ![]()
15,171 171 171 …;
4, 36 (5); ![]() ;
; ![]()
0, 36 78 ..; 1,276 ..;
5. Какие числа, кроме рациональных и иррациональных являются действительными?
6. Можно ли утверждать, что квадратный корень из любого натурального числа есть число иррациональное?
7. Можно ли утверждать, что квадратный корень из любого нечетного числа есть число иррациональное?
1) Мнимая единица. Степень мнимой единицы.
2) Множество комплексных чисел, их геометрическая интерпретация
3) Модуль и аргумент комплексного числа.
4) Действия над комплексными числами в алгебраической форме (сложение, вычитание, умножение, деление, возведение во вторую и третью степень).
5) Элементарные вычисления с помощью МК.
х2 + 4 = 0 х2 = - 4 во множестве R решений нет
![]()
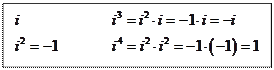
![]() Обозначим:
Обозначим:
Множество действительных чисел и
мнимая единица составляют множество комплексных чисел, тогда ![]()
i 23
= i 3 = - i (23 : 4 = 4 ![]() 5
+ 3)
5
+ 3)
i 23
= i 20 ![]() i 3 = 1
i 3 = 1 ![]() (-i) = - i
(-i) = - i
i 48 = i 0 = 1 i 10 i 8 i 2 = 1 (-1) = -1 i 14 = i 2 = - 1 i 25 = i 1 = i
i 103 = i 3 = - i 2 i 3 - 7 i 8 + 5 i 9 + 4 i 10 = - 2 i - 7 + 5 i - 4 = - 11 + 3 i
Число Z = a + b i - комплексное число (алгебраическая форма записи)
а - действительная часть числа
b i - мнимая часть числа
a
+ b i = a1 + b1 i если а = а1
b = b1
![]()
a + b i
и a - b i называются сопряженными
![]()
Например
2 - 3 i и 2 + 3 i
- 4 - i и - 4 + i , т. е. отличаются знаком перед мнимой частью
Числа a + b i и - a
- b i называются противоположными
![]()
Например
- 3 - 4 i и 3 + 4 i
- 5 + 2 i и 5 - 2 i , т.е. отличаются знаками и перед мнимой и перед действительной частями
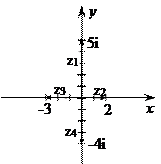
Комплексные числа изображаются геометрически точкой (a; b) или радиусом - вектором, проведенным к этой точке из начала координат
 |
|||
 |
|||
Z 1
= 5i Z 2 = 2 Z 3
= - 3i Z 4 = - 4i
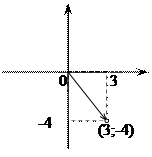
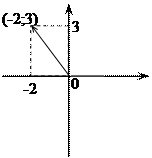
Z = 3 - 4 i Z = - 2 + 3 i
Изобразите числа:
Z = - 7 + 2 i Z = - 9 - i
Z = - 1 - 4 i Z = 12
Z = - 5 i Z = 6 i
Z = - 4 Z = - 3 - 2 i
Итак: a + bi
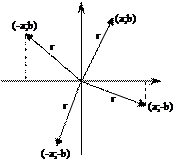 a
a ![]() OX
I ч j > 0 острый
OX
I ч j > 0 острый
b ![]() OY
II ч j >
0 тупой j = 180 0 - j1
OY
II ч j >
0 тупой j = 180 0 - j1
III ч j < 0; тупой j = - (180 0 - j1)
IV ч j < 0; острый
![]() –
модуль комплексного числа
–
модуль комплексного числа
![]() аргумент
комплексного числа
аргумент
комплексного числа
Найти модуль и аргумент комплексного числа:
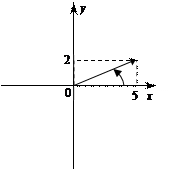 а) Z = 5 + 2 i
а) Z = 5 + 2 i
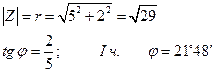
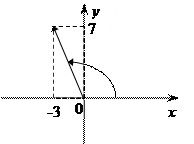 б) Z = - 3 +
7 i
б) Z = - 3 +
7 i
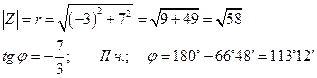
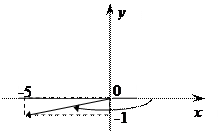
в) Z = - 5 - i
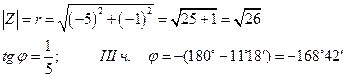
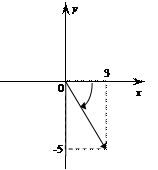
г) Z = 3 - 5 i
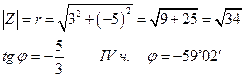
Для чисел, состоящих только из
мнимой или только действительной частей нахождение ![]() и
и
![]() упрощается:
упрощается:
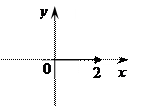 1) Z = 2
1) Z = 2
2 = 2 + 0i Число находится на "ОХ"
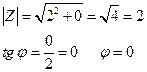

2) Z = 3i
3i = 0 + 3i Число находится на "ОУ"
![]()
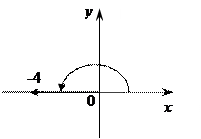
3) Z = - 4
![]() Число
находится на "ОХ" (влево)
Число
находится на "ОХ" (влево)
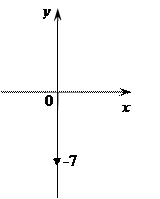 4) Z = - 7 i
4) Z = - 7 i
![]() Число
находится на "ОУ" (вниз)
Число
находится на "ОУ" (вниз)
Самостоятельно
Найти модуль и аргумент комплексного числа
1. Z = - 4 + 3 I 3. Z = - 3 - 7 I 5. Z = - 7 I 7. Z = 3 i
2. Z = - 2 - 5 I 4. Z = 5 + I 6. Z = 2 8. Z = - 4
Z 1 = a 1 + b 1 i
Пусть даны числа: Z 2 = a 2 + b 2 i
Рассмотрим действия над числами
Сложение
Z 1 + Z 2 = (a 1 + b 1 i) + (a 2 + b 2 i) = a 1 + b 1 i + a 2 + b 2 i = (a 1 + a 2) + (b 1 + b 2) i
Вычитание
Z 1 - Z 2 = (a 1 + b 1 i) - (a 2 + b 2 i) = a 1 + b 1 i - a 2 - b 2 i = (a 1 - a 2) + (b 1 - b 2) i
Умножение
Z 1![]() Z 2 = (a 1 +
b 1 i)
Z 2 = (a 1 +
b 1 i)![]() (a 2 + b 2
i) = a 1
(a 2 + b 2
i) = a 1 ![]() a 2
+ b 1
a 2
+ b 1![]() а 2 i + a 1
а 2 i + a 1![]() b 2 i + b 1
b 2 i + b 1![]() b 2 i 2 =
b 2 i 2 =
= a 1 ![]() a 2 + i (b 1
a 2 + i (b 1![]() а 2 + a 1
а 2 + a 1![]() b
2) - b 1
b
2) - b 1![]() b 2 =
(a 1
b 2 =
(a 1 ![]() a 2 - b
1
a 2 - b
1![]() b 2) + (b 1
b 2) + (b 1![]() а 2 + a 1
а 2 + a 1![]() b
2) i
b
2) i
Например
1) (3 - 5
i)![]() (- 3 + i) = - 9 + 15 i + 3 i - 5 i 2
= - 9 +18 i + 5 = - 4 + 18i;
(- 3 + i) = - 9 + 15 i + 3 i - 5 i 2
= - 9 +18 i + 5 = - 4 + 18i;
т.к. i 2 = - 1, то -5![]() (-1) = 5
(-1) = 5
2) (2 - 3 i)![]() (2 + 3 i) = 4 - 9 i 2 =
4 + 9 = 13
(2 + 3 i) = 4 - 9 i 2 =
4 + 9 = 13
( a + b i )![]() ( a - b i ) = a 2 - b 2
i 2 = a 2 + b 2
( a - b i ) = a 2 - b 2
i 2 = a 2 + b 2
![]()
Сумма квадратов
Сумма квадратов разлагается на множители только во множестве комплексных чисел
Деление
![]()
конкретно на примере:
![]()
Возведение в квадрат, куб (используем формулы сокращенного умножения)
Z = ( a + b i ) 2 = a 2 + 2 a b i + b 2 i 2 = a 2 + 2 a b i - b 2;
например:
1) ( - 4 + i ) 2 = 16 - 8 i + i 2 = 16 - 8 i - 1 = 15 - 8 i
2) ( 2 - 3
i ) 3 = 8 - 3![]() 22
22![]() 3 i + 3
3 i + 3![]() 2
2![]() ( - 3 i ) 2 - 27 i 3
= 8 - 36 i + 54 i 2 - 27 i 3 =
( - 3 i ) 2 - 27 i 3
= 8 - 36 i + 54 i 2 - 27 i 3 =
= 8 - 36 i - 54 + 27 i = - 46 - 9 i
Выполнить действия
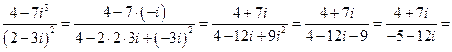
при этих действиях использованы правила: i 3 = - i; i 2 = - 1; ( a - b ) 2 = a 2 - 2 a b + b 2 , а теперь разделим, для этого умножим знаменатель на сопряженное ему число ( - 5 + 12 i) , а чтобы дробь не изменилась умножаем и числитель на это число, т.е.
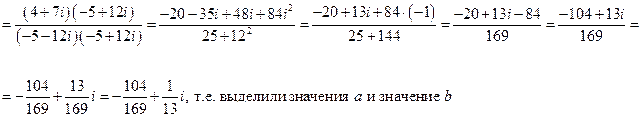
Самостоятельно
Выполнить действия
![]()
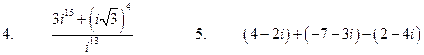
![]()
Контрольные вопросы
1. Что принято за мнимую единицу?
2.
Чему равно ![]()
3. Какое число называется комплексным числом?
4. Какие комплексные числа называются сопряженными, противоположными?
5. Как найти i в любой степени?
6. Как изображается геометрически комплексное число?
7. Чему равен модуль комплексного числа?
8. Как находится аргумент комплексного числа?
9. Как выполняются действия сложение и вычитание комплексных чисел?
10. Как выполняется умножение комплексных чисел?
11. Чему равно произведение двух сопряженных комплексных чисел?
12. Как выполняется деление комплексных чисел?
1) Уравнения I–II степени с одной переменной
2) Неравенства I–II степени с одной переменной
3) Системы неравенств с одной переменной
4) Метод интервалов
5) Вычисления с помощью МК
6) Выдача домашнего задания № 1
![]() – линейное уравнение I степени с одной переменной
– линейное уравнение I степени с одной переменной
![]() – уравнение II степени с одной переменной
– уравнение II степени с одной переменной

Решить уравнение – значит найти множество его корней или доказать, что их нет.
это множество называют решением уравнения.
Два уравнения называются равносильными если решение (корень) одного уравнения является решением (корнем) другого уравнения и наоборот.
Уравнения ![]() равносильны,
так как оба имеют единственный корень
равносильны,
так как оба имеют единственный корень ![]() .
.
Уравнения ![]() и
и ![]() – неравносильны, так как
– неравносильны, так как ![]() является корнем первого уравнения,
но не удовлетворяет второму уравнению.
является корнем первого уравнения,
но не удовлетворяет второму уравнению.
Уравнения ![]() и
и ![]() неравносильны, так как корень
первого уравнения
неравносильны, так как корень
первого уравнения ![]() , а второе уравнение
кроме этого корня имеет еще корень
, а второе уравнение
кроме этого корня имеет еще корень ![]() , который не
является корнем первого уравнения.
, который не
является корнем первого уравнения.
Решим уравнения:
![]()
раскроем скобки, применяя формулы сокращенного умножения ![]() и
и ![]()
![]()
![]()
приведем подобные члены, получим
![]()
![]() Ответ:
Ответ: ![]() – корень уравнения.
– корень уравнения.
![]() разложим
разложим ![]() на множители
на множители
перенесем все члены уравнения в левую часть и приведем дроби к общему знаменателю
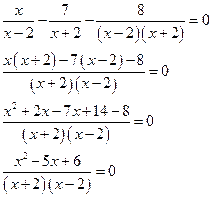
дробь равна нулю, когда её числитель равен нулю, а знаменатель не равен нулю, т. е.
![]()
Решаем уравнение
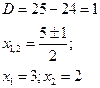 (корни можно найти по
теореме Виета)
(корни можно найти по
теореме Виета)
Так как ![]() – посторонний
корень и решением уравнения будет
– посторонний
корень и решением уравнения будет ![]() . Ответ:
. Ответ: ![]() .
.
![]()
уравнение не имеет действительных корней. Найдем мнимые корни.
![]() (мы знаем, что
(мы знаем, что ![]() – мнимая единица)
– мнимая единица)
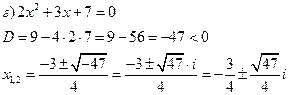
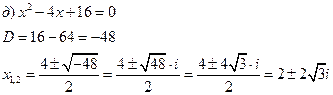
Самостоятельно
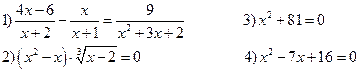
![]() – неравенства
I степени с одной переменной
– неравенства
I степени с одной переменной
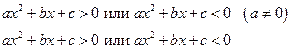 – неравенства II степени с одной переменной
– неравенства II степени с одной переменной
Решить неравенство – значит найти множество значений переменной, при которых это неравенство является верным.
Два неравенства называются равносильными, если множество решений этих неравенств совпадают.
Решим неравенства
а) ![]()
Перенесем все члены в левую часть и приведем к общему знаменателю. общий знаменатель 10; так как знаменатель не содержит переменной, то есть сразу видно что он не равен нулю, то в дальнейшем его можно не писать (опустить).
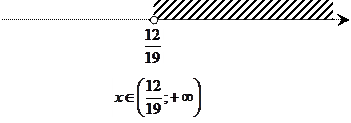
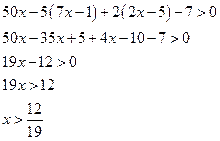
б) ![]()
![]() , то есть
, то есть ![]()
Используя свойства числовых неравенств, имеем
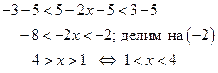 , знак неравенства
меняется на противоположный
, знак неравенства
меняется на противоположный
![]()
Или можно записать в виде системы неравенств
![]()
![]()
в) ![]()
![]()
![]()
Решаем две системы

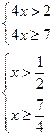
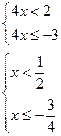
Ответ: ![]() .
.
г) ![]()
умножим на (–1)
![]()
квадратное неравенство
Найдем корни уравнения ![]()
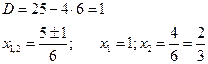
Графиком функции ![]() является
парабола, ветви которой направлены вверх, а точки пересечения параболы и оси OX
является
парабола, ветви которой направлены вверх, а точки пересечения параболы и оси OX ![]()
Изобразим геометрически:

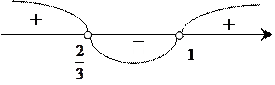
или
или
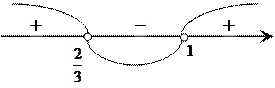 получаем три интервала, в которых определяем знак трехчлена. Так как
мы решаем неравенство
получаем три интервала, в которых определяем знак трехчлена. Так как
мы решаем неравенство ![]() , то решением неравенства
будет промежуток (интервал)
, то решением неравенства
будет промежуток (интервал) ![]()
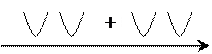 действительных корней нет, так как ветви параболы направлены вверх,
то парабола не пересекает ось и расположена выше её, где всегда > 0,
действительных корней нет, так как ветви параболы направлены вверх,
то парабола не пересекает ось и расположена выше её, где всегда > 0,
а мы решаем неравенство ![]() ,
значит данное неравенство не имеет решения.
,
значит данное неравенство не имеет решения.
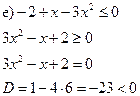
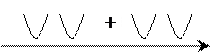 уравнение не имеет действительных корней, т.е. парабола не
пересекает ось, ветви параболы направлены вверх,
уравнение не имеет действительных корней, т.е. парабола не
пересекает ось, ветви параболы направлены вверх,
а так как мы решаем неравенство ![]() ,
то оно имеет множество решений, т.е.
,
то оно имеет множество решений, т.е. ![]() .
.
ж) ![]() – дробно–рациональное неравенство,
которое может быть решено или через системы неравенств или методом интервалов.
Перенесем правую часть в левую, приведем подобные члены
– дробно–рациональное неравенство,
которое может быть решено или через системы неравенств или методом интервалов.
Перенесем правую часть в левую, приведем подобные члены
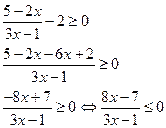
Решим через системы неравенств. Дробь < 0, если числитель и знаменатель имеют разные знаки, т.е.
![]()
(Дробь равна нулю, если числитель равен нулю, а знаменатель не равен нулю).
При решении системы неравенств надо решить каждое неравенство и выбрать общие промежутки.
Решаем 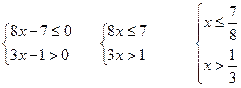

![]()

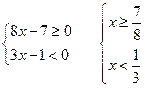
система не имеет решения. Следовательно решением данного
неравенства является ![]() .
.
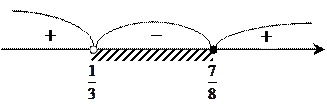
Метод интервалов позволяет ускорить процесс решения
неравенства ![]() корни
корни ![]() и
и
![]() .
.
![]()
Метод интервалов позволяет решать не только неравенства II степени, дробно–рациональные но и более высоких степеней.
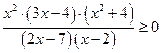 находим корни многочлена
находим корни многочлена
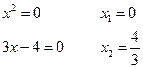
![]() всегда, т.е.
действительных корней нет.
всегда, т.е.
действительных корней нет.
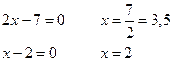
Отметим корни на числовой прямой, учитываем, что числитель может быть равен нулю.
 только определяем знак выражения в каждом промежутке
только определяем знак выражения в каждом промежутке
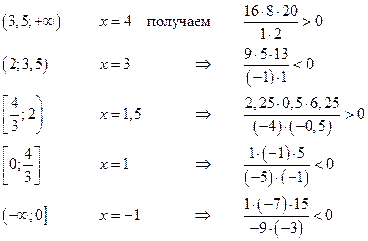
и тогда решением неравенства является ![]() .
.
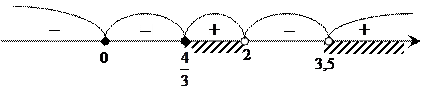 Можно несколько ускорить процесс определения знака в промежутках.
Можно несколько ускорить процесс определения знака в промежутках.
В промежутке больше большего корня всегда выражение больше нуля, а затем, если корень повторяется нечетное число раз (кратность его нечетная), то знаки в промежутках справа и слева от корня изменяются, а если кратность корня четная, то знак справа и слева от корня не изменяется.
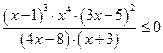
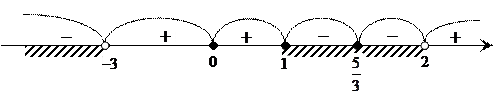
![]() , так как
, так как ![]() , то
, то ![]() можно
записать
можно
записать ![]()
и тогда ![]()
Самостоятельно:
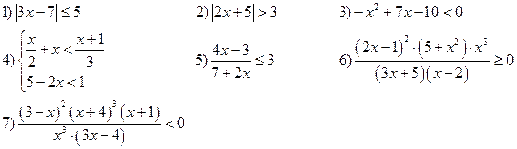
Вычисления с помощью МК:
8) 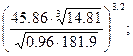 9)
9) ![]() 10)
10) ![]()
11) ![]() 12)
12)
![]()
Выдается домашнее задание № 1 (решение уравнений и неравенств, приложение № 1).
1) Биквадратные уравнения
2) Двучленные уравнения
3) Иррациональные уравнения
4) Вычисления на МК
![]() решается сведением к
квадратному уравнению с помощью введения новой переменной. пусть
решается сведением к
квадратному уравнению с помощью введения новой переменной. пусть ![]() , тогда имеем
, тогда имеем ![]() и решается квадратное уравнение
относительно y.
и решается квадратное уравнение
относительно y.
Например.
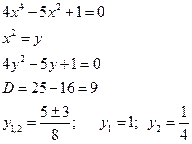
и тогда ![]() , решаем эти
уравнения:
, решаем эти
уравнения:
![]() получили четыре
действительных корня. Ответ:
получили четыре
действительных корня. Ответ: ![]()
Решить самостоятельно:
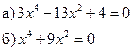
Двучленные уравнения
![]() уравнение третьей
степени и имеет 3 корня. Как их найти? Разложим левую часть уравнения на
множители.
уравнение третьей
степени и имеет 3 корня. Как их найти? Разложим левую часть уравнения на
множители.
Применяем формулу: ![]()
![]()
![]() произведение равно нулю,
если хотя бы один из сомножителей равен нулю, т.е.
произведение равно нулю,
если хотя бы один из сомножителей равен нулю, т.е. ![]()
![]()
![]() действительных корней
нет, найдем мнимые
действительных корней
нет, найдем мнимые
![]() т.е.
уравнение имеет один действительный корень
т.е.
уравнение имеет один действительный корень ![]() и
два мнимых
и
два мнимых ![]()
![]() разложим на множители
разложим на множители ![]() имеем:
имеем:
![]() или
или ![]()
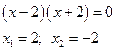
![]() действительных корней нет, введём
мнимую единицу
действительных корней нет, введём
мнимую единицу
![]() есть
два мнимых корня
есть
два мнимых корня
Ответ: ![]() .
.
![]() группируем члены
группируем члены
![]() выносим общий множитель
из каждой скобки
выносим общий множитель
из каждой скобки
![]()
Вынесем ![]() за скобки
за скобки
![]() и тогда
и тогда
![]() или
или ![]()
![]()
![]()
![]() Ответ:
Ответ:
![]() .
.
Самостоятельно:
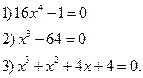
Иррациональные уравнения
Уравнения, содержащие переменную под знаком корня, называются иррациональными. При решении иррациональных уравнений необходимо учитывать:
1) При извлечении корня четной степени берется только арифметическое его значение
2) При возведении выражения, содержащего переменную, в степень может быть нарушена равносильность выражений
Рассмотрим на примерах:
![]()
перенесем x в правую часть
![]()
возведем обе части уравнения в квадрат. Так как ![]() , то получаем
, то получаем
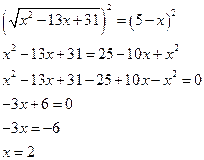
так как при решении уравнения мы возводили в квадрат, то
корень ![]() требует проверки. Итак
требует проверки. Итак ![]() подставляем в данное уравнение
подставляем в данное уравнение
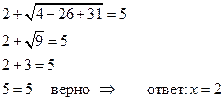
![]()
уравнение содержит два корня, перенесем один из корней в правую часть
![]()
возведем обе части уравнения в квадрат
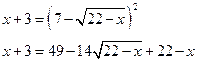
остался один корень. Перенесем его в левую часть, остальные члены – в правую
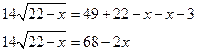
сократим обе части на 2
![]()
и опять возведем в квадрат обе части уравнения:
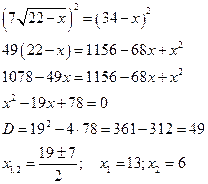
Проверка
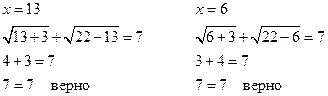
Ответ: x = 13; x = 6.
 Можно было указать сразу ОДЗ и получив корни, сравнить с ОДЗ
Можно было указать сразу ОДЗ и получив корни, сравнить с ОДЗ
![]()
полученные корни x = 13 и x = 6 удовлетворяют
ОДЗ ![]() и следовательно
и следовательно
Ответ: x = 13; x = 6
3) ![]()
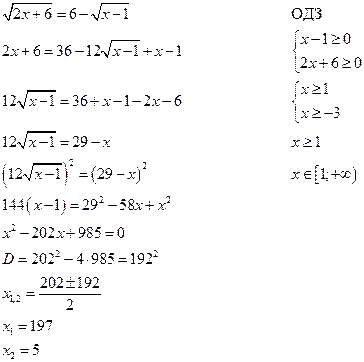
Из того, что ![]() делаем вывод,
что
делаем вывод,
что ![]() и
и ![]() являются
корнями уравнения. Однако проверка показывает, что
являются
корнями уравнения. Однако проверка показывает, что ![]() в
данном случае является посторонним корнем
в
данном случае является посторонним корнем
![]()
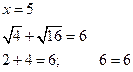 Ответ:
5.
Ответ:
5.
Решить самостоятельно:
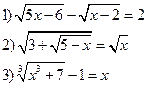
Решим уравнения:
![]()
Отсюда 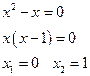 и
и 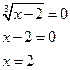
Проверим корни:
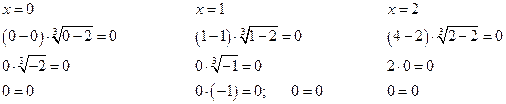
Ответ: 0; 1; 2.
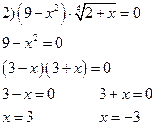 или
или 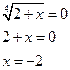 ОДЗ:
ОДЗ: ![]()
Проверяя полученные корни, видим, что ![]() удовлетворяют ОДЗ, а вот
удовлетворяют ОДЗ, а вот ![]() – посторонний корень. Ответ:
– посторонний корень. Ответ: ![]() .
.
Вычислить на МК
Проверить результаты:
1) ![]() = 0,0441 2)
= 0,0441 2) 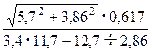 = 0.120
= 0.120
3) ![]() = 2.7
= 2.7![]() 4)
4)
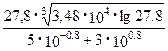 =
52.02
=
52.02
5) ![]() = 6.65
= 6.65
1) Системы двух линейных уравнений с двумя переменными
2) Определитель второго порядка, его вычисление
3) Правило Крамера при решении систем уравнений
4) Свойства определителя второго порядка
5) Вычисления при помощи МК.
в общем виде имеет вид
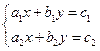
Решением системы уравнений называется упорядоченная пара чисел, удовлетворяющая каждому уравнению этой системы. При решении такой системы могут быть использованы известные методы: 1) подстановки; 2) алгебраического сложения; 3) графически.
Но существует
ещё метод решения, который особенно удобен в том случае, когда коэффициенты ![]() отличны от единицы или содержат
буквенные выражения.
отличны от единицы или содержат
буквенные выражения.
Имеем систему уравнений
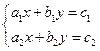
Число 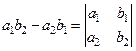 называется определителем второго
порядка. Вертикальные прямые – знак определителя. Обозначается определитель
знаком
называется определителем второго
порядка. Вертикальные прямые – знак определителя. Обозначается определитель
знаком ![]() (дельта).
(дельта).
Итак определитель – это число, которое вычисляется по определенному правилу
![]()
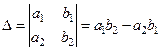
![]() –
первый столбик (коэффициенты при переменной x)
–
первый столбик (коэффициенты при переменной x)
![]() – второй столбик (коэффициенты при
переменной y)
– второй столбик (коэффициенты при
переменной y)
![]() –
первая строчка (коэффициенты при переменных первого уравнения)
–
первая строчка (коэффициенты при переменных первого уравнения)
![]() –
вторая строчка (коэффициенты при переменных второго уравнения)
–
вторая строчка (коэффициенты при переменных второго уравнения)
Определители
при переменных ![]() и
и ![]() получаются из определителя системы
путем замены соответствующего столбика столбиком из свободных членов.
получаются из определителя системы
путем замены соответствующего столбика столбиком из свободных членов.

Для нахождения значений
переменных x и y используются формулы ![]() ,
которые называются формулами Крамера.
,
которые называются формулами Крамера.
Исследуем
1) Если
![]() – система имеет единственное
решение
– система имеет единственное
решение
2) Если
![]() , но
, но ![]() или
или ![]() система не имеет решения
система не имеет решения
3) Если
![]() и
и ![]() и
и ![]() –
система имеет множество решений.
–
система имеет множество решений.
Например ![]()
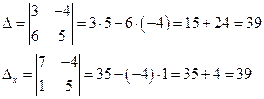
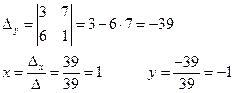 Ответ: (1; –1).
Ответ: (1; –1).
1. Определитель не изменится, если его строки заменить столбцами, и наоборот
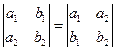
2. При перестановке двух столбцов (строчек) определитель меняет свой знак на противоположный.
3. Определитель, имеющий два одинаковых или пропорциональных столбца (строчки) равен нулю.
4. Общий множитель столбца (строчки) определителя можно вынести за знак определителя.
Рассмотрим примеры:
Решить систему уравнений:
![]()
![]()
![]() система
имеет единственное решение
система
имеет единственное решение
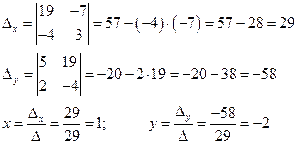 Ответ: (1; –2).
Ответ: (1; –2).
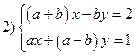
Более рационально систему решить через определитель второго порядка
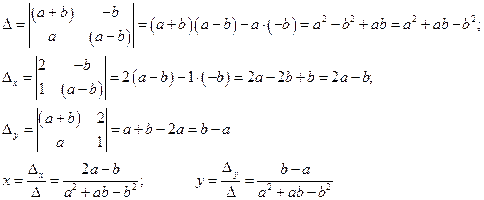
Система имеет единственное решение при условии, что ![]() т.е.
т.е. ![]()
При решении системы двух линейных уравнений с двумя переменными следует помнить, что решение можно выполнить любым из известных методов решения, просто следует выбрать каким методом более рационально для данной системы.
3) ![]()
Решим систему всеми способами, т.е. убедимся, что результат получается одинаковый и определимся, какой из методов более рационально применим для данной системы.
1) Способ подстановки.
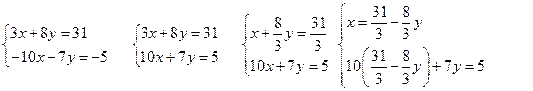
Решаем второе уравнение
относительно «y»: ![]() ,
приведем к общему знаменателю и так как
,
приведем к общему знаменателю и так как ![]() ,
то
,
то
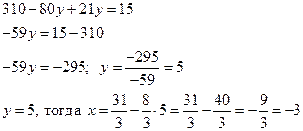 Ответ: x = –3; y = 5.
Ответ: x = –3; y = 5.
2) Способ алгебраического сложения
![]() уравняем по модулю коэффициенты при x,
для этого умножим первое уравнение на 10, а второе – на 3.
уравняем по модулю коэффициенты при x,
для этого умножим первое уравнение на 10, а второе – на 3.
![]()
![]() почленно сложим
почленно сложим
![]()
подставим y = 5 в любое из уравнений системы, например в первое, и найдем x
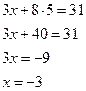
получаем x = –3; y = 5, как и в первом случае.
3) графически (следует помнить, что результаты могут быть получены приближенно, что можно объяснить нашим зрением, умением проводить линии, выбором масштаба, неудобством записи числа и т.д.)
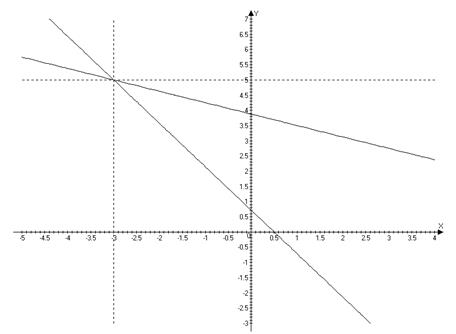
![]() графиком каждого
уравнения является прямая, а прямая определяется двумя точками.
графиком каждого
уравнения является прямая, а прямая определяется двумя точками.
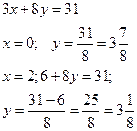
(–3; 5)
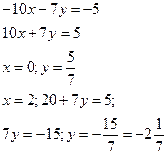
4) C помощью определителя:
![]()
![]()
![]() единственное решение
единственное решение
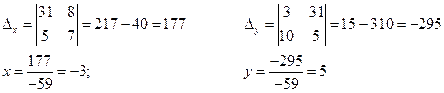
Ответ: (–3; 5).
Каким же способом более рационально можно было решить эту систему? Вы правы, конечно с помощью определителя.
Самостоятельно (любым способом)
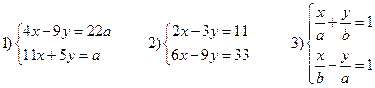
Контрольные вопросы.
1. Что называется определителем II порядка?
2. Как вычисляется определитель II порядка?
3. Какими свойствами обладает определитель?
4.
При каких значениях a система 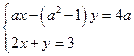 имеет решение, для которого x = 4.
имеет решение, для которого x = 4.
Вычислить при помощи МК.
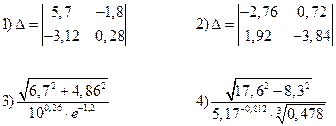
1. Общий вид системы трех линейных уравнений с тремя переменными.
2. Определитель III порядка.
3. Вычисление определителя III порядка.
4. Решение системы трех линейных уравнений с тремя переменными. Правило Крамера.
5. Вычисления при помощи МК.
Система трех линейных уравнений с тремя переменными имеет вид:
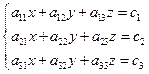
На I курсе рассматривается решение такой системы с помощью определителя третьего порядка.
Выражение, составленное из коэффициентов при
переменных в виде таблицы 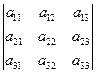 называется
определителем третьего поряда.
называется
определителем третьего поряда.
Определитель третьего порядка вычислить можно через определитель второго порядка или по правилу Саррюса (правило треугольника).
1) Через определитель II порядка.
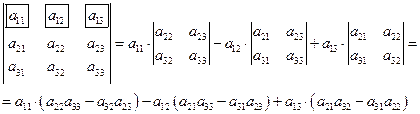
Выделяем ![]() и
мысленно вычеркиваем по столбику и строчке, оставшиеся члены составляют
определитель второго порядка. Берем
и
мысленно вычеркиваем по столбику и строчке, оставшиеся члены составляют
определитель второго порядка. Берем ![]() с
противоположным знаком и вычеркиваем первую строчку и второй столбик,
оставшиеся члены составляют определитель II порядка. Аналогично берем
с
противоположным знаком и вычеркиваем первую строчку и второй столбик,
оставшиеся члены составляют определитель II порядка. Аналогично берем ![]() и
вычеркиваем первую строчку и третий столбик, оставшиеся члены составляют
определитель II порядка.
и
вычеркиваем первую строчку и третий столбик, оставшиеся члены составляют
определитель II порядка.
Выполняем вычисления определителей II порядка по известному уже нам правилу.
Например:
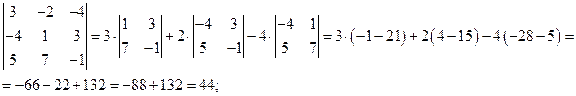
2) Правило треугольника (Саррюса). Рассмотрим схематически
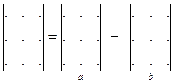 a)
(основания равнобедренных треугольников параллельны главной диагонали)
a)
(основания равнобедренных треугольников параллельны главной диагонали)
b) (основания равнобедренных треугольников параллельны побочной диагонали)
Пример: (возьмем тот же определитель)
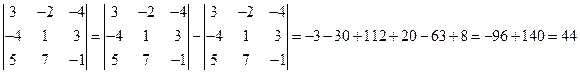
В дальнейшем запись будем вести так
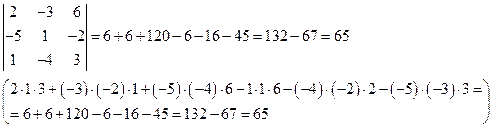
Определители ![]() получаются из
определителя системы путем замены соответствующего столбика столбиком из
свободных членов и вычисляются по тому же правилу, что и определитель системы.
получаются из
определителя системы путем замены соответствующего столбика столбиком из
свободных членов и вычисляются по тому же правилу, что и определитель системы.
Для нахождения значений ![]() пользуются правилами Крамера
пользуются правилами Крамера
![]()
Исследование:
1.
Если ![]() , то система имеет единственное
решение
, то система имеет единственное
решение
2.
Если ![]() , то система несовместима, т.е. не
имеет решения
, то система несовместима, т.е. не
имеет решения
(либо ![]() либо
либо
![]() либо
либо ![]() )
)
3.
Если ![]() , то система неопределенна, т.е.
имеет множество решений
, то система неопределенна, т.е.
имеет множество решений
(![]() и
и
![]() и
и ![]() )
)
Определитель III порядка обладает всеми свойствами определителя II порядка.
Например, решить систему уравнений
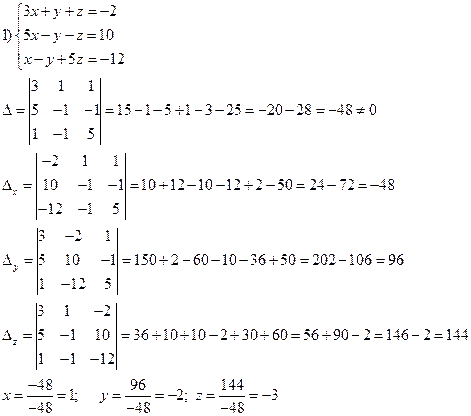
Ответ: (1; –2; –3).
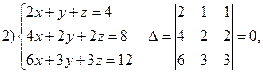
![]() ,
,
так как коэффициенты при переменных и свободные члены
пропорциональны. ![]()
Система имеет множество решений, т.е. неопределена.
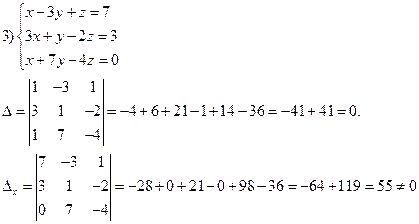
![]() и
и ![]() можно уже не находить.
Следовательно система не имеет решения.
можно уже не находить.
Следовательно система не имеет решения.
Самостоятельно:
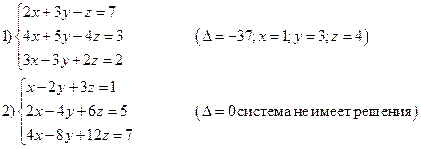
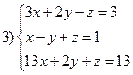
(![]() система имеет множество
решений)
система имеет множество
решений)
Контрольные вопросы:
1) Общий вид системы трех линейных уравнений с тремя переменными.
2) Что называется определителем III порядка?
3) Правила вычисления определителя III порядка (через определитель II порядка, правило треугольника).
4) Свойства определителя III порядка.
5) Формулы (правила) Крамера.
Вычислить при помощи МК:
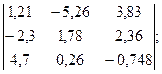
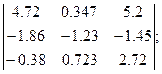
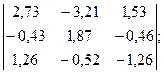
Система уравнений, в которой хотя бы одно из уравнений содержит переменную во второй или выше степени называется нелинейной системой уравнений. Решить систему – значит найти все ее решения. Решением системы называется пара чисел, удовлетворяющая каждому из уравнений системы. Система называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет ни одного решения. Система называется определенной, если она имеет конечное число решений, и неопределенной, если она имеет бесконечное множество решений.
Две системы называются равносильными, если они имеют одно и то же множество решений.
При решении систем нелинейных уравнений наиболее широко используются методы: 1. подстановки; 2. алгебраического сложения; 3. графический; 4. искусственные приемы (применение формул сокращенного умножения, введения новой переменной, использование теоремы Виета и т.д.).
Рассмотрим примеры решения систем уравнений.
1. Решить способом подстановки.
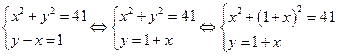
первое уравнение содержит одну переменную, можно выписать это уравнение и решить его.
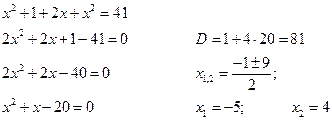
и тогда, подставив полученные значения ![]() и
и ![]() во
второе уравнение, получаем
во
второе уравнение, получаем
![]()
Получаем две пары чисел ![]() ,
которые являются решением данной системы уравнений. Ответ: (5; –4); (4; 5).
,
которые являются решением данной системы уравнений. Ответ: (5; –4); (4; 5).
2. Решить способом алгебраического сложения
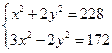
Видим, что каждое из уравнений содержит ![]() , сложим почленно и получаем
уравнение относительно одной переменной.
, сложим почленно и получаем
уравнение относительно одной переменной.
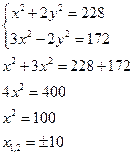
И тогда имеем 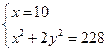 и
и 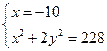 , т.к. системы содержат только
, т.к. системы содержат только ![]() , а
, а ![]() ,
то можно решить только одну из систем и получить значения y
,
то можно решить только одну из систем и получить значения y
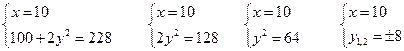
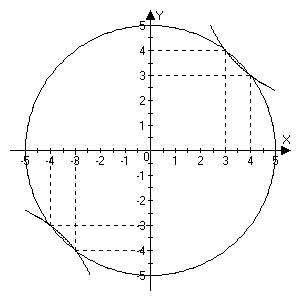 И тогда решением
системы будут
И тогда решением
системы будут ![]() и
и ![]() .
.
3. Решить графически
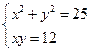
Графическое решение системы уравнений с двумя переменными сводится к отысканию координат общих точек графиков уравнений:
![]() – окружность с центром
(0; 0) и R = 5
– окружность с центром
(0; 0) и R = 5
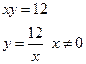 – гипербола
– гипербола
|
x |
2 |
3 |
4 |
6 |
–1 |
–2 |
–3 |
–4 |
–6 |
|
y |
6 |
4 |
3 |
2 |
–12 |
–6 |
–4 |
–3 |
–2 |
Имеем пары чисел (3; 4); (4; 3); (–3; –4); (–4; –3) которые определяют координаты четырех точек.
4. Решить систему уравнений введением новой переменной.
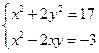 левая часть каждого из уравнений системы есть однородный
(одинаковой степени) многочлен относительно переменных x
и y.
левая часть каждого из уравнений системы есть однородный
(одинаковой степени) многочлен относительно переменных x
и y.
Пусть y = xt
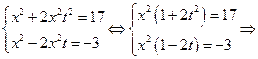
![]() , т.к. тогда и
, т.к. тогда и ![]() , что невозможно.
, что невозможно.
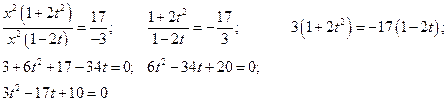
Решаем уравнение относительно t
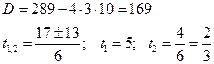
Теперь можно записать системы уравнений
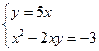 и
и 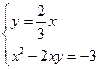
Решаем способом подстановки первую систему:
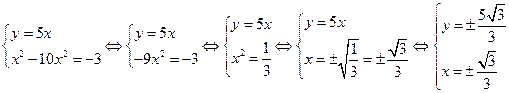
Аналогично решение второй системы:
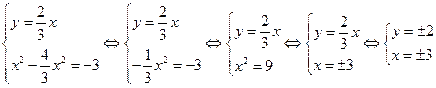
Таким образом получаем пары чисел: 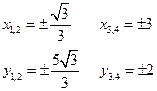
4. 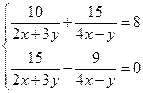
Пусть ![]() и
и ![]() , тогда имеем систему уравнений
, тогда имеем систему уравнений
![]()
Применим способ алгебраического сложения
![]() ,
тогда
,
тогда ![]()
Следовательно имеем систему уравнений
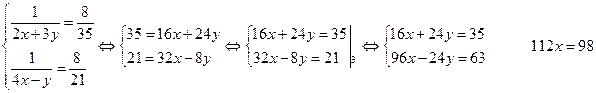
![]() подставив значение
подставив значение ![]() в любое из уравнений системы
в любое из уравнений системы
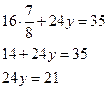
![]() т.е. решением системы
является пара чисел
т.е. решением системы
является пара чисел ![]()
![]()
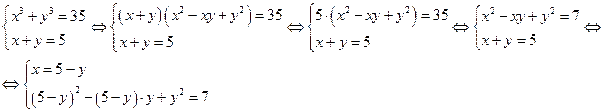
Решаем второе уравнение относительно y;
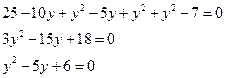 по теореме Виета имеем
по теореме Виета имеем ![]() ,
,
тогда ![]() , т.е. решением
системы будут пары чисел
, т.е. решением
системы будут пары чисел ![]() и
и ![]()
![]()
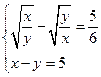
![]() упростим первое уравнение системы
с помощью введения новой переменной
упростим первое уравнение системы
с помощью введения новой переменной
Пусть ![]() , тогда
, тогда ![]() и
уравнение имеет вид
и
уравнение имеет вид ![]() т.к.
т.к. ![]() то
то
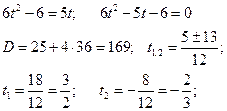
и тогда имеем системы
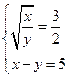 и
и 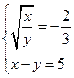
Решаем эти системы относительно x и y
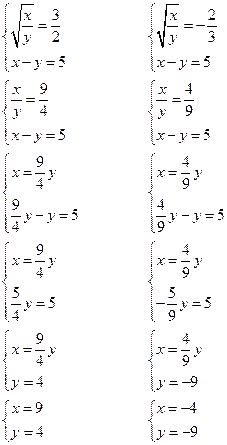
Ответ: (9; 4); (–4; –9).
Замечание. При решении систем нелинейных уравнений предварительно надо решить, каким методом может быть решена система, какие надо выполнить преобразования, какие операции приводят к упрощению систем.
Самостоятельно:
1) 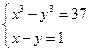 3)
3) 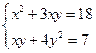
2) 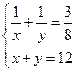 4)
4) ![]()
Вычислить при помощи МК.
1. Собеседование по теоретическим вопросам темы (модуля) (приложение 3).
2. Письменная работа (приложение 4).
3. Выполнение практической работы (практическая работа № 1).
Приложение 1
Вариант I
Решить уравнения: Решить неравенства:
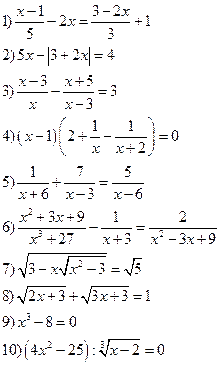
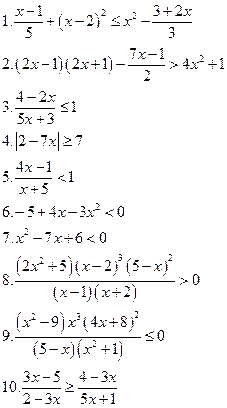
Вариант II
Решить уравнения: Решить неравенства:
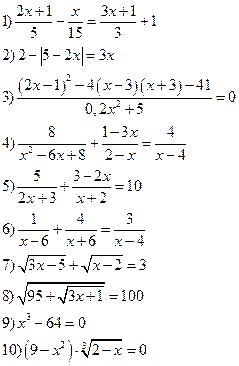
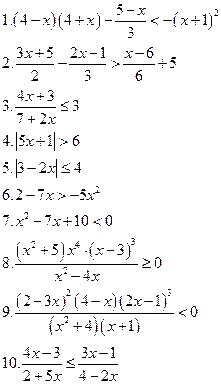
Вариант III
Решить уравнения: Решить неравенства:
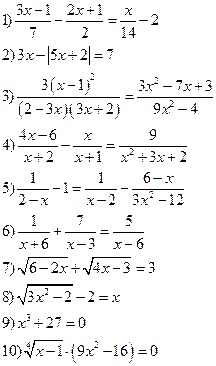
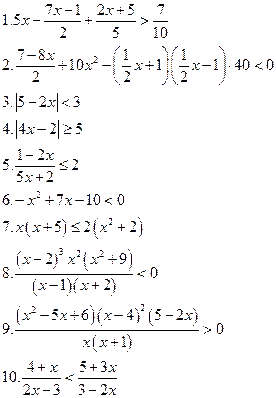
Вариант IV
Решить уравнения: Решить неравенства:
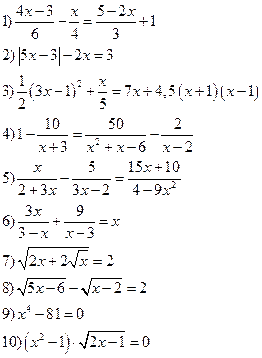
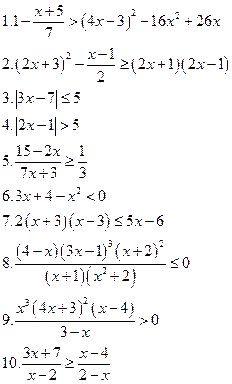
Вариант V
Решить уравнения: Решить неравенства:
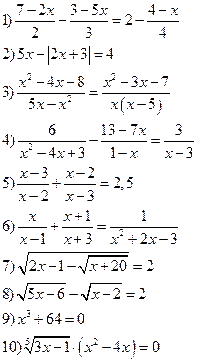
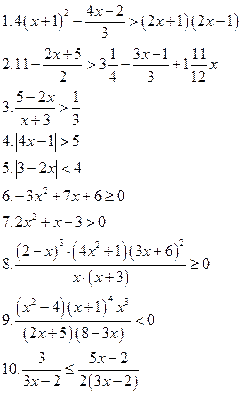
Вариант VI
Решить уравнения: Решить неравенства:
![]()
![]()
Вариант VII
Решить уравнения: Решить неравенства:
![]()
![]()
Вариант VIII
Решить уравнения: Решить неравенства:
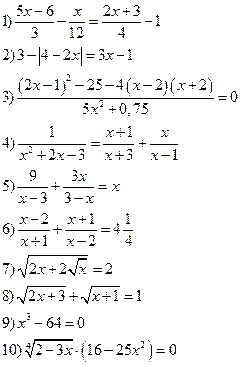
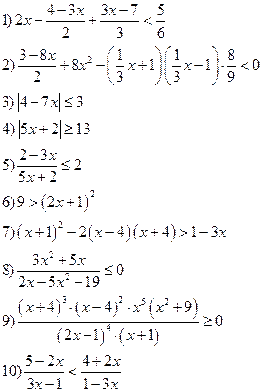
Вариант IX
Решить уравнения: Решить неравенства:
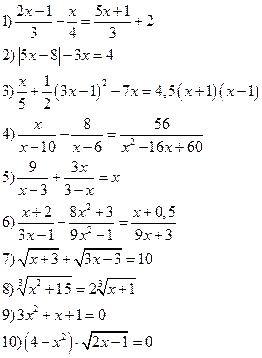
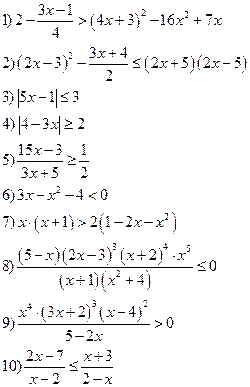
Вариант X
Решить уравнения: Решить неравенства:
![]()
![]()
Приложение 2
Вариант I
Решить системы уравнений:
![]()
![]()
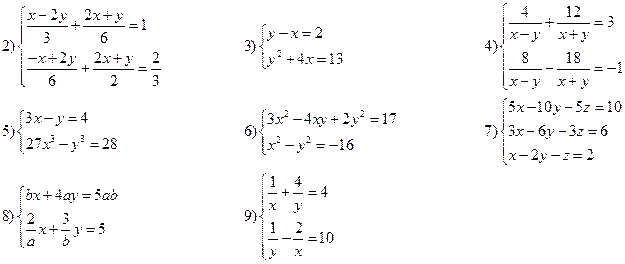
Вариант II
Решить системы уравнений:
![]()
![]()
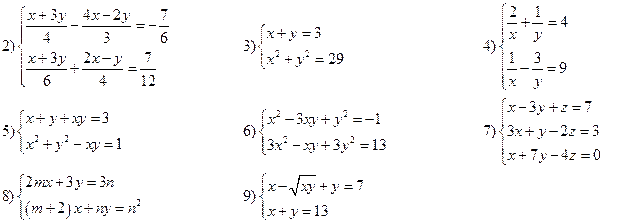
Вариант III
Решить системы уравнений:
![]()
![]()
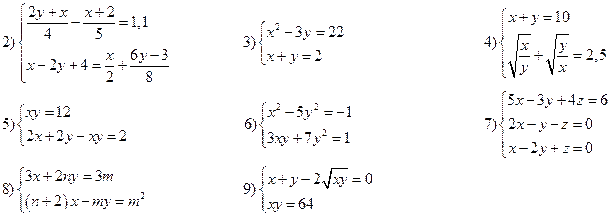
Вариант IV
Решить системы уравнений:
![]()
![]()
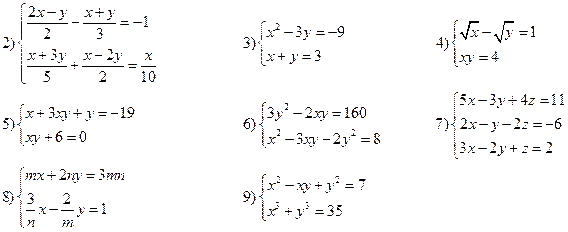
Вариант V
Решить системы уравнений:
![]()
![]()
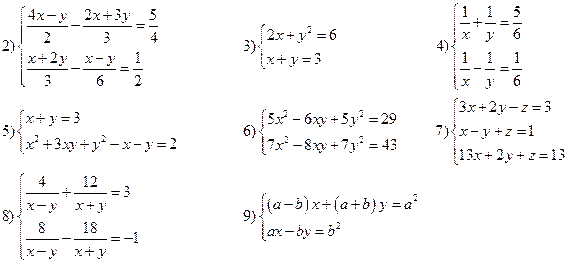
Вариант VI
Решить системы уравнений:
![]()
![]()
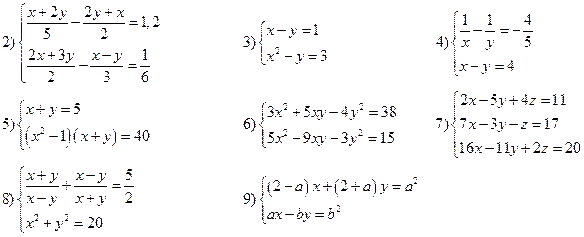
Вариант VII
Решить системы уравнений:
![]()
![]()
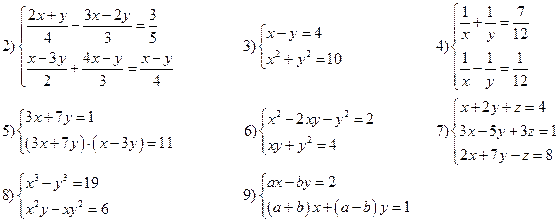
Вариант VIII
Решить системы уравнений:
![]()
![]()
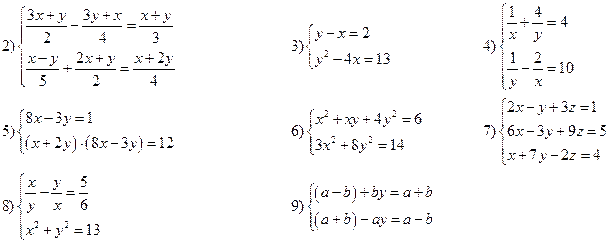
Вариант IX
Решить системы уравнений:
![]()
![]()
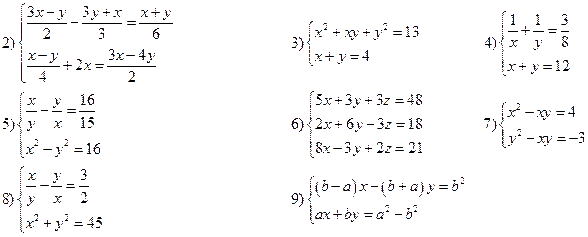
Вариант X
Решить системы уравнений:
![]()
![]()
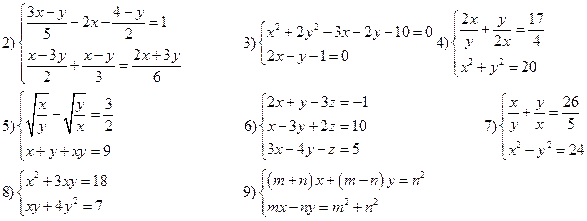
Приложение 3
1) Какие числа называются рациональными?
2) Какие числа называются иррациональными?
3) Какие числа называются действительными?
4) Геометрическое изображение действительных чисел.
5) Правила записи десятичной периодической дроби в виде обыкновенной.
6) Формулы сокращенного умножения.
7) Формула решения квадратного уравнения (дискриминант, нахождение корней уравнения).
8) Формула разложения квадратного трехчлена на множители.
9) Решение биквадратных уравнений.
10) Решение иррациональных уравнений.
11) Решение неравенств с одной переменной. Метод интервалов. (его сущность)
12) Мнимая единица, степень мнимой единицы.
13) Что называется комплексным числом?
14) Какие комплексные числа называются противоположными? сопряженными?
15) Геометрическое изображение комплексных чисел.
16) Модуль комплексного числа, его вычисление.
17) Аргумент комплексного числа, его нахождение.
18) Сложение и вычитание комплексных чисел.
19)
Умножение комплексных чисел в алгебраической форме. Разложение ![]() на множители.
на множители.
20) Деление комплексных чисел в алгебраической форме.
21) Определитель II порядка, его вычисление, свойства.
22) Определитель III порядка, его вычисление, свойства.
23)
Правила нахождения определителей ![]() .
.
24) Правило Крамера при решении систем линейных уравнений.
Приложение 4
1. Решить уравнения: 2. Решить неравенства:
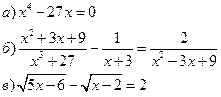
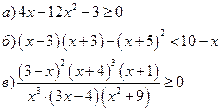
3.Решить системы уравнений: 4. Выполнить действия:
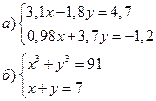
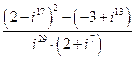
Приложение 5
Практическая работа №1
«Решение уравнений, неравенств, систем уравнений»
I Цель работы: Закрепление навыков решения уравнений и неравенств с одной переменной; систем линейных и нелинейных уравнений.
II Наглядное пособие: МК, карточки заданий.
III Теория.
1) Действительные числа, их геометрическое изображение.
2) Степень числа i
3) Модуль и аргумент комплексного числа, их нахождение.
4) Определитель второго порядка, его вычисление.
5) Определитель третьего порядка, его вычисление.
6) Свойства определителя.
7) Метод интервалов, его применение.
IV Практика (предлагаются задания по карточкам в четырёх вариантах, карточки
прилагаются)
V Контрольные вопросы
1) Как составить определители при переменных?
2) Сущность метода Гаусса, его применения.
3) Почему полученные корни при решении иррационального уравнения требуют проверки или предварительно указать ОДЗ и анализировать принадлежность полученных корней ОДЗ.
4) Какие корни имеет квадратное уравнение при D>0,D=0 и D<0
5) Применение методов интервала при n-ой кратности корней.
6) Укажите, какие из чисел есть числа иррациональные
1,4; ![]() ;
1,5(2);
;
1,5(2); ![]() ; 2,(75); е;
11,96:
; 2,(75); е;
11,96:
IV Литература
1) Яковлев Г.Н. «Алгебра и начало анализа».
2) Богомолов Н.В. « Практические занятия по математике».
3) Справочник по математике(любого автора).
4) Учебники 9-10-11 классов средней школы.
5) Соловейчик И.Л., Лисичкин В.Т. « Математика»
Вариант 1
Решить уравнения, неравенства, системы уравнения.
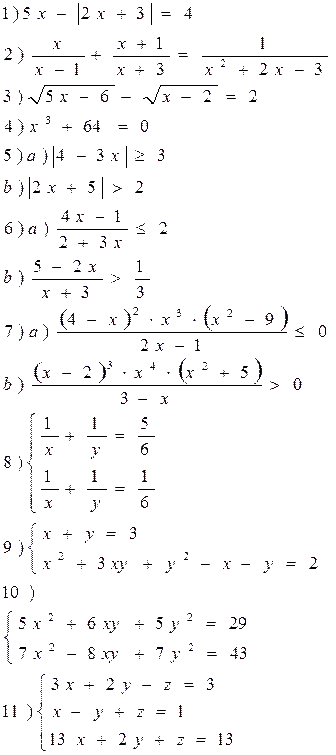
![]()
Вариант 2
Решить уравнения, неравенства, системы уравнения.
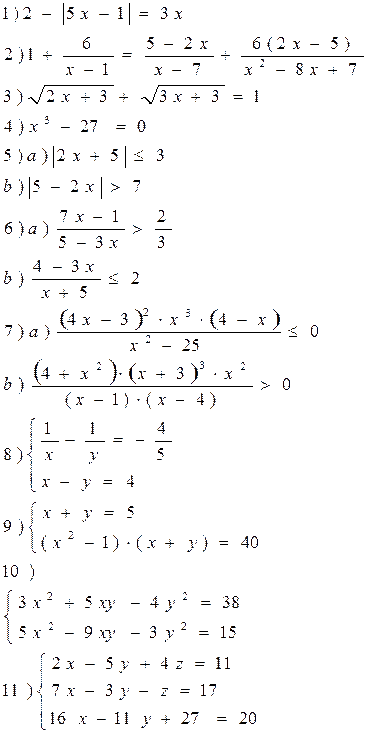
Вариант 3
Решить уравнения, неравенства, системы уравнения.
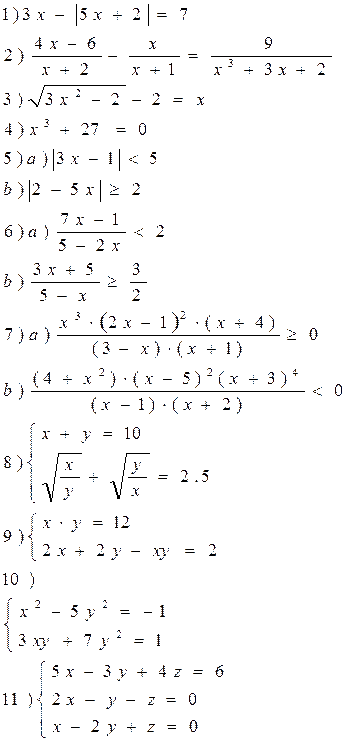
Вариант 4
Решить уравнения, неравенства, системы уравнения.
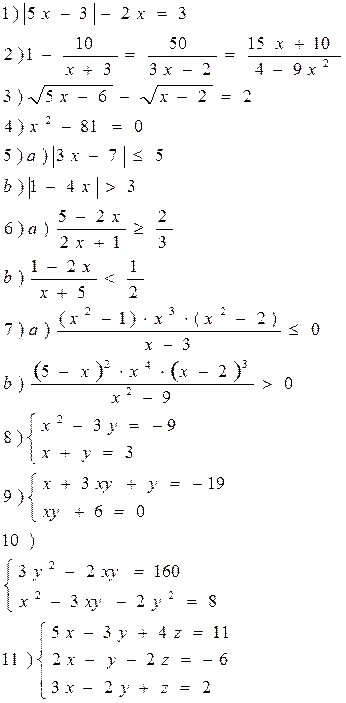
Приложение 6
1. Выполнить действия и результат изобразить геометрически.
1.1 ![]() 1.2
1.2 ![]()
2. Выполнить действия:
2.1 ![]() 2.2
2.2 ![]()
2.3 ![]() 2.4
2.4
![]()
3. Найти модуль и аргумент комплексного числа.
3.1 ![]()
3.2 ![]()
3.3 ![]()
3.4 ![]()
3.5 ![]()
3.6 ![]()
3.7 ![]()
3.8 ![]()
Уравнения с одной переменной.
4. Решить уравнения.
4.1 ![]()
4.3 ![]()
4.2 ![]()
4.4 ![]()
5. Решить биквадратное уравнение.
![]()
6. Решить уравнение методом введения новой переменной.
![]()
7. Сократить дробь:
![]() и вычислить при х = – 2
и вычислить при х = – 2
8. Найти все корни уравнения:
8.1 ![]()
8.2 ![]()
8.3 ![]()
8.4 ![]()
8.5 ![]()
9. Решить иррациональные уравнения.
9.1 ![]()
9.2 ![]()
9.3 ![]()
Неравенства I степени.
10. Решить неравенства:
10.1 ![]()
10.2 ![]()
10.3 ![]()
10.4 ![]()
Неравенства II степени.
11. Решить неравенства:
11.1 ![]()
11.2 ![]()
11.3 ![]()
12. Решить системы неравенств:
12.1 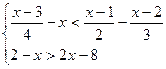
12.2 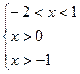
12.3 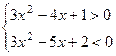
13. Решить неравенство методом интервалов:
13.1 ![]()
13.2 ![]()
13.3 ![]()
13.4 ![]()
13.5 ![]()
Системы уравнений.
14 Решить системы линейных уравнений:
с двумя переменными (всеми способами)
14.1 ![]()
с тремя переменными
14.2 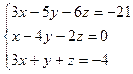 14.3
14.3 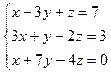
15. Решить системы нелинейных уравнений:
15.1 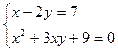
15.2 ![]()
15.3 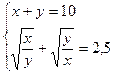
15.4 ![]()
15.5 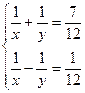
15.6 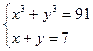
15.7 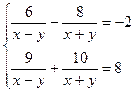
16. Вычислить при помощи МК
16.1 ![]() ;
16.2
;
16.2 ![]() ; 16.3
; 16.3
![]() ;
;
16.4 ![]() ; 16.5
; 16.5 ![]() ;
;
16.6 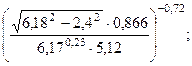 16.7
16.7
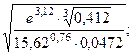 16.8
16.8 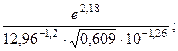
16.9 ![]() 16.10
16.10
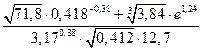
I Основная литература (О.Л.)
1. Яковлев Г. Н. ч. I «Алгебра и начала анализа»
2. Богомолов Н. В. «Практические занятия по математике»
3. Богомолов Н.В., Самойленко П.И. «Математика»
4. Дадаян А.А. «Математика»
II Дополнительная литература (Д.Л.)
III Методические и учебные пособия, изданные в НХК (М.П.)
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.