Научно – практическая работа написана на тему: «Теорема Пифагора».

Абстракт:

    Научно – практическая работа написана на тему: «Теорема Пифагора».

Объектом исследования данной работы являются различные доказательства теоремы Пифагора.

Целью работы является попытка выявить более лёгкое доказательство теоремы Пифагора.

Гипотеза: так как в учебнике «Геометрия 8» дан 10^ый способ доказательства, то он наверное  и является более лёгким.

Этапы исследования:

1.     Работа с литературой.

2.     Нахождение способов поставленной цели.

3.     Обработка результатов.

Работа носила исследовательско - практический характер. Все доказательства были рассмотрены самостоятельно, при этом использовались формулы площади треугольника, квадрата, алгебраические тождества, косинус острого угла, равенство фигур, подобие треугольников.

Работа состоит из исторической справки, одной главы, обоснования, заключения, списка используемой литературы.

           Выбранную тему исследования считаю актуальной, так как из способов     рассмотренных мной, может быть более удобный, чем представлен в учебнике.

1

Аннотация научного проекта, написанного на тему:

«Теорема Пифагора».

Целью исследования стала попытка выявить более лёгкое доказательство теоремы Пифагора.

Новизна исследования в том, что в данной работе рассматриваются всевозможные доказательства теоремы Пифагора: с помощью формулы площади треугольника, квадрата, алгебраические тождества, косинуса острого угла, равенства фигур, подобия.

Ученица, рассмотрела способы доказательства теоремы, проделав предварительную работу по их отбору и классификации.

Проведенные исследования помогают автору приобрести новые знания, умения  и навыки при работе со справочной литературой.

Отмечается хорошее знание автором учебного материала, умение доказывать, делать выводы.

Работа выполнена грамотно с соблюдением всех необходимых требований.

2

Из истории.

Прокл в своём комментарии к «Началам» Евклида пишет относительно предложения о том, что квадрат гипотенузы равен сумме квадратов катетов, следующее: «Если слушать тех, кто любит повторять древние легенды, то придётся сказать, что эта теорема восходит к Пифагору. Рассказывают, что в честь этого открытия он принёс в жертву быка». О том же рассказывает и другой греческий историк древности – Плутарх (I век). На основе этих и других преданий долгое время считали, что до Пифагора эта теорема не была известна и назвали её поэтому «теоремой Пифагора». Это название сохранилось поныне. Однако в настоящее время установлено, что эта важнейшая теорема встречается в вавилонских текстах, написанных за 1200 лет до Пифагора.

О ней писали в своих произведениях римский архитектор и инженер Витрувий, греческий писатель – моралист Плутарх, греческий учёный III века Диоген Лаэрций, математик V века Прокл и многие другие.

Теорема Пифагора издавна широко применялась в разных областях науки, техники и практической жизни.

Одно из древнейших доказательств дано, как полагает Прокл, Евклидом и изложено им в «Началах». Как формулировка, так и доказательство теоремы Пифагора имеют у Евклида чисто геометрический характер.

Землемеры Древнего Египта и Вавилона использовали эту теорему для построения прямого угла. Для этого они бечёвку делили узлами на 12 равных частей и концы связывали. Затем бечёвку растягивали на земле так, что получался треугольник со сторонами 3,4 и 5 делений. Угол треугольника, противолежащий стороне с 5 делениями, был прямой (3²+4²=5²). Поэтому этот треугольник стали называть египетским.

О том, что треугольник со сторонами 3, 4 и 5 есть прямоугольный, знали за 2000 лет до н. э. Египтяне, которые, вероятно, пользовались этим отношением для построения прямых углов при сооружении зданий, в Китае предложение о квадрате гипотенузы было известно по крайней мере за 500 лет до Пифагора, эта теорема была известна и в древней Индии; об этом свидетельствуют следующие предложения, содержащиеся в «Сутрах»:   1) Квадрат диагонали прямоугольника равен сумме квадратов его большей и меньшей стороны.

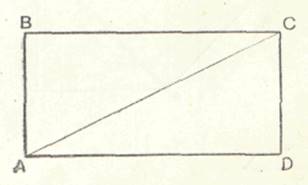
                                                                  Рис 1.

2) Квадрат на диагонали квадрата в два раза больше самого квадрата.

3

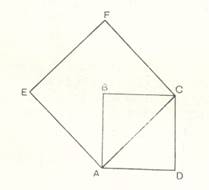
                                                                   Рис 2.

Доказательство теоремы Пифагора считалось в кругах учащихся средних веков очень трудным и называлось иногда Pons Asinorum «ослиный мост» или elefuga – «бегство убогих», так как некоторые «убогие» ученики, не имевшие серьёзной математической подготовки, бежали от геометрии. Слабые ученики, заучившие теоремы наизусть без понимания и прозванные поэтому «ослами», не были в состоянии преодолеть теорему Пифагора, служившую для них вроде непроходимого моста. В связи с чертежом, сопровождающим доказательство Евклида, и другими, ему подобными, теорему Пифагора учащиеся называли также «ветряной мельницей», составляли стишки вроде

«Пифагоровы штаны

во все стороны равны»,

рисовали карикатуры. Одна из них даже появилась в учебнике (рис4).

            Рис 3.                                                                                       Рис 4.

В настоящее время известны более 150 доказательств теоремы Пифагора.                                     

4

Глава 1.

Теорема Пифагора.

Теорема:

     В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов     

     катетов.

1. Одно из старейших наглядных доказательств теоремы Пифагора, содержащееся и в одном из произведений Бхаскары, состоит в следующем:

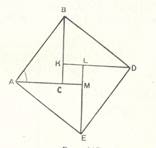
                                                                  Рис 5.

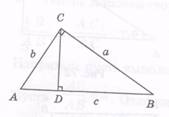
Пусть ABDE – квадрат, сторона которого равна гипотенузе прямоугольного треугольника ABC (AB=c, BC=a, AC=b); далее, пусть DK перпендикулярна к BC, она равна  a; EL^DK, AM^EL; тогда равны треугольники ABC, BDK, DEL и AME. Далее: KL=LM=CM=CK=a – b. Итак, c²=

C²=2ab+b² – 2ab+a²,    откуда    c²=a²+b².

2. Доказательство Евклида:

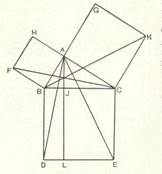
                    Рис 6.                                                                Рис 7.

                                                                            Чертёж к теореме Пифагора

                                                                    в средневековой арабской рукописи.

На гипотенузе и катетах прямоугольного треугольника ВАС он строит соответствующие квадраты и доказывает, что квадрат, построенный на гипотенузе, равновелик сумме квадратов, построенных на катетах следующим образом:

ÐDAC=ÐFBA,  ÐDBC+ÐABC=ÐFBA+ ÐABC;  значит ÐDBA=ÐFBC.

5

Отсюда следует, что треугольники АВС и FBC равны (по двум сторонам и углу между

 ними). Но треугольник ABD равновелик половине прямоугольника BDLI (BD – общее основание, LD – общая высота), а треугольник FBC – половине квадрата HFBA (FB – общее основание, AB – общая высота). Значит, квадрат HFBA равновелик прямоугольнику BDLI. Аналогично доказывается, что квадрат GKCA равновелик прямоугольнику CELI, откуда и следует, что сумма площадей квадратов HFBA и GKCA, построенных на катетах, равна площади квадрата EDBC, построенного на гипотенузе прямоугольного треугольника BAC.

3. Многие из данных после Евклида доказательств теоремы Пифагора основываются на том, что равносоставленные фигуры равновелики: квадраты, построенные на катетах и гипотенузе, разбиваются на многоугольники так, что каждому многоугольнику из состава квадрата на гипотенузе соответствует равный многоугольник одного из квадратов на катетах. В таких случаях достаточно посмотреть на чертёж, чтобы понять всё доказательство, багдадский математик и астроном X века ан-Найризий (Анариций) дал, например, такое доказательство (рис 8)

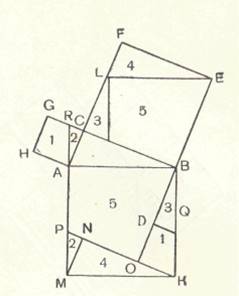
                                                        Рис 8.

4. Другие доказательства основаны на том, что, прибавляя к квадратам на катетах и к квадрату на гипотенузе равные фигуры, получаем равновеликие фигуры. Например, на

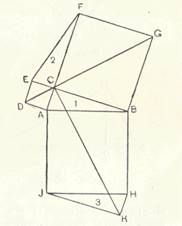
                                                           Рис 9.

6

рис. 9 к Пифагоровой фигуре прибавлены треугольники 2 и 3, равные исходному тре

угольнику 1. Доказательство теоремы Пифагора сводится тут к доказательству равновеликости шестиугольников DABGFE и CAIKHB. Последнее видно из того, что DG делит пополам первый, CK – второй шестиугольник, и если повернуть половину первого шестиугольника DABG вокруг A на 90°, то она совпадёт с CAIK, половиной второго шестиугольника.

5. А вот ещё одно доказательство.

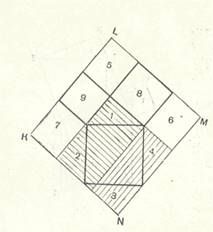
                                                                    Рис 10.

Тут Пифагорова фигура достроена до прямоугольника KLMN. Отнимая многоугольники 1, 2, 3, 4, 5, 6, 7, 8, 9, то получаем квадрат, построенный на гипотенузе, а, отнимая из того же прямоугольника фигуры, равновеликие только что перечисленным (5, 6, 7 и заштрихованные прямоугольники), получаем квадраты 8 и 9, построенные на катетах, и доказываем, что площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов 8 и 9.

6.  В некоторых случаях при доказательствах используют алгебраические тождества. Так, выполнив чертёж

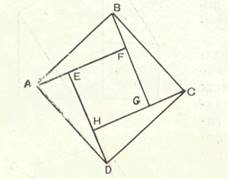
                                                                  Рис 11.

и записав площадь квадрата через его элементы, квадрат гипотенузы  выразится через сумму квадратов катетов треугольника (док 1).

7. Немало доказательств теоремы Пифагора основано на теории подобия. В XIX – XX веках, идя по следам Лежандра, большинство авторов школьных учебников применяют арифметику и алгебру в изложении элементарной геометрии. Так, например, в «Элемен

7

тарной геометрии» профессора А. Ю. Давидова изложено следующее доказательство.

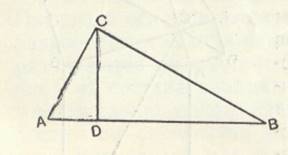
                                                                     Рис 12.

Из подобия треугольников ACD и CAB следует:    ,    или   AC²=AB●AD  (1)

Из подобия же треугольников ABC и DCB следует:   ,   или BC²=AB●BD.    (2)

Сложив почленно равенства 1 и 2, получим:                   AC²+BC²=AB².

 Это доказательство, излагаемое нередко и в современных учебниках, берёт своё начало у Бхаскары (XII век), оно находится и в «Практической геометрии» Леонардо Фибоначчи и у Валлиса (XVII век).

8. В учебнике «Геометрия 7-9» под редакцией Л.С.Атанасяна дано следующее доказательство:

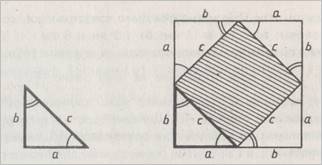
                                                   а)             Рис13               б)

Достроим треугольник рис 13а до квадрата со стороной a+c так, как показано на рисунке 13б. Площадь S этого квадрата равна (a+b)². С другой стороны, этот квадрат составлен из четырёх равных прямоугольных треугольников, площадь каждого из которых равна ab, и квадрата со стороной c, поэтому S=4●ab+c².

Таким образом, (a+b)²=2ab+c², откуда c²=a²+b².

Теорема доказана.

10.В учебнике «Алгебра 8» под редакцией А.Н.Шыныбекова дано доказательство, которое могли бы использовать древни индусы (рис14).

8

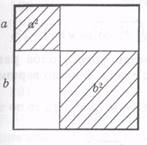
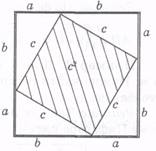
                                                  a              b

                                            а)                       Рис14                    б)

На этих рисунках площади заштрихованных фигур равны между собой. Если на рис. 14а площадь заштрихованной фигуры равна a²+b², то на рисунке 14б эта площадь равна c². Следовательно, c²=a²+b².Здесь a и b – катеты, а c – гипотенуза прямоугольного треугольника.

10. В учебнике «Геометрия 8» под редакцией А.Н.Шыныбекова и «Геометрия 7-11» под редакцией А.В. Погорелова дано ещё одно доказательство

                                                                      Рис15

 Проведём высоту из вершины прямого угла C прямоугольного треугольника ABC. По определению косинуса угла cos(ÐA)=_.   Из прямоугольного треугольника ACD получим равенство cos.(ÐA)= .Отсюда получим AB●AD=AC². Аналогично из равенства cos.(ÐB)== получим равенство AB●BD=BC². Складывая полученные равенства почленно и замечая, что AB+BD=AB, получим равенство AC²+BC²=AB●AD+AB●BD=AB(AD+BD)=AB².

Теорема доказана.

9

Заключение.

При выполнении работы было найдено 10 способов доказательства теоремы Пифагора. На мой взгляд, наиболее лёгким является доказательство, основанное на теории подобия треугольников.

10

Список литературы:

1. Г.И. Глейзер «История математики в школе»   Москва «Просвещение» 1964год

2. Л.С.Атанасян «Геометрия 7-9»

3. А.В.Погорелов «Геометрия 7-11»

4. А.Н. Шыныбеков «Геометрия 8»

5. А.Н. Шыныбеков «Алгебра 8»

11

Содержание

1.     Абстракт………………………………………………….1

2.     Этапы исследования……………………………………..1

3.     Аннотация………………………………………………..2

4.     Из истории……………………………………………….3

5.     Теорема Пифагора………………………………………5

6.     Заключение …………………………………………….10

7.     Список литературы…………………………………….11