Программа элективного курса по математике «Случайная закономерность или закономерная случайность?» (7 класс)
Элективный курс
«Случайная закономерность или закономерная случайность?»
для учащихся 8 класса
Автор: учитель МАОУ СОШ№21
г. Кунгур, Пермский край,
Питиримова М. С.
2017
Программа элективного курса «Случайная закономерность или закономерная случайность?»
Пояснительная записка
До настоящего времени в школьном курсе математики и других естественных наук господствовала только одна идея – о существовании однозначных связей между явлениями и событиями. Эти связи представлены в форме законов физики, химии, математики. Но окружающий нас мир полон случайностей. Это землетрясения, ураганы, подъемы и спады экономического развития, войны, болезни, случайные встречи. Возникает необходимость формирования у школьников вероятностного мышления.
Без знания понятий и методов теории вероятностей и статистики невозможна организация эффективного конкурентоспособного производства, внедрения новых лекарств и методов лечения в медицине, обеспечение страховой защиты граждан от непредвиденных обстоятельств.
Предлагаемый курс «Случайная закономерность или закономерная случайность?» дает возможность учащимся получить представления о статистических закономерностях в реальном мире и о различных способах их изучения.
Познавательный материал курса будет способствовать формированию функциональной грамотности – умению воспринимать и анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, производить простейшие вероятностные расчеты.
Значительное место в курсе уделено практической направленности материала, его приложений, мотивации процесса познания.
Курс рассчитан на 13 учебных часов. Итогом курса является выполнение учениками проектных работ и их защита.
Цель курса:
- формирование математического вероятностного стиля мышления у учащихся девятого класса.
Задачи:
- развивать у учащихся представления о вероятностно-статистических закономерностях в окружающем мире;
- развивать логическое мышление;
- учить вычислять вероятность случайного события;
- совершенствовать интеллектуальные умения учащихся.
Основные требования к уровню подготовки учащихся:
В результате изучения курса учащиеся должны:
- понимать вероятностный характер процессов окружающего мира;
- уметь предугадывать возможные исходы события;
- уметь вычислять вероятность случайного события, пользуясь различными способами;
- анализировать реальные числовые данные.
Критерии оценки: оценивание учащихся осуществляется по пятибалльной шкале.
Почасовое тематическое планирование
|
Номер темы |
Содержание материала |
Кол-во часов |
|
1 |
Описательная статистика |
2 |
|
2 |
Комбинаторика |
1 |
|
3 |
Математическое описание случайных событий |
4 |
|
4 |
Случайные величины |
2 |
|
5 |
Разработка проектов |
3 |
|
6 |
Защита проектов |
1 |
Содержание программы
Тема 1. Описательная статистика (2 ч)
Среднее арифметическое, медиана, мода, размах числового ряда.
Результаты обучения:
- знать характеристики числового ряда;
- уметь вычислять моду, медиану, среднее арифметическое, размах числового ряда;
- уметь использовать характеристики для описания числовых рядов.
Тема 2. Комбинаторика (1 ч)
Перестановки, сочетания, размещения.
Результаты обучения:
- знать формулы комбинаторики;
- уметь использовать формулы комбинаторики для решения задач.
Тема 3. Математическое описание случайных событий (5 ч)
Случайные опыты. Элементарные события. Статистическая вероятность. Классическое определение вероятности. Благоприятствующие события. Вероятности событий. Противоположные события. Объединение, пересечение событий. Несовместные события. Правило сложения вероятностей. Независимые повторные испытания. Формула Бернулли.
Результаты обучения:
- иметь представление об элементарном событии, равновозможных, благоприятствующих, противоположных и несовместных событиях;
- уметь вычислять вероятность элементарного события в опыте с равновозможными событиями;
- знать классическое, статистическое определения вероятности;
- уметь использовать правила сложения вероятностей;
- знать формулу Бернулли, уметь применять ее при решении задач.
Тема 4. Случайные величины (2 ч)
Примеры случайной величины, распределение вероятностей случайной величины. Математическое ожидание, дисперсия. Закон больших чисел.
Результаты обучения:
- уметь приводить примеры случайных величин;
- понимать, что такое распределение случайной величины;
- уметь составлять таблицы распределения случайных величин;
- знать определение математического ожидания конечной случайной величины;
- уметь вычислять математическое ожидание случайной величины;
- знать свойства математического ожидания;
- уметь использовать свойства математического ожидания при решении простых задач;
- знать, что важным свойством распределения случайной величины является рассеивание случайной величины;
- уметь вычислять дисперсию и стандартное отклонение случайной величины;
- знать, что такое закон больших чисел
- уметь применять закон больших чисел, при решении задач.
Тема 5. Разработка проектов (3 ч)
Самостоятельная работа учащихся и консультация учителя.
Результаты обучения:
- уметь исследовать, проектировать ситуацию;
- уметь добывать нужную информацию самостоятельно;
- уметь анализировать полученную информацию.
Тема 6. Защита проектов (1ч)
Результаты обучения:
- уметь представлять результаты своего труда.
Литература
1. Лютикас, В. С. Факультативный курс по математике. Теория вероятностей.
2. Макарычев, Ю. К, Миндюк, Н. Г. Алгебра: элементы статистики и теории вероятностей: учебное пособие для 7 – 9 классов общеобразовательных учреждений / под ред. С. А. Теляковского.
3. Математика. 10-11 классы: элективный курс «В мире закономерных случайностей»/ авт.-сост. В.Н. Студенецкая, Л.Г. Козлова и другие
4. Мордкович, А. Г., Семенов, П. В. События. Вероятности. Статистическая обработка данных. Дополнительные параграфы к курсу алгебры 7–9 классов общеобразовательных учреждений.
Тема: Описательная статистика
Средние величины.
Цель: повторение, изучение и обобщение материала по теме «Описательная статистика»
Задачи: - научить учащихся вычислять моду, медиану, среднее арифметическое, размах числового ряда;
- сформировать умение использовать характеристики для описания числовых рядов;
- развивать логическое мышление, кругозор, математическую речь, интерес к математике.
Ход занятия
1. Средние величины
Средней величиной называют показатель, который характеризует обобщенное значение признака или группы признаков в исследовании.
Средние величины используются на этапе обработки и обобщения полученных первичных статистических данных. Потребность определения средних величин связана с тем, что у различных единиц исследуемых совокупностей индивидуальные значения одного и того же признака, как правило, неодинаковы.
Рассмотрим средние величины: среднее арифметическое, моду, медиану.
Средним арифметическим нескольких чисел называется число, равное отношению суммы этих чисел к их количеству.
![]()
В статистике эту величину называют еще средним значением или выборочным средним. В большинстве реальных исследований именно среднее арифметическое несет наиболее важную информацию об изучаемом явлении. Достаточно вспомнить выражения: «средний балл», «средняя зарплата», «средний доход», хорошо знакомые и понятные большинству людей.
Рассмотрим пример: Пусть ученик получил в течение первой учебной четверти следующие отметки по алгебре: 5, 3, 4, 4, 5, 5 , 4, 5, 4, 5.
Найдем его средний балл, то есть среднее
арифметическое всех членов ряда: ![]()
Модой числового ряда называют число, которое встречается в этом ряду наиболее часто.
Найдем моду для нашего примера. Она равна ![]() .
.
Именно эта величина, скорее всего, будет главным ориентиром для учителя при выставлении итоговой оценки.
В отличие от среднего арифметического, которое можно вычислить для любого числового ряда, моды у ряда может вообще не быть. Например, тот же ученик получил по русскому языку следующие отметки: 3, 4, 2, 5. Каждая отметка встречается в этом ряду только один раз, и среди них нет числа, встречающегося чаще других. Значит, у него нет моды.
Ряд, имеющий единственную моду, называют унимодальным, а ряд, у которого нет моды (или мод несколько) – полимодальным.
Еще одной важной средней характеристикой числового ряда является его медиана – число ряда, которое делит его ровно пополам.
Медианой числового ряда называют число этого ряда (или полусумму двух его чисел), слева и справа от которого на числовой прямой лежит одинаковое количество членов ряда.
Чтобы найти медиану числового ряда, нужно его сначала упорядочить – составить ранжированный ряд. В нашем примере с оценками он выглядит так: 3, 4, 4, 4, 4, 5, 5, 5, 5, 5.
Если ряд содержит нечетное число членов, то
нужно взять число, которое находится посредине, если ряд содержит четное число
членов, то нужно взять два средних числа и найти его полусумму, например, ![]()
Особенности средних величин
Далеко не всегда имеет смысл вычислять все три характеристики, так как во многих ситуациях какая-то характеристика может не иметь никакого содержательного смысла.
Задача
Гвозди в магазине продают на вес. Чтобы оценить, сколько гвоздей содержится в 1 килограмме, Вася решил найти массу одного гвоздя. Для повышения точности он взвесил на лабораторных весах несколько разных гвоздей и получил следующий ряд чисел (масса гвоздей в граммах): 4,47; 4,44; 4,64; 4,32; 4,45; 4,32; 4,54; 4,58.
Какую из характеристик ему следует взять в качестве оценки веса одного гвоздя? Найдем все три характеристики.
![]() ,
,
4,32; 4,32; 4,44; 4,45; 4,47; 4,54; 4,58; 4,64
Мо=4,32, ![]() .
.
Самой подходящей по смыслу характеристикой является среднее арифметическое. Несильно отличается от него и медиана, которая тоже пригодна для оценки средней массы. А мода здесь не подойдет, поскольку все значения полученного ряда разные, и совпадение двух чисел 4,32 вряд ли отображает какую-то закономерность в изготовлении гвоздей.
Таким образом, при формальном существовании всех трех характеристик разумно использовать только одну них.
Приведем пример, когда мода содержит больше полезной информации.
Пример. Перед нами ранжированный ряд, представляющий данные о времени дорожно-транспортных происшествий на улицах города в течение одних суток (в виде ч: мин):
0:15, 0:55, 1:20, 3:20, 4:10, 6:30, 7:15, 7:45, 8:40, 9:05, 9:20, 9:40, 10:15, 11:30, 12:10, 12:15, 13:10, 13:50, 14:10, 14:20, 14:25, 15:20, 15:45, 16:20, 16:25, 17:05, 17:30, 17:45, 17:55, 18:05, 18:15, 18:45, 18:50, 19:45, 19:55, 20:30, 20:40, 21:30, 21:45, 22:10, 22:35.
Как и для любого ряда, в данном случае мы можем найти среднее арифметическое – оно равно 13:33. Однако, вряд ли имеет какой-то смысл утверждение типа «аварии на улицах города происходят в среднем в 13 часов 33 минуты». В то же время, если сгруппировать данные этого ряда в интервалы, можно найти такой временной интервал, когда происходит наибольшее количество ДТП (такую характеристику называют интервальной модой). Получив такую характеристику, соответствующие службы должны серьезно проанализировать, почему именно в этот временной интервал происходит наибольшее количество происшествий, и попытаться устранить их причины.
И, наконец, пример, где удобнее пользоваться медианой.
На школьной спартакиаде проводится несколько квалификационных забегов на 100 метров, по результатам которых в финал выходит ровно половина от числа всех участников. Перед вами результаты всех спортсменов. Какой результат позволяет пройти в финал?
15,5; 16,8; 21,8; 18,4; 16,2; 32,3; 19,9; 15,5; 14,7; 19,8; 20,5; 15,4.
Проранжируем ряд, то есть расставим числа в порядке возрастания:
14,7; 15,4; 15,5; 15,5; 16,2; 16,8; 18,4; 19,8; 19,9; 20,5; 21,8; 32,3.
Здесь для ответа на вопрос нужно вычислить медиану: ![]() . Спортсменов, которые имеют
результат выше найденного, будет как раз половина от числа всех участников. А
вот результат выше среднего арифметического, которое равно:
. Спортсменов, которые имеют
результат выше найденного, будет как раз половина от числа всех участников. А
вот результат выше среднего арифметического, которое равно:
![]() , еще не позволяет
рассчитывать на выход в финал: в списке есть спортсмен с результатом 18,4,
который не попадает в финал. Мода этого ряда равна Мо=15,5 и дает
слишком завышенную оценку для «среднего результата».
, еще не позволяет
рассчитывать на выход в финал: в списке есть спортсмен с результатом 18,4,
который не попадает в финал. Мода этого ряда равна Мо=15,5 и дает
слишком завышенную оценку для «среднего результата».
Занятие 2
Размах числового ряда
Цель: повторение, изучение и обобщение материала по теме «Описательная статистика»
Задачи: - научить учащихся вычислять размах числового ряда;
- закрепить умение решать задачи на нахождение описательных характеристик числового ряда.
Ход занятия
1. Размах числового ряда
Числовые характеристики, позволяющие оценить поведение числового ряда «в среднем», далеко не всегда дают полное представление о поведении изучаемой величины. Например, на планете Меркурий средняя температура +150 . исходя из этого статистического показателя, можно подумать, что на Меркурии умеренный климат, удобный для жизни людей. Однако на самом деле это не так. Температура на Меркурии колеблется от -1500 до +3500.
Значит, чтобы получить представление о поведении числового ряда, помимо средних характеристик надо знать характеристики разброса, или рассеяния, показывающие, насколько значения ряда различаются между собой, как сильно они разбросаны, рассеяны вокруг средних. Простейшей такой характеристикой является размах.
Размах – это разность наибольшего и наименьшего значений ряда данных.
Пример 1. Для температуры на Меркурии, например, размах равен
3500-(-1500)=5000. Конечно, такого перепада температур человек выдержать не может.
Пример 2. В течение суток отмечали каждые два часа температуру воздуха в городе:
|
Время, час |
0 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
22 |
|
Температура, оС |
3 |
4 |
4 |
6 |
9 |
11 |
11 |
11 |
9 |
6 |
4 |
3 |
Размах данного ряда, равный 11-3=8, характеризует колебание температуры воздуха в течение этих суток.
Решение задач
Задача 1
На стадионе «Локомотив» была зафиксирована следующая посещаемость первых четырех футбольных матчей: 24000, 18000, 22000, 24000. Какова средняя посещаемость этих матчей? Сколько зрителей должно посетить следующий матч, чтобы посещаемость выросла?
![]() .
.
Средняя посещаемость вырастет, если на следующий матч придет больше 22000 зрителей.
Задача 2
Каждое число исходного числового ряда увеличили на 10. Что произойдет с его средним арифметическим, модой и медианой?
(они увеличатся на 10)
Задача 3. Найдите для числового ряда 1, 2, 3, 4, х все возможные значения х, при которых:
а) среднее арифметическое ряда равно 3;
б) мода равна 3;
в) медиана равна 3.
Решение.
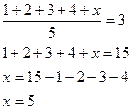 а)
а)
б) Мо=3 =>х=3
в) Ме=3 => х – любое число, больше 3.
Задача 4
Числовой ряд содержит 10 единиц и некоторое число х:
1, 1, 1, 1, 1, 1, 1, 1, 1, 1, х.
Найдите для этого ряда все числовые характеристики: среднее арифметическое, моду, медиану, размах. Какие их них зависят от х?
Решение.
1. ![]() ;
;
2. Мо=1;
3. Ме=1;
4. если х<0, то размах =1-х;
если x=0, то размах =1-0=1;
если x>0, то размах =х-1.
От значения х зависят среднее арифметическое и размах.
Задача 5
Известно, что ряд данных состоит из натуральных чисел. Может ли для этого ряда быть дробным числом:
а) среднее арифметическое;
б) размах;
в) мода;
г) медиана.
(да)
(нет)
(нет)
(да)
Задача 6
Напишите эссе на тему «Роль средних характеристик как источников информации».
Тема: Комбинаторика.
Перестановки. Размещения. Сочетания.
Цель: изучение элементов комбинаторики
Задачи: - познакомить учащихся с элементами комбинаторики;
- учить решать задачи с помощью элементов комбинаторики;
- развивать логическое мышление, кругозор, математическую речь, интерес к математике.
Ход занятия
1. Сообщение темы и цели занятия
В науке и практике часто встречаются задачи, решая которые, приходится составлять различные комбинации из конечного числа элементов и подсчитывать число комбинаций. Решать такие задачи помогает комбинаторика – раздел математики, в котором исследуются и решаются задачи выбора элементов из исходного множества и расположения их в некоторой комбинации, составленной по заданным правилам.
Перестановка
Простейшими комбинациями, которые можно составить из элементов конечного множества, являются перестановки.
Пример. Сколькими способами можно построить трех человек в шеренгу?
Решение: а в с, а с в, в а с, в с а, с а в, с в а.
Pn –
число перестановок. ![]()
Перестановкой из n элементов называется каждое расположение этих элементов в определенном порядке.
![]()
где n! называется факториалом числа n. Это произведение первых натуральных n чисел от 1 до n.
Задача 1. В автосервис приехали 5 машин для ремонта. Сколько существует способов выстроить их в очередь на обслуживание?
Решение: ![]()
Задача 2. Сколько различных последовательностей можно составить из букв слова (необязательно осмысленных)?
а) учебник;
б) автор;
в) фонарь.
Решение: ![]() .
.
![]() .
.
![]() .
.
Размещение
Размещением из n элементов по k ![]() называется
любое множество, состоящее из любых k элементов, взятых в определенном порядке из n элементов.
называется
любое множество, состоящее из любых k элементов, взятых в определенном порядке из n элементов.
![]() .
.
Задача 1. Учащиеся 2 класса изучают 8 предметов. Сколькими способами можно составить расписание на 1 день, чтобы в нем было 4 различных предмета?
Решение: ![]() .
.
Задача 2. Сколькими способами 6 студентов, сдающих экзамен, могут занять место в аудитории, в которой стоит 20 одноместных столов?
Решение: ![]()
Сочетание
Сочетанием из n элементов по k называется любое множество, составленное из k элементов, выбранных из данныхn элементов.
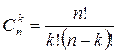
Задача 1. Сколькими способами можно распределить между шестью различными лицами две одинаковые путевки?
Решение: ![]()
Задача 2. В классе 25 учеников. Сколькими способами учитель может выбрать в этом классе для опроса:
а) 5 различных учеников;
б) 6 различных учеников;
в) 20 различных учеников.
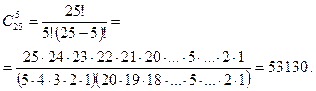 Решение:
Решение:
а)
б) ![]()
в) ![]()
2. Самостоятельная работа
Задача 1
На дверях четырех одинаковых кабинетов надо повесить таблички с фамилиями четырех заместителей директора. Сколькими способами это можно сделать?
Решение: ![]() .
.
Задача 2
Сколькими способами могут быть разделены первая, вторая и третья премии между 15 участниками конкурса?
Решение: ![]() .
.
Задача 3
Иван Николаевич купил билет лото «6 из 49». Он должен зачеркнуть 6 номеров из 49. сколько существует способов это сделать?
Решение: ![]()
Тема: Математическое описание случайных событий
Занятие 1
Случайные опыты. Элементарные события.
Статистическая вероятность
Цель: изучение математического описания случайных событий
Задачи: - ввести понятия: случайный опыт, элементарные события, статистическая вероятность;
- учить решать задачи на выявление случайных, элементарных событий;
- развивать логическое мышление, кругозор, математическую речь, интерес к математике.
Ход занятия
1. Случайные опыты. Элементарные события
Как известно, в повседневной жизни, в практичной и научной деятельности мы наблюдаем различные явления, которые называем событиями.
Событие, которое может произойти, а может и не произойти, называют случайным событием.
Случайное событие является следствием очень многих обстоятельств, точно учесть которые невозможно. Например, если один раз бросить монету, то нельзя сказать, что упадет она «орлом» кверху или нет. Если же бросить монету 1000 раз, то примерно 500 раз появится «орел». Такие опыты проводились много раз. В таблице приведены результаты некоторых из них.
|
|
Число бросаний |
Число появлений «орла» |
|
Ж. Бюффон |
4040 |
2048 |
|
К. Пирсон |
12000 |
6019 |
|
К. Пирсон |
24000 |
12012 |
Бюффон Жорж Луи Леклерк (1707-1788) – французский естествоиспытатель, первым стал заниматься задачами на геометрические вероятности.
Пирсон Карл (Чарльз) (1857-1936) – английский математик, философ. Основные его труды относятся к математической статистике.
Случайное событие может осуществиться только при определенных условиях. Если нет таких условий, то нет и события. Например, «орел» появляется только при бросании монеты.
Те условия и действия, при которых может осуществиться случайное событие, принято называть случайным опытом, или экспериментом. В теории вероятностей принято считать случайными все события, связанные со случайным экспериментом, в том числе: невозможные, которые никогда не могут произойти; достоверные, которые происходят при каждом эксперименте.
Каждый эксперимент имеет свой исход, то есть значение наблюдаемого признака, непосредственное получение по окончании эксперимента. Каждый эксперимент заканчивается одним и только одним исходом.
Необходимо четко различать понятия исход эксперимента и событие.
Пример 1. Бросание игральной кости. Исход эксперимента: номер верхней грани кубика; возможно 6 разных исходов.
События:
А – выпало четное число очков (исходы 2, 4, 6);
В – выпало число очков, кратное 3 (исходы 3, 6);
С – выпало более 4 очков (исходы 5, 6).
Если бросили кубик, и выпало 1, то не наступило ни одно из указанных событий; если выпало 6, то наступили все три события одновременно.
Таким образом, в результате опыта могут произойти различные случайные события. Событие А состоит из трех более простых событий, события В и С – из двух.
События, которые нельзя разделить на более простые, называют элементарными событиями.
В каждом опыте можно выделить такие элементарные события, из которых состоят все остальные события. В результате опыта наступает только одно элементарное событие (исход).
Пример 2. 1) Бросание одной игральной кости – 6 элементарных событий.
2) Бросание двух игральных кубиков.
Элементарным событием в данном случае является
пара чисел. Количество элементарных событий: ![]() .
.
Устное упражнение.
Определить вид события (невозможное, достоверное, случайное) в данном эксперименте: из списка журнала 9 класса выдран один ученик:
1) это мальчик;
2) выбранному ученику 15 лет;
3) выбранному ученику 15 месяцев;
4) этому ученику больше двух лет.
Решение задач
1. Сколько элементарных событий при четырех бросаниях монеты?
Решение: одно бросание сопровождается двумя
исходами, значит, при четырех бросаниях количество исходов ![]() .
.
Ответ: 16.
2. Игральную кость бросают трижды. Найти число элементарных событий, при которых в сумме выпало:
а) 2 очка;
б) 3 очка;
в) 4 очка;
г) 18 очков.
Решение:
а) событие невозможное;
б) необходимый исход: 1 1 1 – возможен только один;
в) необходимые для условия задачи исходы: 1 1 2; 121; 211;
г) возможен только один исход: 6 6 6.
3. Охарактеризуйте событие, о котором идет речь, как достоверное, невозможное или случайное.
а) день рождения моего друга – число меньшее, чем 32; (д)
б) на уроках физкультуры ученики решали математические задачи; (н)
в) на уроках математики ученики решали примеры; (д)
г) из отрезка [1, 2] наугад взяли 1 число, оно оказалось смешанным; (с)
д) вверх подкинули монету, и она упала на землю «орлом». (с)
2. Статистическая вероятность
Событие называется случайным, если при некотором комплексе условий оно может либо произойти, либо не произойти.
Вероятность случайного события – это числовая мера его правдоподобности. Отношение числа тех опытов, в которых событие С произошло, к общему числу проведенных опытов называется частотой случайного события С в этой серии экспериментов.
Пусть проведена серия из n испытаний и подсчитано число случаев, в которых событие А произошло.
Относительной частотой случайного события называется отношение числа случаев появления этого события к общему числу испытаний.
То есть, относительная частота события – это дробь ![]() , в которой m – число тех испытаний, в которых событии произошло, n – общее число испытаний. Так как m и n –
неотрицательные числа и
, в которой m – число тех испытаний, в которых событии произошло, n – общее число испытаний. Так как m и n –
неотрицательные числа и ![]() , то
относительная частота удовлетворяет неравенствам
, то
относительная частота удовлетворяет неравенствам ![]() .
.
Событие называется достоверным, если в рассматриваемом испытании оно обязательно произойдет. Событие называется невозможным, если в рассматриваемом испытании оно произойти не может.
Очевидно, что относительная частота достоверного события равна единице, а относительная частота невозможного события равна нулю.
Таким образом, вероятность – это предельное значение частоты в бесконечной серии экспериментов.
Занятие 2
Классическое определение вероятности. Благоприятствующие события. Вероятности событий. Противоположные события
Цель: изучение математического описания случайных событий
Задачи: - дать понятия: классическое определение вероятности, благоприятствующие события, вероятности событий, противоположные события;
- учить решать задачи на классическое определение вероятности;
- учить находить и различать благоприятствующие события, вероятности событий, противоположные события;
- развивать логическое мышление, кругозор, математическую речь, интерес к математике.
Ход занятия
1. Классическое определение вероятности
Очень часто в рассматриваемых явлениях действительности имеется некоторая симметрия, позволяющая говорить о равновозможности событий. Равновозможными называются элементарные события, шансы которых одинаковы. Так, при бросании игральной кости, на верхней грани может появиться любая цифра: 1, 2, 3, 4, 5 или 6. Ни одна из них не имеет преимуществ перед другой.
Говорят, что существует 6 равновозможных исходов этого испытания: выпадение очков 1, 2, 3, 4, 5 и 6.
Рассмотрим событие В, которое означает
выпадение числа очков, кратного 3. это событие происходит лишь при двух
исходах: когда выпало 3 очка и когда выпало 6. эти исходы называют
благоприятными исходами события В. Отношение числа благоприятных исходов к
числу всех равновозможных исходов равно ![]() .
Это отношение называют вероятностью события В и пишут:
.
Это отношение называют вероятностью события В и пишут: ![]() .
.
Классическим определением вероятности: Вероятностью события называется отношение числа благоприятных для него исходов к числу всех равновозможных исходов.
![]() - формула
Лапласа (формула классической вероятности),
- формула
Лапласа (формула классической вероятности),
где mA – благоприятные исходы события А, n – равновозможные исходы.
С помощью формулы Лапласа можно решать задачи на нахождение вероятности события.
Задача
В классе 32 ученика. Двое из них выбраны совсем случайно и посажены за первую парту. Какова вероятность того, что оба они в списке значатся среди первых десяти учеников?
Решение. ![]()
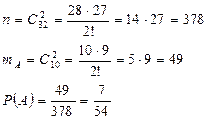
2. Благоприятствующие события. Вероятности событий
В ходе опыта могут возникать более сложные случайные события: например, «выпало четное число очков» при бросании игральной кости. У таких событий тоже есть вероятности.
Обозначим события А, В, С, …
Элементарные события, при которых наступает событие А, называют благоприятствующими событию А.
Пример. Андрей, Борис и Владимир встают в очередь. Всего возможных событий 6: АБВ, АВБ, БАВ, БВА, ВАБ, ВБА. Рассмотрим событие «В стоит первым». Это события ВАБ, ВБА. Значит, данному событию благоприятствуют 2 элементарных события.
Вероятность события равна сумме вероятностей элементарных событий, благоприятствующих этому событию. P(A)=P(a)+P(b)+P(c)+P(d).
Число элементарных событий может быть различным. Вероятности всех элементарных событий неотрицательны и в сумме дают 1. Значит, вероятность любого события А также неотрицательна и в сумме не превосходит 1:
Если Р(А)=0, то событие называется невозможным.
Если Р(А)=1, то событие называется достоверным (ему благоприятствуют все элементарные события).
События, которые имеют одинаковые вероятности, – равновероятные.
Задача
Витя забыл две последние цифры номера телефона приятеля и набрал их наугад. С какой вероятностью этот звонов попадет к приятелю?
Решение.
Всего возможно 100 исходов (102), но благоприятный исход
только 1. Отсюда, ![]()
3. Противоположные события. Рассмотрим какое-либо событие А. Ему благоприятствуют некоторые элементарные события. Рассмотрим теперь все прочие элементарные события этого опыта, то есть те, которые не благоприятствуют событию А. Соберем все эти элементарные события вместе. Так мы получим новое событие. Это событие событием, противоположным событию А.
Событием, противоположным событию А, называется событие, которому благоприятствуют все элементарные события, не благоприятствующие событию А.
Событие, противоположное событию А, обозначается ![]() . Если событие В противоположно
событию А, то есть
. Если событие В противоположно
событию А, то есть ![]() , то
, то ![]() . Поэтому события А и
. Поэтому события А и ![]() называются взаимно
противоположными или дополнением друг друга.
называются взаимно
противоположными или дополнением друг друга.
Пример. Событие А: «при бросании игральной кости выпало 5 или 6 очков».
Событие ![]() : «при бросании игральной
кости выпало 1, 2, 3, 4 очка».
: «при бросании игральной
кости выпало 1, 2, 3, 4 очка».
Взаимно противоположные события одновременно произойти не могут, но
какое-либо из них происходит обязательно. Поэтому ![]() .
.
Сумма вероятностей взаимно противоположных событий равна 1.
Следовательно, ![]() и
и ![]() .
.
Пример. Какова вероятность того, что при бросании двух игральных костей на них выпадет неодинаковое число очков?
Решение: обозначим описанное событие А. Тогда ![]() :
«на обеих костях выпало одинаковое число очков».
:
«на обеих костях выпало одинаковое число очков».
Событию ![]() благоприятствуют 6
элементарных событий:
благоприятствуют 6
элементарных событий:
(1,1), (2,2), (3,3), (4,4), (5,5), (6,6).
Вероятность каждого из них равна 1/36, следовательно,
![]() .
.
Значит, ![]() .
.
Решение задач
Докажите, что события А и В не могут быть взаимно противоположными, если:
а) Р(А)=0,7; Р(В)=0,45;
б) Р(А)=0,3; Р(В)=0,7.
![]()
Решение. а) 0,7+0,45=1,15=> события А и В не могут быть взаимно противоположными;
б) 0,3+0,7=1 => события А и В могут быть взаимно противоположными.
Занятие 3
Объединение и пересечение событий. Несовместные события. Правило сложения вероятностей
Цель: изучение математического описания случайных событий
Задачи:- дать понятия: объединение и пересечение событий, несовместные события;
- учить решать задачи на объединение и пересечение событий;
- учить решать задачи на правило сложения вероятностей;
- развивать логическое мышление, кругозор, математическую речь, интерес к математике.
Ход занятия
1. Объединение и пересечение событий
Объединение событий
Пусть А и В – два события, относящиеся к одному
случайному опыту. Рассмотрим те элементарные события, которые благоприятствуют
событию А, и те, которые благоприятствуют событию В. Все вместе эти
элементарные события благоприятствуют новому событию – объединению событий А и
В, которое обозначается ![]() .
.
Событие ![]() наступает,
если наступает хотя бы одно из событий А или В, то есть это означает, что
наступает либо А, либо В, либо А и В вместе.
наступает,
если наступает хотя бы одно из событий А или В, то есть это означает, что
наступает либо А, либо В, либо А и В вместе.
Пример. Продавщица выбирает два костюма для того, чтобы поместить их в витрине магазина. В ассортименте есть черные (Ч) и синие (С) костюмы. Элементарные события этого случайного опыта представляют собой пары костюмов, которые мы можем условно обозначить парами букв, указывающих цвета выбранных костюмов: ЧС, ЧЧ, СС, СЧ.
Событие А состоит в том, что первый костюм черного цвета. Этому событию благоприятствуют элементарные события ЧС и ЧЧ.
Событие В состоит в том, что второй костюм черного цвета. Этому событию благоприятствуют элементарные события СЧ и ЧЧ.
Объединению событий ![]() в
этом случае благоприятствуют элементарные события, благоприятствующие хотя бы
одному из двух событий А и В, то есть элементарные события ЧС, ЧЧ и СЧ (т. е.
хотя бы один костюм черного цвета).
в
этом случае благоприятствуют элементарные события, благоприятствующие хотя бы
одному из двух событий А и В, то есть элементарные события ЧС, ЧЧ и СЧ (т. е.
хотя бы один костюм черного цвета).
Задача
Событию А благоприятствуют 17 элементарных событий, событию В – 32 элементарных события. Причем, эти события не имеют общих элементарных событий . Всего в опыте 60 различных элементарных событий.
а) Сколько элементарных событий
благоприятствуют событию ![]() ?
?
б) Сколько элементарных событий
благоприятствуют событию ![]() ?
?
в) Сколько элементарных событий
благоприятствуют событию ![]() ?
?
г) Сколько элементарных событий
благоприятствуют событию ![]() ?
?
Решение.
а) 60-32=28;
б) 60-17=43;
в) 60-(17+32)=11;
г) (28+43)-11=60.
Пересечение событий
Возьмем два события – А и В. Предположим, что
есть элементарные события, благоприятствующие и А, и В. Взяв все эти
элементарные события, мы получим новое событие – пересечение событий А и В,
которое обозначается ![]() . Событие наступает, если
наступают оба события – А и В.
. Событие наступает, если
наступают оба события – А и В.
Если события А и В не имеют общих
благоприятствующих элементарных событий, то они не могут наступить одновременно
в ходе одного и того же опыта. Такие события называют несовместными, а их
пересечение – пустым множеством. Оно обозначается символом Æ. То есть ![]() =Æ.
=Æ.
Вероятность пересечения несовместных событий равна 0.
Пример. События «8 Марта приходится на пятницу» и «8 Марта приходится на субботу» являются несовместными в одном и том же году.
Задача
В ходе некоторого опыта событию А
благоприятствуют 6 элементарных событий, событию В – 8 элементарных событий.
При этом два элементарных события благоприятствуют событию ![]() . Сколько элементарных событий
благоприятствует событию:
. Сколько элементарных событий
благоприятствует событию:
а) «событие А наступает, а В – нет»;
б) «событие В наступает, а А – нет».
Решение.
а) 6-2=4;
б) 8-2=6.
2. Несовместные события. Правило сложения вероятностей
Несовместные события – это события, которые не имеют общих благоприятных элементарных событий.
Вероятность одновременного их наступления равна
0, то есть ![]() .
.
Вероятность объединения несовместных событий
равна сумме их вероятностей:![]() .
.
Пример. Игральную кость бросают дважды. Событие А состоит в том, что в первый раз выпало больше очков, чем во второй. Событие В состоит в том, что во второй раз выпало больше очков, чем в первый.
Решение:
Составим таблицу элементарных событий, благоприятствующих каждому их этих событий.
|
1; 1 |
1; 2 |
1; 3 |
1; 4 |
1; 5 |
1; 6 |
|
2; 1 |
2; 2 |
2; 3 |
2; 4 |
2; 5 |
2; 6 |
|
3; 1 |
3; 2 |
3; 3 |
3; 4 |
3; 5 |
3; 6 |
|
4; 1 |
4; 2 |
4; 3 |
4; 4 |
4; 5 |
4; 6 |
|
5; 1 |
5; 2 |
5; 3 |
5; 4 |
5; 5 |
5; 6 |
|
6; 1 |
6; 2 |
6; 3 |
6; 4 |
6; 5 |
6; 6 |
События А и В несовместны.
![]() .
.
Тогда вероятность события ![]() равна
равна ![]() .
.
Задача
События А и В несовместны. Найдите вероятность их объединения, если:
а) Р(А)=0,2; Р(В)=0,4;
б) Р(А)=0,5; Р(В)=0,2;
в)
Р(А)=1-a; Р(В)=1-b, где ![]() ,
, ![]() ;
;
г)
Р(А)=![]() ; Р(В)=ab, где
; Р(В)=ab, где ![]() .
.
Решение.
а) ![]()
б) ![]()
в) ![]()
г) ![]()
Домашнее задание.
Составить 5 различных задач на отыскание вероятности событий.
Занятие 4
Формула сложения вероятностей. Независимые повторные испытания. Формула Я. Бернулли
Цель: изучение математического описания случайных событий
Задачи:- объяснить формулу сложения вероятностей для любых событий;
- учить решать задачи, используя формулу сложения вероятностей;
- познакомить учащихся со схемой Бернулли;
- сформировать умения применять схему при решении задач;
- развивать логическое мышление, кругозор, математическую речь, интерес к математике.
Ход занятия
1. Формула сложения вероятностей
Если события А и В не являются несовместными, то есть могут оба
наступить в результате опыта, то к ним нельзя применить формулу ![]() .
.
Пример. Бросают две игральные кости. Событие А – «на первой кости выпало меньше 3 очков». Событие В – «на второй кости – меньше 3 очков».
Событию А благоприятствуют 12 элементарных событий. Событию В тоже
благоприятствуют 12 элементарных событий. Событию ![]() благоприятствуют
20 элементарных событий. Поэтому
благоприятствуют
20 элементарных событий. Поэтому ![]() ,
, ![]() ,
, ![]() ,
то есть
,
то есть ![]() .
.
Получается, что формула ![]() для этих
событий применять нельзя. Как быть?
для этих
событий применять нельзя. Как быть?
Рассмотрим такие события: событие С – «наступило А, но не наступило В»
и событие Д – «наступило В, но не наступило А». на диаграмме видно, что события
С и ![]() несовместны, так как соответствующие
фигуры не имеют общих точек. Вместе эти события образуют событие А. Поэтому по
правилу сложения вероятностей для несовместных событий находим:
несовместны, так как соответствующие
фигуры не имеют общих точек. Вместе эти события образуют событие А. Поэтому по
правилу сложения вероятностей для несовместных событий находим: ![]() . Точно так же получаем
. Точно так же получаем ![]() .
.
Сложив эти равенства почленно, получим:
![]()
События С, Д и ![]() несовместны и образуют
событие
несовместны и образуют
событие ![]() .
.
Получаем формулу:
![]() , откуда
, откуда ![]() .
.
Эта формула справедлива для любых событий.
Вероятность объединения двух событий равна сумме их вероятностей минус вероятность пересечения.
Задача
Вероятность того, что по дороге из школы домой вы встретите черную кошку, равна 0,1. Вероятность того, что по дороге из школы домой вы встретите злую собаку, равна 0,4. Вероятность того, что вам встретятся и черная кошка и злая собака, равна 0,04.
а) Найдите вероятность, что вам встретится хотя бы одно из этих животных.
б) Найдите вероятность, что вы не встретите ни черную кошку, ни злую собаку.
Решение.
а) ![]() ;
;
б) 1-0,46=0,54.
2. Независимые повторные испытания. Формула Я. Бернулли
Многие задачи в теории вероятностей сводятся к следующей схеме, которая называется схемой Я. Бернулли по имени математика, который первым ее рассмотрел.
Пусть производится п испытаний, причем вероятность появления
события А в каждом испытании равна р, тогда вероятность непоявления
события – q=1-p. Вычислим вероятность того, что при п испытаниях
событие А произойдет m раз, ![]() . Эта вероятность обозначается
. Эта вероятность обозначается ![]() и находится по формуле
и находится по формуле ![]() .
.
Пример. Какова вероятность того, что при 10 бросках игральной кости 3 очка выпадут ровно 2 раза?
Решение.
п=10, т=2, ![]() ,
, ![]() и
и
![]()
Задача
В части А Единого государственного экзамена по математике в 2007 году
было 10 заданий с выбором ответа. К каждому из них предлагается 4 варианта
ответа, из которых только 1 верный. Если ученик не знает предмет и отвечает
наугад, то с вероятностью ![]() он выберет
правильный ответ, а с вероятностью
он выберет
правильный ответ, а с вероятностью ![]() - ошибется. Для
получения положительной оценки за экзамен необходимо правильно ответить минимум
на 6 заданий. Какова вероятность того, что нерадивый ученик сдаст экзамен?
- ошибется. Для
получения положительной оценки за экзамен необходимо правильно ответить минимум
на 6 заданий. Какова вероятность того, что нерадивый ученик сдаст экзамен?
Решение.
п=10, т=5, ![]() ,
, ![]() .
.
![]() .
.
Домашняя задача.
Стрелок стреляет в мишень. Вероятность попадания равна 0,4. Найдите вероятность того, что, сделав 5 выстрелов, он попадет в мишень не менее 2 раз.
Решение.
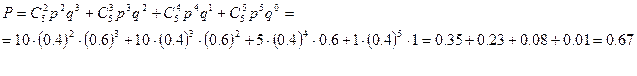
Тема: Случайные величины
Занятие 1
Распределение вероятностей случайной величины. Математическое ожидание случайной величины
Цель: изучение случайных величин
Задачи:- дать понятия: случайная величина, распределение случайной величины;
- учить приводить примеры случайных величин;
- учить составлять таблицы распределения случайной величины;
- развивать логическое мышление, кругозор, математическую речь, интерес к математике.
Ход занятия
1. Распределение вероятностей случайной величины
Случайная величина – это величина, значение которой зависит от случая. В ходе некоторого случайного опыта или наблюдения величина применяет то или иное значение. Рассмотрим следующие примеры.
1. Наблюдая движение городского транспорта, замечаем, что число машин, проезжающих за один час через не6который перекресток, под влиянием случайных обстоятельств меняется в течении суток.
2. Рост наудачу выбранного человека можно рассматривать как случайную величину, измеряя его, например в сантиметрах.
3. Срок службы телевизора или стиральной машины – величина случайная. Срок службы отсчитывается в днях от момента выпуска или продажи. Свойства этой случайной величины важны, например, при установлении гарантийного периода на новый прибор.
Эти примеры отличаются по конкретному содержанию, но у них есть общие черты.
1) В каждом примере речь идет о величине, которая характеризует некоторое случайное событие.
2) Каждая из этих величин может принимать переменное числовое значение в зависимости от случайного исхода испытания.
Случайная величина возникает как результат случайного опыта. Предположим, что случайная величина Х в некотором опыте может принимать несколько значений. Чтобы полностью описать случайную величину Х, надо указать, с какими вероятностями она принимает эти значения. Указать вероятность каждого значения можно с помощью таблицы, графика, диаграммы или формулы.
Пример. Игральную кость бросают дважды. Результаты элементарных событий представлены в таблице. По горизонтали указано число очков, выпавшее на первой кости, по вертикали – на второй.
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
1; 1 |
1; 2 |
1; 3 |
1; 4 |
1; 5 |
1; 6 |
|
2 |
2; 1 |
2; 2 |
2; 3 |
2; 4 |
2; 5 |
2; 6 |
|
3 |
3; 1 |
3; 2 |
3; 3 |
3; 4 |
3; 5 |
3; 6 |
|
4 |
4; 1 |
4; 2 |
4; 3 |
4; 4 |
4; 5 |
4; 6 |
|
5 |
5; 1 |
5; 2 |
5; 3 |
5; 4 |
5; 5 |
5; 6 |
|
6 |
6; 1 |
6; 2 |
6; 3 |
6; 4 |
6; 5 |
6; 6 |
Сумма выпавших очков – случайная величина. Возможные значения этой суммы – натуральные числа от 2 до 12. составим таблицу распределения вероятностей случайной величины.
|
Сумма очков |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Вероятность |
|
|
|
|
|
|
|
|
|
|
|
Эта информация называется законом распределения случайной величины. Закон распределения можно задавать разными способами. Основное свойство распределения заключается в том, что сумма всех вероятностей равна 1. Объясняется это тем, что сумма вероятностей значений случайной величины равна сумме вероятностей всех элементарных событий эксперимента.
Такие случайные величины, принимающие только отдельные друг от друга значения, которые можно заранее перечислить, называются дискретными случайными величинами.
В природе значения многих случайных величин изменяются непрерывно. Например, время безотказной работы прибора или изделия (телевизора, автомобиля или стиральной машины) может оказаться любым (положительным) числом. Такие случайные величины называются непрерывными.
Вернемся к формуле Бернулли ![]() .
.
Пусть случайная величина S – число успехов в серии из n
испытаний Бернулли. S может принимать значения от 0
до n. Тогда событие ![]() состоит
в том, что в результате серии испытаний наступило k
успехов. Формула дает распределение случайной величины S. Это
так называемое биномиальное распределение вероятностей, или распределение
Бернулли.
состоит
в том, что в результате серии испытаний наступило k
успехов. Формула дает распределение случайной величины S. Это
так называемое биномиальное распределение вероятностей, или распределение
Бернулли.
Пример. Таблица распределения Бернулли для n=16 при p=0,5.
|
k |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
p |
0 |
0 |
0.002 |
0.009 |
0.028 |
0.067 |
0.122 |
0.175 |
|
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
0.196 |
0.175 |
0.122 |
0.067 |
0.028 |
0.009 |
0.002 |
0 |
0 |
Как видно из таблицы, распределение вероятностей симметрично относительно значения 0,196. Это объясняется тем, что вероятности успеха и неудачи одинаковы: p=q=0,5.
Задача
В таблице дано распределение вероятностей некоторой случайной величины. Одна из вероятностей неизвестна. Найдите ее.
|
Значение |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
Вероятность |
0,05 |
0,08 |
0,2 |
|
0,2 |
0,08 |
0,05 |
Решение
1-0,05-0,08-0,2-0,2-0,08-0,05=0,34
2. Математическое ожидание случайной величины
Задача
Выпущено 100 лотерейных билетов. 40 билетов принесут их владельцам по 100 р., 10 билетов – по 500 р., 5 билетов – по 1000 р. Остальные билеты безвыигрышные. Какой средний выигрыш соответствует одному билету?
Выигрыш является случайной величиной, которая может принять значения 0, 100, 500, 1000 с вероятностями соответственно 0,45, 0,4, 0,1, 0,05. Распределение этой случайной величины можно представить таблицей:
|
Выигрыш |
0 |
100 |
500 |
1000 |
|
Вероятность |
0,45 |
0,4 |
0,1 |
0,05 |
Если покупатель приобрел бы все 100 билетов, то:
0 р. он выиграл бы 45 раз,
100 р. он выиграл бы 40 раз,
500 р. он выиграл бы 10 раз,
1000 р. он выиграл бы 5 раз.
Всего ![]() рублей.
рублей.
Выигрыш, соответствующий одному билету, в 100
раз меньше, он равен: ![]() (р.).
(р.).
Для того, чтобы лотерея приносила доход своим устроителям, цена билета должна быть больше, чем средний выигрыш. Предположим, что билет будет стоить 150 р. Все билеты будут проданы за 15000 р., на выплату выигрышей будет потрачено 14000 р., таким образом, доход от лотереи составит 1000 р. Так устроены все лотереи: среднее значение выигрыша на один билет меньше цены этого билета.
Рассмотрим общий случай. Пусть Х – случайная величина. Распределение вероятностей случайной величины Х задано таблицей:
|
Значение |
|
|
|
… |
|
|
Вероятность |
|
|
|
… |
|
Математическим ожиданием случайной величины Х называют число
![]()
Математическое ожидание называют также ожидаемым значением случайной величины Х, средним значением случайной величины.
Свойства математического ожидания.
1. Математическое ожидание постоянной равно самой постоянной: М(С)=С.
2. Постоянный множитель можно вынести за знак математического ожидания: М(СХ)=СМ(Х).
3. Математическое
ожидание суммы случайных величин равно сумме их математических ожиданий: ![]() .
.
4. Математическое
ожидание произведения независимых случайных величин равно произведению их
математических ожиданий: ![]() .
.
Задача
В таблице дано распределение случайной величины Х. найдите математическое ожидание этой величины.
|
Значение |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
|
Вероятность |
0,03 |
0,1 |
0,13 |
0,18 |
0,04 |
0,14 |
0,19 |
0,12 |
0,07 |
а)
![]()
|
Значение |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
|
Вероятность |
0,02 |
0,03 |
0,1 |
0,15 |
0,4 |
0,15 |
0,1 |
0,03 |
0,02 |
б)
![]()
Домашняя работа
Составить таблицу распределения случайной величины и найти ее математическое ожидание.
Занятие 2
Рассеивание значений. Дисперсия и стандартное отклонение. Закон больших чисел
Цель: изучение случайных величин
Задачи:- ввести понятия: дисперсия, стандартное отклонение, закон больших чисел;
- учить вычислять дисперсию, используя ее свойства;
- учить решать задачи на закон больших чисел;
- развивать логическое мышление, кругозор, математическую речь, интерес к математике.
Ход занятия
1. Рассеивание значений. Дисперсия и стандартное отклонение
Вычислим математическое ожидание случайной величины Х:
|
Значение |
2 |
20 |
28 |
50 |
|
Вероятность |
|
|
|
|
М(Х)=25.
А теперь вычислим математическое ожидание случайной величины Y:
|
Значение |
23 |
25 |
26 |
|
Вероятность |
|
|
|
М(Y)=25.
Любопытно, распределение случайных величин Х и Y разные, а математические ожидания одинаковые. Таблицы показывают, что возможные значения величины Х значительно отличаются от ее среднего значения, равного 25, в то время как значения величины Y близки к среднему значению, то есть значения случайной величины Y компактнее сосредоточены около М(Y), чем значения случайной величины Х около М(Х).
Для измерения сосредоточенности значений случайной величины обычно
применяют математическое ожидание случайной величины ![]() .
Такое математическое ожидание называют дисперсией случайной величины Х и
обозначают D(X).
Таким образом,
.
Такое математическое ожидание называют дисперсией случайной величины Х и
обозначают D(X).
Таким образом, ![]() .
.
У дисперсии также есть и недостаток: дисперсия измеряется не в тех единицах, что сама случайная величина. Например, напряжение измеряется в вольтах. Тогда дисперсию придется измерять в квадратных вольтах.
По этой причине вместо дисперсии часто используется мера рассеивания,
которая называется средним квадратическим или стандартным отклонением и равна
арифметическому квадратному корню из дисперсии, ![]() .
.
Свойства дисперсии
Дисперсия вычисляется по формуле ![]() .
.

учитывая, что ![]() ,
, ![]() и
и
![]() - постоянные числа.
- постоянные числа.
Мы получили еще одну формулу дисперсии
![]() .
.
1) Дисперсия постоянной величины равна нулю:
![]() .
.
2) Постоянный множитель можно вынести за знак дисперсии:
D(СХ)=СD(Х).
3) Дисперсия суммы независимых событий равна сумме их дисперсий:
![]() .
.
Пример. Найти дисперсию случайной величины, распределенной по биномиальному закону.
Решение. Случайная величина Х, распределенная по биномиальному закону, представляет нам число событий А при n независимых испытаниях, когда вероятность появления событий А есть p, а непоявления q=1-p.
Пусть ![]() - число событий А при i-м испытании.
- число событий А при i-м испытании. ![]() может принимать
два значения: 1 с вероятность p (А
произошло) и 0 с вероятность q (А не
произошло). Тогда
может принимать
два значения: 1 с вероятность p (А
произошло) и 0 с вероятность q (А не
произошло). Тогда ![]() .
.
Отсюда, ![]() .
.
Так как ![]() - независимые случайные
величины, то
- независимые случайные
величины, то
![]() .
.
Задача.
Проводится серия выстрелов по мишени. Вероятность попадания равна p=0,3. Подсчитывается число попаданий S. Найдите дисперсию величины S, если всего произведено:
а) 100 выстрелов;
б) 2500 выстрелов.
Решение.
а) ![]()
б) ![]()
2. Закон больших чисел
Закон больших чисел – название собирательное. Так называют математические теоремы, которые при разных условиях утверждают, что среднее арифметическое, составленное из большого числа случайных слагаемых, мало отличается от математического ожидания этого среднего арифметического. В качестве примера закона больших чисел приведем следующее утверждение.
Пусть ![]() - независимые случайные
величины, имеющие одинаковое распределение, и пусть а – общее для всех
них математическое ожидание. Тогда при достаточно больших n выполняется равенство
- независимые случайные
величины, имеющие одинаковое распределение, и пусть а – общее для всех
них математическое ожидание. Тогда при достаточно больших n выполняется равенство ![]() .
Это приближенное равенство тем точнее, чем больше n.
.
Это приближенное равенство тем точнее, чем больше n.
При больших значениях n
дисперсия среднего арифметического, которое тоже является случайной величиной,
мала, поэтому эта случайная величина не может сильно отличаться от своего
математического ожидания, то есть от а. Чем меньше дисперсия, тем меньше
случайный разброс около ожидаемого значения, то есть меньше вероятность
большого отклонения от ожидаемого значения. Другими словами, чем больше n, тем меньше значения случайной величины ![]() отличаются от а.
отличаются от а.
Закон больших чисел позволяет нам вместо математического ожидания с большой точностью использовать средние значения, полученные в результате измерения и наблюдения. Если мы провели достаточно много наблюдений случайной величины, то можем найти среднее арифметическое полученной выборки, то есть среднее выборочное.
Средне выборочное используется как приближенное значение математического ожидания.
Пример. Мы не знаем точно распределение, которому подчиняется размер горошин. Поэтому мы не знаем ожидаемый размер средней горошины. Но мы можем произвести много измерений и найти среднее арифметическое. Возьмем 1000 горошин какого-то определенного сорта, выращенного в определенных условиях. Измерим диаметр каждой горошины с точностью до 0,25 мм и результаты занесем в таблицу:
|
Диаметр горошины, мм |
5,5 |
6 |
6,5 |
7 |
7,5 |
8 |
8,5 |
|
Число горошин |
17 |
91 |
238 |
310 |
228 |
100 |
16 |
Среднее арифметическое равно
![]() (мм).
(мм).
Полученное среднее значение является оценкой математического ожидания случайной величины «диаметр горошины». При этом мы знаем, что чем больше измерений сделано, тем меньше дисперсия среднего арифметического, а значит, тем точность наших выводов. Таким образом, закон больших чисел дает нам уверенность в том, что диаметр 7,0025 мм очень близок к среднему диаметру всех горошин этого сорта, выращенных в сходных условиях.
Тема: Разработка проектов
Цель: развитие умения исследовать, проектировать ситуацию.
Задачи: - применять элементы теории вероятности и статистики в практических ситуациях;
- развивать логическую культуру учащихся.
Типы проектов: монопредметный, практико-ориентированный.
Проект №1
Определение цены сделки на квартиру
Задание
Определить среднюю цену спроса на однокомнатную квартиру, расположенную в г. Кунгуре. Определить верхнюю и нижнюю границу цен сделок по приобретению жилых помещений данного типа.
Ход исследования
1. Определить среднюю цену спроса на квартиру.
1.1. Путем случайной выборки из различных источников информации получить не менее 5 цифр спроса на квартиры.
1.2. Найти среднюю цену спроса (среднее арифметическое).
1.3. Найти минимальную цену спроса.
1.4. Найти медиану спроса.
2. Определить среднюю цену предложения на квартиру.
2.1. Путем случайной выборки из различных источников информации получить не менее 5 цифр предложений на квартиры.
2.2. Найти среднюю цену предложения (среднее арифметическое).
2.3. Найти максимальную цену предложения.
2.4. Найти медиану предложения.
3. Найти модуль разницы медианы цены спроса от средней цены спроса.
4. Найти модуль разницы медианы цены предложения от средней цены предложения.
5. Если отличия медианных цен спроса и предложения от их средних значений составляет не более 10%, то найти среднюю цену сделки, как половину суммы цен спроса и предложения.
6. Если отличия медианных цен спроса и предложения от их средних значений составляет более 10%, то найти коэффициент R, который рассчитывается по формуле:
 ,
,
где Zмс – значение цены, соответствующее медиане в упорядоченном ряду цен спроса;
Zмп - значение цены, соответствующее медиане в упорядоченном ряду цен предложения;
Zс, Zп – средние арифметические цен спроса и предложения.
7. Цена сделки равна половине суммы цен спроса и предложения, умноженной на коэффициент Rmu.
8. Теоретическая минимальная цена сделки равна минимальной цене спроса.
9. Теоретическая максимальная цена сделки равна максимальная цене предложения.
10. Сделать вывод.
Проект №2
Статистическое обследование фонда школьной библиотеки
Задание.
Выяснить, какая литература и в какой период учебного года читается учащимися чаще всего.
Ход исследования.
1. Выяснить общий фонд литературы школьной библиотеки; количество экземпляров методической, энциклопедической, литературы по естественным наукам, литература по техническому направлению, литература по общественным и гуманитарным наукам.
2. Составить таблицу распределения вероятности чтения книг в каждой группе.
3.
Определить среднюю читаемость книг за каждый месяц и весь
год. Результаты представить в виде графика: 
4. Подсчитать количество прочтенных книг в каждой группе за год. Найти дисперсию чтения за год в каждой группе литературы.
Вычисления производить по формуле: D(X)=npq,
где n – количество книг в группе;
p – отношение среднего количества прочтенных книг этой группы за год к количеству книг в группе.
5. Сделать вывод.
© ООО «Знанио»
С вами с 2009 года.
![]()

