Сборник научных статей V Международной научно-практической конференции 26-27 ноября 2014 года
МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение высшего образования
«Юго-Западный государственный университет»
(ЮЗГУ)
АКТУАЛЬНЫЕ ПРОБЛЕМЫ
И ПЕРСПЕКТИВЫ
ПРЕПОДАВАНИЯ МАТЕМАТИКИ
Сборник научных статей
V Международной научно-практической конференции
26-27 ноября 2014 года
Редакционная коллегия:
Е.А. Бойцова (ответственный редактор)
В.М.Буторин
В.И. Дмитриев
Г.А. Есенкова
Т.В. Шевцова
Курск 2014
УДК 378.016:51
ББК 74.58.264
А 437
Рецензент
Доктор педагогических наук, проректор по учебной работе
Курского государственного университета профессор В.А. Кудинов
Редакционная коллегия:
Е.А. Бойцова, кандидат технических наук, доцент (ответственный редактор)
В.М. Буторин, доктор физ.- мат. наук, профессор,
В.И. Дмитриев, кандидат физ.-мат.наук, с.н.с.,
Г.А. Есенкова, старший преподаватель,
Т.В. Шевцова, старший преподаватель
А437 Актуальные проблемы и перспективы преподавания математики: сборник научных статей V Международной научнопрактической конференции (26-27 ноября 2014 г.): / редкол. Е.А. Бойцова (отв.ред.) [ и др.]. Юго-Западный гос. ун-т. ЗАО «Университетская книга», Курск, 2014, 148 с.
ISBN 978-5-9908274-7-9
Сборник содержит собрание научных статей V Международной научно-практической конференции «Актуальные проблемы и перспективы преподавания математики», прошедшей в Юго-Западном государственном университете 26-27 ноября 2014 года.
Представлены статьи, посвященные вопросам теории и практики современной методики преподавания математики в учебных заведениях различного уровня, организации контроля знаний, умений и навыков, применению инновационных и информационных технологий в математическом образовании, непрерывности математического образования, математическим олимпиадам, применению математики в различных сферах человеческой деятельности.
Рекомендован специалистам, преподавателям, а также аспирантам, магистрантам и студентам старших курсов, интересующимся методикой преподавания математики и инновационными технологиями в образовании.
ISBN 978-5-9908274-7-9 УДК 378.016:51
ББК 74.58.264
© Юго-Западный государственный университет, 2014
© ЗАО «Университетская книга», 2014
3
СОДЕРЖАНИЕ
Н.В. Агеева
ПЕРСПЕКТИВЫ ПРИМЕНЕНИЯ ИНФОРМАЦИОННЫХ 6
ТЕХНОЛОГИЙ В ОБРАЗОВАТЕЛЬНОМ ПРОЦЕССЕ
Т.В. Андриянова, Е.И. Иноземцева, С.В. Рудюк 11
МЕТОДИЧЕСКИЙ МАРШРУТ КАК СРЕДСТВО
ПОВЫШЕНИЯ МОТИВАЦИИ ОБУЧАЮЩИХСЯ
НА УРОКАХ МАТЕМАТИКИ
Н.В. Басенко, С.А. Дыбленко, Е.В. Скрипкина 17
ВЛИЯНИЕ ДИСТАНЦИОННЫХ ОЛИМПИАД
НА РАЗВИТИЕ МАТЕМАТИЧЕСКОГО МЫШЛЕНИЯ
ШКОЛЬНИКОВ
Л.Л. Великович 21
ФИЗИКА И МАТЕМАТИКА В ТЕХНИЧЕСКОМ
УНИВЕРСИТЕТЕ: ВМЕСТЕ ИЛИ ВРОЗЬ
С.Н. Волкова, Е.Е. Сивак, М.И. Пашкова, Н.А. Костенко, 32
В.В. Герасимова
ВУЗ КАК ФОКУС КЛАСТЕРНОЙ СТРАТЕГИИ
ГОСУДАРСТВА ПРИ ПОДГОТОВКЕ КАДРОВ
М.Г. Гиоргадзе, Т.В. Меренкова, А.В. Ряднов 36
РОЛЬ МАТЕМАТИЧЕСКОЙ ОЛИМПИАДЫ
ПРИ ПОДГОТОВКЕ КВАЛИФИЦИРОВАННЫХ КАДРОВ
Л.А. Должикова 40
ИСПОЛЬЗОВАНИЕ ИНФОРМАЦИОННЫХ
КОМПЬЮТЕРНЫХ ТЕХНОЛОГИЙ НА УРОКАХ
МАТЕМАТИКИ
Г.А. Есенкова, Е.С. Есенкова 46
ПОВЫШЕНИЕ КАЧЕСТВА ПРОВЕРКИ ЗНАНИЙ
СТУДЕНТОВ ПО РАЗЛИЧНЫМ РАЗДЕЛАМ МАТЕМАТИКИ
4
НА ОСНОВЕ ФОРМИРОВАНИЯ СИНХРОННЫХ БЛАНКОВ
ТЕСТОВ И ОТВЕТОВ
Д.А. Жураев, Ж.Н. Жумаев 55
ПРИМЕНЕНИЕ ПРОГРАММЫ MAPLE В УРОКАХ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
С.А. Жураева, Н.Ш. Нурматова 61
ЦЕЛАЯ И ДРОБНАЯ ЧАСТЬ ЧИСЛА
Н.К. Зарубина 65
ОНЛАЙН-СЕРВИС WOLFRAM ALPHA
В ОБРАЗОВАТЕЛЬНОМ ПРОЦЕССЕ
Л.С. Крыжевич 69
ВЫЧИСЛЕНИЕ ПЛОЩАДИ ПОВЕРХНОСТИ ОБЛАКА ТОЧЕК,
ПОЛУЧЕННЫХ СКАНИРОВАНИЕМ ИССЛЕДУЕМОГО ТЕЛА
Д.А. Мелентьев, К.А. Фильчакова, Е.А. Башилова 75
ИСПОЛЬЗОВАНИЕ МЕТОДА РАЦИОНАЛИЗАЦИИ ДЛЯРЕШЕНИЯ АЛГЕБРАИЧЕСКИХ НЕРАВЕНСТВ
ПРОФИЛЬНОГО ЕГЭ ПО МАТЕМАТИКЕ
О.А. Мокеева, С.А. Мокеева 79
ПОДХОД К ОРГАНИЗАЦИИ ОБУЧЕНИЯ
СТУДЕНТОВ ЗАОЧНОЙ ФОРМЫ ПОЛУЧЕНИЯ
ОБРАЗОВАНИЯ ПРИ ИЗУЧЕНИИ
МАТЕМАТИЧЕСКИХ ДИСЦИПЛИН
О.А. Мокеева, С.А. Мокеева 85
ОРГАНИЗАЦИЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
СТУДЕНТОВ
Н. А. Моргунова, Е. Ю. Моргунова 91
РЕШЕНИЕ ЗАДАЧИ О МИНИМИЗАЦИИ ЦЕЛЕВОЙ
ФУНКЦИИ
Е.А. Осипова 96
ПРОБЛЕМА ПРЕЕМСТВЕННОСТИ ОБУЧЕНИЯ
ШКОЛЬНИКОВ В НАЧАЛЬНОЙ И ОСНОВНОЙ ШКОЛЕ
5
Н.В. Охотникова, Т.В. Шевцова 107
ИНТЕГРИРОВАННЫЕ ЗАНЯТИЯ ПО ЕСТЕСТВЕННОНАУЧНЫМ ДИСЦИПЛИНАМ:
МАТЕМАТИКА-БИОЛОГИЯ, МАТЕМАТИКА-ХИМИЯ
Е.А. Панина, А.Ф. Пихлап 113
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ КОНСПЕКТИРОВАНИЯ
А.С. Сеитова 117
ПРИЛОЖЕНИЯ ТЕОРИИ ПОВЕРХНОСТЕЙ
Л.И.Студеникина, Д.Н. Тютюнов 123
МЕЖДИСЦИПЛИНАРНЫЙ ПОДХОД В ИЗУЧЕНИИ
МАТЕМАТИЧЕСКИХ ДИСЦИПЛИН
Т.В. Тихоненко, М.В. Задорожнюк 126
ОПЫТ ПРЕПОДАВАНИЯ МАТЕМАТИКИ ПРОГРАММИСТАМ
А.В. Шалимова, Т.В. Шевцова 131
ВАРИАТИВНОСТЬ ПРИЕМОВ РЕШЕНИЯ
ГЕОМЕТРИЧЕСКИХ ЗАДАЧ КАК СРЕДСТВО
ДОСТИЖЕНИЯ КАЧЕСТВА МАТЕМАТИЧЕСКОЙ ПОДГОТОВКИ
Шевцова Т.В. 136
АУДИТОРНАЯ И САМОСТОЯТЕЛЬНАЯ РАБОТА
УЧАЩИХСЯ ПРИ ИЗУЧЕНИИ КООРДИНАТНОГО МЕТОДА В ШКОЛЕ И ВУЗЕ
С.В. Шеставина, О.А. Бредихина 142
ОСОБЕННОСТИ ПОСТРОЕНИЯ РАЗВИТЫХ,
МАТЕМАТИЗИРОВАННЫХ ТЕОРИЙ
В СОВРЕМЕННОЙ НАУКЕ
6
УДК 372.851 Н.В. Агеева
e-mail: [email protected]
Средняя общеобразовательная школа №5 г. Льгова,
Курская область
ПЕРСПЕКТИВЫ ПРИМЕНЕНИЯ ИНФОРМАЦИОННЫХ
ТЕХНОЛОГИЙ В ОБРАЗОВАТЕЛЬНОМ ПРОЦЕССЕ
В статье рассмотрены возможности и преимущества использования информационных технологий при обучении математике.
Ключевые слова: обучение математике, современные информационные технологии.
Современное информационное общество предъявляет ко всем типам образовательных учреждений новые требования к подготовке выпускников. Их выпускники должны иметь необходимые знания, умения и навыки; адаптационные, мыслительные и коммуникативные способности, а также владеть способами работы с информацией: собирать необходимые для решения имеющихся проблем факты; анализировать их, предлагать гипотезы решения проблем; обобщать факты, сопоставлять решения, устанавливать статистические закономерности, аргументировать свои выводы и применять их для решения новых проблем. В современных условиях, в образовательной деятельности важна ориентация на развитие познавательной самостоятельности учащихся, формирование умений исследовательской деятельности, индивидуализация целей образования.
Долгие годы работы в школе позволяют мне назвать ряд противоречий, которые присущи школьной практике:
• стремление личности к творчеству, оригинальности, самовыражению и обязательный единый план и режим общеобразовательной школы;
• репродуктивное восприятие материала отдельными обучающимися и необходимость творческого преобразования их деятельности;
7
• возрастающая сложность и насыщенность школьной программы, постоянно увеличивающийся уровень требований и способность ученика освоить весь объем предлагаемых ему сведений.
Решать эти проблемы старыми методами невозможно. Изменения, происходящие сегодня, определяют особенности и необходимость внесения изменений и в образовательные отношения. Одним из направлений решения названных задач является интеграция средств информационных технологий в образовательный процесс.
Методическая проблема, над которой мы работаем последнее время, - это «Информационно-коммуникационные технологии как средство активизации познавательной деятельности обучающихся». Работу, направленную на повышение качества знаний обучающихся, развития их творческих способностей, веду посредством внедрения в обучение новых информационных технологий. Применение информационных технологий на уроках и во внеурочной деятельности расширяет возможности творчества учеников, повышает их интерес к предмету. Знания усваиваются учеником благодаря его собственной деятельности, организуемой и управляемой так, чтобы ученик имел перед собою реальные ориентиры, позволяющие ему совершать все действия правильно и одновременно контролировать себя.
В структуре общего школьного и большинства направлений профессионального образования математика является одним из важнейших предметов. В то же время, математика - весьма сложный учебный предмет, так как математическими способностями обладают не многие, а обучать математической грамоте необходимо всех и ЕГЭ обязательно сдавать всем. И, наконец, ВУЗы предъявляют достаточно высокие требования к математической подготовке абитуриентов и студентов.
Говоря об актуальных проблемах и перспективах преподавания математики, нельзя не сказать, что использование ИКТ в деятельности школьных учителей математики открывает уникальные возможности активизации процессов познания, индивидуальной и коллективной когнитивной деятельности обучающихся. Математика – это один из тех предметов, в котором использование ИКТ может активизировать все виды учебной деятельности: изучение нового материала, подготовка и проверка домашнего задания, самостоятельная работа, проверочные и контрольные работы, внекласс-
8
ная работа, творческая работа. Особенно сильный эффект достигается при совмещении многофункционального потенциала математических систем, презентационных возможностей компьютерных технологий и использования информационного ресурса Интернет.
Приведу некоторые дидактические приемы, при реализации которых возможно и целесообразно применение математических систем с целью актуализации исследовательской деятельности обучаемых:
• демонстрация математических объектов (углубление понимания и развития пространственного мышления);
• проверка решения, полученного обычным способом, и его графическая иллюстрация; одновременно показ различных (численных, аналитических или графических) способов решения;
• проведение дополнительного исследования по решению, полученному традиционным путем (развитие исследовательскоэвристических навыков и интуиции);
• построение алгоритма действий и реализация этого алгоритма (формирование и развитие алгоритмического мышления);
• создание проблемной ситуации методом демонстрации, затем поиск способа решения (эмпирическая эвристика, когнитивность и рефлексия);
• коллективное решение большой практической задачи на основе создаваемой математической модели, реализуемой с помощью системы (задача-практикум в форме протяженного домашнего задания).
Рассмотрим возможности и преимущества использования информационных технологий при обучении решению уравнений и неравенств графическим методом.
Уравнения, неравенства и их системы, требующие нестандартного подхода к решению (например, с параметрами), зачастую включаются в содержание ЕГЭ и олимпиад. Их решения аналитически приводит к громоздким и трудным вычислениям. Одним из эффективных методов в этом случае является графический метод. Однако внимание этому методу в школьной практике обучения уделяется немного, и чаще всего он рассматривается на немногочисленных факультативных занятиях. Это связано с тем, что построение графиков функций – трудоемкий процесс, требующий много времени.
9
Таким образом, возникает противоречие между необходимостью обучения школьников графическому методу и недостатком учебного времени для качественной организации этого процесса. Использование компьютерной графики снимает эту проблему. Умение «видеть» графики, использовать их при решении уравнений и неравенств, при исследовании свойств функций является важным элементом математического образования. Возможность представления учебной информации в виде динамической графической формы является качественно новым уровнем развития традиционного дидактического принципа наглядности. В последнее время ширится признание того, что пространственное мышление играет важную роль в овладении математикой. Использование компьютера позволяет сместить акцент в школьной практике в сторону процессов, основанных на зрительной переработке информации.
Проблема наглядности - одна из основных проблем и при изучении геометрии в школе. Многие свойства геометрических фигур становятся очевидными, если рассматривать не статические фигуры, а наблюдать, что происходит с ними при изменении размеров и форм, а затем проводить исследования и делать интересные выводы. Современная трехмерная графика позволяет создавать модели сложных геометрических тел и их комбинаций, вращать их на экране, менять освещенность, что повышает уровень мотивации учащихся к изучению данного предмета.
Одним из направлений компьютеризации российской системы образования является постепенный переход от традиционных форм контроля и оценивания знаний к компьютерному тестированию с использованием разнообразных программных средств. В настоящее время существуют различные многофункциональные пакеты, позволяющие не только проводить проверку уровня знаний, но и оценивать результаты тестирования, организовывать помощь школьникам, осуществляя функцию репетитора. Таким образом, использование компьютера в качестве средства контроля позволяет интенсифицировать образовательный процесс, активизировать познавательную деятельность, повысить эффективность контроля знаний обучающихся.
Современные тенденции таковы, что традиционная методика обучения математике в школе во все большей степени будет опираться на использование программных средств, ознакомление уча-
10
щихся с методами применения математических систем на регулярной основе, которое станет частью обязательного образования.
Такое расширение инструментария математики и информатики в школьном математическом образовании станет эффективным способом воплощения деятельностного подхода к обучению, расширения понимания учащимися роли математики как средства решения практических задач, а в итоге - усиления прикладного компонента качества математического образования, соответствия его требованиям Федерального образовательного стандарта второго поколения.
N.V. Ageeva
e-mail: [email protected]
Secondary school №5, Lgov, Kursk region
PROSPECTS FOR THE APPLICATION OF INFORMATION
TECHNOLOGY IN THE EDUCATIONAL PROCESS
The article describes the features and benefits of using information technology in teaching mathematics.
Key words: teaching mathematics, modern information technology.
Список литературы
1. Селевко Г.К. Педагогические технологии на основе информационно-коммуникационных средств. //Москва: НИИ школьных технологий, 2005. С. 54 - 112.
2. Гилярова М. Г. Использование информационных технологий для реализации наглядности как одного из важнейших принципов обучения математике // Информатика и образование. 2008. № 11.
3. Федеральный государственный образовательный стандарт среднего (полного) общего образования / М-во образования и науки РФ. М.: Просвещение, 2013.
11
УДК 372.851
Т.В. Андриянова, Е.И. Иноземцева, С.В. Рудюк e-mail: [email protected]
Муниципальное бюджетное нетиповое общеобразовательное
учреждение «Городской классический лицей», Кемерово
МЕТОДИЧЕСКИЙ МАРШРУТ КАК СРЕДСТВО
ПОВЫШЕНИЯ МОТИВАЦИИ ОБУЧАЮЩИХСЯ
НА УРОКАХ МАТЕМАТИКИ
В статье рассматривается роль методического маршрута уроков математики.
Ключевые слова: методический маршрут, сервисы Web 2.0, мотивация, рефлексия, Google-таблицы, преобразование графиков.
Основные задачи современного образования направлены на формирование всесторонне развитой личности, подготовленной к воспроизведению (сохранению) и развитию материальной и духовной культуры общества, умений и желания обучающихся учиться всю жизнь, работать в команде, способности к саморазвитию на основе рефлексивной самоорганизации.
Для реализации этих задач каждый учитель должен стать новатором, найти свою методику, отвечающую его личностным качествам, поскольку без этого, всё остальное может остаться лишь формальным и дорогостоящим нововведением, которое так и не «дойдет до живого дела».
Одним из возможных направлений работы учителя, может стать разработка им методического маршрута, обеспечивающего новое качество образования.
Методический маршрут - это описанный педагогом по определенному плану инновационный педагогический опыт, изучая который, коллеги могут повышать свою профессиональную компетентность.
Ведущая педагогическая идея опыта заключается в создании необходимых условий:
- для формирования устойчивой, положительной мотивации обучающихся, развитие интереса к предмету через организацию
12
активного обучения, их индивидуального развития, повышения познавательной активности через широкое применение на уроках математики современных образовательных технологий;
- для возможности творческого разнообразия форм и методов деятельности учителя в целях интенсификации учебнопознавательной деятельности обучающихся.
Доступность педагогического опыта позволила нам разработать методический маршрут «Преобразование графиков квадратичной функции» и внедрить его на урок математики в 8 классе. Маршрут разработан на основе личностноориентированного подхода, который направлен на личность обучающегося и его максимальное развитие, включает в себя исследовательский и проблемный методы, рефлексию.
В содержание методического маршрута вошли уроки математики по теме «Построение и преобразование графиков функций», имеющих общую содержательную линию и дидактическую цель, направленную на формирование личностных, предметных и метапредметных результатов. “Фишка” методического маршрута заключается в организации исследовательской деятельности с помощью сервисов Web 2.0, с целью изменить роль обучающегося в учебном процессе от пассивного наблюдателя до активного исследователя. Уроки проводятся с использованием электронных Google Docs и Google forms, интерактивной и стикерной досок.
Основной задачей данной работы является обобщение знаний по темам: «Выделение полного квадрата в квадратном трехчлене», «График квадратичной функции», «Построение и преобразование графиков функций». Наглядная демонстрация обучающимся возможностей использования электронных таблиц для самоконтроля, изучения свойств функций, построения графиков произвольных функций и т.д., позволяет повысить их познавательную активность и оценить практическую значимость изучаемого учебного материала, сформулировать алгоритмы преобразований графиков функций.
Основными видами деятельности обучающихся на уроке являлись следующие:
- работа в группах (работа в сервисе Web 2.0, linoit.com);
13
- дискуссия (обсуждение результатов работы, формулировка алгоритмов преобразования графиков произвольной функции);
- индивидуальная работа;
- практическая деятельность (совместное построение графика функции, включающего в себя все преобразования);
- рефлексия обучающихся (оценка результативности урока с использованием анкеты);
- рефлексия учителя (оценка работы на уроке).
Предложенные в данном методическом маршруте приемы и методы могут быть применены для целого ряда тем учебного плана по математике в 10-11 классах, таких как «Построение графиков тригонометрических, показательных, логарифмических функций», «Преобразование графиков функций» и др.
Ключевой идеей уроков является получение экспериментальным путем алгоритмов построения графиков функций вида y ax m2, y ax2 n, y ax m2 n, если известен график функции y ax2 , и применение полученных алгоритмов к преобразованию графиков произвольных функций.
Проведение таких уроков предполагает использования компьютерного класса или мобильного компьютерного класса. В ходе работы на уроках формируются важные умения, связанные с представлением, анализом и интерпретацией данных.
Совместное использование Google-таблиц для протоколирования результатов опытов и автоматизация расчетов и построения графиков показывает обучающимся реальные подходы к использованию средств информационно-коммуникационных технологий для оптимизации деятельности, связанной с обработкой статистических массивов информации.
Приведем пример урока математики в 8 классе с использованием методического маршрута по теме:
«Преобразование графиков квадратичной функции».
I. Этап самоопределения к деятельности
Сегодня мы сформулируем алгоритмы построения графиков следующих функций y ax m2, y ax2 n, y ax m2 n, если известен график функции y ax2 ,
II. Этап актуализации знаний и фиксации затруднений в деятельности
14
Для этого устно ответим навопросы:
- Как называют график функции y ax2?
- Что нам известно о коэффициенте a?
- Где расположена вершина параболы?
- Какова формула для ее вычисления?
- Что является осью симметрии параболы?
- Куда направлены ветви параболы? От чего это зависит?
- Как можно построить график функции y 2x 12 3?
III. Этап построения проекта выхода из затруднений и обобщения затруднений во внешней речи
Учитель рассматривает пример на построение графиков функций с помощью Google – таблиц.
ПРИМЕР. (Используется при объяснении материала через проектор или интерактивную доску).
Построить графики функций y1 ax2и y2 ax3 на интервале
[- 3; 3] шагом 0,5.
Алгоритм выполнения задания: открыть Google – таблицу, заполнить таблицу значений. Выделить таблицу и указать тип диаграммы – линия. Выбрать формат диаграммы - гладкий график. В макете указать название диаграммы «Графики», дать название осей: X и Y. Должен получиться график.
Групповая работа
Класс делится на 4 группы. Каждая группа получает задания для работы.
Группа 1
Построить графики функций y1 x2, y2 x2 1, y3 x2 1 на интервале [- 3; 3] с шагом 0,5.
Группа 2
Построить графики функций y1 x2, y2 x 12, y3 x 12 на интервале [- 3; 3] с шагом 0,5.
Группа 3
Построить графики функций y1 2x2, y2 2x2 1, y3 2x2 1 на интервале [- 3; 3] с шагом 0,5.
15
Группа 4
Построить графики функции y1 x2, y2 x 12 3, y3 x 12 3 на интервале [- 3; 3] с шагом 0,5.
Далее, группы выполняют задания и обсуждают результаты работы в группах и между группами, отвечая на вопросы:
- Как получается график функции y x m2 из графика y1 ax2?
- Как получается график функции y ax2 n из графика y1 ax2?
Как получается график функции y ax m2 n из графика y1 ax2?
Результаты оформляются на стикерной доске (сервис linoit.com).
IV. Этап самостоятельной работы
Учитель обобщает, полученные результаты для случая f (x) ax m2 n и предлагает использовать данные графики в упражнении “Зонтик” (строятся в одной системе координат на отрезке 4 графика квадратичной функции, при правильном построении получается зонтик).
V. Рефлексия и оценка работы деятельности
Выполняется с помощью “карты успеха” (таблица, в которой указываются критерии выставления баллов за каждое упражнение).
В конце уроков обучающиеся анализируют свою работу, отвечая на вопросы анкеты:
- На уроке я работал активно (пассивно)?
- Своей работой на уроке я доволен (недоволен)?
- Урок мне показался коротким (длинным)?
- За урок я не устал (устал)?
- Материал урока мне был понятен (не понятен), интересен (скучен)?
VI. Домашнее задание
Задается с учетом результатов работы на уроке.
16
Результаты и активность обучающихся на таких уроках подтверждают, что использование методического маршрута является одним из лучших средств повышения мотивации обучающихся, способствует развитию их личности, формированию гражданской идентичности, помогает учителю отследить ценностные ориентиры, которые встраиваются в новое поколение стандартов российского образования, обеспечивая комфортную рабочую обстановку на уроке.
__________________
1. Андреева В. А. Использование сервисов Web 2.0 для организации совместной работы на уроках https://docs.google.com/document/d/1E6gx2BT40qDKCtfaEAph-
6nmcMIZFFleYDjjS7moxXg/edit
2. Брыксина О.Ф., Круподерова Е. П., Пирог Т. Г., Пособие для разработчиков методических маршрутов. Онлайн курс Intel
Teach - (ITAO). Концепция Методического маршрута. 2013.docx
T.V. Andriyanova, E.I. Inozemtsva, S.V. Rudiuk e-mail: [email protected]
Municipal budget non-standard educational institutions “Municipal classical lyceum” in Kemerovo
THE METHODICAL ROUTE AS THE WAY TO RAISE
THE STUDENTS MOTIVATION AT THE LESSONS OF MATH
This article is about the role of methodical route at the lessons of math.
Key words: methodical route, Internet services Web 2.0, motivation, Google-charts, diagram transformation, feedback.
17
УДК 37.041
Н.В. Басенко1, С.А. Дыбленко2, Е.В. Скрипкина3 e-mail: [email protected]
1,2
Лицей №6 им. М.А. Булатова, Курск
3
Юго-Западный государственный университет, Курск
ВЛИЯНИЕ ДИСТАНЦИОННЫХ ОЛИМПИАД
НА РАЗВИТИЕ МАТЕМАТИЧЕСКОГО МЫШЛЕНИЯ
ШКОЛЬНИКОВ
Рассмотрено применение интернет – ресурсов с целью повышения интереса к обучению математики. Приведен перечень олимпиад и дистанционных математических школ, где любой обучающийся может проявить свои математические способности.
Ключевые слова: интернет-кружок МетаШколы, Центр развития мышления и интеллекта, олимпиада "Сократ".
Создание условий, обеспечивающих выявление и развитие талантливых детей, реализацию их возможностей, является одной из приоритетных задач современного общества. В национальной инициативе «Наша новая школа» это направление определяется как ключевое в развитии общего образования.
Ежегодно школьники принимают участие во Всероссийских предметных олимпиадах, успешно занимаются в различных научных обществах («Шаг в будущее», «Юниор», «Харитоновские чтения»). Однако все эти олимпиады и конкурсы нацелены на то, чтобы из учеников выделить самых способных и одаренных. Роль таких олимпиад огромна, но подавляющее большинство школьников остается в стороне от них.
В век развития компьютерных технологий главной задачей учителей и преподавателей, является научить школьника использовать компьютер для самообразования.
За последнее время преподавание математики подверглось перестроению. Математика и ее значение в жизни общества растет с каждым днем. В нашей стране большое значение придается именно математическому образованию. Развитию математического мышления помогает ряд интернет – мероприятий. В настоящее время
18
сами родители и педагоги могут помочь своему ребенку, не покидая родного дома, включиться в олимпиадное движение в Интернете. Наиболее известными, получившими широкое распространение среди школьников, являются интернет-кружок МетаШколы и Центр развития мышления и интеллекта (Центр РМИ).
Интернет-кружок МетаШколы (Санкт – Петербург) существует уже пять лет. Работа кружка ориентирована на решение нестандартных математических задач и задач повышенной сложности для
учеников 3-8 классов. Содержание задач отвечает школьной программе. Ведет занятия учитель математики физикоматематического лицея №366 Санкт-Петербурга Е.В. Смыкалова, автор пособий по математике, кандидат педагогических наук.
Достоинство этого кружка в том, что, не выходя из дома, можно получить серьезную математическую подготовку, которая позволяет с успехом участвовать в олимпиадах разного уровня. Участники кружка могут выйти через Интернет на связь с руководителем и выяснить все неясные вопросы. Занятия проходят в увлекательной форме, при этом степень сложности заданий возрастает по мере обучения. Три раза в год для всех учеников проводятся Всероссийские Интернет – олимпиады. Результатом этих олимпиад является не только удовольствие от решения интересных задач, но и дипломы особого образца.
Центр развития мышления и интеллекта (Центр РМИ) так же проводит предметные олимпиады и конкурсы по самым разнообразным тематикам, направленным на достижение поставленных целей и выполнению задач. Своими основными задачами Центр ставит следующие:
1. Стимулирование развития мышления и интеллекта участников дистанционных мероприятий;
2. Развитие интереса участников к познавательной деятельности;
3. Развитие навыков участников по эффективному поиску, структурированию и качественной обработке информации для получения необходимого результата.
В конкурсах и олимпиадах могут участвовать как педагоги со своими учащимися, так и сами ученики. Для этого предусмотрена регистрация и подачи заявки отдельно для учителей и для учени-
19
ков, которые проявили инициативу самостоятельно участвовать в мероприятиях. Тематика проводимых конкурсов разнообразна. Процедура регистрации, создание личного кабинета учителя или ученика и подача заявки на участие в олимпиаде или конкурсе подробно описана на сайте www.vot-zadachka.ru в разделах «Регистрация» и «Личный кабинет».
Центр РМИ проводит конкурсы и олимпиады для учащихся 1-11-х классов всех форм обучения, охватывая тем самым все возрастные категории. Все задания мероприятий составляются и проверяются компетентным жюри. Недостатком работы центра является то, что олимпиады не входят в «Перечень олимпиад школьников», утверждаемый Министерством образования и науки РФ. Однако конкурсы и олимпиады позволяют участникам развить полезные навыки, получить знания, освоить новые технологии, а также научиться продуктивно и конструктивно мыслить. Победители получают дипломы, а учителя получают сертификат куратора.
Широко известна среди школьников так же интернет - олимпиада "Сократ", потому что олимпиадные задания оформлены в виде игры с определением рейтинга, набором очков и баллов. Ее качественное отличие от других олимпиад заключается в том, что решённые задачи сохраняются на сервере.
Что представляет собой тур на олимпиаде «Сократ»? Длительность тура математической олимпиады может составлять от одного до полутора месяцев. Место в рейтинге будет определено по итогам всех игр, сыгранных участниками олимпиады. Когда тур олимпиады будет завершён, все участники олимпиады снова становятся совершенно равными, достижения остаются в предыдущем туре.
Математическая интернет – олимпиада «Сократ» для школьников имеет определённые правила. К примеру: в олимпиаде могут принимать участия только ученики 5-8 классов; школьники обязаны знать русский язык и иметь свободный выход в сеть Интернет; участие родителей и учителей приветствуется. Поговорив с ребенком, посмотрев "Олимпиадную книгу", разделы сайта: "Логические задачи", "Прохождение конкурса", всегда возможно выбрать в Каталоге нужный конкурс. Оформление заказа начинается на страничке выбранного конкурса. За символическую плату (40 – 50 руб.) во время конкурса участник проходит две тренировочных игры, два
20
Детских Форума, и один итоговый конкурс. Результаты конкурса показываются на сайте в пяти номинациях. Информация о каждом участнике может быть занесена в Книгу Олимпиадников.
Нельзя также забывать и об игре «Кенгуру – математика для всех», которая известна и любима многими школьниками.
Создание условий, индивидуальные образовательные маршруты, построенные в совместной деятельности всех участников образовательного процесса – учеников, родителей и педагогов - способствуют формированию ключевых компетенций обучающихся. Среда, созданная педагогами школы совместно с интернет – структурами, позволяет раскрывать и реализовывать свои способности, свои таланты в жизни каждому ученику.
__________________________________
1. Березовин Н.А., Сманцер А.Л. Воспитание у школьников интереса к учению. Минск: Народная асвета, 1987. 74 с.
2. Основы педагогического мастерства. Под ред. И. А. Зязюна. Киев: Вища школа. Изд-во при Киев. ун-те, 1987. 200 с.
N.V.Basenko1, S.A.Dyblenko2, E.V.Skripkina3 e-mail: [email protected]
1,2
Bulatov Lyceum №6, Kursk
3
Southwest State University, Kursk,
INFLUENCE DISTATSIONNYH CONTEST'S DEVELOPMENT
OF MATHEMATICAL THINKING PUPILS
The application of the Internet - resources in order to increase interest in learning mathematics. A list of competitions and remote mathematical schools where every student can demonstrate their mathematical abilities.
Key words: Internet circle MetaShkoly, Development Center of thinking and intelligence, Olympiad , "Socrates ."
21
УДК 378.147:51
Л. Л. Великович
e-mail: [email protected]
Гомельский государственный технический университет имени
П.О. Сухого, Республика Беларусь
ФИЗИКА И МАТЕМАТИКА В ТЕХНИЧЕСКОМ
УНИВЕРСИТЕТЕ: ВМЕСТЕ ИЛИ ВРОЗЬ
В статье обсуждаются проблемы взаимодействия курса физики и математики технического университета – то, что в школе принято называть межпредметными связями. Приводится авторская схема процесса познания физики. Утверждается, что преподавание физики также должно осуществляться по этой схеме. Обсуждаются пути и способы добычи информации в физике с помощью математики и обратная связь. А также многочисленные педагогические проблемы, включая теорию неявных знаний.
Ключевые слова: математика, физика, информация, теория, задача, логическая цепочка, метод.
Математику часто называют языком науки или, по крайней мере, языком естественных наук, и это справедливо: законы физического мира намного точнее выражаются при помощи математических уравнений, чем будучи записаны или произнесены словами. И это еще не все. Шинтан Яу
Настоящая статья является продолжением исследований, начатых в [1]. Приведем основные идеи из этой работы, дополненные новыми мыслями.
Процесс познания в физике
Физика, математика и информатика, несомненно, составляют фундамент современного инженерного образования, причем особая роль в этой троице принадлежит физике, по законам которой функционируют все технические системы (именно это наблюдение подтолкнуло в свое время Г. С. Альтшуллера к созданию ТРИЗ [2]).
22
Общеизвестно, что математика – это язык и инструмент, без которого не может обойтись ни одна физическая теория. В подтверждение приведем схему, по которой осуществляется типичный процесс познания в физике (рис. 1):
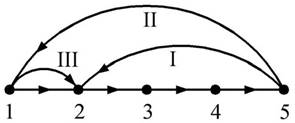
Рис. 1. Процесс познания в физике
1 – реальная физическая ситуация; 2 – модельная физическая ситуация; 3 – математическая модель; 4 – математическая информация; 5 – физическая интерпретация (информация); I – проверка на модельную адекватность; II – проверка на реальную адекватность; III – преобразование модели (в случае необходимости)
Два примера физического моделирования
Пример 1. Кинетическая теория (J. B. Marion) [3]
При выводе микроскопического уравнения состояния идеального газа руководствуются следующими допущениями:
1)газ состоит из большого числа молекул, размеры которых ничтожны по сравнению со средним расстоянием между ними;
2)на молекулы не действуют никакие силы, за исключением тех моментов, когда они сталкиваются со стенками сосуда, т. е. между молекулами нет взаимодействия;
3)движение молекул происходит совершенно хаотично;
4)движение молекул подчиняется законам Ньютона;
5)соударения молекул сотстенками сосуда являются упругими.
Замечательно, что столь простая классическая модель идеального газа позволяет получить уравнение состояния, которое очень хорошо описывает поведение реальных газов. Это тем более замечательно, если вспомнить, что теоретические допущения являются
23
всего лишь приближением к физической реальности. На самом деле молекулы в газе взаимодействуют друг с другом и имеют конечные размеры. Учесть эти обстоятельства удалось в более точной теории, которая дает нам независимый способ определения размеров молекул (~10-8 см) и характера их взаимодействий. Для уточнения теории в нее пришлось внести изменения, учитывающие квантовые эффекты, и ныне кинетическая теория газов является одной из наиболее широко используемых (и наиболее хорошо разработанных) физических теорий.
Пример 2. Разработка нефтяных месторождений
(H.B.Crichlow) [4]
Предсказание характеристики нефтяного пласта зависит от возможности инженера прогнозировать свойства флюидов в пласте. После оценки пористости пласта и насыщенности его флюидами можно определить добывные возможности месторождения.
В экспериментах Дарси были введены следующие предположения, ограничивающие области применения закона:
1. Флюид – однородный и однофазный.
2. Отсутствуют химические реакции между средой и флюидом.
3. Проницаемость не зависит от типа флюида, температуры, давления и пространственных координат.
4. Течение считается ламинарным, т. е. отсутствует турбулентность.
5. Отсутствует электрокинетический эффект.
6. Отсутствует эффект Клинкенберга.
Пояснение. Электрокинетический эффект – разность потенциалов, возникающая при движении жидкости под давлением через пористую мембрану или капилляр. Эту величину обычно называют дзета-потенциалом.
Эффект Клинкенберга – если размер пор приближается к размеру длины свободного пробега молекул, возникает эффект прилипания частиц к стенкам.
Закон Дарси гласит: скорость фильтрации однородной жидкости в пористой среде прямо пропорциональна градиенту гидравлического давления и площади сечения, перпендикулярной к направлению потока, и обратно пропорциональна ее вязкости.
24
Примечание. А вот как выглядит в этом случае математическая модель.
![]() k
p z V
k
p z V
s s s , (1)
r
где Vs – массовая скорость в направлении потока s ; k – про-
ницаемость для однородных флюидов; μ – динамическая вязкость; p – давление; z – вертикальная координата;
1
v – удельный объем (
![]() );
ρ – плотность флюида; g –
g
);
ρ – плотность флюида; g –
g
ускорение свободного падения тела.
С помощью уравнения (1) можно определить проницаемость в пористой среде.
p z
![]() Сумма
характеризует потенциал скорости фильт-
Сумма
характеризует потенциал скорости фильт-
s s рации флюида, поэтому уравнение (1) можно записать в виде:
k
![]() Vs
s , (2)
Vs
s , (2)
где Ф – полный потенциал скорости движения флюида.
Интересная аналогия
Электролитические модели стационарных процессов разрабатывались некоторыми исследователями, такими, как Ботсет, Виков и Маскет, с целью анализа движения фронтов флюидов в пласте. Принцип действия этих моделей основан на аналогии между законом Ома для электрического тока в проводнике и законом Дарси для пористой породы.
25
Таблица 1. Аналогия между характеристиками флюидов и понятиями, принятыми в электротехнике
|
Наименование величины |
Размерность |
Наименование величины |
Размерность |
|
Давление p |
кгс/см2 |
Напряжение E |
В |
|
Добыча/закачка q |
см3/с |
Сила тока i |
А |
|
Объем флюидов (запасы) Vc |
см3
|
Емкость электрическая CE
|
мкФ
|
|
kh Проводимость |
Д см
сП |
Электрическая 1 проводимость R |
Ом |
|
Истинное время процесса t |
с |
Время моделирования t |
с |
Некоторые из педагогических проблем преподавания физики
Мы считаем, что и преподавание физики должно осуществляться в духе схемы из рис. 1. Перечислим некоторые из педагогических проблем, которые при этом возникают:
• недостаточное знание студентами школьного курса физики;
• слабая подготовка по элементарной математике;
• плохая память;
• неустойчивость внимания;
• отсутствие наблюдательности (полное или частичное);
• завышенная самооценка.
На пути взаимодействия преподавателя и студенческой аудитории лежат известные в теории коммуникаций барьеры общения. «Так, В. Шепель выделяет шесть наиболее явных барьеров: 1) дискомфорт физической среды, в условиях которой воспринимается сообщение; 2) инерция включенности, т.е. озабоченности слушателя иными проблемами; 3) антипатия к чужим мыслям, стереотипизированность сознания, амбициозность; 4) языковый барьер – существенное различие словарного запаса, лексикона коммуникатора и коммуниканта; 5) неприятие имиджа коммуникатора.
А вот еще одна классификация барьеров: а) фонетический – невыразительная быстрая или медленная речь, речь-скороговорка, акцент, речь с большим количеством звуков-паразитов и т.п.; б) се-
26
мантический – различие в системах значений слов; в) стилистический – несоответствие стиля речи коммуникатора и ситуации общения или стиля общения и психологического состояния партнера по общению; г) логический – сложная, непонятная или неправильная логика рассуждений» [5].
Но самая главная проблема состоит в том, что у большинства современных студентов уровень мотивации недостаточно высок. Причин здесь несколько. Во-первых, это только что перечисленные педпроблемы: хотим учиться, но не можем. Во-вторых, отсутствие основных навыков приобретения знаний. В-третьих (и, повидимому, это самое важное), размытость конечной цели обучения.
Универсальная схема обучения (УСО)
Что же можно противопоставить этим негативным тенденциям? Для ответа на этот вопрос приведем универсальную схему обучения (УСО):
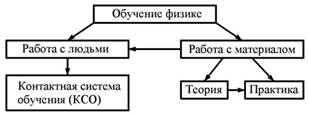
Рис. 2. Универсальная схема обучения (УСО)
Из двух составляющих УСО важнейшей является работа с людьми. Отличительные черты КСО см. в [6]. Здесь лишь напомним, что контакт – положительная эмоционально-энергетическая связь между людьми.
Теперь обсудим вторую составляющую УСО. Работа с материалом, прежде всего, предполагает его адаптацию к уровню осведомленности студенческой аудитории при сохранении информативности.
27
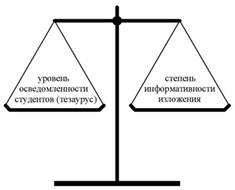
Рис. 3. Диалектическое противоречие процесса преподавания физики
Наметим один из возможных подходов к разрешению этого диалектического противоречия. Осуществляя наблюдения, проводя эксперименты (в том числе компьютерные), делая математические выкладки, создавая теории, физик-исследователь преследует, по существу, одну и ту же цель – получение информации и желательно в числовом виде. Вот что пишет по этому поводу академик А. А. Самарский [7]: «Со времен Галилея описание физического явления считается достоверным, если его факторы выражены числовыми величинами. Некоторые из этих величин удается измерить непосредственно, для определения других используются законы природы, выражающие взаимозависимости тех или иных физических факторов между собой». Соответственно, у преподавателя физики есть альтернатива выбрать тот или иной способ демонстрации процесса получения необходимой информации в зависимости от конкретной физической ситуации.
Использование математики для получения информации в физике.
Как же используется математика для получения информации в физике? Выслушаем мнение на этот счет известного советского физика-методиста П. А. Знаменского [8]: «Математическими приемами в физике пользуются весьма часто: во-первых, для выражения законов в общей и точной форме; во-вторых, для вывода тех или иных закономерностей из некоторых общих теоретических предпосылок; в-третьих, для преобразований выведенных формул в дру-
28
гие; в-четвертых, для нахождения таких величин, измерение которых непосредственно невозможно; в-пятых, при разнообразных расчетах и решении задач».
Использование физики в преподавании математики.
Скажем теперь несколько слов об обратной связи. Начиная с физической постановки соответствующих задач и заканчивая математические преобразования физической интерпретацией, мы даем студенту возможность убедиться в полезности всего происходящего для его технического будущего.
Примеры использования физики в преподавании математики.
1. Знаменитая формула конечных приращений Лагранжа
f (b) f (a) f (c)(b a), (3)
для доказательства которой он использовал прием повышения
размерности [2], с точки зрения физики вполне очевидна: пройденный путь f (b) f (a) f равен средней скорости движения f (c), умноженной на время b a t, за которое он пройден.
2. Аналогично интерпретируется и следующее утверждение. Теорема о среднем для определенного интеграла:
b
f (x)dx f (c)(b a)
(4)
a
3. Формула Остроградского-Гаусса:
P Q R
![]() V x y z dxdydz
Pdydz Qdxdz
Rdxdy
(5)
V x y z dxdydz
Pdydz Qdxdz
Rdxdy
(5)
4. Формула Остроградского-Гаусса на языке физики:
r r
divudV udr
(6)
V
29
В гидродинамике формула Остроградского-Гаусса устанавливает равносильность двух способов подсчета жидкости, вытекающей из оболочки (σ) в единицу времени:
1)исходя из производительности точечных источников, заполняющих область V (левая часть равенства);
2)исходя из скорости частиц жидкости в момент их прохождения через оболочку (σ) (правая часть равенства.)
В заключение приведем пожелания-рекомендации преподавателю физики:
1. Надо исходить из того, что студенты толком не помнят ни физики, ни математики.
2. Использовать исторические факты в процессе преподавания и другие приемы психологической разгрузки.
3. Явно осуществлять этап физического моделирования.
4. Должное внимание уделять логике рассуждений (см., например, [9]). В частности, четко отделять факты, полученные экспериментально, от фактов, выводимых из них логическим путем, в том числе применением математических методов.
5 . Главное – это физический смысл происходящего. Но очень хочется, скажем, при использовании интегрального исчисления, чтобы был показан сам процесс составления дифференциального уравнения.
Неявные знания.
Известный тезис М. Полани (M. Polanyi, 1967): «Мы знаем больше, чем можем сказать», будучи адаптированным к преподаванию, по нашему мнению, звучит так: «Мы хотели бы сказать больше, чем можем» (фактор времени и другие обстоятельства). В итоге часть связующей элементарной информации остается за кадром, а это лишает возможности недостаточно осведомленного человека воспринять картину в целом. Вопрос: что делать? Ответ: помнить об этом и руководствоваться вторым правилом Декарта: «подвергай все дроблению».
А вот что пишет об этом известный французский специалист в области искусственного интеллекта Ж.-Л. Лорьер (J.-L. Laurière): «Когда я учился в лицее, я жадно впитывал знания по физике и математике, постоянно спрашивая себя: а для чего все
30
это может пригодиться? Что касается физики, то ее отношение к реальной жизни представляется очевидным, но мы тогда не могли в это поверить, настолько все было таинственным. Физика представала перед нами как причудливая игра, в которую играют взрослые. С математикой же все было по-другому. В ней нас вдохновляла красота абстракции, мы получали удовольствие от поиска красивых доказательств. Однако ко всему этому часто примешивалось ощущение, что нас обманывают. Нам все время преподносили определения и доказательства как настоящую реальность, но причины явлений никогда не объяснялись. Казалось, что большую часть доказательств преподаватели получают с помощью магических манипуляций с кусочком мела у доски. Как можно было связать воедино все эти линии и не выпустить из поля зрения ни одну из них от самого начала доказательства до его чудесного конца? И над всем этим: «А для чего все это надо?»
Ответ на этот вопрос пришел позже, через несколько лет «активной» жизни. На самом деле все это ни для чего не было надо, потому что предметы, которые мы изучали, вносились в школьные программы произвольно. По правде говоря, они служили лишь поводом для перехода к более серьезным вещам, таким, как учиться понимать, учиться решать задачи, учиться познавать. Но любопытно, что эти «вещи» не признаются и почти не преподаются. Можно сказать, что существует определенный вид интеллектуального терроризма, когда некоторых учеников называют «нуль в математике», хотя их единственная вина состоит в том, что они не понимают то, о чем... никогда не говорится. Некоторым удается этого избежать, потому что они раньше сумели познакомиться с неявными правилами этой игры» [10].
Список литературы
1. Великович, Л. Л. Физика и математика в техническом университете: проблемы взаимодействия и применения в процессе преподавания // Физическое образование: современное состояние и перспективы: материалы Республ. науч.-метод. семинара, посвященного 65летию физ.-мат. факультета МГУ им. А. А. Кулешова, Могилёв, 16 окт. 2014 г. С. 9–12.
31
2. Альтшуллер Г.С. Творчество как точная наука. М.: Советское радио, 1976. 175 с.
3. Дж. Б. Мэрион. Физика и физический мир. М.: Изд-во «Мир», 1975. Пер. с англ. под ред. Е. М. Лейкина и С. Ю. Лукьянова. 623 с.
4. Генри Б. Кричлоу. Современная разработка нефтяных месторождений – проблемы моделирования. М.: Недра, 1979. Пер. с англ. 303 с. Пер. изд. США, 1977.
5. Основы теории коммуникации: Учебник / Под. ред. проф.
М. А. Василика. М.: Гардарики, 2003. 615 с.
6. Великович Л.Л. Математика атакует первокурсника. Подходы к решению проблемы // Актуальные проблемы и перспективы преподавания математики: сб. науч. ст. III Междунар. науч.-практ. конф. Курск, 2012. С. 114–123.
7. Самарский, А. А. Что такое вычислительный эксперимент // Что такое прикладная математика. М.: Знание, 1980, С. 22-35 (Новое в жизни, науке, технике. Сер. «Математика, кибернетика»; № 10).
8. Знаменский, П. А. Методика преподавания физики. Ленинград: УЧПЕДГИЗ, 1954. Пособие для учителей, изд. 2-е, перераб. 551
с.
9. Мелёшина, А.М., Гарунов, М. Г., Семакова, А. Г. Как изучать физико-математические дисциплины в вузе. Воронеж: Изд-во ВГУ,
1988. 208 с.
10. Лорьер Ж.-Л. Системы искусственного интеллекта. М.: Мир, 1991. Пер. с франц. 568 с.
L.L. Velikovich e-mail: [email protected]
Pavel Sukhoi State Technical University of Gomel (Republic of Belarus)
PHYSICS AND MATHEMATICS IN A TECHNICAL
UNIVERSITY: TOGETHER OR APART
The author of the article considers the problems of interaction of mathematics and physics courses in a technical university – the one known as interdisciplinary connection in school program. The author’s scheme of process of learning physics is given. It is stated that physics teaching is also to be conducted according to the scheme. The article
32
contains the discussion of the ways and methods of information mining in physics via mathematics usage and the back coupling. Also multiple pedagogical issues, including latent knowledge theory are considered.
Key words: mathematics, physics, information, theory, problem, logical chain, method.
УДК 378:37.022
С.Н. Волкова, Е.Е. Сивак, М.И. Пашкова, Н.А. Костенко, В.В. Герасимова e-mail:volkova_47@ mail.ru
Курская государственная сельскохозяйственная
академия им. проф. И.И. Иванова
ВУЗ КАК ФОКУС КЛАСТЕРНОЙ СТРАТЕГИИ
ГОСУДАРСТВА ПРИ ПОДГОТОВКЕ КАДРОВ
В статье говорится о создании кластеров на основе фундаментальных и прикладных исследований с использованием инновационных технологий, связанных с модернизацией образования.
Ключевые слова: кластер, образование, инновационные технологии, исследования, производство, бизнес, моделирование.
В связи с появившимися возможностями в реализации федеральных государственных образовательных стандартов высшего образования и среднего профессионального образования (СПО), а также школьных образовательных программ, ориентированных на углубленное изучение отдельных предметов с применением инновационных технологий теории и практики, включая дистанционное обучение на базе различных платформ и библиотек, в том числе производственных и бизнес-структур, создается пространство для организации кластеров, основанных на фундаментальных и прикладных исследованиях, навыки по которым прививаются с ранних лет развития личности.
Рассмотрим цепочку, образующую учебно-производственный кластер - новое образование, которое позволяет эффективно ис-
33
пользовать имеющиеся ресурсы с компьютеризацией их исследовательской деятельности (рис.1).
Более подробно остановимся на форме круглого стола в рамках конференций разного уровня для налаживания более тесных связей и пропаганды научно-исследовательской работы в молодежной среде.
Наш первый опыт в проведении круглого стола в рамках студенческой конференции органично нас подтолкнул на мысль о создании учебно-производственного кластера, о чем фактически пишет и Корчагина Н.А., а именно, что «университеты играют важную роль в качестве элемента кластеров, при этом имеет большой потенциал коллективных действий. Вузы являются структурными элементами кластеров, выполняют функцию научно-технического обеспечения бизнес-процессов, а также способствует реализации такого направления, как повышение использования знаний.
Таким образом, вхождение вуза в кластер формирует не спонтанную концентрацию разнообразных научных и технических изобретений, а определенную систему распределения новых знаний и технологий.
Вуз в этом случае выступает определенным фактором кластерной стратегии» [3, с. 51].
В современных экономических условиях требуется в конечном итоге коммерциализация деятельности, представляющей собой бизнес. И когда интересы, не противоречащие на взаимовыгодной и взаимопонимающей основе, достигнуты в рамках тематики круглого стола, то заключение договоров неизбежно в финале, по крайней мере, о дальнейшем сотрудничестве. Поэтому считаем, что смелее надо проводить подобные мероприятия с представителями указанной цепочки, заранее планируя цели и средства для их осуществления.
Подчеркнем еще одну особенность учебной деятельности студентов в системах дистанционного образования MOODLE и HECADEM, помимо пяти принципов, заложенных в них [2, c. 13], позволяющих при совместном их использовании, совершенствовании и системном подходе к их внедрению создать подобные кластеры по направлениям выбранной деятельности, например, в решении экологических проблем региона [1, с. 161]. Это возможно благодаря многовариантности представленной информации, инте-
34
рактивности обучения, создания постоянно активной справочной системы, самоконтроля действий, выстраивания индивидуальных образовательных траекторий, конфиденциальность и соответствие принципам успешного обучения, итогом которого может быть созданный кластер реальной деятельности со всеми функционирующими связями и экономическими расчетами.
В заключение отметим, что для создания кластеров в виде цепочки школа-вуз-производство-бизнес через фундаментальные и прикладные исследования необходимо использовать все появившиеся возможности, а именно, глобализацию процессов путем компьютеризации информационных и дистанционных технологий обучения. Конференции и круглые столы с привлечением представителей производства и бизнеса способствуют укреплению связей и созданию рабочих мест для творческой молодежи.
Первоочередную роль в этом процессе играет и система образования, которая нацелена на решение проблем, возникающих в производственной деятельности и в реализации готовой продукции в бизнес-структурах. Овладение финансовыми механизмами для расчета оптимальных вариантов сфер деятельности, а также их конкретной реализации, является важной составной частью современного образования.
Список литературы
1. Волкова С.Н., Сивак Е.Е., Потемкин С.Н. и др. Взаимодействие системы обучения и научно-хозяйственной деятельности в решении экологических проблем региона. Проблемы высшего образования: материалы международной научно-методической конференции. Хабаровск, 16-18 марта 2011г. // Изд-во Тихоокеанского государственного университета, 2011. С.13-15.
2. Денисова Т.Л. Особенности учебной деятельности студентов в системах дистанционного образования MOODLE и HECADEM: сравнительный анализ. Проблемы высшего образования: материалы международной научно-методической конференции. Хабаровск, 16-18 марта 2011г. // Изд-во Тихоокеанского государственного университета, 2011. С.161-163.
3. Корчагина Н.А. Основные факторы эффективной реализации кластерной политики. Вестник российского государственного
35
торгово-экономического университета. Научный журнал // Изд-во Москва, 2009. №10(37). С.48-53.
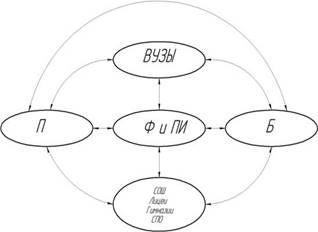
Рис.1. Учебно-производственный кластер на основе фундаментальных и прикладных исследований (Ф и ПИ); СОШ – средние образовательные школы; ВУЗы – высшие учебные заведения; П – производство; Б – бизнес.
S. N. Volkova, E. E. Sivak, M. I. Pashkova, N. A. Kostenko,V.V.Gerasimova e-mail:[email protected]
Kursk State Agricultural Academy named prof. I.I.Ivanov
THE UNIVERSITY AS THE FOCUS OF THE CLUSTER
STRATEGY STATE PERSONNEL TRAINING
The article refers to the creation of clusters on the basis of fundamental and applied research with the use of innovative technologies related to the modernization of education.
Key words: cluster, education, innovative technology, research, production, business, modeling.
36
УДК 51-8
М.Г. Гиоргадзе, Т.В. Меренкова, А.В. Ряднов e-mail: [email protected], Московский государственный университет путей сообщения (МИИТ)
РОЛЬ МАТЕМАТИЧЕСКОЙ ОЛИМПИАДЫ ПРИ
ПОДГОТОВКЕ КВАЛИФИЦИРОВАННЫХ КАДРОВ
В статье говорится о целесообразности, формах проведения математических олимпиад в вузах, в частности в Московском университете путей сообщения.
Ключевые слова: олимпиада, математика, студенты, преподаватели, задачи.
Олимпиады возникли в Древней Греции как состязания в ловкости, силе, красоте. Первая олимпиада состоялась в 776г. до н.э. Олимпиады проводились в Олимпии один раз в четыре года вплоть до 394 г.н.э., когда были запрещены в связи с распространением христианства. Вновь олимпиады возродились в 1896 году.
Различного рода состязания проводились не только в спорте. Хорошо известна любовь к состязаниям в решении задач как на Руси, так и во многих других странах мира. Математические соревнования по решению задач также называются олимпиадами, хотя они проводятся в настоящее время а периодом не в четыре года, а, как правило, ежегодно.
В России конкурсы по решению задач начали проводиться с 1886 г. Олимпиады имеют большое значение при решении ряда вопросов, относящихся к проблеме математического образования в нашей стране.
Одной из важных целей проведения математических олимпиад является развитие интереса студентов к математике. У многих студентов имеется большое желание проверить свои силы, математические способности, умение решать нестандартные задачи. Их привлекает возможность добровольного участия в соревновании, необычность всей обстановки на олимпиаде.
Для развития интереса студентов к математике имеет значение и спортивный азарт участников олимпиады. Дух соревнования за-
37
ложен во многих наших студентах, поэтому они желают посоревноваться со своими сокурсниками и в умении решать олимпиадные задачи.
Олимпиады способствуют выявлению и развитию математических способностей. Часто на занятиях студент не выделяется среди своих сокурсников и получает, вполне объективно, только тройки, а когда приходит на олимпиаду попробовать свои силы ему становится так интересно. И мы замечаем, что он неплохо решает задачи «на соображение», задачи с «изюминкой», при решении которых встают в тупик многие отличники. После олимпиады этот студент наверняка более серьезно займется предметом. А преподаватель поможет этому студенту, найдет пути развития способностей такого студента.
Любой участник олимпиады желает добиться лучших результатов. Для этого решает задачи, читает рекомендованную литературу, более подробно изучает отдельные вопросы математики. Он понимает, что для успеха на олимпиаде необходимо уметь по-разному решать задачи, развивать в себе способности анализировать решения задач и искать нешаблонные подходы к их решению, видеть неожиданные зависимости.
Победа студентов на каждом этапе приводит к повышению результативности его занятий математики.
Участвуя в математических соревнованиях, студент лучше, более объективно определяет свое отношение к математике как предмету будущей профессии. Есть немало случаев, когда студент в результате участия в математических олимпиадах начинает с увлечением заниматься математикой или каким-либо ее разделом, а затем выбирает математику или какой-либо вид математической деятельности в качестве своей профессии.
Проведение олимпиад по математике является прекрасным средством повышения деловой квалификации преподавателей.
Разбор материала для олимпиад, подготовка к проведению этого мероприятия является одной из форм активной работы преподавателя по повышению своей научно-методической квалификации. Подбор к олимпиаде нестандартных, требующих особых приемов решения задач предполагает наличие хороших навыков в этом деле от самих преподавателей.
38
Проведение олимпиад дают преподавателям эстетическое наслаждение. Здесь в свободной обстановке преподаватель занимается любимым предметом, да и аудитория здесь более активная и внимательная.
Преподаватель стимулирует участие в олимпиадах, победители олимпиад будут иметь преимущество при аттестации и сдаче экзаменов.
Различные олимпиады позволяют сравнить качество математической подготовки и математического развития студентов, а также состояние преподавания математики на различных курсах, специальностях.
Всероссийские олимпиады дают возможность в некоторой степени сравнивать состояние математического образования в отдельных областях, краях страны. Международные олимпиады позволяют сопоставить состояние верхней грани математического образования в вузах разных стран. Возможность такого сравнения весьма важна в век научно-технической революции, ибо позволяет странам, участвующим в олимпиадах, своевременно принять необходимые меры для устранения пробелов в содержании математического образования студентов, в осуществлении мероприятий по подготовке будущих специалистов.
В нашем университете ежегодно проводятся математические олимпиады для студентов всех курсов. Для успешного проведения олимпиад необходимо выполнение в первую очередь следующих условий:
1) систематическое проведение факультативных занятий по математике;
2) обеспечение регулярности проведения олимпиад;
3) cерьёзная, содержательная и интересная подготовительная работа перед проведением каждой олимпиады;
4) хорошая организация проведения олимпиад; 5) интересное математическое содержание соревнований.
Проведение всех олимпиад предполагает соответствующих студентов. Систематически должна проводиться индивидуальная работа с наиболее сильными или вообще интересующимися математикой студентами. Для проведения математических олимпиад создают оргкомитет и жюри. Они обеспечивают всю подготовительную работу, обеспечивают подбор заданий для проведения со-
39
ревнований, проверку работ участников, присуждают призы победителям.
При подборе заданий целесообразно придерживаться такого принципа, при котором из 8 задач, предлагаемых каждому участнику олимпиады, примерно 1-2 задачи должны быть посильны для большинства участников олимпиады. Такие задачи вселяют уверенность в силе большинства участников олимпиады, не отпугивают их от занятии математикой, хотя и не дают права на получение приза. 3-4 задачи дают повышенные трудности. Решивших хотя бы одну из таких задач получают возможность на получение определенного поощрения за успешное участие в олимпиаде. И 1-2 задачи сложные, как говорят, с изюминкой. Эти задачи требуют очень хорошей математической подготовки, особой математической смекалки и твердых навыков в решении нестандартных задач.
За 3-4 недели до проведения олимпиады оргомитет начинает план подготовительных мероприятий и порядок проведения олимпиады. За 2-3 недели вывешиваются объявления об олимпиаде, призывы к студентам подготовиться и принять участие в олимпиаде.
Подготовительные задачи, рекомендации по подготовке к олимпиаде задания, для проведения готовит оргкомитет и методическая комиссия.
Результаты олимпиады оформляются в виде решения оргомитета, результаты проводятся до сведении всех участников, преподавателей и студентов.
Победители институтской олимпиады направляются на университетскую олимпиаду.
Для принятия участия в всероссийской олимпиаде студенты проходят специальную подготовку на занятиях и после победы на всероссийской олимпиаде их награды вывешиваются на стенде нашего института и отмечаются приказом ректора.
M.G. Giorgadze, T.V. Merenkova, A.V. Rjadnov
Moscow State University of Railway Engineering (MIIT)
ROLE OF THE MATHEMATICAL OLYMPIC GAMES
BY PREPARATION OF QUALIFIED PERSONNEL
40
In article it is told about expediency, forms of carrying out the mathematical Olympic Games in higher education institutions, in particular at the Moscow university of means of communication.
Key words: Olympic Games, mathematics, students, teachers, tasks.
УДК 372.851 Л. А. Должикова
е-mail: [email protected]
Защитенская СОШ Щигровского района Курской области
ИСПОЛЬЗОВАНИЕ ИНФОРМАЦИОННЫХ
КОМПЬЮТЕРНЫХ ТЕХНОЛОГИЙ НА УРОКАХ
МАТЕМАТИКИ
Предложена методика преподавания математики в общеобразовательной школе с применением информационнокомпьютерных технологий, Цифровых образовательных ресурсов, сайтов для подготовке обучающихся к ОГЭ и ЕГЭ.
Ключевые слова: информационно-компьютерные технологии, презентация, эффективные методы обучения, активизация деятельности обучающихся.
В связи с тем, что происходит постоянное увеличение умственной нагрузки на уроках математики, каждый учитель начинает задумываться над тем, как поддержать интерес к изучаемому материалу у школьников, как увеличить их активность на протяжении всего урока. В связи с этим мною ведутся поиски новых эффективных методов обучения и таких методических приёмов, которые бы активизировали деятельность учащихся, стимулировали бы их получать знания, которые дает учитель, а также к самостоятельному приобретению знаний.
XXI век – век высоких информационных технологий. Каждый учитель может сказать, что в процессе информатизации образования возникает ряд проблем. Это недостаточный выбор программ,
41
несоответствие большинства имеющихся программных продуктов всем требованиям, необходимым для успешной организации учебного процесса, отсутствие или нехватка электронных информационных ресурсов.
Сейчас в образовательной практике всё более востребованным становится использование информационно-коммуникативных технологий, которые представляют собой ресурсы в локальных или глобальных сетях. Наиболее удобной формой для восприятия является материал, скомпонованный в единый обучающий комплекс.
Задачи, которые мы ставим на уроках с применением компьютерных технологий:
использовать на уроках различные формы работы с
применением ИКТ;
развивать творческие способности и познавательную активность учащихся при выполнении проектных и исследовательских работ;
воспитывать самостоятельность, способность к
самообразованию; использовать ИКТ как средство контроля и оценки качества
обучения;
сформировать информационную компетентность учащихся; научить учащихся применять знания работы с компьютером на других уроках.
Использование ИКТ позволяет проводить уроки на высоком эстетическом и эмоциональном уровне (музыка, анимация); обеспечивает наглядность; привлекает большое количество дидактического материала; повышает объём выполняемой работы на уроке; обеспечивает высокую степень дифференциации обучения (индивидуальный подход к ученику, применяя разноуровневые задания).
Программное обеспечение, которое мы используем на своих уроках весьма разнообразно. Это - программы-учебники; программы-тренажёры; словари, справочники; энциклопедии; видеоуроки; библиотека электронных наглядных пособий.
Эффективность использования мультимедийного проектора на уроке позволяет расширить возможности при изложении нового материала, достичь оптимального темпа работы ученика, повысить познавательный интерес. Использование этого же проектора при
42
проверке знаний учащихся позволяет нам проверить уровень знаний, выявить пробелы в знаниях, дисциплинирует учащихся, так как они понимают, что на таком уроке будут опрошены все и не удастся спрятаться за спины одноклассников.
Чаще всего в нашей работе мы используем мультимедийные презентации, которые сейчас можно найти в интернете, остается только доработать их под свой контингент учащихся. Сформировался запас презентаций, которые выполняют учащиеся самостоятельно дома. Это в основном презентации, которые содержат биографии ученых-математиков, занимательные страницы математики, исследовательские проекты, как индивидуальные, так и групповые.

В 2011 году мы прошли курсы по программе «Использование
ЭОР в процессе обучения в основной школе по математике». ЭОР (Электронные образовательные ресурсы) представляют собой открытые образовательные модульные мультимедиа системы. Портал Федерального центра информационно-образовательных
43
ресурсов (ФЦИОР) обеспечивают доступ к центральному хранилищу ЭОР системы образования, представляет собой единую современную технологическую платформу. В каталоге модули по 16 учебным предметам школьной программы с 5-го по 11–й класс.
В данном ресурсе можно найти много интересных разработок, которые можно применять при изучении нового материала, проверке знаний, контроле качества знаний.
Самое главное, что данный ресурс доступен даже детям с ограниченными возможностями.
44

Учащимся такие презентации помогают быстрее усвоить новый материал (с помощью схем и таблиц, в которых кратко и наглядно показан изучаемый материал), а ведь для слабоуспевающих учащихся каждый слайд – это опорный конспект, который ему легче запомнить, а потом воспроизвести. Из этого можно сделать вывод, что компьютер формирует навыки рационального запоминания материала. При объяснении нового материала каждый слайд мы комментируем, по необходимости сопровождаю дополнительными объяснениями и примерами. Урок от этого становится интереснее. По итогам таких уроков можно значительно повысить эффективность обучения.
Результатом применения информационно-коммуникативных технологий на уроках является повышение квалификации учителя, вовлечение большего количества учащихся в активную деятельность, активизирует внимание учащихся, усиливают их мотивацию, возрастает интерес учеников к предмету, развивает воображение и фантазию, а с этим и повышается эффективность урока. Все это служит залогом глубоких и прочных знаний по предмету и предопределяет развитие личности учащегося.
45
Сейчас очень много различных сайтов для подготовки к ОГЭ и ЕГЭ. Одним из которых мы пользуемся наиболее часто – это «Сдам ГИА» и «Решу ЕГЭ». На этих сайтах в режиме «On-line» можно проверить, как учащиеся готовятся к экзаменам.

Конечно, не стоит забывать о здоровьесберегающих факторах. Для каждого класса есть временные нормативы, которые необходимо соблюдать при использовании ИКТ на уроках.
В заключении обобщим вышесказанное. Применение информационно-компьютерных технологий представляет уникальную возможность для творчества учителя, для развития самостоятельной и исследовательской деятельности обучающихся, развиваются активно-деятельностные формы обучения, которые способствуют осознанию обучающимися процесса обучения, развивают познавательную активность, помогают достижению наивысшего возможного результата в общем развитии всех учеников, в том числе самых сильных и самых слабых, позволяет провести рефлексию знаний.
ССЫЛКИ
1. http://school-collection.edu.ru/
2. http://fcior.edu.ru
3. http://сдамгиа.рф/?redir=
4. http://reshuege.ru:82
5. http://www.edu.ru/db/portal/sites/res_page.htm
L. A. Dolzhikova e-mail: [email protected]
Zashchtenskaya school Shchigrovsky district, Kursk region
THE USE OF INFORMATION COMPUTER TECHNOLOGY
IN MATHEMATICS LESSONS
Methods of teaching mathematics in the secondary school with the use
46
of information and computer technology, Digital educational resources, sites for the training of students to the DGE and the exam.
Key words: information and computer technology, presentation, effective learning activities of students.
УДК 378.51
Г.А. Есенкова1, Е.С. Есенкова2 e-mail: [email protected]1, [email protected]2
1
Юго-Западный государственный университет, Курск
2
Средняя общеобразовательная школа №19, Курск
ПОВЫШЕНИЕ КАЧЕСТВА ПРОВЕРКИ ЗНАНИЙ
ПО РАЗЛИЧНЫМ РАЗДЕЛАМ МАТЕМАТИКИ
НА ОСНОВЕ ФОРМИРОВАНИЯ СИНХРОННЫХ
БЛАНКОВ ТЕСТОВ И ОТВЕТОВ
В статье представлена оригинальная форма тестирования с помощью разработанных авторами синхронных бланков заданий и ответов, позволяющая выяснить степень знаний тестируемого по конкретному вопросу.
Ключевые слова: образовательные стандарты, тестирирование, контрольный опрос, математика, студенты, обучающиеся, задачи, вопросы.
В настоящее время возрастает потребность в математизации инженерных, экономических и многих других дисциплин, что очень приятно математикам. При этом нельзя не отметить, что, сокращается время на изучение программ, отсутсвует эффективный контроль знаний, умений. В связи с этим, важный аспект организации учебных занятий – оптимиация контроля знаний и умений. Проверка знаний студентов в учебном процессе является одной из наиболее серьезных проблем методики преподавания в вузе.
Важно помнить о необходимостью достижения студентами определенного уровня знаний и при этом заботиться о возможности учитывать их индивидуальныеособенности.
|
47 В последние годы повышенное внимание уделяется тестиро- |
48 Таблица 1 |
 ванию студентов и школьников,
причем в самых разнообразных формах. Проведение тестов на практических или на дополнительных
занятиях дает возможность преподавателю осуществлять постоянный контроль, помогает
составить представление об усвоении студентами тех или иных тем и отчасти позволяет
в определенной мере оценить индивидуально каждого студента
ванию студентов и школьников,
причем в самых разнообразных формах. Проведение тестов на практических или на дополнительных
занятиях дает возможность преподавателю осуществлять постоянный контроль, помогает
составить представление об усвоении студентами тех или иных тем и отчасти позволяет
в определенной мере оценить индивидуально каждого студента
Несколько лет тому назад авторы статьи поставили перед собой цель – разработать специальные бланки заданий тестов и бланки ответов тестов, которые способствовали бы качественной и бытрой проверке работ студентов с учетом индивидуального подхода.
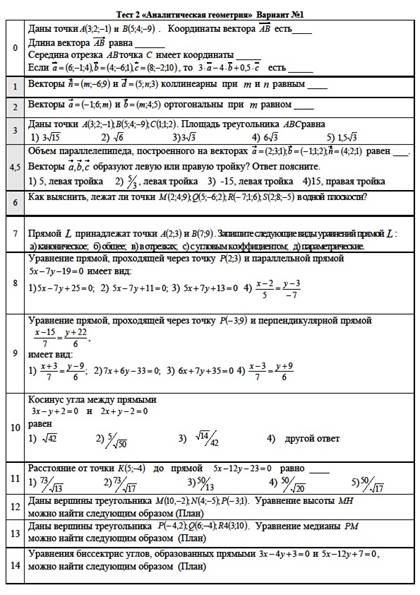
Начался эксперимент с создания теста по аналитической геометрии. Задания теста были размещены на одном листе формата А4, две страницы на листе. Бланк ответов также помещается на лист формата А-4. Бланк заданий и бланк ответов приведены в таблицах 1 и 2
Апробация таких бланков заданий и бланков ответов показала, что студенты успешно выполняли тесты, по собственному желанию приходили переписывать работы для получения лучших в личном зачете результатов. Им была наглядно представлена картина их знаний и практических навыков по изученному материалу. Как видно из содержания бланка, для зачтения работы достаточно набрать 84 балла, а всего можно набрать до 122 баллов. Это не в последнюю очередь подталкивает студентов на выполнение заданий на баллы, превышающие 100 баллов.
Оформление и удобство выбора заданий и заполнения бланков выступают, как дополнительный благоприятный фактор при выполнении студентами заданий работы. Есть маневр для выбора, прослеживается возможность проверить свои силы, показать свои способности другим.
49 50
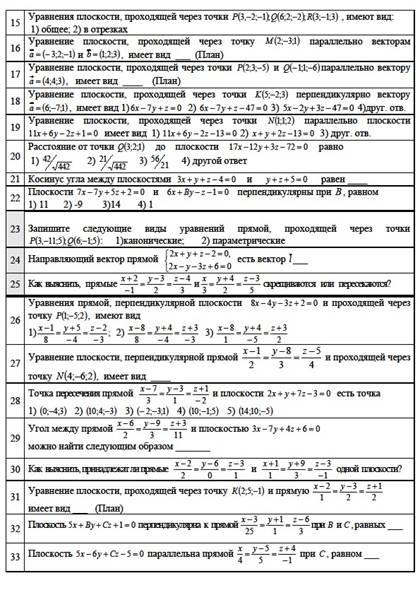
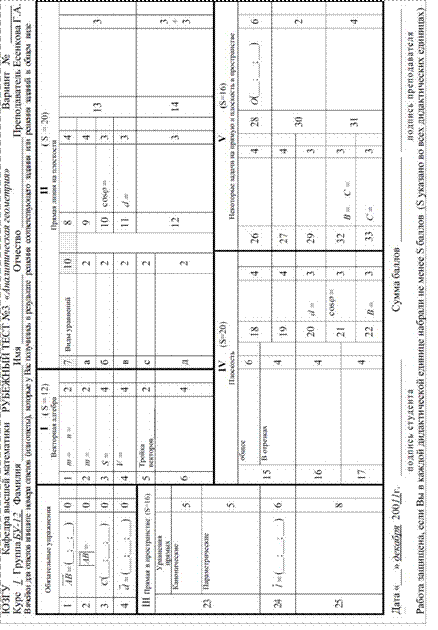 Таблица 2
Таблица 2
|
51 Отстающие студенты, о которых также следует думать, воз- |
52 Таблица 3 |
 можно, даже в большей
степени, выигрывают. При небольшом багаже знаний можно найти вопросы, на которые
они смогут дать ответы. С другой стороны, тон задают задания уровня 0. Зайти в тест,
можно только, преодолев своего рода барьер. Необходимо всего лишь вспомнить простейшие
вопросы, известные из школьного курса оп теме «Векторы в пространстве».
можно, даже в большей
степени, выигрывают. При небольшом багаже знаний можно найти вопросы, на которые
они смогут дать ответы. С другой стороны, тон задают задания уровня 0. Зайти в тест,
можно только, преодолев своего рода барьер. Необходимо всего лишь вспомнить простейшие
вопросы, известные из школьного курса оп теме «Векторы в пространстве».
Дальнейшее применение бланков вопросов и ответов по теме «Аналитическая геометрия» также имело успех и популярность у студентов.
В связи с этим возникла идея создания подобных пар бланков по другим темам математики, но уже с модификацией. Что, если бланки вопросов и ответов будет и внешне выглядеть одинаково? Назовем их условно «синхронными». В дальнейшем, можно к каждому варианту заданий на бланках ответов готовить ответы, возможно, с некоторыми указаниями и подсказками. Это ускорит процесс проверки работ,
Причем сделает ее возможной даже в присутствии студента. В бланки для ответов следует помещать ответы, полученные с помощью каких-нибудь программ, позволяющей это сделать. Например, с помощью системы MathCad различных версий или же онлайнсервиса WolframAlfa. Тогда у студентов будет уверенность в предложенных им ответах и желание самим научиться получать ответы или решения с помощью программ.
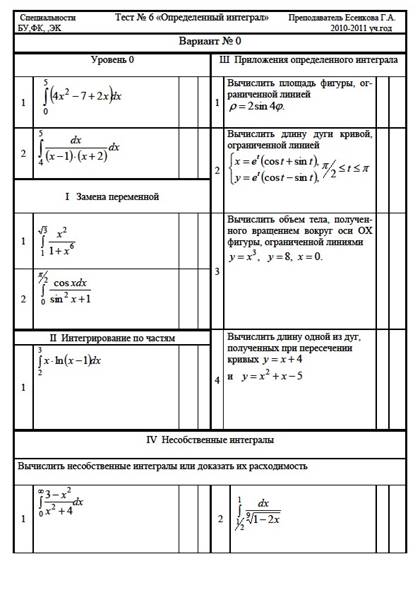
В статье предлагаем вариант простейшего по устройству теста «Определенный интеграл» и «синхронного бланка» к нему. (Табл.3 и Табл.4). Оставлены пустыми ячейки с количеством баллов, так как баллы можно вписывать после обсужения со студентами после выполнения ими теста.
Здесь видны преимущества подобных бланков перед «неорганизованными» вариантами своих аналогов. Понятно, куда записывать ответы, возможно указать только формулы. И, если студент не может выполнить практическое задание, то, возможно, справится с теоретическим простейшим вопросом, который подразумевает краткий и четкий ответ. Если студенту не удается выполнить прак-
тическое задание целиком, то у него есть возможность выписать замену, которая может использоваться в данной задаче.
|
53 Таблица 4 |
54 Такие варианты успокаивают студента, дают ему возможность |
 сосредоточиться на выполнении
заданий, а не на страхе перед результатом.
сосредоточиться на выполнении
заданий, а не на страхе перед результатом.
В опытно-экспериментальной стадии бланки корректровались при активном участии студентов 1-2 курсов экономического и строительного факультетов ЮЗГУ. Уточнялось количество баллов по тем или иным заданиям, распределялись баллы по всему тесту и по разделам. Сами задания подвергались достаточно суровой критике. Следует отметить, что наиболее заинтересованными были студенты, которые планировали после окончания вуза поступать в аспирантуру с дельнейшей целью стать преподавателеми.
С интересом восприняли «синхронные» бланки ученики 10-х классов школы №19 г. Курска при изучении тем «Тригонометрические функции», «Тригонометрические уравнения» и «Преобразования тригонометрических выражений». Было разработано несколько бланков с количеством заданий, достаочно хорошо отражающим картину освоения тригонометрии в целом.
Представленная технология создания бланков заданий и бланков ответов отличается ориентированностью на индивидуальный подход к каждому студенту. Наравне с подчеркнутой особенностью следует отметить, что предложенная технология контроля является легкодоступной и не вызывает затруднений в использовании в учебном процессе.
G.A. Esenkova1, E.S. Esenkova2 e-mail: [email protected] 1, [email protected] 2
1
Southwest State University, Kursk,
2
Secondari scool №19, Kursk
EXAMINATION IMPROVEMENT QUALITY
ACCORDING TO VARIOUS SECTIONS OF MATHEMATICS
BASED ON SYNCHRONIZATION OF TESTS AND ANSWERS
The article presents developed by the authors the original test form based on tasks and responses, allowing to determine knowledge degree
of a particular subject.
55
Key words: educational standards, test, quiz, mathematics, students, the trained, tasks, questions
УДК 378:51
Д.А. Жураев, Ж.Н. Жумаев e-mail: juraev_[email protected]
Каршинский Государственный Университет, (Узбекистан)
ПРИМЕНЕНИЕ ПРОГРАММЫ MAPLE В УРОКАХ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
В работе приведено вычислений некоторых дифференциальных уравнений, используя системы Maple.
Ключевые слова: линейные уравнения, уравнения Бернулли.
В работе описаны некоторые приемы решения обыкновенных дифференциальных уравнений в пакете компьютерной математики Maple. Приведены задания для самостоятельного решения.
Определение 1. Дифференциальное уравнение называется линейным относительно неизвестной функции и ее производной, если оно может быть записано в виде: y P(x)y Q(x),
при этом, если правая часть Q(x) равна нулю, то такое уравнение называется линейным однородным дифференциальным уравнением, если правая часть Q(x) не равна нулю, то такое уравнение называется линейным неоднородным дифференциальным уравнением.
P(x) и Q(x)- функции непрерывные на некотором промежутке a<x<b. Общее решение данного уравнения можно искать в следующем виде
y eP(x)dx Q(x)eP(x)dxdx C
2 , (1)
Определение 2. Уравнением Бернулли называется уравнение вида
y Py Q yn,
56
где P и Q – функции от х или постоянные числа, а n – посто-
янное число, не равное 1.
Для решения уравнения Бернулли применяют подстанов-
1
ку z ![]() ,
с помощью которой, уравнение Бернулли приводится к
,
с помощью которой, уравнение Бернулли приводится к
n1
y
линейному.
Решение этого уравнения будем искать в виде:
z eP1dxQ1eP1dxdx C, (2)
Q1 (n1)Q; P1 (n1)P.
1
![]()
Пример 1. Решить уравнение x2 y y ax2ex.
Сначала приведем данное уравнение к стандартному виду:
1
![]()
y ![]() 1 y
aex.
1 y
aex.
2
x
1
![]()
Применяя формулу (1), получим:
P
![]() 1 ; Q
aex; x2
1 ; Q
aex; x2
![]() dx
dx ![]() 1 1
1 1
y e x12 aexe x2dxdx C,
![]() 1 1 1
1 1 1 ![]() 1
1
y exaexe xdx C exadx C,
1
![]()
y ex (ax C).
Решим теперь это уравнение в пакете Maple. Запишем уравне-
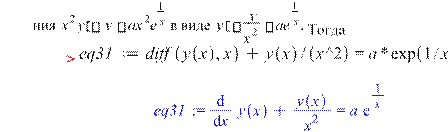
57
Определяем тип дифференциального уравнения с помощью функции odeadvisor подпакета DEtools
![]()
Тип [_linear] отвечает линейным уравнениям. Решаем уравнение с помощью функции dsolve
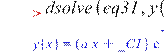
Пример 2. Решить уравнение xy y xy2 ln x.
![]() Разделим уравнение
на xy2: y
1
1
ln x.
Разделим уравнение
на xy2: y
1
1
ln x.
y2 x y
1 y
Полагаем z ![]() ; z
; z
![]() . y y2
. y y2
1 1
z ![]() z ln
x; z
z ln
x; z ![]() z ln
x. x x
z ln
x. x x
1
Здесь P ![]() , Q ln x.
, Q ln x.
x
![]()
![]() dx
dx
z e dxx ln xe x dx C; z elnx ln xelnxdx C;
![]() dx
dx
z x ln x x C; z x ln xd(ln x) C ;
ln2
x
z
x ![]() 2 C
2 C
Произведя обратную подстановку, получаем:
1 ln2 x
![]()
![]()
x
x
y 2 C.
Решим теперь это уравнение в пакете Maple. Уравнение
xy
y
xy2 ln x
запишем в виде y
![]() y
y2 ln x. Тогда
y
y2 ln x. Тогда
x
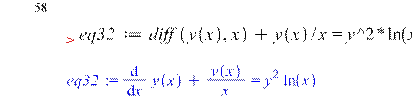
.
Определяем тип дифференциального уравнения с помощью функции odeadvisor подпакета DEtools
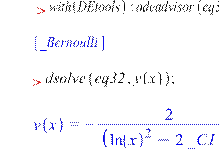
Пример 3. Решить задачу Коши для уравнения Бернулли
![]() x y y e y y
2 ; (0)
x y y e y y
2 ; (0)
![]() .
.
Используя пакет Maple, имеем
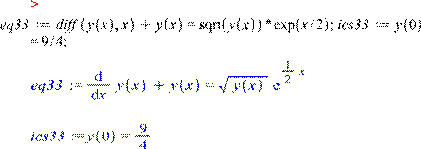
Решаем уравнение с начальными условиями
> ![]()
59
![]()
Строим поле направлений и выделяем искомую интегральную кривую
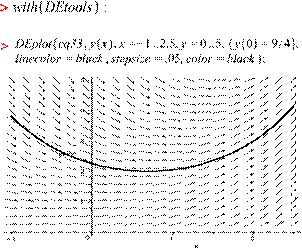
2
ех х
Ответ:.
y
![]() 2 1
е
2 1
е
Задачи для самостоятельного решения.
1.
xy
4y
x2![]()
2. xy 2y 2х4;
3. 2х 1у 4х 2у;
4. y ytgx secx;
5. хe exdx xdy 0;
6. x2 y xy 1 0;
7. y 2y y2ex;
8. y y4 cosx ytgx;
9. xy2y x2 y3;
10. xydy y2 xdx;
60
11.
![]() xy 2x2 y
4y;
xy 2x2 y
4y;
12. yx3 sin y xy 2y.
Список литературы
1. Савотченко С.Е., Кузьмичева Т.Г. С13 Методы решения математических задач в Maple: Учебное пособие. Белгород: Изд. Белаудит, 2001.116 с.
2. Филиппов А.Ф. Сборник задач по дифференциальным уравнениям. М.: Наука, 1979. 128 с.
3. Черненко В.Д. Высшая математика в примерах и задачах: Учебное пособие для студентов втузов. В 3-х ч. Т. I. СанктПетербург.: Политехника, 2003. 703 с.
D.A. Juraev, J.N. Jumaev e-mail: juraev_[email protected]
Karshi State University,(Uzbekistan)
APPLICATION OF PROGRAM MAPLE IN LESSONS OF THE
DIFFERENTIAL EQUATIONS
The paper presents calculations of certain differential equations
using the system Maple
Key words: linear equations, Bernoulli equation.
61
УДК 51
С.А. Жураева1, Н.Ш. Нурматова2 e-mail: [email protected], [email protected]
1
Средняя школа № 61, Шахрисабзкий район, (Узбекистан)
2
Каршинский медицинский колледж, Г. Карши, (Узбекистан)
ЦЕЛАЯ И ДРОБНАЯ ЧАСТЬ ЧИСЛА
В работе рассмотрено метод решений уравнений с целой и дробной части.
Ключевые слова: целая часть, дробная часть.
В работе рассмотрено решение уравнений с целой и дробной части и их метод решений. Приведены задания для самостоятельного решения.
Начнем с определений.
Целой частью действительного числа x называется наибольшее целое число, не превосходящее x.
Целая часть числа x обозначается через x.
Например,
5,8 5, 5,86
Из этого определения следует важное неравенство:
x x x1, (1)
Дробной частью действительного числа x называется разность между x и целой частью x.
Дробная часть числа x обозначается через x. Тогда
x x x , (2)
Например,
5,8 5,8 5 0,8; 5,85,8 ( 6) 6 5,8 0,2
Из равенства (2) следует, что
xxx, (3)
Например,
5,8 ( 6) 0,2
Целая часть числа х принимает только целые значения: xZ.
Что касается дробной части, то она удовлетворяет неравенству
62
0 x1, (4)
Для доказательства неравенства (4) отнимем от всех частей неравенства (1) число x.
xxxxx 1 x, 0 x1 Перейдем к задачам.
Пример 1. Решить уравнение x1x 215
На основании равенства (3)
x1x1, x 2x 2. Теперь получаем:
x1 x 2 15, 2x 1 15, 2x14, x 7.
При каких x целая часть x равна 5? При всех, удовлетворяющих неравенству 5 x 6.
Ответ: 5 x 6. #
Пример 2. Докажите неравенство:
m n mn.
Сложим почленно неравенства:
m m m 1,
n n n 1.
Будем иметь:
mn m n m n 2.
Тогда чему же равна целая часть суммы m n ? Или mn, или
mn1.
В обоих случаях
m n mn. #
Пример 3. Решите уравнению:
![]() x2x
3x x4
ggg 2000x .
x2x
3x x4
ggg 2000x .
Из условия следует, что число xцелое. Воспользуемся неравенством:
x x x x x x x x x
![]()
![]()
2
3
6
2 3 6 x
2
3
6 3.
2
3
6
2 3 6 x
2
3
6 3.
Может возникнуть вопрос: почему именно этим неравенством? Уже потому, что
x x x
![]()
x.
x.
2 3 6
Отсюда
63
x x x x x x
![]()
![]()
2
3
6
3 x
2
3
6 .
2
3
6
3 x
2
3
6 .
Прибавим ко всем частям последнего неравенства x, т.е. сумму, стоящую в правой части исходного уравнения:
x x x x x x x x
![]()
![]()
4
5
7
ggg 2000
3 0
4 5 7
ggg 2000.
4
5
7
ggg 2000
3 0
4 5 7
ggg 2000.
Тогда
x x x x
![]() 0
4
5
7
ggg 2000
3.
0
4
5
7
ggg 2000
3.
Следовательно, x 0 . Кроме того, все слагаемые суммы
из последнего неравенства, начиная с третьего слагаемого, равного ![]() 7x,
7x,
равны нулю. Отсюда x 7.
Осталось перебрать случаи:
x 0,1,2,3,4,5,6.
Подходят только 0, 4 и 5. Ответ: 0,4,5 . #
Задачи для самостоятельного решения.
1. ![]() x23
x 3 2;
x23
x 3 2;
2. x x 83 7x82;
3. xx 2x 418;
4. 2x 1 2x 3 2x1;
5. ![]() x 1x
x
1x ;
x 1x
x
1x ;
6. x 1 x 2 2;
7. sin x cosx 54x;
8. x ![]() x ;
x ;
9. 2x 1 x 1;
10. x 1 x;
11. ![]() 6x85
15x57;
6x85
15x57;
12. x 1x 2x 3gggx 100 200x;
13. xx 1;
14. x x 1 1;
64
15. cosx x2 1;
16. tgx 2cos2 x;
17. sin x cosx 1;
18. sin xsin x sin ;x
14. x2 x 2;
15. xx3 3;
16. x x 1;
Список литературы
1. Галкин Е.В. Нестандартные задачи по математике. Алгебра: Учеб. пособие для учащихся 7-11 кл. Челябинск: «Взгляд», 2004.
448 с.
2. Баранова И.В., Борчугова 3.Г. Сборник задач по элементарной алгебре: Учебное пособие для студентов педагогических институтов. Изд. 3-е. М.: Просвещение, 1987. 368 с.
3. Баранова И.В., Ляпин С.Е. Задачи на доказательство по алгебре: Пособие для учителя. Л.: Учпедгиз, 1954. 160 с.
4. Бартенев Ф. А. Нестандартные задачи по алгебре: Пособие для учителей. М.: Просвещение, 1976. 95 с.
5. Алгебра: Учебник для 9 класса средней школы / Под ред. С. А. Теляковского. 2-е изд. М.: Просвещение, 1993. 272 с. (Раздел
«Задачи повышенной трудности».)
6. Алгебра и начала анализа: Учебник для 10-11 классов средней школы / Под ред. А. Н. Колмогорова. 6-е изд. М.: Просвещение, 1997. 320 с.
7. Алгебра и начала анализа: Учебник для 10-11 классов средней школы. / Ш.А. Алимов, Ю.М. Колягин, Ю.В. Сидоров и др. 3-е изд. М.: Просвещение, 1994. 254 с. (Раздел «Задачи для внекласс-
ной работы».)
S.A. Juraeva1, N.Sh. Nurmatova2 e-mail: [email protected], [email protected] 1High school № 61, district Shakhrisabz, (Uzbekistan)
2
Karshi medical college, Karshi city, (Uzbekistan)
WHOLE AND THE NUMBER FRACTIONAL PART
65
In work it is considered a method of solutions of the equations with whole and a fractional part.
Key words: an integer part, a fractional part.
УДК 519.677
Н.К. Зарубина e-mail: [email protected]
Юго-западный государственный университет, Курск
ОНЛАЙН-СЕРВИС WOLFRAM ALPHA В
ОБРАЗОВАТЕЛЬНОМ ПРОЦЕССЕ
В статье рассмотрены основные возможности использование онлайн-сервиса WolframAlpha в образовательном процессе для повышения качества прикладной математической подготовки студентов.
Ключевые слова: wolfram alpha, математическая подготовка
«Мне бы хотелось увидеть обновленную, измененную программу обучения математике, от начала до конца построенную на компьютерных технологиях. Я даже не думаю, что мы должны называть этот предмет математикой. Но я уверен, что это один из главных предметов будущего»
Конрад Вольфрам, директор по стратегическому и международному развитию WolframResearch
В связи с увеличением информатизации (и, как следствие, математизации) общества возросли требования к информационной и математической подготовке выпускников. Студент должен уметь не только использовать математический аппарат в своих расчетах и исследованиях, но и анализировать полученные данные.
К сожалению, аудиторная нагрузка не позволяет уделить должное время прикладным аспектам. Поэтому на помощь приходят различные пакеты прикладных программ, один из которых – онлайн-сервис WolframAlpha, в основе работы которого лежит система компьютерной алгебры Wolfram Mathematica.
66
Прежде чем мы перейдем к обзору областей применения WolframAlpha в образовательном процессе, нельзя не отметить 2 преимущества сервиса:
1. Простота в использовании. Язык запросов сервиса интуитивно понятен, и в нем нет таких строгих правил синтаксиса, как в других прикладных программах;
2. Доступность. В отличие от других пакетов прикладных программ, онлайн-сервисом можно пользоваться в любом браузере с выходом в Интернет (включая мобильные устройства, на которые можно установить приложение сервиса).
Итак, давайте посмотрим, как можно использовать сервис WolframAlpha в образовательном процессе.
1. Вычисления и математические операции
Это основная задача сервиса. И, в зависимости от поставленной задачи, вы можете получить ответ или же проверить свое решение.
Более того, в платной PRO-версии сервис позволяет для некоторых задач (вычисление пределов, производных, интегралов и других) посмотреть пошаговое решение.
2. Визуализация результатов
WolframAlpha практически ко всем запросам выдает визуализацию данных. Это позволяет студентам лучше понять, над какими задачами они работают.
Так, допустим, при изучении тем в интегральном исчислении «Вычисление дуги кривой» или «Нахождение площади криволинейной трапеции» (рис.1, рис.2) сервис всегда выводит и искомую дугу кривой, и площадь криволинейной трапеции. Это позволяет студентам не только лучше понять, что они считают, но и научиться анализировать эмпирические данные.
3. Экспресс-анализ экспериментальных данных
Сервис позволяет провести экспресс-анализ данных. К примеру, если в WolframAlpha ввести запрос, состоящий только из числовых значений эмпирических данных, сервис выдаст не только числовые характеристики вариационного ряда (для ручного подсчета которых понадобилось бы значительное количество времени), но и полигон с гистограммой частот.
67
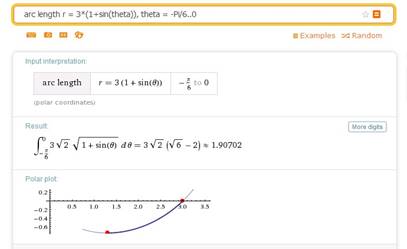
Рисунок 1 – Пример вычисления дуги кривой в полярной системе координат в онлайн-сервисе WolframAlpha
4. Привлечение студентов к научно-исследовательской работе
Несмотря на кажущуюся простоту запросов, возможности сервиса не ограничиваются лишь вычислением производных, пределов и интегралов – они гораздо шире. И, поскольку русскоязычной литературы по использованию WolframAlpha нет, студенты активно участвуют в освоении сервиса, открывая для себя новые его грани и представляя полученные результаты на конференциях.
Конечно, сервис WolframAlpha не лишен недостатков. Так, изза своей мобильности в нем нельзя использовать последовательность запросов, задавать процедуры или функции и т.д. Также нерадивые студенты могут использовать сервис не для восполнения «недостающих» знаний, а просто для списывания.
Однако возможности сервиса «перекрывают» его недостатки, поскольку все же главная его цель использования в образовательном процессе – это мобильность и экспресс-анализ данных (возможность быстро получить результат, сверить свой ответ, найти ошибку в ходе своих вычислений, визуализировать полученные данные, проанализировать полученный результат и т.д.).
68
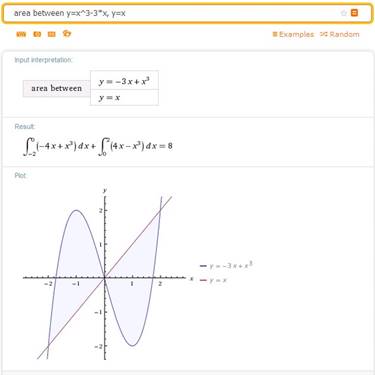
Рисунок 2 – Пример нахождения площади криволинейной трапеции в онлайн-сервисе WolframAlpha
Поэтому целесообразное, методически оправданное использование онлайн-сервиса WolframAlpha (и на аудиторных занятиях, и при самостоятельной исследовательской работе) позволяет эффективнее развить профессиональные компетентности студентов в соответствии с требованиями ФГОС.
_____________________________________
1. Д.А.Власов, А.В. Синчуков. Новые технологии WolframAlpha при изучении количественных методов студентами бакалавриата // Вестник РУДН (серия «Информатизация образования»). 2013. №4.
N.K. Zarubina e-mail: [email protected] South-West State University
69
ONLINE-SERVICE WOLFRAM ALPHA IN EDUCATION
In this article are shown main capabilities of online-service Wolfram Alpha in education for improving quality of students’ mathematical preparation.
Key words: wolfram alpha, mathematical preparation.
УДК 517.3 Л.С. Крыжевич e-mail: [email protected]
ФГБОУ ВПО «Курский государственный университет», Курск
ВЫЧИСЛЕНИЕ ПЛОЩАДИ ПОВЕРХНОСТИ ОБЛАКА
ТОЧЕК, ПОЛУЧЕННЫХ СКАНИРОВАНИЕМ
ИССЛЕДУЕМОГО ТЕЛА
В работе рассматриваются математические аспекты численного вычисления поверхности тела, заданного облаком отдельных точек, после сканирования и создания его трехмерной модели.
Ключевые слова: площадь поверхности, 3D-моделирование
Введение. Сегодня, практически, любая проблема, связанная со здоровьем, поддаётся коррекции. Так, в случае нарушения в работе любого органа, происходит его воспаление, вследствие чего он увеличивается в объеме. Но в случае увеличения, например, в 1,5 раза, на площадь поверхности органа на снимке увеличивается на 31%. Поэтому прямые измерения размеров тела весьма косвенным образом описывают изменения, происходящие с органом. В настоящее время в помощь врачам разрабатывается и внедряется множество новых методов лучевых исследований, но, несмотря на это, использование наиболее популярных методов поперечных сечений позволяет только вычислять объемы тел. Современное сложное и дорогостоящее томографическое оборудование использует в своей основе сечения тел и неприменим, когда тело задано с помощью проекций,
70
следовательно, не позволяет по данным вычислить площадь поверхности этого тела.
Поэтому существует острая необходимость в разработке способа измерения объема и площади поверхности тела всего по двум его проекциям и углу между ними. Он позволит по минимальному количеству данных определить объем тела и не требует сложного и дорогостоящего оборудования. Изучению данных вопросов и посвящено данное исследование.
Цель этапа исследования: является разработка методов обработки медицинских снимков, с целью вычисления площади поверхности изображенных на них органов.
Задачи этапа исследования:
1)Создание метода и алгоритма оптимизации изображения и анализа данных на снимке.
2)Разработка и отладка алгоритма синхронизации нескольких снимков.
3)Разработка технологии интерполирования поверхности по растровому изображению проекции и вычисления её площади.
Разработка относится к численным методам прикладной математики и может быть использовано для цифровой обработки медицинской графической информации и вычисления объемов и площадей поверхности нелинейных тел и внутренних органов.
Теоретическая часть. В процессе медицинского обследовании проводят съемку анализируемого тела с двух ракурсов (фотография, рентген-снимок или снимок УЗИ) и измеряют угол между осями съемки. В дальнейшем производятся замеры длины y, шириныx и высоты z снимков данного тела по максимальному значению. В полученных изображениях выделяются пограничные точки и данные оптимизируются для увеличения контрастности границ между объектами. В оптимизированных снимках врач отмечает пограничную область органа и алгоритм автоматически выделяет этот орган на обеих снимках. Заданные области автоматически обрезаются и синхронизируются по ширине, а также «разрезаются» на максимально возможное количество полос n одинаковой ширины
Δx.
Затем выбираются представители y(x) и z(x) из каждой полосы. Вычисления над оцифрованными снимками проекций производятся
71
при помощью ЭВМ, то есть вычисляют более точное среднее значение yi и zi, путем вычисления площади i-ой полосы и деления её на ширину полосы Δx, т.е.:
xi1 xi1
y(x)dx z(x)dx
xi xi
yi
![]() ; zi
; zi ![]() ; xi1xi xi1xi
; xi1xi xi1xi
На следующем этапе строят i-ый слой для данного тела по данным Δx, yi и zi.
Найденные на предыдущем этапе значения y(x) и z(x) играют роль параметрических размеров фигуры, положенную в основу модели. В связи с чем длину криволинейной дуги слоя можно записать в виде неявно заданной функции:
Pc(x,) f y(x),z(x),;
а, в силу того, что обе проекции разрезались на полосы одинаковой ширины Δx, площадь i-ого слоя поверхности вычисляют по формуле:
S p(x,) Pc(x,)dx;
где Sp(x,) – площадь поверхности i-ого слоя, полученного из частей проекций,
Pc (x,) – периметр i-ого слоя, полученного из проекций, dx– линейная часть ширины каждой полосы в проекциях, – угол между 1 и 2-ой проекциями.
Далее интерполируется площадь поверхности исследуемого тела. По заданному алгоритму полученные поверхности интегрируются и вычисляются площадь поверхности объекта и площади его проекций.
Площадь
поверхности возможной области вычисляют, проинтегрировав значения площадей i-ых
слоев: ![]() n
n
S p () lim S p (x,) Pc(x,)dx;
x0 i1
72
Если в основе полученная области будет положена форма параллелограмма, то мы получим точное верхнее значение искомой площади.
Найденные ранее усредненные значения y(x) и z(x) играют роль высот в этом параллелограмме, поэтому периметр слоя возможно вычислить по формуле:
![]() Pic 2
yi
zi ,
Pic 2
yi
zi ,
sin sin
Т.к. обе проекции разрезались на полосы одинаковой ширины Δx, площадь i-ого слоя поверхности вычисляют по формуле:
![]() Sip(x) Pic(x)x 2
y(x)
z(x) x
Sip(x) Pic(x)x 2
y(x)
z(x) x
sin sin
![]()
![]() 2x y(x) z(x)
2Siy
Siz , sin sin
2x y(x) z(x)
2Siy
Siz , sin sin
где Sip – площадь поверхности i-ого слоя, полученного из частей проекций,
Siy yi x, Siz zi x – площади i-ой полосы первой и второй проекции соответственно,
Pic – периметр i-ого слоя, полученного из проекций, yi – длина i-ой полосы в первой проекции, zi – ширина i-ой полосы во второй проекции,
x– ширина каждой полосы в проекциях, – угол между 1 и 2-ой проекциями.
Эта операция повторяется для всех n полос. Верхняя грань площади поверхности возможной области, которая ограничивает размеры исходного тела вычисляют, проинтегрировав значения площадей i-ых слоев:
73
![]() S p lim n Sip
lim n Picx lim n 2yi zi x
S p lim n Sip
lim n Picx lim n 2yi zi x
x0 i1 x0 i1 x0 i1 sin
2 n y z 2S y S z
![]() lim S S
lim S S ![]() ; sinx0 i1 i i sin
; sinx0 i1 i i sin
Все вышеуказанные равенства являются эквивалентными, поэтому возможно вычисления площади полной поверхности по любой из них.

Рисунок 1 - Послойная интерполяция поверхности тела
При использовании численных методов математики, n следует
увеличивать до тех пор, пока не будет достигнута необходимая точность вычислений ε, т.е. ![]() Sn1 Sn2
Sn1 Sn2 ![]() ,
где n2>n1.
,
где n2>n1.
Точность вычислений увеличивается, при увеличении числа n. Излишние итерации отсекаются, если были достигнуты результаты с требуемой точностью ε.
Результаты вычислений способом бесконтактного измерения площадей поверхностей подтверждаются контрольными физическими измерениями и использованием эталонов.
Апробация результатов. Эксперимент проводился на рентген-снимках печени добровольца: было сделано 2 снимка – фронтальный и под углом 75 градусов. В оцифрованных снимках были выделены границы органа, а также на обеих проекциях внутренняя часть выделенной области была залита черным цветом,
74
наружная – белым. Излишние белые поля были обрезаны вокруг рамки проекции органа. На следующем этапе были измерены размеры снимков, которые получились 22,4 см в длину, 15 см в ширину и 8,5 см в высоту. Каждый снимок был разделен на 100 полос по ширине, толщиной по 0,12 см, задана точность ε=0,01.
При помощи ЭВМ были вычислены площади каждой из полос
Si1,Si2 и найдены средние значения длины yi и высоты полос zi. Для ускорения вычислений, вначале вычисляются периметр каждого из сечений по формуле Piс 2(yi zi ), складываются, и по конечному результату вычисляется площадь поверхности тела, который рассчитывается путем умножения полученной суммы на ширину полосы Δx (т.к. она у всех полос одинаковая) и однократного деления на синус угла между проекциями. В итоге было получено:
n
Pic x
![]() S p i1 58050,12 721,5см2; sin sin75
S p i1 58050,12 721,5см2; sin sin75
Таким образом, полученные результаты позволяют констатировать, что предельное значение площади поверхности исследуемой печени добровольца приближается к 721,5 см2.
ЗАКЛЮЧЕНИЕ
Результаты вычислений площади поверхности и площадей проекций тела подтверждаются контрольными томографическими измерениями и дают преимущества в требовании минимального числа проекций исследуемого тела.
UDC 517.3 L.S. Kryzhevich e-mail: [email protected]
Kursk State University, Kursk
CALCULATION OF THE SURFACE POINT CLOUD, OBTAINED BY SCANNING EXAMINE LIMB
The article about mathematical aspects of numerical calculation of surface area limb, given the cloud of individual points, after his scan and create three-dimensional model
75
Keywords: surface area, 3D-model.
УДК 372.851
Д.А. Мелентьев1, К.А. Фильчакова2, Е.А. Башилова3 е-mail: [email protected]
1
ОБОУ «Школа-интернат № 4» города Курска
2,3
ФГБОУ ВПО «Курский государственный университет»
ИСПОЛЬЗОВАНИЕ МЕТОДА РАЦИОНАЛИЗАЦИИ ДЛЯ
РЕШЕНИЯ АЛГЕБРАИЧЕСКИХ НЕРАВЕНСТВ
ПРОФИЛЬНОГО ЕГЭ ПО МАТЕМАТИКЕ
Школьный метод решения алгебраических неравенств предусматривает переход к равносильной совокупности систем и необходимости решения большого количества неравенств, на которые распадается данное. Рассмотренный альтернативный метод менее трудоемкий и позволяет решать не только стандартные школьные неравенства, но и неравенства повышенной сложности, встречающиеся в заданиях профильного ЕГЭ.
Ключевые слова: метод рационализации, алгебраические неравенства.
Решение алгебраических неравенств обычно вызывает затруднения у многих обучающихся. Необходимо уметь разбираться с разными типами неравенств: рациональными, логарифмическими, показательными, степенными, что отражено в кодификаторе КИМ профильного ЕГЭ по математике. Необходимо владеть не только методом интервалов, но и некоторыми другими приёмами.
Существует метод, позволяющий избежать многие логические и вычислительные ошибки, ускорить процесс решения неравенств. Этот метод известен уже около 50 лет и в разных источниках фигурирует под названиями «метод декомпозиции», «метод замены множителей», «обобщённый метод интервалов», «метод рационализации».
Метод рационализации заключается в замене сложного выражения F(x) на более простое выражение G(x), при котором
76
неравенство G(x) > 0 равносильно неравенству F(x) > 0 в области определения выражения F(x).
Выделим некоторые выражения F и соответствующие им рационализирующие выражения G, где f x 0, g x 0, h x 0 – выражения, зависящие от x; px, q x – произвольные выражения, зависящие от x.
|
№ |
Исходное выражение F x |
Выражение после замены G x |
||||
|
1 |
logh x f x logh x g x h x 1 |
h x 1 f x gx |
||||
|
2 |
logh x f x 1 h x 1 |
h x 1 f x h x |
||||
|
3 |
logh x f x h x 1 |
h x 1 f x 1 |
||||
|
4 |
h x px h x q x |
h x 1 p x q x |
||||
|
5 |
|
px |
|
q x |
|
pxq x p x q x |
Рассмотрим конкретные задачи, которые дадут лучшее представление о том, как нужно применять метод рационализации. Задача 1. Решить неравенство:
logx2 x 21.
Решение.
Перейдём в данном неравенстве к новому основанию. Например, к основанию 10: lgx 2
![]() 2 1. lg x
2 1. lg x
Чтобы применить метод рационализации, нам в правой части необходим нуль. Переносим единицу влево и приводим к общему знаменателю:
lgx 2 lg x2
![]() 0.
0.
2
lg x
77
Видим, что в числителе получилась разность логарифмов, но не хватает разности логарифмов в знаменателе. Поэтому представим знаменатель в следующем виде: lg x2 lg x2 0 lg x2 lg1.
Таким образом, наше неравенство принимает вид:
lgx 2 lg x2
![]() 0 lg x2
lg1
0 lg x2
lg1
До сих пор мы совершали равносильные преобразования, так что полученное неравенство равносильно исходному неравенству.
Заметим, что в силу монотонного возрастания функции y lg x числитель совпадает по знаку с разностью x 2 x2, а
знаменатель совпадает по знаку с разностью x2 1.
Таким образом, мы воспользовались строкой № 1 таблицы часто встречающихся замен.
Поэтому неравенство равносильно системе:
x 2 x2
![]() 2 0,
2 0,
x 1
x 2 0,
2 x 0.
Преобразуем первое неравенство системы:
x 1x 2
![]() 0,
0,
x 1x 1
Данное неравенство решим методом интервалов: x 1, 1 x 1, x 2.
Решения второго и третьего неравенств системы – это множество
2 x 0, x 0.
Остаётся пересечь полученные множества. Ответ: 2; 1 1;00;1 2; .
Как видите, метод рационализации избавляет нас от необходимости рассматривать два случая (основание логарифма больше/меньше единицы).
Задача 2. Решить неравенство:
78
2x26 x24x
2 4 .
Решение.
Преобразуем неравенство в виду x23 x24x
4 4 .
Воспользуемся строкой № 4 таблицы замен. В нашем случае h x 4, p x x2 3, q x x2 4x.
Получим, что данное неравенство можно заменить на следующее выражение:
x2
3 x2
4x,
4x 3,
x
![]() 3;.
3;.
4
3 Ответ:
x ![]() ;
;
4
В заключение заметим, что изложенный здесь прием решения неравенств не является, разумеется, универсальным; он не всегда применим, не всегда сокращает и упрощает решение. С другой стороны, этими свойствами, очевидно, не обладает ни один из методов решения. В то же время круг применения рационализации представляется достаточно широким.
Список литературы
1. Иванов С.О., Ольховая Л.С., Ханин Д.И. Математика. Подготовка к ЕГЭ: решаем задания С3 методом рационализации: учебно-методическое пособие /Под ред. Ф.Ф. Лысенко. Ростов-на- Дону: Легион, 2013.
2. Дорофеев Г.В. Обобщение метода интервалов. // Математика в школе. 1969. № 3.
3. И.Я. Яковлев. Материалы по математике: подготовка к олимпиадам и ЕГЭ [Электронный ресурс]. – mathus.ru.
4. Кодификатор элементов содержания для составления КИМ для проведения в 2015 году профильного ЕГЭ по математике [Электронный ресурс]. Москва: ФИПИ, 2015.
D.A Melentev1, K.A Filchakova2, E.A Bashilova3 e-mail: [email protected]
1
OBOU "Boarding school № 4" of Kursk
2,3
FGBOU VPO "Kursk State University"
79
USING TO SOLVE RATIONALIZATION OF ALGEBRAIC
INEQUALITIES PROFILE EGE IN MATHEMATICS
School method of solving algebraic inequalities calls for a shift to an equivalent set of systems and the need to address the large number of inequalities, which breaks this. Considered an alternative method is less time consuming and can solve not only standard school inequality, but inequality increased complexity encountered in EGE profile jobs.
Key words: method of rationalization algebraic inequalities.
УДК 378.1
О.А. Мокеева1, С.А. Мокеева2
1
Белорусский государственный университет информатики и радиоэлектроники, Минск (Республика Беларусь)
2
Белорусский государственный университет, Минск (Республика Беларусь)
ПОДХОД К ОРГАНИЗАЦИИ ОБУЧЕНИЯ СТУДЕНТОВ
ЗАОЧНОЙ ФОРМЫ ПОЛУЧЕНИЯ ОБРАЗОВАНИЯ
ПРИ ИЗУЧЕНИИ МАТЕМАТИЧЕСКИХ ДИСЦИПЛИН
В статье говорится об организации учебного процесса при заочной форме обучения при изучении математических дисциплин
Ключевые слова: заочная форма, студенты, математические дисциплины, форма контроля, организация, пример, решение.
Для студентов заочной формы получения образования знакомство с новой дисциплиной начинается с установочной лекции, которая закладывает основы понимания студентами сущности знаний, а главное, отношение к этим знаниям, направляет пути и способы их приобретения. Целью ее является оказание помощи студентам-заочникам в организации самостоятельного овладения дисциплиной.
80
Необходимо создать необходимую учебно-методическую базу; обеспечить консультационно-методическую помощь профессорско-преподавательского состава.
На установочной сессии по математическим дисциплинам преподаватели знакомят студентов с требованиями, предъявляемыми к изучаемым дисциплинам, а именно: какой теоретический материал должен знать студент по каждому из имеющихся разделов, какой сложности задачи он должен уметь решать, какие формы контроля его ждут.
Сравнительно небольшое количество учебного времени, предусмотренного учебным планом на изучение дисциплин, обуславливает краткое, насыщенное изложение учебного материала.
Преподаватель дает обзор учебников и учебных пособий, специальной литературы по проблематике курса, а также знакомит с работой, которая будет организована на кафедре в помощь студентам. В электронном читальном зале есть электронные версии необходимых методических пособий и учебно-методических комплексов (ЭУМК).
В межсессионный период на кафедре организованы консультации. В дни заочника установлено дежурство преподавателей. В эти дни студенты могут получить квалифицированную помощь по любому из интересующих их вопросов. Попытки, когда студент ничего не зная и не открывая учебной литературы, приходит на консультацию и «учите его», сразу же прерываются. На установочной сессии всех предупреждают, что консультацию можно получить только по конкретным вопросам. Главное значение консультации в том, чтобы корректировать умение студента прорабатывать учебную литературу самостоятельно, научить обобщать полученную информацию и использовать ее при решении задач.
При разработке методических пособий для студентов заочной формы получения образования необходимо руководствоваться следующими принципами: доступность, конкретность и ясность.
Методическое пособие составляется в соответствии с учебной программой математической дисциплины. Указывается список рекомендуемой литературы. Весь материал разбивается на пункты. В начале каждого пункта приводятся необходимые теоретические сведения и примеры с подробными решениями. Для закрепления материала составляются задачи для самостоятельного решения и 10
81
вариантов заданий для индивидуальной работы студентов, тестовые задания. К тестам даны ответы. Приведенные вопросы для самоконтроля позволяют организовать контроль знаний при самостоятельной работе и подготовиться к выполнению индивидуальных заданий. В приложениях содержатся уравнения и графики, формулы и таблицы.
Когда студенты приезжают на экзаменационную сессию, то на лекциях и практических занятиях идет процесс закрепления и обобщения уже имеющихся знаний. Студенты выходят на экзамен (зачет) более подготовленными.
Следует отметить, что творческий подход к построению занятий, его неповторимость, насыщенность многообразием приемов, методов и форм могут обеспечить эффективность учебного процесса для студентов заочной формы.
Применение ИКТ на занятии становится очень распространенным явлением. Правильное использование в учебном процессе компьютера, позволяет осуществлять учебный процесс в новых условиях. Так как сокращается количество аудиторных часов, то в процессе изучения математических дисциплин можно использовать компьютер как вспомогательное средство, что позволит проверить решения задач, которые требуют рутинных трудоемких операций. В настоящее время разработаны математические пакеты: Maple, MathCAD, MathLAB, Mathematica и др. Они имеют существенные различия, но направлены на достижение общей цели – освободить студента от трудоемких операций при решении задач, и позволяют сократить время получения результата.
Например, система Mathematica проводит сложные символьные преобразования и является одной из самых мощных и эффективных компьютерных математических систем. C помощью системы Mathematica можно решать задачи линейной алгебры, математического анализа, задачи теории чисел и статистики, дискретной математики, а также проводить вычисления с любой заданной точностью, т. е можно использовать как «калькулятор». Сильной стороной данной системы является развитая двух- и трехмерная графика, которая применяется для вычерчивания кривых и изображения поверхностей по их уравнениям.
82
На практических и лабораторных занятиях по дисциплине «Прикладная математика» студенты с помощью системы
Mathematica могут проверить правильность решения задач.
Пример 1. Вычислить ÍÎÄ 96,165. С помощью расширенного алгоритма Евклида найти целые числа u и v, удовлетворяющие соотношению Безу: au bv ÍÎÄ a,b.
Решение. 1) Составим алгоритм Евклида для чисел 165 и 96, последовательно выполняя деление с остатком:
165 961 69,
96 691 27,
69 27215,
27 15112, 15 121 3, 12 34.
Последний отличный от нуля остаток в алгоритме Евклида является ÍÎÄ 96,165, т. е. 3.
2)Чтобы выразить ÍÎÄ 96,165 через исходные числа, будем двигаться в алгоритме Евклида снизу вверх, последовательно выражая остатки:
ÍÎÄ (96,165) 3 1512 15 (27 15) 215 27
2(69 272) 27 269527 269 5(96 69) 769 596 7(165 96) 596 71651296.
Поэтому 3 96(12) 7165.
3)В системе Mathematica при помощи функции ExtendedGCD165,96 получим ответы решения задачи: 3,12,7.
Пример 2. Найти остаток от деления числа 293175на число 48.
Решение. 1) Для нахождения остатка воспользуемся свойствами сравнений.
293 5(mod48),
293175 5175(mod48).
Так как 53 29(mod48), то 5175 55358 52958(mod 48).
Поскольку 292 25(mod48), то 529229 52529(mod 48). Так как
252 1(mod48), то 525214 25 5114 25(mod 48).
Итак, 293175 125(mod48). Поскольку 125 29(mod 48), то
293175 29(mod48), то есть остаток при делении числа 293175на число 48 равен 29.
83
2) В системе Mathematica с помощью функции
Mod293^175,48 получим ответ 29.
Использование компьютера в обучении математических дисциплин позволяет устанавливать и укреплять межпредметные связи математики и информатики. Это способствует активному включению студента в учебный процесс, поддерживать интерес, способствует пониманию и запоминанию учебного материала, развитию логического и пространственного мышления, что развивает и формирует личность будущего специалиста.
Промежуточной формой контроля может быть тестирование (или компьютерное тестирование). Тесты проверяют первичные знания и выступают как допуск к экзамену (зачету). Весь материал, выносимый на экзамен (зачет), разбивается на блоки, каждый из которых содержит от 10 до 30 тестовых заданий. Вопросы в этих заданиях сформулированы кратко и четко, содержат 5 вариантов ответов, один из которых правильный. Студентам предлагается за 20 минут выполнить 10 заданий. Тест сдан, если студент выполнил не менее 40% предложенных заданий, то есть правильно ответил на 4 и более вопросов.
В процессе сдачи тестов (особенно, если с первой попытки не сдали) студенты повторяют пройденный материал, обобщают и переосмысливают его. Ведь сдача тестов – единственный путь к экзамену (зачету), ограничение во времени не дает возможности воспользоваться шпаргалками, и, в конце концов, приходится взяться за учебник.
Тестовая форма контроля выполняет также развивающую функцию. Ведь от студента, сидящего перед монитором, требуется организационная и психологическая мобилизация, ответственность, организация умственного труда, обострение внимания, тренировка памяти, воспитание воли.
В помощь студентам для сдачи теста предлагаются вопросы, примерные тестовые задания и методические пособия.
Сдав тестирование, студент выходит на итоговую форму контроля знаний – экзамен (зачет).
Организация учебного процесса для студентов заочной формы получения образования должна не только побуждать студента работать самостоятельно, но и должна быть построена таким образом, чтобы студент сам стремился к самообразованию.
84
О.А. Mokeeva1, S.А. Mokeeva2
1
Belarusian State University of Informatics and Radioelectronics, Minsk (Republic of Belarus)
1
Belarusian State University, Minsk (Republic of Belarus)
APPROACH TO THE ORGANIZATION OF TRAINING OF
STUDENTS OF THE CORRESPONDENCE FORM
OF EDUCATION WHEN STUDYING MATHEMATICAL
DISCIPLINES
In article it is told about the organization of educational process at tuition by correspondence when studying mathematical disciplines.
Key words: correspondence form, students, mathematical disciplines, control form, organization, example, decision.
85
УДК 378.1
О.А. Мокеева1, С.А. Мокеева2
1
Белорусский государственный университет информатики и радиоэлектроники, Минск (Республика Беларусь)
2
Белорусский государственный университет, Минск (Республика Беларусь)
ОРГАНИЗАЦИЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
СТУДЕНТОВ
Статья посвящена подробному описанию видения организации самостоятельной работы студентов авторами статьи.
Ключевые слова: организация, учебный процесс, студент, математические дисциплины, самостоятельная работа студентов.
Развитие и образование ни одному человеку не могут быть даны или сообщены. Всякий, кто желает к ним приобщиться, должен достигнуть этого собственной деятельностью, собственными силами, собственным напряжением.
А. Дистервег
Первостепенным вопросом современного образования является подготовка специалистов завтрашнего дня, конкурентноспособных, умеющих творчески и оперативно решать нестандартные задачи. Преподаватель математики призван обучать и воспитывать студентов, развивать интерес к изучаемой дисциплине, которая дает большой эффект в формировании математических знаний и способствует активизации процесса восприятия знаний и мыслительной деятельности. Для этого преподаватель должен использовать в своей работе разнообразные методы, приемы и средства методической коммуникации, должен не только уметь изложить материал, но и всемерно содействовать студентам в приобретении навыков самостоятельной работы над теми материалами, которые непосредственно связанны с содержанием основного курса, но находятся за пределами, предусмотренными программой.
86
Цель учебного процесса заключается не только в передаче знаний, умений и навыков от преподавателя к студенту, но и в развитии у студентов способности к самообразованию. Студента следует рассматривать как активную фигуру учебного процесса, а не пассивный объект обучения. Поэтому необходимо включать его в активную учебную деятельность, «учить учиться», оказывать ему помощь в приобретении знаний.
Самостоятельная работа студентов является одной из форм подготовки образованной, творческой и профессиональномобильной личности. Существуют различные приемы, которые можно использовать для оживления самостоятельной работы студентов по дисциплине. Важно вовлечь студентов в процесс подготовки, заинтересовать, оживить чувство интереса. Умело организованная и методически грамотно построенная самостоятельная работа расширяет и углубляет знание студентов, развивает у них математические способности и математическое мышление, расширяет и углубляет представления о практическом применении математики в различных областях науки. При организации любого вида самостоятельной работы должен быть контроль и оценка результатов выполнения учебной деятельности студентов. Если работа не проверяется, то у студентов пропадает интерес к ней, что приводит к снижению положительной учебной мотивации в целом.
Внедрение в учебный процесс самостоятельной управляемой работы студентов (СУРС) ставит следующие задачи: способствовать развитию у студентов стремления к постоянному пополнению и обновлению знаний и умений; формировать способность студентов осмысливать и обобщать учебный материал; разнообразить формы и методы обучения. Формы организации СУРС могут быть разными, в зависимости от дисциплины и объема часов, определенных учебным планом. Для обеспечения эффективности необходимо установить рациональное соотношение между СУРС и аудиторными занятиями; создать необходимую учебно-методическую базу; обеспечить консультационно-методическую помощь профессорскопреподавательского состава. Внедрение СУРС в учебный процесс стимулирует студентов к работе с необходимой литературой, вырабатывает навыки принятия решений.
На первом курсе студенты изучают дисциплину «Математика». Не всегда на лекции и практическом занятии есть время пока-
87
зать внутреннюю красоту самой математики, остановиться на ее истории, более подробно рассмотреть приложения. Для решения этой проблемы и чтобы «не потерять» способных студентов, а также, чтобы «не отбить охоту» у тех, кто желает расширить и обогатить свои знания, на кафедре необходимо проводить математический кружок. Посещение кружка стимулирует интерес к дисциплине, развивает творческое мышление, логику рассуждения, пространственное воображение, сообразительность и упорство в достижении цели, научную интуицию. Кружковая работа в дальнейшем перерастает в научную работу. Студенты с «охотой» принимают участие в научных конференциях, межвузовских и республиканских олимпиадах. Участие в математических конференциях вырабатывает у студентов творческий подход к освоению внепрограммного материала, дает возможность проявлять свои математические способности в нестандартной учебной ситуации, вызывает интерес к изучению дополнительной математической литературы, как у докладчиков, так и у слушателей.
Внутривузовская математическая олимпиада в силу присущего ей яркого соревновательного характера не только решает задачу выявления наиболее одаренных и подготовленных студентов, но и привлекает к дополнительным занятиям по подготовке к олимпиадам большое число студентов, побуждает их к углубленному изучению математики. Олимпиадные задания требуют от участников оригинальных, глубоких математических решений. Удачное выступление на олимпиаде служит для студентов мощным стимулом для дальнейшего совершенствования математической подготовки и участие в межвузовских и республиканских олимпиадах. Олимпиады заставляют трудиться всерьез, самостоятельно обдумывать трудные ситуации, приучают к творчеству.
Примером самостоятельной работы может быть выполнение индивидуальных домашних заданий в течение месяца. Данные задания оцениваются, так как в вузе модульно-рейтинговая система обучения.
Модульно-рейтинговая система обучения и оценки успеваемости студентов представляет собой комплексную систему поэтапной оценки уровня освоения обучаемым учебной дисциплины образовательной программы высшего образования по специальности, направлению специальности, при которой осуществляется структу-
88
рирование содержания каждой учебной дисциплины на модули и проводится регулярная оценка знаний и умений студента в течение семестра. В данной системе все знания, умения и навыки, приобретаемые студентом в процессе изучения дисциплины, оцениваются рейтинговыми баллами. Рейтинговые баллы набираются в течение всего периода изучения обучаемым учебной дисциплины и фиксируются путем занесения в ведомость учета рейтинговых баллов студента. Рейтинговая система имеет целью поставить студента перед необходимостью регулярной учебной работы в течение семестра, развитию стремления к постоянному, непрерывному самообразованию, обновлению знаний и творческому использованию их на практике. Текущий контроль осуществляется в течение семестра один-два или более раз в семестр в зависимости от объема изучаемой дисциплины, который может осуществляться в виде письменных работ, тестов, рефератов, в форме коллоквиумов, устных фронтальных опросов и др. Итоговый контроль представляет собой зачет или экзамен в сессионный период по дисциплине в целом. Рейтинговая оценка по дисциплине является интегральным показателем, формируемым на основе оценки знаний студента в ходе текущего и итогового контроля. Она включает оценки, полученные студентами на практических и лабораторных занятиях, а также оценки по всем видам отчетности контролируемой самостоятельной работы студентов и итоговую оценку. Вклад текущего контроля в рейтинговую оценку знаний по дисциплине может достигать 70%. Оценки по всем видам отчетности выставляются по 10-балльной шкале.
Целями внедрения модульно-рейтинговой системы являются:
– повышение мотивации и активизация самостоятельной деятельности студента по изучению учебных дисциплин образовательной программы высшего образования по специальности, направлению специальности в течение семестра;
– повышение качества обучения за счет интенсификации учебного процесса, активизации работы профессорскопреподавательского состава по совершенствованию содержания и методов обучения.
Для каждого модуля устанавливается перечень обязательных видов учебной работы студента, определяемый рейтинг-планом дисциплины и предполагающий отметки в 10-балльной системе
89
(например, отметки, полученные на лекциях, практических (лабораторных) занятиях; за выполнение контрольных и типовых расчетов; написание рефератов; участие в коллоквиумах; тестирование по теме (группе тем); другие виды работ).
Рассмотрим самостоятельную работу студентов. По дисциплине «Математика» при выдаче очередного типового расчета (индивидуальных домашних заданий), группу студентов делят на 5 команд по 6 человек, каждой команде необходимо выполнить 5 заданий. Все команды должны за занятие рассказать решения всех задач. Задания сложные и очень трудно за короткое время ознакомить с решениями всех задач. Команды решили сделать презентацию их работы с оригинальными решениями задач. Все задания представлены с рисунками и звуковой аннимацией. Например, одна команда провела презентацию работы в виде популярной телевизионной игры «Сто к одному», чтобы разнообразить студенческие будни, а также помочь всей группе студентов оценить свои знания по данным темам. Для дифференциации ответов по популярности они опросили студентов всего потока. Мультимедийная часть (игровое табло) была организована при помощи программы подготовки презентаций «Microsoft PowerPoint». В игре участвовали две команды, которые организованы на занятии среди студентов группы. В начале раунда от каждой из команд выходит один игрок, и ведущий задает вопрос. Существует 6 вариантов ответов. Ответы расположены на игровом табло. Команда, игрок которой ответил первым и правильно, продолжает отгадывать. В случае, если игрок угадал не самый популярный вариант, право ответа предоставляется другой команде. Далее каждому игроку этой команды по очереди задается вопрос и его ответ проверяется на игровом табло. Вторая команда ждет, когда первая команда ответит неверно 3 раза, и право ответа перейдет к ним. Эта команда может предложить только один вариант ответа, и если их ответ окажется на табло, то они получат все баллы, которые первая команда получила в этом раунде и т. д.
Использование компьютера в обучении математических дисциплин позволяет устанавливать и укреплять межпредметные связи математики и информатики. Это способствует активному включению студента в учебный процесс, поддерживать интерес, способст-
90
вует пониманию и запоминанию учебного материала, развитию логического и пространственного мышления.
Организация учебного процесса должна не только побуждать студента работать самостоятельно, но и должна быть построена таким образом, чтобы студент сам стремился к самообразованию. Для получения глубоких и прочных знаний нужен систематический, целеустремленный, каждодневный, упорный и серьезный труд. Творческий подход к построению занятий, его неповторимость, насыщенность многообразием приемов, методов и форм могут обеспечить эффективность учебного процесса.
О.А. Mokeeva1, S.А. Mokeeva2
1
Belarusian State University of Informatics and Radioelectronics, Minsk (Republic of Belarus)
1
Belarusian State University, Minsk (Republic of Belarus)
ORGANIZATION OF INDEPENDENT WORK OF STUDENTS
Article is devoted to the detailed description of vision of the organization of independent work of students by authors of article.
Key words: organization, educational process, student, mathematical disciplines, independent work of students.
91
УДК 330.45
Н. А. Моргунова, Е. Ю. Моргунова e-mail: [email protected]
Юго-Западный государственный университет, г.Курск
РЕШЕНИЕ ЗАДАЧИ О МИНИМИЗАЦИИ ЦЕЛЕВОЙ
ФУНКЦИИ
В данной статье решается задача линейного программирования о минимизации целевой функции с помощью табличного процессора MS Excel.
Ключевые слова: математическое моделирование, поиск решения, целевая функция, система ограничений.
Чтобы хорошо разбираться в вопросах моделирования экономических ситуаций современный экономист должен не только иметь теоретическую подготовку в области математики и экономики, но и владеть навыками построения экономико-математических моделей, знать компьютерные технологии, подходы и методы к решению экономических задач.
Методы решения оптимизационных задач наиболее распространены. Их называют методами математического программирования. К этим методам, в частности, относятся задачи линейного программирования.
Для того чтобы решить оптимизационную задачу, необходимо построить целевую функцию F(Х), систему ограничений и найти оптимальное решение.
Такая задача не всегда является разрешимой. Например, задача максимизации будет неразрешимой, если целевая функция F(Х) не ограничена сверху на допустимом множестве U.
Решение задач линейного программирования графическим методом, симплекс-методом или иным другим будет тем более громоздким, чем больше переменных и неравенств в системе ограничений. В связи с этим целесообразно использовать компьютерные технологии.
Пусть требуется решить задачу линейного программирования о минимизации следующей целевой функции:
92
F(х1, х2) = 7х1 + 2х2 → min
при неравенствах ограничений
2x1 + 3x2 ≥ 8,
4x1 + 2x2 ≥ 11, x1 + 4x2 ≥ 12, 2x1 + 3x2 ≥ 10, x1 ≥ 1, x1 ≥ 0, x2 ≥ 0.
Используем при решении табличный процессор MS Excel. В нем имеется надстройка Поиск решения, которая вызывается из меню Сервис. Если она не найдена, то в окне Надстройки, появляющемся после выполнения команд Сервис→Надстройки, необходимо установить флажок Поиск решения.
С помощью процедуры Поиск решения можно находить оптимальное из допустимых решений, задавать ограничения сложного вида, получать множество решений и генерировать их, а в дальнейшем сохранять эти решения в виде сценариев.
В основе надстройки Поиск решения лежит симплекс-метод.
Запустим табличный процессор MS Excel
(Пуск→Программы→Microsoft Office→Microsoft Office Excel). Введем исходные данные на рабочий лист.
В ячейку В10 введем формулу СУММПРОИЗВ(B9:C9;B8:C8). В ячейку D3 скопировать формулу из ячейки В10, заменив диапазон B9:C9 на диапазон параметров B3:C3. В результате, в ячейке Е3 получится формула СУММПРОИЗВ(B3:C3;B8:C8). Для задания остальных ограничений скопируем данную формулу в ячейки D4, D5, D6, D7.
93
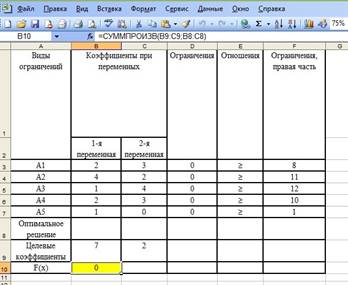
Рис. 1. Исходные данные
Создав таблицу, установим курсор в ячейку В10 и выберем в меню Сервис функцию Поиск решения. Заполним поля в появившемся окне и нажмем кнопку "ОК".
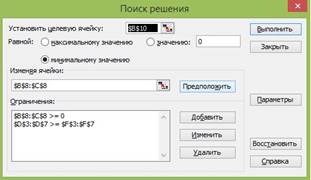
Рис. 2.Окно "Поиск решения"
94
После заполнения всех полей окна нажмем кнопку "Параметры" и в открывшемся окне "Параметры поиска решения" установим флажки "Линейная модель" и "Неотрицательные значения".
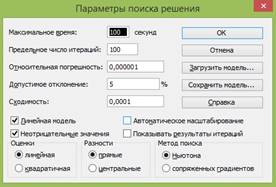
Рис. 5. Окно "Параметры поиска решения"
Задав все параметры, нажмем кнопку "Выполнить". Если решение существует, то появится окно с соответствующим сообщением.
95
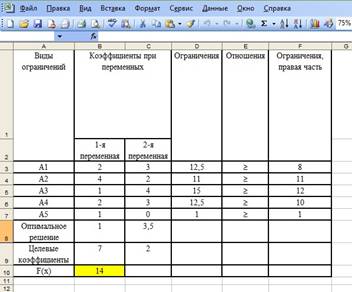
Рис. 5. Полученное решение задачи
Таким образом, минимальное значение целевой функции равно 14 при х1=1 и х2=3,5.
Подводя итоги исследования, отметим, что использование табличного процессора MS Excel возможно и при решении задач максимизации целевой функции.
Таким образом, с помощью данного метода можно решать следующие экономические задачи:
• на определение оптимального ассортимента продукции;
• на составление оптимального плана работы групп оборудования, при котором будет выполнен план выпуска продукции с минимальной себестоимостью в заданный срок;
• на составление суточного рациона, содержащего множество питательных веществ и обеспечивающего минимальную общую стоимость закупаемых продуктов;
• на выбор портфеля ценных бумаг;
• на оптимальный раскрой (минимизацию обрезков);
96
• на оптимальное распределение потоков товарных поставок по транспортной сети и др.
Результаты решения задач в MS Excel можно сохранять в виде листов "Отчет по результатам", "Отчет по устойчивости", "Отчет по пределам".
__________________________________________
1. Невежин В. П., Кружилов С. И. Сборник задач по курсу "Экономико-математическое моделирование". М.: Городец, 2005.
320 с.
N. A. Morgunova, E. Yu. Morgunova e-mail: [email protected] South-West State University, Kursk
DECISION OF A TASK OF MINIMIZING OF THE OBJECTIVE
FUNCTION
In this article a task of linear programming about minimization of the objective function is decided using the table processor MS Excel.
Keywords: mathematical modeling, search for solutions, the target function, the system of restrictions.
УДК 373:51
Е.А. Осипова
Частное учреждение Средняя общеобразовательная школа
№Потенциал», Москва e-mail: [email protected]
ПРОБЛЕМА ПРЕЕМСТВЕННОСТИ ОБУЧЕНИЯ
ШКОЛЬНИКОВ В НАЧАЛЬНОЙ И ОСНОВНОЙ ШКОЛЕ
Статья посвящена сложной актуальной проблеме преемственности обучения школьников в начальной и основной школе. Вопросы, на которые сделан акцент, затрагивают содержание школьного курса, способы изложения этого содержания, формы и методы организации учебного процесса, изменение стиля отноше-
97
ний между учащимися и учителями и их влияние на успешность последующего обучения.
Ключевые слова: математика, преемственность, школа.
В связи с вариативностью образовательных систем сегодня особенно остро встала проблема согласования технологии и учебного содержания при переходе от одной образовательной программы к другой как по вертикали, так и по горизонтали.
Таблица показывает, имеется ли преемственность (хотя бы по содержательной линии) в создании единого образовательного пространства при изучении математики в 5-х классах.
|
Система обучения в начальной школе |
Система обучения в 5 классе |
Количество учащихся (%) |
|
Традиционная |
Традиционная |
61 |
|
Развивающая |
Развивающая |
15 |
|
Развивающая |
Традиционная |
24 |
Первая строка таблицы показывает, что 61% учеников как обучались в начальной школе, так и продолжают в основной обучаться по традиционным учебникам традиционными способами.
Из 39% выпускников начальной школы только 15% продолжают обучение по учебно-методический комплекс (УМК), относимым к учебникам развивающего характера: Л.Г. Петерсон - 8% (в начальной школе было 26%), Г.В. Дорофеев - 3%, СМ. Никольский
- 3%.
Самую большую тревогу вызывают показатели последней строки: таблицы: из 39% выпускников начальной школы большая часть - 24% -переводится в 5-й класс на традиционное обучение по традиционным УМК (по учебникам Н.Я. Виленкина обучается 49% всех пятиклассников, по учебникам И.Б. Барановой - 32%, и даже по морально устаревшим учебникам Э. Нурка - 5%), и это больше, чем по современным учебникам Г.В. Дорофеева или С.М. Никольского. Именно в таких классах остро стоит проблема преемственности и в обучении, и в развитии. При обучении в 5-м классе 24% учащихся могут испытывать и действительно испытывают дискомфорт из-за того, что их учат на уроке работать не так, как они уже умеют, что им не хватает пищи для ума - значительная часть со-
98
держания программы 5-го класса знакома или уже усвоена ими в начальной школе. [5]
И первый вопрос, который необходимо поставить, - необходимость учета принципов систематичности и последовательности в процессе обучения математике. То есть изучение тем курса математики необходимо выстроить так, чтобы в явном виде осуществлялась опора на материал, ранее усвоенный младшими школьниками, и активно осуществлялись связи между изучаемым и изученным учебным материалом.
«Преемственность требует повторения, но такого повторения, которое обеспечивает непрерывное развитие системы понятий, а не повторения ради повторения, ради сохранения на достаточно высоком уровне некоторых навыков учащихся. Если мы хотим, чтобы преемственность осуществлялась по существу, а не по форме, то повторение должно быть органически включено в новую тему и по мере развития темы должно соответственно меняться, не сводясь к механическому повторению одних и тех же упражнений» [1, с.14]. Для создания целостного представления об изучаемом предмете у учащихся необходимо в процессе обучения осуществлять систематическое повторение учебного материала, причем как материала, усвоенного ранее и связанного каким-либо образом с данным уроком, так и с материалом предшествующих лет обучения. При этом необходимо учитывать тот факт, что повторение не должно сводиться только к механическому повторению известных фактов и упражнений, а должно быть органично включенное в изучаемый материал. Согласно рассматриваемому подходу на каждом последующем этапе повторения в известном учебном материале и упражнениях появляется нечто новое, а старое, неважное для данного уровня образования обучаемых отмирает, что определяется логикой формирования изучаемого понятия. По мнению Константина Ивановича Нешкова, осознание понятия «преемственность» позволяет выявлять важные части изучаемого материала и располагать их в таком порядке, чтобы процесс обучения способствовал развитию мысли ученика с учетом выявленных взаимосвязей отдельных этапов и частей этого процесса.
Известный математик и методист А.Я. Хинчин определил шесть видов повторения используемых в обучении школьников: повторение в начале учебного года; текущее повторение, проводи-
99
мое в процессе урока; повторение темы, связанное с проведением учета; повторение годовое и др. Известно, что сам автор к данному перечню видов повторения дал такой комментарий: «Кошмар! Вместо бесконечных повторений нельзя ли учить так, чтобы материал не забывался?»[2, с.69].
Второй вопрос преемственности обучения заключается в том, что процесс обучения математике в начальном звене и пятом, шестом классе должен представлять собой процесс подготовки к обучению таким разделам школьного курса математики, как алгебра и геометрия. [3]
Перед учителем в 5-6 классе ставится задача обобщения и развития на новом материале полученных в начальной школе математических знаний, умений и навыков. Большинство понятий в этом курсе вводятся на примерах, но сохраняется индуктивный характер изложения материала. Математические суждения делаются, исходя из наглядного рассмотрения и опытного обоснования, использования и обобщения жизненного опыта учащихся. При доказательстве свойств арифметических действий, геометрических фактов, признаков делимости используется аналогия. Но всё чаще на уроке проводятся дедуктивные рассуждения. Учащимся даётся возможность почувствовать логику рассуждений и отличие дедуктивных доказательств от эксперимента.
На этих уроках важным и всенепременным является развитие речи учащихся в классе (рассуждения). Школьники должны объяснять действия вслух, разъяснять свои мысли, ссылаться на известные правила, высказывать догадки, предлагать способы решения. Необходимо поощрять учеников к этому. Желательно, чтобы вопросы и замечания типа «Почему?», «Как можно объяснить?», «Как ты думаешь?» постоянно звучали на уроках.
«В начальной школе должна быть заложена основа не только предметного знания, но и знания о собственном незнании.
Если ученики на протяжении всего начального обучения будут предъявлять учителю только свои знания и всячески ограждаться от встречи с ситуациями, где их знания вступают в противоречие с новыми фактами, то в основной школе умение учиться станет достоянием немногих избранных.
100
Поисковые действия, необходимы для приобретения недостающих умений, знаний, способностей, для ответа на второй вопрос самообучения: как научиться.
Этот вопрос имеет три ответа, три способа выйти за пределы собственной компетентности:
• самостоятельно изобрести недостающий способ действия, то есть перевести учебную задачу в творческую, исследовательскую, экспериментальную;
• самостоятельно найти недостающую информацию в любом
"хранилище", прежде всего - в книгах и Интернете;
• запросить недостающие данные у знатока и умельца.
Умение работать с книгой и прочими источниками информации может быть сформировано весьма рано, но не на первых шагах обучения: дети должны по крайней мере выучиться читать. Систематическое освоение этого способа расширения собственной компетенции - задача основной школы» [7]
Поэтому, третий аспект преемственности обучения выражается в том, что процесс обучения математике в начальной и основной школе сопряжен с необходимостью формирования у школьников умения и желания обучаться. [3]
Важнейшим условием, позволяющим правильно строить учебный процесс, сделать обучение эффективным, доступным, является чёткое дифференцирование материала. Учителю необходимо вычленять те задачи, которые должны отрабатываться и выполняться многократно, и те, которые служат другим целям (развитию познавательных интересов) и в соответствии с этим не должны дублироваться. Такое различие следует сделать явным и для самих учащихся. В первой четверти пятого класса необходимо повторять те вопросы, знание которых должно быть доведено до автоматизма.
1. Это счёт (в том числе и обратный) десятками, сотнями и
т.п., таблицы сложения и умножения однозначных чисел, тренировка памяти на удержание в уме промежуточных результатов вычислений (36:9+ 77:7).
2. Подбор примеров для повторения письменных арифметических действий должен провести учеников от простых случаев, включающих собственно умение выполнять алгоритм, до сложных,
101
с постепенным увеличением числа «запоминаний» и «заниманий» единицы.
3. Решение текстовых задач составляет значительную часть деятельности школьников при изучении математики. Поэтому следует извлекать из этой работы как можно больше пользы в плане обучения и развития. Полезный приём, который следует практиковать, - предлагать детям пересказывать условие задачи своими словами. Когда встречаются трудные задачи необходимо зрительно представить их с помощью рисунка, модели. Это помогает лучше уяснить связи между данными, удержать условие в памяти. Следует поощрять решение задачи разными способами, выясняя различия в ходе рассуждения. Полезно также предлагать детям придумывать задачи, добавлять вопросы и задания: «А что ещё можно было бы узнать?» Каждая задача может стать предметом обсуждения. [4]
Организуя учебный процесс, нужно постоянно иметь в виду своеобразный «принцип ножниц»: в процессе обучения использовать, хотя и доступный, но весьма широкий и разнообразный учебный материал. Учебная деятельность должна быть богатой по содержанию, требовать от школьников интеллектуального напряжения. В то же время обязательные требования, особенно на первых порах, должны быть очень невелики по охвату материала и доступны детям. Важно, чтобы школьники поверили в свои силы, испытали успех в учёбе. Именно учебный успех в этом возрасте может стать сильнейшим мотивом, вызывающим желание учиться.
Интересна в этом отношении книга В.А. Сухомлинского «Разговор с молодым директором школы». В ней он перечисляет 12 важнейших умений, которыми ученик должен овладеть в течение 10 лет. Вот некоторые из них:
5)Думать, сопоставлять, сравнивать несколько объектов, предметов, явлений.
6)Выделять логически законченные части в прочитанном, устанавливать взаимосвязь и взаимозависимость между ними.
7)Находить в книге материал по интересующему вопросу.
8)Делать предварительный анализ текста в процессе чтения.
11) Читать текст и одновременно слушать инструктаж учителя о работе над текстом, над логическими составными частями.
102
В заключении приведем таблицу, в которой сформулированы некоторые проблемы преемственности в преподавании математики между начальной школой и 5-м классом и возможные пути их решения. [6]
|
Проблема |
Тенденция |
Возможности разрешения |
|
Организационно-психологические |
||
|
Недостаточная наполненность урока учебным материалом, неоправданно медленный темп урока, отсутствие материалов для «сильного» ученика, перенос основной тяжести усвоения курса на домашнюю работу |
ухудшение
ситуации |
Уменьшение доли фронтальных бесед и др. малоэффективных методов работы на уроке, использование раздаточных дидактических материалов, уменьшение пауз в работе детей |
|
Недостаточно организованное и четкое начало урока, окончание урока, выделение дополнительного – сверх отведенных 45 мин – времени на выполнение письменных проверочных работ, из-за чего дети не приучаются быстро включаться в работу, эффективно и быстро работать |
ухудшение ситуации |
Приучить детей начинать работу на уроке по звонку, быстро включаться в работу, не давать отдельным детям дополнительного времени на выполнение контрольных и др. проверочных работ, заканчивать урок также по звонку конца урока |
|
Стойкая привычка у детей к неумеренной помощи родителей при выполнении домашних заданий, творческих работ |
стабильное положение
|
Разъяснение родителям наносимого ущерба интеллектуальному развитию их ребенка, включение в уроки заданий, контролирующих степень самостоятельности школьников в выполнении домашних заданий |
|
Бедность арсенала и однообразие используемых методов обучения, несоответствие методического багажа учителя реальным учебным возможностям детей |
ухудшение
ситуации |
Распространение опыта успешного обучения детей в современных условиях, (школьным методическим объединениям учителей начальных классов и математики, кафедрам полезно создавать «видеобиблиотеки» методов обучения для ознакомления с лучшим опытом) |
|
Пассивность большинства учащихся в процессе обучения |
стабильное положение |
Использование форм и методов организации занятий, требую- |
103 104
|
|
|
щих от каждого ученика активного и осознанного участия (в т.ч. парной, групповой работы) |
|
ти и анализировать его |
|
выполнении заданий по математике |
|
|
Недостаточная скорость письма, нечеткий почерк у значительной части детей |
стабильное положение
|
Рекомендовать упражнения для развития мышц кисти руки, подходящую ручку, продолжать следить за правильностью написания букв и цифр, за верным положением ручки |
|||||
|
Несформированность у учащихся представления об отличном устном ответе, ответе у доски на уроке математики (эталона ответа) |
ухудшение ситуации |
Учителям математики совместно с учителями начальной школы определиться в требованиях к ответу ученика и постепенно разъяснять детям эти требования, учитывать их, оценивая ответы на уроке |
|||||
|
Неустойчивость внимания, слабо развитая оперативная память у многих детей |
сильное ухудшение ситуации |
На уроках предлагать цепочные вычисления, дoма (под руководством родителей) – специальные упражнения на тренировку внимания и памяти |
|||||
|
Привычка у детей получать отметки за любое – самое малое – действие, в т.ч. за краткие или односложные, невразумительные ответы |
стабильное
положение
|
Добиваться от детей развернутых, полных ответов, четкой и грамотной речи; не допускать выставления необоснованно высоких отметок за неполные ответы |
|||||
|
Недостаточная тренированность долговременной механической памяти |
ухудшение ситуации |
Практиковать письменный опрос правил, предлагать для запоминания не только стихотворные, но и прозаические тексты |
|||||
|
Обедненная (вплоть до конца обучения в начальной школе) речь учителя, отсутствие динамики в использовании лексики от 1-го к 3-4-м классам, «сюсюканье» |
стабильное положение
|
Полезно создание и внедрение учителями математики совместно с учителями начальной школы словаря-программы постепенного ознакомления детей со «взрослой» лексикой, проведение отдельных уроков в начальной школе вместе с учителем средних классов |
|||||
|
Элементы псевдоучебной деятельности в процессе обучения, неумение отделять существенное от несущественного |
стабильное положение
|
Своевременно отходить от требований, предъявлявшихся детям на ранних этапах обучения, при первом знакомстве с учебным материалом |
|||||
|
Отсутствие у учащихся умения и привычки обращаться к энциклопедиям, справочникам, словарям, научно-популярной и дополнительной учебной литературе |
стабильное
положение
|
Рекомендовать иметь в классе справочные издания, предлагать учащимся задания по работе со справочниками и словарями, поручать готовить сообщения, рассказы, сочинения по материалам дополнительной литературы |
|||||
|
Создание у детей учителем и родителями в конце 4 (3)-го класса «психологического барьера» – настороженного ожидания трудностей учения в 5-м классе |
стабильное
положение
|
Знакомство родителей и детей со своими будущими учителями уже в 4(3)-м классе, проведение математических праздников, олимпиад, соревнований, отдельных уроков, родительских собраний совместно с учителем 5-го класса |
|||||
|
Специальные математические знания, умения и навыки |
|||||||
|
Недостаточные умения устных вычислений (все арифметические действия пределах 100 учащиеся должны выполнять устно) |
ухудшение
ситуации
|
Постоянное подкрепление знания таблиц сложения и умножения, систематическое проведение содержательного и напряженного устного счета |
|||||
|
Общеучебные умения и навыки, элементы развития |
|||||||
|
Недостаточная техника чтения (в особенности – математических текстов, условий задач), большие проблемы в понимании текста учащимися из-за обедненного лексического запаса у части детей, неумение делить текст на смысловые час- |
сильное ухудшение
ситуации |
Постоянно предлагать учащимся задания на проверку знания и понимания смысла математических терминов, вести словарики терминов, читать вслух и анализировать условия задач, рекомендовать и родителям проводить такую работу с детьми при |
|||||
|
Ошибки в письменном делении многозначных чисел |
улучшение ситуации |
Регулярное повторение всех этапов алгоритма выполнения деления, систематическое включение в устную работу заданий на табличное умножение |
|||||
105 106
|
|
|
и деление, сложение и вычитание |
|
Ошибки в письменном умножении многозначных чисел |
ухудшение ситуации |
Регулярное повторение всех этапов алгоритма выполнения умножения, систематическое включение в устную работу заданий на табличное умножение и сложение |
|
Слабое знание правил порядка выполнения действий ( в т.ч. и в выражениях со скобками) |
сильное ухудшение ситуации |
После записи вычислительных примеров начинать с выделения отдельных «блоков», из которых он состоит, обращать внимание на «сильные» и «слабые» знаки арифметических действий, а затем расставлять номера действий |
|
Недостаточные умения решать текстовые задачи (даже и в одно-два действия) |
ухудшение ситуации |
Предлагать сначала представить себе ситуацию, о которой речь в задаче, изобразить ее на рисунке или схеме. При обсуждении решения задавать вопросы: как догадались, что первое (второе и т.д.) действие – именно такое? |
|
Недостаточное развитие графических умений |
стабильное положение
|
Регулярное выполнение чертежей как на бумаге в клетку (с подсчетом числа клеточек – например, начертить отрезок длиной 6 клеток, от выбранной точки отступить вниз на 4 клетки и т.п.), так и на нелинованной бумаге, построение фигур по командам |
|
Формальные представления об уравнении, его корне, способах проверки правильности решения уравнения |
стабильное положение
|
Большее внимание уделять первым этапам формирования понятия переменной, верного и неверного равенства, нахождению значения выражения с переменной |
|
Недостаточно грамотная математическая речь учащихся |
стабильное положение
|
Учителю чаще давать образцы чтения выражений, равенств, уравнений и неравенств, скло- |
|
|
|
нять числительные, тренировать школьников в верном чтении математических выражений, использовании названий натуральных чисел и дробей в косвенных падежах |
Список литературы
1. Нешков К.И. Некоторые вопросы преемственности при
обучении математике // Преемственность в обучении математике. – М.: Просвещение, 1978. С. 13–18.
2. Хинчин А.Я. Педагогические статьи: Вопросы преподава-
ния математики. Борьба с методическими штампами. М.: Изд.
АПНРСФСР. 1963. 208 с.
3. Аксенова М.В., Мендыгалиева А.К. «Ретроспектива про-
блемы реализации преемственности образования в отечественной и зарубежной педагогике» http://www.science-education.ru/128-22280
4. Чернышова О.В. «Математические проблемы
преемственности начальной и средней школы» http://festival.1september.ru/articles/610803/
5. Далингер В.А. «Проблемы преемственности начального и среднего звена системы школьного математического образования» http://www.rae.ru/meo/?article_id=187&op=show_article§ion=cont ent
6. Жохов В. «Преемственность в обучении математике между начальной школой и 5 классом» http://www.distedu.ru/ mirror/_fiz/ archive.1september.ru/mat/2000/no25_1.htm
7. Калиберова А.И. «Формирование у школьников умения
учиться» http://festival.1september.ru/articles/618070/
E.A. Osipova
Private institution High educational school "Potentsial", Moscow e-mail: [email protected]
PROBLEM OF CONTINUITY OF TRAINING OF SCHOOL
STUDENTS AT ELEMENTARY AND MAIN SCHOOL
Article is devoted to a complex actual problem of continuity of training of school students at elementary and main school. Questions on
107
which the emphasis is placed, mention the maintenance of a school course, ways of a statement of this contents, a form and methods of the organization of educational process, change of style of the relations between pupils and teachers and their influence on success of the subsequent training.
Key words: mathematics, continuity, school.
УДК 51-76
Охотникова Н.В.1, Шевцова Т.В.2 e-mail: [email protected], e-mail: [email protected]
1
Селиховская средняя общеобразовательная школа,
Курская область
2
Юго-Западный государственный университет, Курск
ИНТЕГРИРОВАННЫЕ ЗАНЯТИЯ ПО ЕСТЕСТВЕННОНАУЧНЫМ ДИСЦИПЛИНАМ:
МАТЕМАТИКА-БИОЛОГИЯ, МАТЕМАТИКА-ХИМИЯ
В статье изложены основные направления развития научной мысли в контексте синтеза отдельных естественнонаучных дисциплин и показаны целесообразность и возможности отражения указанных тенденций в учебном процессе.
Ключевые слова: интеграция наук, биоматематика, математическая химия, математическое моделирование, математическая
статистика, дифференциальные уравнения, числа Фибоначчи
В генезисе мировой научной мысли можно выделить несколько этапов: становление основных крупных видов знаний, их предметная дифференциация, затем интеграция областей из различных наук и, наконец, появление комплексных наук. В процессе дифференциации основополагающей науки по содержанию выделяются новые научные дисциплины. Далее в ходе развития они неизбежно сталкиваются с необходимостью обращения к другим наукам, к использованию их теоретической базы и практических методов. В результате появляются новые науки на стыке уже существующих.
108
Сейчас различные научные дисциплины не существуют независимо, а взаимодействуют и влияют на развитие друг друга.
К примеру, совокупность сведений о живой природе привело к рождению науки – биология, в которой выделились самостоятельные направления: ботаника, зоология, морфология, экология, физиология. Последующее развитие связано с привлечением знаний и методов, скажем, из химии, физики, географии, и соответствующим появлением смежных наук: биохимия, биофизика, биогеографии, а также более узких областей типа почвоведении, океанологии и т.д.
В рассматриваемой цепочке развития научной мысли особым звеном выступает математика. Она обеспечила многим наукам переход от описательных к экспериментальным, обогатила теоретическую базу биологии, химии и других дисциплин и наделила их широким арсеналом методов решения практических задач. В результате появились такие разделы, как математическая биология и математическая химия, считающиеся сегодня отдельными самостоятельными науками.
Математическая биология (биоматематика) представляет собой теорию математических моделей биологических явлений. В ней исследуются биологические проблемы средствами математики и информатики, а получаемым результатам дают биологическую интерпретацию. Создателем биоматематики считается ученый украинского происхождения Николай Рашевский (1899-1972), который начал свои исследования с рассмотрения процесса деления клеток с точки зрения физики и математики, а затем перешел к исследованию биологических систем с использованием теории множеств и математической логики.
Главным направлением химической математики выступает математическое моделирование гипотетически возможных химических процессов и исследование их зависимости от свойств атомов и структуры молекул.
К числу математических разделов, используемых в биологии и химии, можно отнести математическое моделирование, теорию дифференциальных уравнений, математическую статистику, теорию графов, векторную алгебру, топологию, теорию групп, фрактальную геометрию, математическую логику, комбинаторику, теорию бифуркаций, методы искусственного интеллекта. Приведем
109
некоторые примеры, являющиеся лишь малой частью разнообразия применения математического аппарата в химии и биологии.
Математические модели в абстрактной форме представляют биологическую систему или химический процесс. Созданы модели отдельных частей тела (например, сердца), разработаны модель климата и экосистемы, модель «хищник-жертва», клеточные автоматы; в химии популярны модель «реакция – диффузия», модель «молекулярный граф», модель «закон действующих масс», определяющая скорости химической реакций.
Компьютерная обработка моделей позволяет перебирать все возможные варианты развития событий и построить разнообразные прогнозы. Выделяются даже такие научные области, как хемоинформатика (химическая информатика) и биоинформатика, занимающиеся передачей, хранением и обработкой информации об особенностях химических элементов и химических реакций и свойствах биологических систем.
Для описания динамики биологических и химических процессов и явлений используются алгебраические и дифференциальные уравнения. Например, уравнение роста живых организмов: у(t)=уK-(уK-у0) ·e-kt ,
у(t) – размер объекта в зависимости от возраста t, уK – макси-
мальный размер, у0 – начальный размер, k – постоянная роста.
Получено дифференциальное уравнение, демонстрирующее зависимость скорости роста численности популяции у'(t) от численности y(t) в конкретный момент времени t: у'(t)=r·y(t).
В дальнейшем уравнение было уточнено и приобрело вид: у'(t+1)=r·y(t)·(1- y(t)).
Представление данных в виде специальных таблиц – матриц позволяет формализовать сведения и применять матричный аппарат для исследований. Например, с помощью матриц можно проанализировать химическую структуру молекулы. Трехмерное компьютерное моделирование биологических и химических процессов не может обойтись без применения матриц и операций над ними. Одно из самых актуальных научных направлений – изучение генома, записанного в ДНК клеток организма, использует матрицы, элементами которых являются вероятности, характеризующие возможности получения определенного результата. При изучении эво-
110
люции видов путем анализа цепочек ДНК применяются так называемые цепи Маркова – последовательности случайных событий, вероятность которых зависит от предыдущих результатов.
Тенденция синтеза знаний из разных областей должна находить отражение в образовании. В связи с этим актуальна идея интегрированных занятий по разным дисциплинам. На наш взгляд, она может быть реализована как собственно проведением отдельных мероприятий с привлечением разных преподавателейпредметников, так и периодическим обращением к возможностям одной дисциплины при проведении занятий по другой. Целесообразность проведения интегрированных занятий по естественнонаучным дисциплинам подтверждается достижением положительных результатов: расширение кругозора и формирование общей картины мира, развитие познавательного интереса, усиление мотивации к изучению как математики, так и биологии и химии.
Тематика подобных мероприятий может быть весьма разнообразной и соответствовать реальному применению математики в биологии и химии. Кроме того, уместными оказываются и фрагментарные обращения к математическому аппарату.
Для демонстрации практической значимости математики полезным оказывается формулировка некоторых задач с использованием биологических терминов.
Пример. Для нормальной жизни в промышленном городе на каждого жителя необходимо иметь 25 м2 зеленых насаждений. Какова должна быть площадь насаждений в городе Курск, если в нем проживает 431171 человек?
Огромные приложения в биологии имеет последовательность Фибоначчи. Ее встречаем при определении листорасположения, при выяснении места семян в корзинках сложноцветных и чешуй в шишках голосеменных, при подсчете колючек на стебле кактусов и т.д. Во всех отмеченных случаях спирали заворачиваются навстречу друг другу, число правых и левых спиралей всегда относится друг к другу как соседние числа Фибоначчи. По законам золотого сечения построены тела бабочек, стрекоз, ящериц, форма яиц птиц, костный лабиринт внутреннего уха. Двойная спираль молекулы ДНК почти полностью соответствует числам ряда Фибоначчи.
111
Изучаемые в старших классах вопросы генетики требуют обращение к математике как при освоении теоретического материала, так и при решении конкретных практических задач.
Указанные выше факты дают преподавателям огромный потенциал для проведения интегрированных занятий.
В школьном курсе химии имеют место разнообразные задачи, решение которых делает необходимым использование математических приемов, например, обращение к пропорциям и работа с процентными соотношениями. Мы призываем не только к выполнению вычислительных действий, а к осознанному составлению математических моделей, позволяющих как решать задачу по конкретным исходным данным, так и строить прогнозы при изменении начальных условий. Например, задачи на смеси, растворы и сплавы, как правило, сводятся к составлению модели:
w1·m1 + w2·m2 + … + wn·mn = w·(m1 + m1 + … + mn), где m1, m2 …, mn – массы смешиваемых веществ, w1, w2 …, wn –
их концентрации, w – концентрация получившегося вещества.
Заметим, что решение подобных задач оказывается полезным и в связи с тем, что они встречаются в обязательном и в едином государственных экзаменах по математике. Например, в открытом банке заданий по математике можно найти следующую задачу.
Задача. Имеется два сплава. 1-ый содержит 10% никеля, второй 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?
Если х – масса 1-го сплава, то математическая модель такова:
0,1·х + 0,3·(200-х) = 200·0,25.
Дальнейшие вычислительные действия позволяют определить массы исходных веществ и решить задачу.
В химии встречаются задачи, требующие не только составления уравнений и их систем, но и обращение к дифференциальному и интегральному исчислению. Химия работает с вопросами механизмов химических реакций, а скорость химической реакции есть не что иное, как производная концентрации продуктов по времени. Из этого получают законы, описывающие химические процессы.
Задача. Газовая смесь состоит из окиси азота NO и кислорода O2. Требуется найти концентрацию O2, при которой содержащаяся в смеси окись азота окисляется с наибольшей скоростью.
112
Реакция окисления окиси азота имеет вид: 2NО + O2 = 2NO2.
Установлено, что процесс окисления выражается формулой: v(с)= Kc2(100-с), где К – некоторая постоянная, с – концентрация (в процентах) NO, а (100-с) – концентрация O2. Найдем производную v'(с)= (K(100c2 – с3))'=K(200c-3c2). Стационарная точка соответствует v' = 0 и, следовательно, K(200c-3c2)=0, откуда с = 200/3 = 66,67 %. Так как в этой точке производная меняет знак с «+» на «-», то она и соответствует наибольшей скорости реакции.
Отметим, что при реализации межпредметной связи математики с биологией и химией, изучение одной дисциплины не подменяется изучением другой. Напротив, открываются возможности усовершенствования преподавания каждого из предметов.
Наверное, жизнь на Земле невозможно описать несколькими формулами и уравнениями, но разобраться с отдельными правилами – задача, посильная математике. На протяжении всего курса биологии и химии преподаватель имеет возможность обосновывать гармоничность окружающего мира и единство всех проявлений жизни и сделать это с математической точностью.
Список литературы
1. Комиссаров, Б.Д. Методологические проблемы школьного биологического образования / Б.Д. Комиссаров. М.: Просвещение, 1991. 160 с.
2. Мир математики: в 40 т. Т.28: Рафаэль Лаос-Бельтра. Математика жизни. Численные модели в биологии и экологии. М.: Де Агостини, 2014. 160 с.
3. Парахонский, А.П. Интеграция и дифференциация наук, их связь с образованием / А.П. Парахонский, Е.А. Венглинская // Успехи современного естествознания. 2009. № 9. С. 86-87.
Okhotnikova N.V.1, Shevtsova T.V.2
e-mail: [email protected], e-mail: [email protected]
Selihovskaja secondary school, Kursk region
Southwest State University, Kursk
INTEGRATED CLASSES IN NATURAL SCIENCES:
MATHEMATICS-BIOLOGY, MATHEMATICS-CHEMISTRY
113
The article describes the main directions of development of scientific thought in the context of the synthesis of different disciplines and the desirability and possibility of reflection of these trends in the educational process
Key words: integration of science, biomathematics, mathematical chemistry, mathematical modeling, mathematical statistics, differential equations, Fibonacci numbers.
УДК 51
Е.А. Панина, А.Ф. Пихлап e-mail: [email protected]
Юго-Западный государственный университет, Курск.
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ КОНСПЕКТИРОВАНИЯ
В данной статье рассмотрены основы конспектирования, зависимость его от условий и целей, психологические особенности конспекта.
Ключевые слова: конспект, мыслительная деятельность, психологическая особенность, информация, речевое сообщение.
Развитие науки и техники требует постоянного совершенствования и качества подготовки специалистов и повышения их квалификации. Неуклонное и быстрое овладение достижениями науки, техники, передовым опытом становится жизненной потребностью каждого специалиста. В высшей школе осуществляется поворот от массового обучения к усилению индивидуального подхода, развитию творческих способностей будущих специалистов, вследствие чего большое значение приобретает самостоятельная работа студентов при методической помощи и контроле со стороны преподавателя. В связи с этим за последнее десятилетие особенно остро встал вопрос об интенсификации процесса обучения в высшей школе. Педагогический коллектив высшей школы должен помочь студенту в усвоении и понимании новых методов их обучения, новых методов речевого общения.
114
Одним из таких вдов речевого общения, которое требует навыков самостоятельного творческого мышления, является конспектирование. Под конспектированием мы понимаем процесс мыслительной переработки и письменной фиксации читаемого или аудируемого текста; процесс, результатом которого является запись, позволяющая конспектирующему студенту немедленно или через некоторое время с необходимой полнотой восстановить полученную информацию.
С первых дней пребывания в высшей школе студенты сталкиваются с необходимостью конспектирования, поскольку в лекциях дается сводный материал, почерпнутый дается сводный материал, почерпнутый из разных источников, что при современном бурном развитии всех отраслей науки естественно и оправданно, и большая часть содержащейся в лекциях информации не может сразу запечатлеться в памяти студента.
Конспектирование является сложным и очень своеобразным процессом. В нем сочетаются аудирование или чтение (рецептивный или речевой деятельности) с письмом (продуктивный вид деятельности). Однако разные виды речевой деятельности при конспектировании сочетаются не механически. Фиксации полученной информации предшествует её специфическая обработка, которая заключается в свертывании текста. Конспектирующий не просто отбрасывает ненужную для него информацию и сокращает текст, а именно сворачивает его таким способом, чтобы и через достаточно длительный промежуток времени суметь вновь его развернуть без существенной утраты информации.
Студенты, не владеющие искусственным конспектированием, поступают по-разному: пытаются вести запись со стенографической точностью, составляют план вместо конспекта, выборочно записывают наиболее важную и трудно запоминаемую информацию.
Стремление к точному воспроизведению лекционного материала приводит к пропускам и в конечном счете к частичным, но невосполнимой утрате информации. Необходимо заметить, что стенографирование лекций студентами менее целесообразно. Чем конспектирование, т.к. стенографическая запись требует дополнительного времени для расшифровки. Мыслительные операции, сопровождающие процесс конспектирования позволяют студенту лучше усваивать материал уже в самом процессе знании . Экспери-
115
ментально доказано, что самостоятельно сформулированная фраза запоминается в семь раз быстрее, чем фраза записанная под диктовку.
Составление подробного плана вместо записи лекции также не приводит к положительным результатам. Чем больше времени проходит со дня такой записи, тем меньше информации восстанавливается.
Запись наиболее важных, с точки зрения студентов и трудно запоминаемых сведений приводит к разрушению логического построения материала. Информация, зафиксированная таким образом, вместе с информацией, которая хранится в памяти автора записи, не воссоздает целостной системы знаний.
Испытывая трудности при записи лекции, студенты иногда вообще отказываются от конспектирования и пользуются чужими конспектами, которые имеют репутацию образцовых. В таких случаях может возникнуть иллюзия, что пользование чужим конспектом затруднительно только из-за неразборчивости скорописи и сокращенного написания слов. В таких случаях конспект может служить полноценным пособием только самому конспектирующему.
Конспектирование лекций – наиболее трудный вид конспектирования ввиду ограниченности времен, в течение которого необходимо сделать запись.
Дефицит времени нельзя, тем не менее, считать единственной трудностью конспектирования. При подготовке курсовых работ, проектов, докладов и выступлений студенты сталкиваются с необходимостью знакомиться и конспектировать большое количество печатных источников, а работа по нескольким печатным текстам на одну тему еще более усложняет эту задачу, поскольку при конспектировании печатных текстов студенты встречаются с таким трудностями, как отсутствие быстрого чтения. Трудности конспектирования определяются специфическими условиями, в которых чаще всего протекает этот процесс.
Чаще всего в повседневной практике студентам приходится заниматься конспектированием лекций. Это процесс характеризуется рядом особенностей, которые связаны со специфическим временным соотношением рецептивного и продуктивного видов речевой деятельности со сложной комбинаторикой процессов переключения и распределения внимания.
116
Чтение лекции – это акт вербального общения и, следовательно, акт коммуникации. Обычно лекция подготовлена заранее и своей развернутостью приближается к письменной речи. В аудиторных условиях между лектором (источником информации) и конспектирующим(приёмником информации) существует взаимосвязь. Поэтому специфику условий и особенности конспектирования надо рассматривать в свете коммуникативной теории речи и теории информации.
Для успешного усвоения лекции лектору необходимо руководствоваться следующими положениями:
1. Темп речи лектора должен быть значительно ниже темпа речи, свойственного конспектирующему, если же темп речи лектора значительно выше речи конспектирующего нарушается полное усвоение содержания услышанного и в этой связи возникает быстрое утомление в результате перегрузки памяти.
2. Конспектирование возможно лишь в том случае, когда содержащаяся в лекции информация доступна, понимаю конспектирующих, для этого необходим тщательный отбор информации лектором и относительной однородности аудитории, т.е. конспектирующие имеют примерно одинаковый уровень знаний.
3. Слишком большая разница между уровнями лексикосинтаксической культуры лектора и конспектирующими может затруднить аудирование и конспектирование лекции.
Итак, конспект является результатом приема переработки и фиксации речевого сообщения, предназначенного для личного пользования. Особенности конспекта находятся в зависимости от условий и цели конспектирования.
Главной психологической особенностью конспекта можно считать особый характер его коммуникативности.
В любом конспекте зафиксирована предъявленная лектором информация, однако по отбору, переработке и способу запечатления информации конспект приобретает сугубо индивидуальный характер.
_____________
1. Кузнецов О.А., Коренев А.Н. Быстрое чтение: разработка модели и практика обучения. Вопросы психологии. М.: Высш.
Школа, 1976. №4. С.90-102.
117
2. Павлова В.П. Обучение конспектированию. М.: Русский язык, 1989. 96 с.
E.A. Panina, A.F. Pihlap e-mail: [email protected] Southwest State University, Kursk
THEORETICAL FOUNDATIONS OF NOTE-TAKING
This article describes the basics of note-taking, its dependence on the conditions and objectives, the psychological characteristics of the summary.
Key words: abstract, intellectual activity, psychological feature, information, voice message.
УДК 514 А.С. Сеитова e-mail: [email protected]
Жетысуский государственный университет имени
И. Жансугурова. Республика Казахстан
Научный руководитель: Г.О. Кожашева, канд. пед.наук, доц.
ПРИЛОЖЕНИЯ ТЕОРИИ ПОВЕРХНОСТЕЙ
Статья написана в соответствии с программой курса геометрии для математических факультетов университетов. В статье уделено большое внимание практической направленности. Изложение теории сопровождается примерами решения задач по теории поверхностей.
Ключевые слова: теория поверхностей, прикладные задачи.
Возникновение дифференциальной геометрии связано именами Л. Эйлера и Г. Монжа. В конце XVIII века Эйлер и Монж получили важнейшие факты теории поверхности. Монж написал свое первое сводное сочинение по теории поверхности
(«Приложение анализа к геометрии» 1795г.).
118
В начале XIX века К. Гаусс вложил свой вклад в развитие дифференциальной геометрии. В 1827 году была опубликована работа Гаусса «Общее исследование о кривых поверхностях», в которой ученый заложил основы теории поверхностей в ее нынешнем виде. С этого времени дифференциальная геометрия стала самостоятельной частью математики.
XXI век требует от современного человека нового подхода ко многим аспектам жизни, в том числе и инженерии и технологии применения.
Дифференциальная геометрия поверхностей – раздел математики, изучающий поверхности методами дефференциальной геометрии. При этом исследуемые поверхности подчинены условиям, связанным с возможностью применения методов дифференциального исчисления. Эти требоания сводятся к тому, что функции, задающие поверхность, прелдолагаются однократно, дважды, трижды, а в некоторых вопросах неограниченное число раз дифференцируемыми или даже аналитическими функциями.
Новизна исследования заключается в том, что, применяя в жизни современную инженерию, мы все чаще обращаемся к дифференциальной геометрии.
В данной работе были поставлены цели и задачи:
1. Исследовать теорию поверхностей
2. Формировать познавательную деятельность посредством внедрения теории поверхности дифференциальной геометрии на практике.
Объектом исследования данного проекта выступают приложения теории поверхностей.
Для изучения поверхностей необходима векторная функция
![]()
r u, двух скалярных аргументов u и υ.
Первоначальное представление о поверхности мы получаем, рассматривая поверхности твердых тел, наблюдая часть земной суши или мгновенное состояние поверхности моря и т.п.
Математически строгое определение поверхности основывается на понятиях топологии. При этом основным является
119
понятие простой поверхности, которую можно представить как кусок плоскости, подвергнутый непрерывным деформациям.
Концепция поверхности применяется в физике, инженерном деле, в математике, компьютерной графике, в разных технических областях при изучении физических объектов. Примеры применения теории поверхности на практике:
Пример 1. На поверхности сферы задан прямоугольный треугольник, сторонами которого являются дуги больших кругов сферы. Найти а) соотношение между сторонами треугольника; б) его площадь. Решение.
а) Возьмем уравнение сферы в виде
x Rcosucosv, y Rcosusinv, z Rsinu.
Расположим один из катетов на линии u 0, второй – на линии v , одну из вершин в точке B (u 0,v 0), вторую – в точке A (u ,v ). Тогда длины катетов равны соответственно
a R; b R. Для вычисления c надо найти длину дуги линии
AxBz0 (не поверхности сферы) между указанными точками.
Уравнение гипотенузы в криволинейны координатах
Acosusinv Bsinu 0. Так как она проходит через точку sin
u ,
v ,
то sinv ktg
u, где k ![]() .
.
tg
![]()
![]() c
s
R
1 k2
cosu2du 2 R arc sin(
1 k2
sin)
c
s
R
1 k2
cosu2du 2 R arc sin(
1 k2
sin)
0 1(1 k )sin u
R arc sin 1cos2cos2 ,
отсюда
![]() c a b cos
c a b cos ![]() coscos cos cos .
coscos cos cos .
R R R
120
f (v)
б) SR2cosududvR2dv cosudu,
D 0 0 sinv где
f (v)
arctg ![]() . k
. k
![]() 2 sinv 2
2 sinv 2
S
R sinarctg ![]() k dv
R
k dv
R
0
R2(arcsin 1 arcsin
![]() 1k2
1k2
Отсюда
a c
![]() sin S
sin2 k2 kcos sinsin
sin Rsin R .
sin S
sin2 k2 kcos sinsin
sin Rsin R .
R2 1 k2 1cos 1cos c
R
Пользуясь соотношением
tg
cosB ![]() ,
получим tg
,
получим tg
sin sinsin
sinB ![]() ,
cos(A B)
,
cos(A B)
![]() , sin 1cos
, sin 1cos
sinsin
![]() sin(A B ) .
sin(A B ) .
2 1cos
Сравнивая с предыдущим, находим
S R2(A
B
![]() ).
).
![]() 2 c a b 2
1 .
2 c a b 2
1 .
![]()
![]() Ответ.
cos coscos cos cos ,
S R
(A B
)
Ответ.
cos coscos cos cos ,
S R
(A B
)
R R R 2
Пример 2. Анализ аэродинамических качеств самолета базируется на обтекании потоком воздуха его поверхности.
121
Пример 3. Основные эксплуатационные свойства деталей машин зависят от точности их изготовления и качества поверхности.
Износ трущихся поверхностей, зарождение трещин усталости, коррозионное разрушение — это процессы, протекающие на поверхности деталей и в некотором прилегающем к поверхности слое. Под термином «поверхностный слой» понимается сама поверхность и ее некоторый подповерхностный слой, отличающийся от материала сердцевины детали.
Учение о качестве поверхности относится к числу важных достижений отечественной технологической науки, открывает новые возможности значительного повышения качества, надежности и долговечности деталей машин.
Под качеством поверхности понимают состояние поверхностного слоя детали.
Параметры, характеризующие качество поверхности:
1. Геометрические параметры;
2. Физико-механические свойства; 3. Структура поверхностного слоя.
Пример 4. Архитектура с древнейших времен была сопряжена с математикой. В основном это выражалось в использовании знаний в области геометрии. В начале XX века на фоне общего усиления роли науки в архитектурно - строительной отрасли взаимосвязь ее с миром математики эволюционирует. В частности активно исследуются свойства математических поверхностей. Особую популярность при обретают линейчатые поверхности в силу того, что поверхности этого класса обладают высокой прочностью. Их пространственная структура достаточно наглядна, а сооружения на их основе обладают относительной конструктивной простотой, что дает возможность архитекторам масштабно использовать этот класс поверхностей. Создание форм на основе аналитических поверхностей является сравнительно новым актуальным направлением в концептуальном архитектурном проектировании 2.
Из вышесказанного следует, что применение теории поверхностей на практике способствует развитию современной технологии, оказывая положительное влияние в обучение математике. Требуется дальнейшая научная и практическая проработка нового направления применительно к практике проектирования. Это направление в науке еще не достаточно изучено и требует дальней-
122
шего совершенствования. В XXI веке с внедрением новых технологий именно это направление найдет широкое применение.
___________________________
1. Сайт Allbest.ru «Теория поверхностей в задачах и примерах»
2. Горнева О.С. Математические методы в учебном архитектурном проектировании// « Архитектон», 2004. №12
A.S. Seitova e-mail: [email protected]
Of Zhetysu state university named after I. Zhansugurov
Scientific adviser: G. O. Kozhasheva, candidate of pedagogical sciences, associate professor
SUPPLEMENT OF THE THEORY OF SURFACES
The article is written in accordance with the program of the course of geometry for mathematical faculties of universities. The article is about great attention the practical orientation. Presentation of the theory is accompanied by examples of solving problems in the theory of surfaces.
Key words: the theory of surface, applied tasks.
123
УДК 378
Л.И.Студеникина, Д.Н. Тютюнов e-mail:[email protected]
Юго-Западный государственный университет, Курск
МЕЖДИСЦИПЛИНАРНЫЙ ПОДХОД В ИЗУЧЕНИИ
МАТЕМАТИЧЕСКИХ ДИСЦИПЛИН
Рассматривается междисциплинарный подход в обучении математике студентов младших курсов, как необходимый элемент образовательного процесса в плане подготовки к будущей профессиональной деятельности
Ключевые слова: математика, наука, математическая модель, задачи, студенты.
Одной из важнейшей функции математики, как фундаментальной науки, является создание теоретической научной базы знаний для успешного овладения дисциплинами профессионального цикла и формирование у студентов мышления, при котором осуществляется целостный подход к изучаемому предмету как к системе, состоящей из множества взаимосвязанных элементов.
Формирование такого мышления возможно на основе системного рассмотрения теоретического математического материала и использования междисциплинарного подхода, реализующего связь математики с другими учебными дисциплинами, необходимыми студентам в их будущей профессиональной деятельности. [1]
Математика изучается в первый и второй год обучения в бакалавриате, в течение этого периода студенты получают базовые знания. Затем, на 3, 4 курсах и в магистратуре есть специальные математические курсы, направленные на углубление математической подготовки, необходимой для применения математики непосредственно в сфере выбранной профессии. Например, студенты, будущие инженеры машиностроительных специальностей, достаточно глубоко изучают моделирование при
124
подготовке машиностроительного производства, моделирование процесса функционирования технических систем, математическую статистику в машиностроении и т. д.
В лабораторном практикуме «Математическое моделирование процессов в машиностроении» студенты работают не только с довольно стандартными расчетными формулами, но и решают задачи оптимизации режимов резания, в которых требуется поэтапно составить математическую модель, определить целевые функции и выбрать метод решения оптимизационной задачи. При выполнении работы «Моделирование процесса врезания инструмента одностороннего резания», приходится решать систему линейных уравнений. [2] Для успешного решения подобного рода задач необходимо в период обучения на первом и втором курсах дать студентам требуемые математические знания и обозначить задачи, с которыми им придется столкнуться на старших курсах.
Особое место в учебном процессе занимает математическая статистика. Она играет огромную роль в машиностроении, приборостроении. Во многих технологических процессах есть необходимость систематически контролировать состояние процесса, чтобы вмешиваться при отклонениях его от нормального режима и предотвратить тем самым потери от выпуска некачественной продукции. Для этого используются статистические методы контроля качества. Важной является задача статистической оценки показателей деятельности производственных предприятий и проведение прогнозного исследования. [3]
Для решения обозначенных проблем студенты должны хорошо владеть методом наименьших квадратов, уверенно использовать методы дисперсионного, регрессионного и корреляционного анализов. Сами методы изучаются на практических и лабораторных занятиях по математике на первом и втором курсах. На кафедре высшей математики разработан учебнометодический комплекс лабораторных работ для экономических и инженерных специальностей. Часть лабораторных работ имеют профессиональную направленность. Например, в лабораторной работе «Метод наименьших квадратов» индивидуальные задания выдаются в соответствии с направлением, по которому обучаются
125
студенты. В процессе ее выполнения студент вначале строит математическую модель своей задачи, выбирает метод решения, реализовывает выбранный метод решения на ЭВМ; анализирует результаты решения. Опыт показал, что такие профессионально направленные задания вызывают больший интерес у студентов, чем стандартно сформулированные задачи с «обезличенными данными». Появляется дополнительная мотивация при выполнении лабораторной работы. Как следствие, улучшается математическая подготовка.
Таким образом, междисциплинарный подход способствует становлению связей между математикой и дисциплинами профессионального цикла, повышает мотивацию студентов к активной учебно-познавательной деятельности.
Список литературы
1.http://www.dissercat.com/content/mezhdistsiplinarnyi-podkhod-vobuchenii-matematike-studentov-bakalavriata
2. Дерябин И.П., Козлов А.В. Математическое моделирование процессов в машиностроении: Учебное пособие по выполнению лабораторных работ. Челябинск: издательство ЮУрГУ, 2003. 27 с.
3. Барботько А.И., Гладышкин А.О. Математическая
статистика в машиностроении: учеб. пособие; Курск. гос. техн. унт. Курск, 2006. 320 с.
4. Студеникина Л.И., Тютюнов Д.Н. Лабораторные работы как эффективный инструмент подготовки студентов к решению профессиональных задач. Сборник научных статей IV
Международной научно-практической конференции, 2013. 214 с.
L.I. Studenikina, D.N. Tyutyunov e-mail:[email protected]
Southwest State University, Kursk,
INTERDISCIPLINARY APPROACH IN STUDYING
OF MATHEMATICAL DISCIPLINES
126
Interdisciplinary approach in training in mathematics of junior students, as a necessary element of educational process in respect of preparation for future professional activity is considered.
Key words: mathematics, science, mathematical model, tasks, students.
УДК 378:51
Т.В. Тихоненко, М.В. Задорожнюк e-mail:[email protected]
Гомельский государственный технический университет имени
П.О.Сухого, г. Гомель, Республика Беларусь
ОПЫТ ПРЕПОДАВАНИЯ МАТЕМАТИКИ
ПРОГРАММИСТАМ
В настоящей работе рассмотрены основные вопросы, связанные с проблемами преподавания математики студентампрограммистам, а также проведен анализ, позволяющие понять насколько знание математики влияет на профессиональный рост и востребованность будущего ИТ-специалиста.
Ключевые слова: образование, проблемы преподавания, математика, математическое мышление, информатика.
«Математику уже затем учить надо, что она ум в порядок приводит»
М. Ломоносов
В данной работе мы попытались разобраться, насколько нужна математика программисту и какие возникают проблемы при преподавании математики студентам-программистам в нашем вузе.
Первый из поставленных вопросов очень часто приходится слышать от студентов-программистов и их родителей. Первые задаются этим вопросом, когда у них возникают проблемы при решении задач в области математического анализа, алгебры и геометрии, статистики, теории вероятностей. Вторые – видя как их
127
дитя «мучается», решая и доказывая математические задачки, интересуются, так ли важна математика для будущего программиста.
Дать однозначно верный ответ на это вопрос нельзя. Проведя небольшой анализ, мы пришли к выводу, что для решения некоторых ИТ-задач нужно знать математику лучше, чем некоторые ученые, а для других – она совершенно не нужна. Например, если программист занимается инфраструктурными, инженерными задачами, то ему, скорее всего, понадобятся совсем другие умения. Так же в программировании есть задачи, в которых гуманитарное образование больше поможет, чем фундаментальное математическое. Это те области, где приходится больше работать с пользователями. Например, при разработке интерфейса, который должен быть удобен среднестатистическому пользователю, глубокое математическое образование будет только мешать, потому что интерфейс может получиться очень стройным и при этом совершенно неудобным.
Однако в программировании есть достаточно широкий класс задач, где глубокие математические знания играют большое значение. Для красочного понимания этого приводится простое сравнение. Есть люди, которые рисуют картины – их называют художники. Есть люди, которые красят заборы, – это маляры. Вот так же и с программистами: есть некоторый класс программистов, которые творят что-то высокотехнологичное, а есть те, что «красят заборы». В конечном итоге одних от других во многом отличает знание математики. Дальше выбор делает сам программист. Или он начинает заниматься математикой, тогда у него появляется шанс стать «художником». Или все время пользоваться готовыми алгоритмами и библиотеками, которые написали программисты более высокого класса. Математика нужна в системном программировании на нижнем уровне, в криптографии, в искусственном интеллекте и в других областях. Например, машинное обучение – это математическая дисциплина, использующая разделы математической статистики, численных методов оптимизации, теории вероятностей, дискретного анализа выделяющая знания из данных. Как говорит директор отделения компьютерных наук ШАДа и HR-директор Яндекса, доктор физико-математических наук, профессор Е.И. Бунина: «Кто имеет
128
дело с машинным обучением, должен знать математику, должен хорошо владеть алгоритмами, и для него очень важны знания статистики».
На наш взгляд, для подготовки высококвалифицированных ИТ-специалистов, закладывать знание математики обязательно. Понимание математики необходимо просто потому, что она выстраивает логику мышления (ведь не зря табличка с известным высказыванием М. Ломоносова висит почти в каждой школе в кабинете математики). У программиста развивается абстрактное мышление, он может лучше смотреть на задачу, разбивать ее на части, понимать пути решения, искать новые подходы к решению – это в любом программировании важно. Например, с оценкой сложности алгоритмов, использующей базовые знания математики, программисту приходится сталкиваться в любой ситуации – какую бы программу он ни писал.
Теперь перейдем к рассмотрению второго вопроса: проблемы при преподавании математики программистам в нашем ВУЗе.
Одна из первых проблем, с которой сталкивается студентпервокурсник – это различие требований, предъявляемых к нему при изучении математики в школе и в университете. Речь идет не о «больших» или «меньших» требованиях, а о принципиально разных подходах к оценке «достижений» студента.
Хотя школьная программа построена таким образом, чтобы за время обучения ученик получил некие фундаментальные математические знания, владение которыми поможет успешно справиться и с университетской программой, на деле школа большинством даже хороших учеников воспринимается как некий трамплин, который позволит успешно сдать централизованное тестирование и поступить в ВУЗ. Поэтому основное внимание школьники уделяют не овладению базовыми математическими понятиями и инструментами, не попыткам понять логику предмета, не умению строить строгие логические цепочки, доказывать и обосновывать утверждения, а приобретению навыков решения конкретных задач определенных типов. При изучении очередной темы первый вопрос, который волнует ученика, это не «как это можно использовать», а «будет ли эта тема в ЦТ», и, если не будет, то и изучать ее незачем. Безусловно, навыки решения задач весьма полезны и необходимы и, конечно, высокий балл на
129
централизованном тестировании значительно расширяет возможности для выбора ВУЗа и специальности. Но такой подход приводит к тому, что студенты даже такой популярной и востребованной ИТ-специальности как, например, «Информатика и технологии программирования» совершенно серьезно полагают, что программист – это человек, который пишет программы, используя языки программирования и стандартную библиотеку алгоритмов, а математика к его работе не имеет никакого отношения.
Все это формирует у большинства потенциальных студентов представление о математике как о науке, главной задачей которой является решение неких примеров и задач по определенным схемам, и мнение о том, что студенту достаточно отработать навыки решения нескольких классов типовых задач, чтобы утверждать, что он знает математику.
Однако уже на первом курсе вчерашние ученики оказываются в растерянности: при изучении университетского курса математики студент должен не только и не столько натренироваться в решении типовых задач, сколько ознакомиться с различными математическими теориями, понять их и уметь применить на практике, и, кроме того, на основе полученного ответа сделать некий вывод. Вполне естественно, что непривычные требования не вызывают особого энтузиазма: лекционные занятия большинством студентов воспринимаются как непонятный «довесок» к «главному» – практическим занятиям, на которых можно делать привычные действия – считать по формулам. При этом любые попытки придать математическим вычислениям реальный смысл вызывают сопротивление: студент легко вычислит производную, но далеко не каждый найдет мгновенную скорость в точке, при вычислении интеграла от неотрицательной функции получит в ответе, например, ноль, но будет абсолютно уверен, что все сделал правильно, т.к. в его сознании вычисление интеграла (практический навык) никак не связан с площадью (геометрический смысл определенного интеграла).
Часто студент бывает разочарован и своей оценкой на экзамене: умение решать типовые задачи в школе гарантировало, по крайней мере, не ниже восьми баллов. В ВУЗе же решение без каких-либо обоснований и объяснений, почему нужно делать
130
именно так и что из этого следует, оценивается гораздо ниже. Цель изучения математики в университете заключается не просто в выработке умений и навыков решения задач, а в формировании привычки аналитического и логического мышления. В конечном итоге, задача университета – подготовить специалиста, который сможет самостоятельно анализировать и решать поставленные перед ним задачи. Возможно, в будущей профессии, программистам, например, не пригодятся производные или матрицы, но если и пригодятся, то именно в прикладных задачах, предполагающих знание общей теории, а не в виде типового примера. Конечно, вряд ли современный инженер будет вручную строить графики функций, но умение собирать, анализировать и интерпретировать информацию ни для кого не будет лишним.
В заключение хочется отметить, что решать изложенные проблемы можно как с позиции школы, так и с позиции ВУЗа. Возможно, каких-то из описанных трудностей можно было бы избежать, если бы общеобразовательные кафедры, такие как кафедра высшей математики, физики и т.п., были больше «привязаны» к факультетам, и преподаватель, читая лекции, ссылался бы на приложения математики к решению задач характерных для данной специальности. Может быть, тогда математика стала бы для студентов менее абстрактной и более прикладной наукой.
T.V. Tihonenko, M.V. Zadorozhnyuk e-mail:[email protected]
Sukhoi State Technical University of Gomel, Gomel, Belarus
THE EXPERIENCE OF TEACHING MATHEMATICS
TO STUDENTS PROGRAMMERS
The basic issues related to the problems of teaching mathematics to students programmers and analysis, that allows us to understand how knowledge of mathematics affects on the professional growth and the demand in perspective IT-specialists, are considered in this paper.
Key words: education, problems of teaching, mathematics, mathematical way of thinking, computer science.
131
УДК 372.851
Шалимова А.В.1, Шевцова Т.В.2 e-mail: [email protected], e-mail: [email protected]
1
Лицей № 21, Курск
2
Юго-Западный государственный университет, Курск
ВАРИАТИВНОСТЬ ПРИЕМОВ РЕШЕНИЯ
ГЕОМЕТРИЧЕСКИХ ЗАДАЧ КАК СРЕДСТВО
ДОСТИЖЕНИЯ КАЧЕСТВА МАТЕМАТИЧЕСКОЙ
ПОДГОТОВКИ
В статье проанализирована проблема изучения стереометрии в школе и вузе, рассмотрены основные сложности, возникающие у учащихся при этом, и предложены способы повышения уровня математических знаний и умений.
Ключевые слова: стереометрия, планиметрия, пространственное мышление, координатный метод
Изучение стереометрии традиционно вызывает сложности у учащихся как в процессе формирования теоретических знаний, так и в ходе их применения к решению практических задач. Рассмотрим основные возникающие проблемы и предложим возможные пути их решения.
История методики преподавания математики знает подход, при котором изучение планиметрических и стереометрических фактов идет параллельно и оправдывается особенностями формирования пространственного воображения учащихся. Однако сегодня, курс стереометрии, как правило, является естественным продолжением курса планиметрии. Решение пространственных задач в ряде случаев сводится к рассмотрению линий и фигур некоторой плоскости. Как следствие, пробелы в знаниях по планиметрии не позволяют успешно освоить стереометрический материал. Кроме того, зачастую можно установить аналогию между теоретическими фактами, связанными с объектами на плоскости и объектами в пространстве. Таким образом, первым требованием успешного усвоения стереометрии выступает высокий уровень подготовки по пла-
132
ниметрии. Поэтому изучение геометрии в старших классах должно начинаться с серьезного повторения курса 7-9 классов.
Стереометрия отличается богатым теоретическим материалом. Соблюдение научной строгости изложения обязывает рассматривать основные аксиомы стереометрии и следствия из них, множество теорем, свойств, признаков, устанавливающих взаимное расположение объектов в пространстве. Не имея большого опыта работы с теоретическим материалом, учащиеся вначале испытывают сложности и, как следствие, не всегда в должной мере получают необходимые знания. Решение этой проблемы во многом связано с деятельностью учителя по контролю теоретических знаний. Проведение математических диктантов на проверку теоретических знаний, подбор заданий, направленных на уточнение материала оказываются весьма продуктивными .- 0июбубю
Следующей проблемой выступает изображение пространственных фигур на плоскости. В геометрии чертеж имеет первостепенное значение, однако здесь он оказывается лишь искаженным представлением рассматриваемых объектов. На первых порах уместно использование на уроках математики пространственных моделей, однако, в дальнейшем это может затормозить развитие пространственного мышления, к тому же само создание моделей становится затруднительным.
Большинство учащихся сталкиваются с проблемой плохо развитого пространственного мышления. Полезными в этой связи являются разнообразные задачи на выяснение взаимного расположения объектов.
Задача. (Рис. 1) Дан тетраэдр ABCD, F – середина BD, E – середина BC, P – середина EC. Используя рисунок, указать 1) плоскости, в которых лежат точки A, B, F; 2) плоскости, в которых лежат прямые AC, PE, AF; 3) тоски плоскости АВС, BCD; 4) взаимное расположение прямых AB и CA, CD и EF, FP и CD, AD и BC; 5) прямые, по которым пересекаются плоскости ABC и FED, ADC и ABF.
При доказательстве теоретических фактов и решении задач целесообразным является выполнение не однообразных чертежей (на доске и в тетради), а изображение нескольких вариантов. Это позволит увидеть фигуру с разных точек зрения, что будет способствовать выработке умениярешать стереометрические задачи.
|
133 Развитию пространственного воображения способствуют задачи на построение сечений тел. В ходе их решения приходится на- |
134 |
![]() ходить пересечение прямых
и плоскостей или доказывать их параллельность, что дает возможность углубить первичные
знания и умения по стереометрии. Кроме того, зачастую имеют место разные способы
решения, мы убеждены в том, что уместным оказывается уменьшение количества рассматриваемых
задач в пользу рассмотрения различных вариантов решения одной.
ходить пересечение прямых
и плоскостей или доказывать их параллельность, что дает возможность углубить первичные
знания и умения по стереометрии. Кроме того, зачастую имеют место разные способы
решения, мы убеждены в том, что уместным оказывается уменьшение количества рассматриваемых
задач в пользу рассмотрения различных вариантов решения одной.
Задача. Требуется построить сечение параллелепипеда ABCDA1B1C1D1 плоскостью MNK, если M – середина BB1, N лежит на AA1, так что AN = 1/3 AA1, K лежит на AD, так что AK = 1/3 AD.
B
Построение.
![]() 1
способ (Рис. 2) 1) Проведем MN и NK.
1
способ (Рис. 2) 1) Проведем MN и NK.
2)Найдем точку Т – точку пересечения прямых MN и АВ (построение ведется в плоскости АA1B1).
3)Найдем точку S – точку пересечения прямых TK и BC (построение ведется в плоскости АBC).
4)MNKS – искомое сечение.
Построение, конечно, сопровождается необходимым доказательством, обоснованием принадлежности плоскости сечения точек
T и S.
2 способ (Рис. 3)
1) Проводим MN и NK.
2) Строим точку S –середину ВС.
Тогда прямая MS параллельна прямой NK, так как AN = 1/3 AA1, AK = 1/3 AD и BM = 1/2 BB1, BS=1/2 BC, следовательно, лежит в плоскости сечения.
3) MNKS – искомое сечение.
Конечно, первый способ решения задачи является универсальным, второй основывался на том, что в задаче фигурировали пропорциональные отрезки.
A K D
Рис. 3
135
Методы решения задач по планиметрии и стереометрии в корне отличаются. В первом случае есть возможность работать с реальными построениями, чертеж полностью отвечает требованиям задачи и помогает найти решение. Во втором мы лишь описываем проводимые построения и мысленно выясняем расположение объектов. Именно поэтому так важно рассмотреть различные способы решения задач, даже в ущерб их количеству.
В вузе изучение планиметрии и стереометрии, как правило, сводится к рассмотрению аналитической геометрии на плоскости и в пространстве и к применению координатно-векторного метода решения задач. Возможности этого метода в небольшом объеме изучаются уже в школьном курсе математики и часто представляют собой альтернативу геометрическим приемам решения задач. Мы убеждены в важности формирования у учащихся представлений о единой основе методов и предлагаем иногда обращаться к каждому из них при решении задачи.
Таким образом, к основным проблемам, возникающим при изучении стереометрии, мы отнесли следующие: низкий уровень знаний и умений по планиметрии, не развитость пространственного мышления, необходимость изображения пространственных фигур на плоскости, большой объем сложного для восприятия теоретического материала. Без целенаправленной работой над их решением невозможно добиться высокого результата.
Список литературы
1. Геометрия. 10-11 классы: учеб. для общеобразоват. учреждений: базовый и профильный уровни / Л.С.Атанасян и др. М.:
Просвещение, 2012. 255 с.
2. Гусев В.А., Орлов В.В., Панчишкина В.А. Методика обучения геометрии. М.: Академия, 2004. 369 с.
3.Колягин Ю.М. и др. Методика преподавания математики в средней школе. Частные методики. Учеб. пособие для студентов физ.-мат. фак. пед. ин-тов. М.: Просвещение, 1977. 480 с.
4. Лурье М.В. Геометрия. Техника решения задач. Учеб. пособие. М.: Издательство УНЦ ДО, 2004. 240 с.
Shalimova A.V.1, Shevtsova T.V.2
136
e-mail: [email protected], e-mail: [email protected]
1
Lycee № 21, Kursk
2
Southwest State University, Kursk
VARIABILITY OF METHODS OF SOLVING GEOMETRIC
PROBLEMS AS THE MEANS OF ACHIEVING QUALITY
MATHEMATIC TRAINING
The problem of studying stereometry in schools and universities is analyzed in the article, the basic difficulties of it are considered, and the ways to increase of level of mathematical knowledge and abilities are offered
Key words: stereometry, planimetry, spatial thinking, coordinate method
УДК 372.851
Шевцова Т.В.
e-mail: [email protected]
Юго-Западный государственный университет, Курск
АУДИТОРНАЯ И САМОСТОЯТЕЛЬНАЯ РАБОТА
УЧАЩИХСЯ ПРИ ИЗУЧЕНИИ КООРДИНАТНОГО МЕТОДА
В ШКОЛЕ И ВУЗЕ
В статье рассмотрены проблемы решения геометрических задач на основе координатного метода и эффективной организации аудиторной и самостоятельной работы учащихся при этом.
Ключевые слова: координатный метод, прямоугольная декартова система координат, правильные многогранники.
Сегодня в школьном курсе математики координаты и векторы выступают объектами специального изучения. Знакомство с числовой осью и прямоугольной системой координат на плоскости происходит уже в 5 и 6 классах. Здесь рассматривается понятие координаты точки и фактически устанавливается биективное отображе-
137
ние множества чисел (сначала рациональных, позднее действительных) и пар чисел на множество точек прямой и плоскости соответственно. В 7 и 8 классах в неявном виде осуществляется работа с координатным методом, когда вводятся уравнения различных линий на плоскости: прямой, параболы, гиперболы, затем окружности. Далее в 9 классе объясняется сама суть координатного метода и его возможностей. Изучается понятие вектора, рассматриваются операции над векторами, скалярное произведение векторов на плоскости, вводятся координаты вектора и координаты точки как координаты ее радиус-вектора и, главное, показываются приложения метода к доказательству теорем и решению задач. Стоит заметить, что главным приложением выступает нахождение угла между векторами и, как следствие, угла между прямыми. В 11 классе вводится пространственная система координат и уделяется внимание заданию точек и векторов в пространстве, при этом новые возможности координатного метода обычно не рассматриваются. Как правило, решаются задачи только на нахождение угла между векторами или прямыми и на вычисления расстояние между двумя точками. Уравнения плоскости и прямой в пространстве, если и рассматриваются, то только в качестве дополнительного материала. Следовательно, почти не затрагиваются и вопросы поиска расстояния между различными геометрическими объектами или угла между ними.
Нехватка времени на рассмотрение подобных вопросов отчасти объясняется тем, что оно в большом объеме тратится на установление координат точек пространственных фигур. Так, в каждой геометрической задаче на эту тему описывается способ введения системы координат и устанавливаются координаты всех вершин рассматриваемой фигуры.
В вузе имеет место обратная ситуация. После подробного изучения векторной алгебры и рассмотрения скалярного, векторного и смешанного произведения векторов, открывается возможность освоить приложения координатного метода, а именно, нахождение расстояния между точкой и плоскостью, прямой и плоскостью, параллельными плоскостями и т.д., установление градусных мер углов между двумя прямыми, прямой и плоскостью и двумя плоскостями, вычисление площадей граней объемов тел. При этом, как правило, студенты оперируют с уже введенной системой координат
138
и с заданными координатами точек, а работа по оптимальному подбору системы координат и установлению координат точек не ведется.
С целью экономии учебного времени мы предлагаем сначала заняться заданием вершин часто встречающихся в пространстве тел, а затем пользоваться готовыми моделями для решения задач. Поскольку способов задания существует множество, то на этом этапе есть возможность организации самостоятельной индивидуальной работы учащихся. Уместным оказывается предлагать строить разные модели и соответственно получать разные задания точек фигур в пространстве.
Ниже приведены возможные способы задания некоторых многогранников, часто встречающихся в геометрических задачах.
1. Прямоугольный параллелепипед (в частности правильная четырехугольная призма и куб).
Длины ребер a, b, c
A(a,0,0), B(0,0,0), C(0,b,0),
![]() D(a,b,0), A1(a,0,c),
B1(0,0,c), C1(0,b,c),
D1(a,b,c) Для правильной четырехугольной
призмы длины ребер a, а, c
D(a,b,0), A1(a,0,c),
B1(0,0,c), C1(0,b,c),
D1(a,b,c) Для правильной четырехугольной
призмы длины ребер a, а, c
A(a,0,0), B(0,0,0), C(0,а,0),
D(a,а,0), A1(a,0,c), B1(0,0,c),
C1(0,а,c), D1(a,а,c) Для куба длина любого ребра а
A(a,0,0), B(0,0,0), C(0,а,0),
D(a,а,0), A1(a,0,а), B1(0,0,а),
C1(0,а,а), D1(a,а,а)
2. Правильная треугольная призма
139
![]() Длина ребра основания
a, длина бокового ребра h
Длина ребра основания
a, длина бокового ребра h
![]() A(0,0,0),
B0,а,0,
С
32а,а2,0,
A(0,0,0),
B0,а,0,
С
32а,а2,0,
A (0,0,h), B10,а,h,С1 23а,а2,h
Длина ребра основания a, длина бо-
![]() 3а а
3а а
B 2 ,2,0,
,0, D(0,2а,0),
![]() 3а
а
3а
а
,0, F 2 ,2,0, A1(0,0,h),
3а 3а
![]() B1
2 ,2,h,
С1
2 , 2 ,h,
B1
2 ,2,h,
С1
2 , 2 ,h,
3а 3а
D1(0,2а,h), Е1 2 , 2 ,h,
![]() 3а а
3а а
F1 2 ,2,h
4. Правильная четырехугольная пирамида
140
![]()
![]()
![]()
![]()
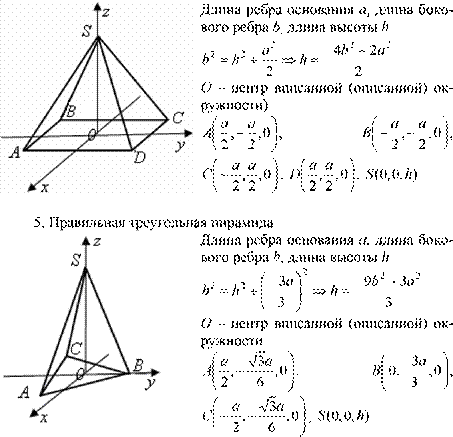
6. Правильная шестиугольная пирамида
Длина ребра основания a, длина боко-
![]() вого ребра b, длина высоты
h b2
h2
a2
h
b2
a2
вого ребра b, длина высоты
h b2
h2
a2
h
b2
a2
O – центр вписанной (описанной) окружности
![]() 3а а
3а а
A(0, a,0), B 2 , 2,0,
![]() 3а а
3а а
С 2 , 2,0, D(0,а,0),
141
![]()
![]()
![]() 3а а 3а а
3а а 3а а
Е 2 , 2,0, F 2 , 2,0, S(0,0,h)
Наверное, найдутся преподаватели, возражающие против описанного подхода, ведь выбор системы координат влияет на то, громоздкими или простыми окажутся вычисления. Однако мы убеждены, что наличие готовой модели полезным оказывается и в этом случае, ведь оно позволяет заранее “прикинуть” возможный результат, а, значит, и сделать вывод: оставить имеющуюся модель или построить новую.
Таким образом, не смотря на то, что в школьном и вузовском курсах математики уделяется внимание координатному методу, учащиеся, на наш взгляд, имеют не много возможностей полного его освоения, начиная от введения прямоугольной декартовой системы координат и заканчивая поиском конкретной величины. Предложенный метод использования готовых моделей для правильных многогранников позволяет сэкономить время и рассмотреть приложения координатного метода в большем объеме.
Список литературы
1. Ильин В.А., Позняк Э.Г. Аналитическая геометрия: учебник для вузов. Изд-во: ФИЗМАТЛИТ, 2009. 223 с.
2. Геометрия. 7-9 классы: учеб. для общеобразоват. учреждений: базовый и профильный уровни / Л.С.Атанасян и др. М.: Просвещение, 2008. 384 с.
3. Геометрия. 10-11 классы: учеб. для общеобразоват. учреждений: базовый и профильный уровни / Л.С.Атанасян и др. М.:
Просвещение, 2012. 255 с.
142
4. Столяр А.А. Педагогика математики: учеб. Пособие.
Минск: Высшая школа, 1986. 414 с.
Shevtsova T. V.
e-mail: [email protected]
Southwest State University, Kursk
CLASSROOM AND INDEPENDENT WORK OF STUDENTS
IN STUDY OF COORDINATE METHOD IN SCHOOL AND
UNIVERSITY
The article considers the problem of solving geometric tasks on the basis of the coordinate method and effective organisation of the classroom and independent work of students.
Keywords: coordinate method, rectangular Cartesian coordinate system, reciprocal polyhedrons.
УДК 51-72
С.В. Шеставина, О.А. Бредихина е-mail: [email protected]
Юго-Западный государственный университет, Курск
ОСОБЕННОСТИ ПОСТРОЕНИЯ РАЗВИТЫХ,
МАТЕМАТИЗИРОВАННЫХ ТЕОРИЙ В СОВРЕМЕННОЙ
НАУКЕ
В данной работе рассматривается связь математческой гипотезы с опытом. Математическая гипотеза чаще всего неявно формирует неадекватную интерпретацию создаваемого аппарата. Поэтому опытом проверяются не уравнения сами по себе, а система: уравнения плюс интерпретация.
Ключевые слова: гипотеза, интерпретация, уравнения.
С развитием науки меняется стратегия теоретического поиска.
В частности, в современной физике теория создается иными путя-
143
ми, чем в классической. Построение современных физических теорий осуществляется методом математической гипотезы. В отличие от классических образцов, в современной физике построение теории начинается с формирования ее математического аппарата, а адекватная теоретическая схема, обеспечивающая его интерпретацию, создается уже после построения этого аппарата. Новый метод выдвигает ряд специфических проблем, связанных с процессом формирования математических гипотез и процедурами их обоснования.
Первый аспект этих проблем связан с поиском исходных оснований для выдвижения гипотезы. В классической физике основную роль в процессе выдвижения гипотезы играла картина мира. По мере формирования развитых теорий она получала опытное обоснование не только через непосредственное взаимодействие с экспериментом, но и косвенно, через аккумуляцию экспериментальных фактов в теории. И когда физические картины мира представали в форме развитых и обоснованных опытом построений, они задавали такое видение исследуемой реальности, которое вводилось коррелятивно определенному типу экспериментальноизмерительной деятельности. Эта деятельность всегда была основана на определенных допущениях, в которых неявно выражались как особенности исследуемого объекта, так и предельно обобщенная схема деятельности, посредством которой осваивается объект.
Во-вторых, постулировалось, что пространство и время не зависят от состояния движения материальных тел (идея абсолютного пространства и времени). Такая концепция основывалась на идеализирующем допущении, что при измерениях, посредством которых выявляются пространственно-временные характеристики тел, свойства часов и линеек (жестких стержней) физической лаборатории не меняются от присутствия самих тел (масс) и не зависят от относительного движения лаборатории (системы отсчета). В современной физике приняты более сложные схемы измерения. Например, в квантовой механике элиминируется первое требование ньютоновской схемы, а в теории относительности — второе. В связи с этим вводятся и более сложные предметы научных теорий.
При столкновении с новым типом объектов, структура которых не учтена в сложившейся картине мира, познание меняло эту картину. В классической физике такие изменения осуществлялись в
144
форме введения новых онтологических представлений. Однако последние не сопровождались анализом абстрактной схемы измерения, которая составляет операциональную основу вводимых онтологических структур. Поэтому каждая новая картина физической реальности проходила длительное обоснование опытом и конкретными теориями, прежде чем получала статус картины мира. Современная физика дала образцы иного пути построения знаний. Она строит картину физической реальности, эксплицируя схему измерения, в рамках которой будут описываться новые объекты. Эта экспликация осуществляется в форме выдвижения принципов, фиксирующих особенности метода исследования объектов (принцип относительности, принцип дополнительности).
Сама картина на первых порах может не иметь законченной формы, но вместе с принципами, фиксирующими «операциональную сторону» видения реальности, она определяет поиск математических гипотез. Новая стратегия теоретического поиска сместила акценты и в философской регуляции процесса научного открытия.
В ходе математической экстраполяции исследователь создает новый аппарат путем перестройки некоторых уже известных уравнений. Физические величины, входящие в такие уравнения, переносятся в новый аппарат, где получают новые связи, а значит, и новые определения. Соответственно этому заимствуются из уже сложившихся областей знания абстрактные объекты, признаки которых были представлены физическими величинами. Абстрактные объекты включаются в новые отношения, благодаря чему наделяются новыми признаками. Из этих объектов создается гипотетическая модель, которая неявно вводится вместе с новым математическим аппаратом в качестве его интерпретации.
Такая модель, как правило, содержит неконструктивные элементы, а это может привести к противоречиям в теории и к рассогласованию с опытом даже перспективных математических аппаратов.
Таким образом, специфика современных исследований состоит не в том, что математический аппарат сначала вводится без интерпретации (неинтерпретированный аппарат есть исчисление, математический формализм, который принадлежит математике, но не является аппаратом физики). Специфика заключается в том, что математическая гипотеза чаще всего неявно формирует неадекват-
145
ную интерпретацию создаваемого аппарата, а это значительно усложняет процедуру эмпирической проверки выдвинутой гипотезы. Сопоставление следствий из уравнений с опытом всегда предполагает интерпретацию величин, которые фигурируют в уравнениях. Поэтому опытом проверяются не уравнения сами по себе, а система: уравнения плюс интерпретация. И если последняя неадекватна, то опыт может выбраковывать вместе с интерпретацией весьма продуктивные математические структуры, соответствующие особенностям исследуемых объектов.
Чтобы обосновать математическую гипотезу опытом, недостаточно просто сравнивать следствия из уравнений с опытными данными. Необходимо каждый раз эксплицировать гипотетические модели, которые были введены на стадии математической экстраполяции, отделяя их от уравнений, обосновывать эти модели конструктивно, вновь сверять с созданным математическим формализмом и только после этого проверять следствия из уравнений опытом. Длинная серия математических гипотез порождает опасность накопления в теории неконструктивных элементов и утраты эмпирического смысла величин, фигурирующих в уравнениях. Поэтому в современной физике на определенном этапе развития теории становятся необходимыми промежуточные интерпретации, обеспечивающие операциональный контроль за создаваемой теоретической конструкцией. В системе таких промежуточных интерпретаций как раз и создается конструктивно обоснованная теоретическая схема, обеспечивающая адекватную семантику аппарата и его связь с опытом.
_____________________________________________________
1. Кохановский В.П. Философия науки в вопросах и ответах / Ростов н/Д: Феникс, 2006. 352с.
2. Степин В.С. История и философия науки / М.: Академический Проект; Трикста, 2012. 423с.
S.V. Shestavina, O.A. Bredihina е-mail: [email protected]
Southwest State University, Kursk
146
FEATURES OF CONSTRUCTION ADVANCED,
MATHEMATICAL OF THE THEORIES IN A MODERN
SCIENCE
In the given job the communication mathematical of a hypothesis with experience is considered. Аучное изданиеThe mathematical hypothesis more often implicitly forms inadequate interpretation of the created device. Therefore experience checks not the equations in themselves, and system: the equations plus interpretation.
Key words: hypothesis, interpretation, equation.
147
Алфавитный указатель
Агеева Н.В. 6 Мокеева О.А. 79,85
|
Андриянова Т.В. 11 Басенко Н.В. 17 Башилова Е.А. 75 Бредихина О.А. 142 Великович Л.Л. 21 Волкова С.Н. 32 Герасимова В.В. 32 Гиоргадзе М.Г. 36 Должикова Л.А. 40 Дыбленко С.А. 17 Есенкова Г.А. 46 Есенкова Е.С. 46 Жумаев Ж.Н. 55 Жураев Д.А. 55 Жураева С.А. 61 Задорожнюк М.В. 126 Зарубина Н.К. 65 Иноземцева Е.И. 101 Костенко Н.А. 32 Крыжевич Л.С. 69 Мелентьев Д.А. 75 Меренкова Т.В. 36 |
Мокеева С.А. 79,85 Моргунова Е. Ю. 91 Моргунова Н. А. 91 Нурматова Н.Ш. 61 Осипова Е.А. 96 Охотникова Н.В. 107 Панина Е.А. 113 Пашкова М.И. 32 Пихлап А.Ф. 113 Рудюк С.В. 11 Ряднов А.В. 36 Сеитова А.С. 117 Сивак Е.Е. 32 Скрипкина Е.В. 17 Студеникина Л.И. 123 Тихоненко Т.В. 126 Тютюнов Д.Н. 123 Фильчакова К.А. 75 Шалимова А.В. 131 Шевцова Т.В. 107,131,136 Шеставина С.В. 142 |
148
НАУЧНОЕ ИЗДАНИЕ
АКТУАЛЬНЫЕ ПРОБЛЕМЫ
И ПЕРСПЕКТИВЫ
ПРЕПОДАВАНИЯ МАТЕМАТИКИ
Редактор Есипова В.А.
Компьютерная верстка и макет Есипова В.А.
Подписано в печать 29.09.2014 г.
Формат60x84 1/16, Бумага офсетная
Уч.-изд. л. 8,8 Усл. печ. л. 5,3 Тираж 100 экз. Заказ №277
Юго-Западный государственный университет
г.Курск, ул. 50-лет Октября, д.94
Отпечатано в типографии
Закрытое акционерное общество"Университетская книга" 305018, г. Курск, ул. Монтажников, д.12
ИНН4632047762 ОГРН1044637037829 дата регистрации 23.11.2004 г. Телефон +7-910-730-82-83
© ООО «Знанио»
С вами с 2009 года.
![]()

