Статья "Испытание на правдоподобие"

                                                                                                             Попова О.В

МБОУ СОШ №95

Воронеж

OVPOPOVA118@mail.ru

Испытание на правдоподобие

И специалисту-математику, и школьнику приходится встречаться с математическими предложениями, в истинности которых он сомневается. Иногда требуется доказать или опровергнуть ка­кое-либо утверждение или из нескольких предложенных ответов  к задаче выбрать единственный правильный.

Если доказательство утверждения упирается в громоздкие вык­ладки, то часто бывает полезно не начинать с попыток доказательства, а постараться отдать себе отчет, насколько данная гипотеза правдоподобна, не приводит ли она к явно ошибочным или сомнительным выводам»

Существуют некоторые простые общие приёмы, которые позволяют обнаружить ошибочный ответ к той или иной задаче, прове­рить, не содержит ли предложенная задача ошибочного утверждения и т.п.

Наиболее простые приёмы для достижения этой цели таковы:

проверка на частных случаях (с построением контрпримеров), про­верка по размерности.

В качестве примеров рассмотрим следующие задачи.

Задача 1.

В древнем Египте  для вычисления площади  четырехугольника, у которого длины последовательных сторон равны , , , , пользовались формулой:

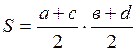
Справедлива ли эта формула для всех четырехугольников? Для ответа на этот вопрос в качестве частного случая здесь можно рассмотреть шарнирный квадрат со стороной, равной 1м и площадью 1м². Из этого квадрата путем сжатия можно получить ромб со стороной 1м, площадь которого будет меньше площади квадрата, а данная формула дает один и тот же результат. Значит, это ошибка.

Задача 2.

Будет ли справедлива для площади четырехугольника формула, сходная с формулой Герона:

?

Если стороны измерены, например, в метрах, то под корнем будет стоять величина размерностью м⁵, поэтому формула не верна. Эту формулу можно проверить и на предельном случае. Если а₄→ 0, то четырехугольник вырождается в треугольник, и для него верна формула Герона, а данная формула имеет вид:

Наличие любого большого числа разнообразных подтверждающих примеров еще не может служить доказательством правильности математического утверждения, но указание на один опровергающий пример («контрпример») полностью доказывает, что утверждение ошибочно. Такова сила «контрпримера».

Задача 3.

Ученику А представляется очевидным, что прямоугольник (рис. 1), описанный около правильного треугольника, имеет вдвое большую площадь, чем сам треугольник. Ученик В полагает, что это утверждение ошибочно. Кто прав?

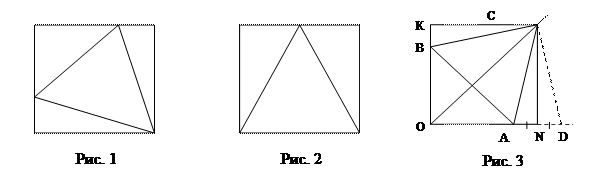
 Для выяснения истины ученики обратились к тому частному случаю, когда одна сторона треугольника целиком лежит на стороне прямоугольника (рис. 2). В этом случае гипотеза ученика А подтверждается. Однако это не значит, что она верна. Ученик В предлагает обратиться к другому частному случаю, когда диагональ описанного прямоугольника ONCK расположена на биссектрисе угла правильного треугольника АВС (рис. 3).

Положим . На продолжении отрезка ON отложим отрезок , тогда угол ACD = 30⁰, АВ = 

S_∆ ABC =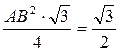

S_∆ AОВ + (S_∆ ANC+ S_∆ ВKC) = 0,5+ S_∆ AСD = 0,5+0,5=1

Отсюда ясно, что S_∆ AВС ≠ 0,5 S_ОNCK. Мы получили контрпример, опровергающий гипотезу ученика А.

Задача 4.

Ученик А убежден, что прямая, проходящая через центр тяжести любого четырехугольника, делит этот четырехугольник на две равновеликие части.

Проверка показала, что это утверждение верно для квадрата, прямоугольника, ромба, параллелограмма. Требуется либо доказать гипотезу ученика А, либо ее опровергнуть.

В случаях, рассмотренных учеником А, центр тяжести четырехугольника является одновременно и центром симметрии. Поэтому хорошим испытанием на правдоподобие будет рассмотрение какого-либо четырехугольника, не имеющего центра симметрии, например, трапеции.

Выберем такую трапецию, центр тяжести которой было бы не трудно найти (рис. 4)

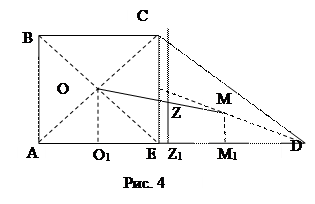Трапеция АBСD составлена из квадрата АВСЕ со стороной а и равновеликого с ним прямоугольного треугольника CED, ED = 2a.

Пусть О, М, Z - соответственно центры тяжести квадрата, треугольника и трапеции, О₁, М₁, Z₁ – проекции этих точек на прямую AD. Тогда Z середина отрезка ОМ, и легко подсчитать, что

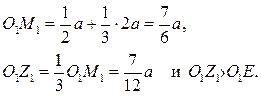
Следовательно, точка  Z₁ лежит между Е и D, так что прямая Z₁Z не делит трапецию на две равновеликие фигуры. Гипотеза ученика А ошибочна.

Скачано с www.znanio.ru