МБОУ СОШ№95

Проект

Дисциплина: математика

Тема: «Введение вспомогательных неизвестных как алгебраический прием для

    решения нестандартных геометрических задач»

Выполнили: Мозговенко Ирина и Болдырева Екатерина

Проверила:  Попова Ольга Валерьевна

Город Воронеж

2014 год

Введение вспомогательных неизвестных как алгебраический прием для решения нестандартных геометрических задач.

Умение решать задачи является одним из самых важных показателя уровня математического развития  и общей математической культуры каждого человека. Это умение зависит не от числа решенных задач, а от того, насколько четко сформулирован у человека общий подход к поиску плана решения задачи. Одним из самых популярных методов решения является алгебраический метод. Применение данного метода часто строится на введение вспомогательных неизвестных.

Если при решении задачи трудно выразить искомую величину через данные величины, то к числу искомых величин бывает целесообразно присоединить вспомогательные неизвестные, которые в ходе решения управлений (или систем) иногда удается исключить. В таких случаях вспомогательное неизвестное выступает в роли опорного элемента.

Рассмотрим решение следующих задач.

Задача №1.

Зная длины a, b, c и d последовательных сторон вписанного в окружность четырехугольника ABCD (AB=a, BC=b, CD=c, AD=d) вычислить длину его диагонали АС.

Решение:

1)  Из ∆АВС выразим АС через а, b и вспомогательное неизвестное:

АС²=a²+b²+2∙a∙b∙cos B;

2) Выразим АС из ∆ACD через d, c и вспомогательное   неизвестное соs D:

AC²=c²+d²-2∙c∙d∙cos D (1);

3) Т.к. в выпуклом четырехугольнике сумма противоположных углов равна 180°, то D=180°- B,

cos D=-cos B;

4) Тогда АС²= c²+d²+2∙с∙d∙cos B;

откуда cos B=

5) Подставим полученное выражение для вспомогательного неизвестного в равенство (1):

AC²=a²+b²-2ab*;

Тогда имеем:

АС²∙2∙с∙d=2∙c∙d∙a²+2∙c∙d∙b²-2∙a∙b∙AC²+2∙a∙b∙c²+2∙a∙b∙d²;

АС²∙2∙с∙d+ 2∙a∙b∙AC²= 2∙c∙d∙a²+2∙c∙d∙b²+2∙a∙b∙c²+2∙a∙b∙d²;

2∙AC²(c∙d+a∙b)=2(c∙d∙a²+c∙d∙b²+a∙b∙c²+a∙b∙d²);

AC²(c∙d+a∙b)=c∙d∙a²+c∙d∙b²+a∙b∙c²+a∙b∙d²;

Ответ: AC=

Задача №2.

В равнобедренной трапеции с острым углом α при основании окружность, построенная на боковой стороне как на диаметре, касается другой боковой стороны. В каком отношении она делит большее основание трапеции?

Решение:

1) Введем вспомогательное неизвестное:

OD=x

Пусть окружность пересекает большее основание трапеции в точке Е.

Тогда СED=90°, т. к. он опирается на диаметр.

Из ∆СED найдем DE:

сosα=;

cosα=

DE=2x*cosα.

2) Соединим точку Е с центром окружности и опустим перпендикуляр ОМ и EN на сторону АВ.

Рассмотрим ∆ODE.

Данные треугольник является равнобедренным =>

OED= ODE=α

Значит BAD= CDE=α

  Поэтому OE||AB

Отсюда NE=MO=x

И из ∆ANE получим, что AE=

Искомое отношение найдено;

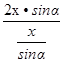==2cosα ∙sinα =sin2α

Ответ:=sinα

Задача №3.

Биссектрисы AD и CF треугольника АВС пересекают стороны ВС и АВ в точках D и F соответственно. Найти длину FD, если АС=6, AF=2, CD=3.

Решение :

1)Из ∆FBD по теореме косинусов имеем:

  FD²=FB²+BD²-2∙FB∙BD∙cosB

В этом уравнении три неизвестных: FB, BD и cos B

Следовательно, надо искать три уравнения для их                   отыскания.

Введем вспомогательные неизвестные

Пусть FB=x, BD=y. Тогда используя свойство биссектрисы треугольника, получим:

=                     6x=2y+6                    6x-2y=6

                  3x+6=6y                    3x-6y=6      

Решая систему, получим:

х=

у= 
Итак, FB=, BD= и АВ=, ВС=. Для определения косинуса угла В воспользуемся уравнением:

АС²=АВ²+ВС²-2∙АВ∙ВС∙сos B, т.е.

36=  +  -2∙∙∙cos B

∙cos B=

Итак, cos B=0, следовательно B=90°.

Из ∆FBD: FD==.

Ответ: FD=

Задача №4.

В треугольнике АВС биссектриса угла В делит сторону АС на отрезки AD=15 и DC=24 и образует с этой стороной угол 60°. Определите АВ и ВС.

Решение:

1)Введем вспомогательные неизвестные:

Пусть BD=а, АВ=х, ВС=у.

2)По свойству биссектрисы треугольника:

== (1)

3)По теореме косинусов имеем:

В ∆DAB: х²=а²+225-2∙15∙а∙;

х²=а²+225-15∙а (2);

В ∆DВС: у²=а²+576-2∙34∙а∙cos120°;

у²=а²+576+24∙а;

Исключим из этих уравнений а, для чего выразим х через у и подставим это выражение в равенство (2)

х=, тогда

= а²+225-15*а;

у²= и следовательно:

=а²+576+24∙а

Решая данное уравнение, получим, что а=40

Тогда х==35;

У==56.

Ответ: АВ=35, ВС=56.

Данный метод выделения вспомогательных неизвестных может широко применять для решения любых нестандартных задач различной сложности.

Овладение данным методом способствует:

-развитию математических способностей учеников;

-рассмотрению их математического кругозора;

-развитию познавательной активности и интереса к предмету в целом.

Данный метод повышает уровень общей математической культуры учащегося и способствует их развитию как личности в целом.