Бесконечная периодическая дробь

Пример

Представим дробь \(\frac{15}{22}\) в виде десятичной дроби. Для этого выполним деление «столбиком»:

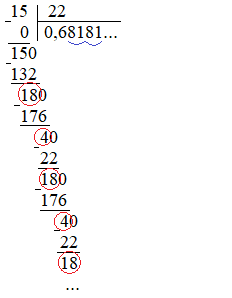
При делении образуются повторяющиеся ненулевые остатки. Поэтому деление
никогда не закончится, и конечная дробь не получится.

Начиная со второй цифры в дробной части повторяется число \(81\).

Поэтому \(\frac{15}{22}=0,6881818181 \ldots =0,6(81)\).

Получили бесконечную десятичную периодическую дробь.

Определение

Повторяющуюся группу цифр после запятой называют периодом дроби.

\(\frac{15}{22}=0,6\underline{(81)}\) - период дроби

Любое рациональное число можно записать в виде конечной десятичной дроби или в виде бесконечной десятичной периодической дроби.