Адаптированная образовательная программа для ребёнка с ограниченными возможностями здоровья по математике 7 класс ( вариант 4.1

1. ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Программа коррекционной работы по предмету математика,  предназначена для  коррекции предметных  навыков и умений детей  с  ОВЗ , с учетом  особенностей  их  психофизического  и  речевого  развития,  индивидуальных возможностей,  обеспечивающая  коррекцию  нарушений  развития  и  социальную адаптациюи оказание помощи детям этой категории в освоении ООП. Данная  программа предназначается обучающимся с нарушением зрения для  6  класса , обучение которых требуются особые педагогические условия, специальное систематическое целенаправленное коррекционное воздействие.

Коррекционная программа разработана в соответствии с требованиями   Федерального  государственного образовательного  стандарта  начального общего  образования  обучающихся  с  ограниченными  возможностями  здоровья.  Приказ  Минобрнауки России от 22  ноября 2022 г. № 1025 (в части требованиям к предметным результатам);  Федеральным государственным стандартом ООО, индивидуальным учебным планом учащегося с ЗПР .

Общая характеристика детей с ЗПР:

У детей с ЗПР в соматическом состоянии наблюдаются частые признаки задержки физического развития (недоразвитие мускулатуры, недостаточность мышечного и сосудистого тонуса, задержка роста), запаздывает формирование ходьбы, речи, навыков опрятности, этапов игровой деятельности.

У этих детей отмечаются особенности эмоционально-волевой сферы (её незрелость) и стойкие нарушения в познавательной деятельности.

Эмоционально - волевая незрелость представлена органическим инфантилизмом. У детей с ЗПР отсутствует типичная для здорового ребенка живость и яркость эмоций, характерны слабая воля и слабая заинтересованность в оценке их деятельности.

Игра отличается бедностью воображения и творчества, монотонностью, однообразием. У этих детей низкая работоспособность в результате повышенной истощаемости.

В познавательной деятельности наблюдаются: слабая память, неустойчивость внимания, медлительность психических процессов и их пониженная переключаемость. Для ребенка с ЗПР необходим более длительный период для приёма и переработки зрительных, слуховых и прочих впечатлений.

Для детей с ЗПР характерны ограниченный (гораздо беднее, чем у нормально развивающихся детей того же возраста) запас общих сведений об окружающем, недостаточно сформированные пространственные и временные представления, бедный словарный запас, несформированность навыков интеллектуальной деятельности.

Незрелость функционального состояния ЦНС служит одной из причин того, что дети с ЗПР не готовы к школьному обучению к 7 годам. У них к этому времени, как правило, не сформированы основные мыслительные операции, они не умеют ориентироваться в заданиях, не планируют свою деятельность. Такой ребенок с трудом овладевает навыками чтения и письма, часто смешивает буквы, сходные по начертанию, испытывает трудности при самостоятельном написании текста.

В условиях массовой школы дети с ЗПР попадают в категорию стабильно неуспевающих учеников, что ещё больше травмирует их психику и вызывает негативное отношение к обучению.

Общая характеристика детей с нарушением зрения:

 Обучающиеся с пониженным зрением (или с пограничным зрением между слабовидением и нормой), – это лица с остротой зрения от 0,5 (50 %) до 0,8 (80 %) на лучше видящем глазу с коррекцией. Основная специфика образовательного процесса инвалидов по зрению определяется особенностями реализации информационного обмена в условиях отсутствия (или значительного ограничения) визуального восприятия.

 В условиях зрительного дефекта усиливается психоэмоциональное напряжение, обостряется восприятие индивидом трудных жизненных ситуаций, осложняется выбор адекватных средств их преодоления, возникают состояние внутреннего психического конфликта, социальная дезадаптация, поведенческие нарушения и др.

 К числу специфических жизненных трудностей лиц с нарушениями зрения относятся:

– трудности в пространственной ориентировке (неумение пользоваться самостоятельными приемами ходьбы без зрения, психологические барьеры, препятствующие использованию трости и др.);

– трудности в общественной интеграции: высокая социальная неудовлетворенность, проблемы в общении с нормально видящими (формирование негативных коммуникативных установок и комплексов);

 – трудности в быту и самообслуживании

– несформированность элементарных бытовых умений и навыков, что наиболее характерно для слепорожденных, воспитывающихся в условиях гиперопеки, а также для лиц, потерявших зрение и адаптирующихся к измененным в результате этого условиям жизни;

  Глубина и характер поражений зрительного анализатора сказываются на развитии всей сенсорной системы, определяют ведущий путь познания окружающего мира, точность и полноту восприятия его образов. Врождённые и приобретённые нарушения зрения относятся к первичным соматическим дефектам. Эти аномалии вызывают вторичные функциональные отклонения (сужение поля зрения, сужение остроты зрения и т. д.), которые отрицательно сказываются на развитии ряда психических процессов: ощущении, восприятии, представлении и т. д. То есть, вторичные дефекты представляют собой цепь отклонений, где один функциональный дефект влечёт за собой другой, что приводит к нарушениям психических процессов. Поэтому между соматическим дефектом и аномалиями в развитии психики имеются сложные структурные и функциональные связи. Компенсаторное приспособление при слепоте не может быть достаточно полным, восстанавливающим нормальную жизнедеятельность человека без вмешательства извне. Слепой, без специально организованного обучения не способен овладеть самостоятельно направленной деятельностью, ввиду отсутствия или неполного, а иногда и искаженного представления о предметах окружающей действительности и возможных манипуляциях с ними.

 Нарушения зрения неоднозначно влияют на отдельные структурные компоненты личности, их компенсация рассматривается, как процесс перестройки психики и адаптации к новым условиям жизни. В основе механизма компенсации лежит приспособление организма, регулируемое ЦНС. Оно заключается в восстановлении или замещении нарушенных или утраченных функций организма независимо от того, где находится повреждение. Чем тяжелее дефект, тем большее количество систем организма включается в процесс компенсации. То есть, от тяжести дефекта зависит степень сложности механизмов компенсаторных явлений. Выпадение или нарушение зрительных функций при слепоте приводит к невозможности или затруднённости зрительного отражения мира. В результате из сферы ощущений и восприятия выпадают сигналы, информирующие человека о важных свойствах предметов и явлений.

 Компенсация пробелов в чувственном опыте обучающихся с нарушениями зрения возможна только при активном включении сохранных органов чувств, существенная роль, в деятельности которых принадлежит вниманию. Сокращение количества внешних воздействий, обусловленное полным или частичным выпадением зрительных ощущений и восприятия, препятствует развитию внимания, сокращая круг объектов, которые при восприятии вызывают непосредственный интерес. Это отрицательно сказывается на объёме, устойчивости, концентрации и других свойствах внимания обучающихся. В тоже время, однообразие слуховых раздражителей быстро утомляет слепого и ведёт к рассеиванию внимания. Хотя слепота и вносит некоторые специфические особенности в развитие и проявление внимания, но в целом внимание слепых подчиняется тем же закономерностям, что и у нормально видящих, и может достигать такого же уровня развития (Л. С. Выготский). Это обусловлено тем, что внимание формируется в деятельности и зависит от приобретённых волевых, эмоциональных и интеллектуальных свойств личности, от активности человека.

 На основе словесных объяснений, подкрепляемых доступными для слепых чувственными данными, лица с глубокими нарушениями зрения получают представления о многих недоступных для их восприятия предметах и явлениях действительности. Компенсаторная функция речи выступает во всех видах психической деятельности слепых студентов: в процессе восприятия (слово направляет и уточняет его), при формировании представлений и образов воображения, в ходе усвоения понятий и т. д. Огромное значение имеет речь для формирования личности слепого в целом. С помощью речи слепые контактируют с окружающими людьми, ориентируются в обществе. Недостатки произношения ограничивают круг общения лиц с патологией зрения, что тормозит формирование ряда качеств личности или ведёт к появлению отрицательных свойств (замкнутость, аутизм, негативизм и др.). Речь слепых при правильном формирующем воздействии со стороны родителей и педагогов развивается до нормального уровня и служит мощным средством компенсации, существенно расширяя возможности слепых во всех видах деятельности. Для компенсации зрительной депривации большое значение имеет взаимодействие ощущений.

  В результате под влиянием одной анализаторной системы повышается чувствительность другой. Утраченные зрительные функции замещаются большей частью деятельностью тактильного и кинестетического анализаторов. Это касается только слепых обучающихся. У слабовидящих ведущим видом ощущений остаётся зрение. Выпадение большого числа значимых объектов, их деталей и признаков из сферы восприятия препятствуют образованию общих представлений, в которых отражаются наиболее существенные свойства и признаки предметов и явлений.

 Мыслительная деятельность слепых и слабовидящих подчиняется в своём развитии тем же закономерностям, что и мышление нормально видящих. И хотя сокращение чувственного опыта вносит определённую специфику в этот психический процесс, замедляя интеллектуальное развитие и изменяя содержание мышления, оно не может принципиально изменить его сущности. При этом важная роль в компенсации зрительной депривации принадлежит «воссоздающему воображению». При его помощи слепые на основе словесных описаний и имеющихся зрительных, осязательных, слуховых и других образов формируют образы объектов, недоступных для непосредственного отражения. Ослепшие, на основе сохранившихся зрительных представлений могут создавать новые яркие образы воображения, а наличие остаточного зрения расширяет возможности в этом виде психической деятельности. Сам факт отсутствия зрения для слепых обучающихся не является фактором психологическим, они не чувствуют себя «погружёнными во мрак».

 Психологическим фактором слепота становится только тогда, когда они вступают в общение с нормально видящими людьми. Нарушение социальных контактов приводит к отклонениям в формировании личности слепого и может вызвать появление негативных характерологических особенностей. Таких как, изменения в динамике потребностей, связанные с затруднением их удовлетворения; сужение круга интересов, обусловленное ограничениями в сфере чувственного отражения; редуцированность способностей к видам деятельности, требующим визуального контроля; отсутствие или резкая ограниченность внешнего проявления внутренних состояний.

 В условиях слабовидения имеет место обедненность чувственного опыта, обусловленная не только снижением функций зрения и различными клиническими проявлениями, но и недостаточным развитием зрительного восприятия и психомоторных образований. У слабовидящих имеет место снижение двигательной активности и своеобразие физического развития (нарушение координации, точности, объема движений, нарушение сочетания движений глаз, головы, тела, рук и др.), в том числе трудности формирования двигательных навыков. При слабовидении имеет место своеобразие становления и протекания познавательных процессов, проявляющееся: в снижении скорости и точности зрительного восприятия, замедленности становления зрительного образа, сокращении и ослаблении ряда свойств зрительного восприятия (объема, целостности, константности, обобщенности, избирательности и др.); снижении полноты, целостности образов, широты круга отображаемых предметов и явлений; возникновении трудностей в реализации мыслительных операций, в развитии основных свойств внимания.

  Кроме того, слабовидящим характерны затруднения в овладении пространственными представлениями, в процессе микро- и макроориентировки, в словесном обозначении пространственных отношений; сложности в формировании представлений о форме, величине, пространственном местоположении предметов; ограничения возможности дистантного восприятия; низкий уровень развития обзорных возможностей; замедленный темп зрительного анализа. Слабовидящим свойственно своеобразие речевого развития (некоторое снижение динамики в развитии и накоплении языковых средств и выразительных движений, слабая связь речи с предметным содержанием, особенности формирования речевых навыков, недостаточный запас слов, обозначающих признаки предметов и пространственные отношения, трудности вербализации зрительных впечатлений и др.);наличие определенных трудностей в овладении языковыми (фонематический состав, словарный запас, грамматический строй) и неязыковыми (мимика, пантомимика, интонация) средствами общения, осуществлении коммуникативной деятельности (трудности восприятия, интерпретации продуцирования средств общения).

  Слабовидящим свойственны трудности, связанные с качеством выполняемых действий, автоматизацией навыков, осуществлением зрительного контроля за выполняемыми действиями, в том числе, связанными с будущей профессиональной деятельностью. Для слабовидящих характерно снижение уровня развития мотивационный сферы, регуляторных (самоконтроль, самооценка, воля) и рефлексивных образований. У части слабовидящих возможно формирование следующих негативных качеств личности: недостаточная самостоятельность, безынициативность, иждивенчество. У части обучающихся данной группы слабовидение сочетается с другими поражениями (заболеваниями) организма, что снижает их общую выносливость, психоэмоциональное состояние, двигательную активность, обусловливая особенности их психофизического развития. Таким образом, на формирование основных свойств личности обучающихся нарушения зрения влияют лишь косвенно, ведущая роль принадлежит социальным факторам (ограничение деятельности, негативный опыт общения с нормально видящими и т. п.).

Цель и задачи программы коррекционной работы

Цель:восполнение пробелов предшествующего развития;  коррекция дефекта;  подготовка ребенка к усвоению программного материала; создание специальных условий для освоения образовательных программ и социальной адаптации ребенка с тяжелыми нарушениями речи.

Задачи:

1. обеспечение системного подхода к созданию условий для развития ребенка, оказание комплексной помощи в освоении основной образовательной программы начального общего образования;

2. развитие познавательной активности, активизация интеллектуальной деятельности путем формирования умственных операций;

3. развитие речи, обогащения и систематизация словаря, развитие устной диалогической и монологической речи, составлению сюжетных и описательных рассказов;

4. коррекции индивидуальных недостатков развития ребенка, отклонений в его психическом, речевом и интеллектуальном развитии;

5. восполнение пробелов предшествующего развития, расширение кругозора, дальнейшее накопление представлений и знаний о предметах и явлениях ближайшего окружения ребенка;

6. выявление в содержании предметных областей универсальных учебных действий и определение условий их формирования в образовательном процессе и жизненно важных ситуациях;

7. формирование способности к саморазвитию и самосовершенствованию путем сознательного и активного присвоения нового социального опыта

Особенности программы:

·         Программа коррекционной работы позволяет наиболее успешно применять индивидуальный подход к каждому школьнику с учётом его способностей, более полно удовлетворять познавательные и жизненные интересы учащихся. В отличие от классных занятий, на внеклассных учащиеся мало пишут и много говорят.

·         Материал урока отбирается в зависимости от имеющихся нарушений. При планировании и проведении занятий особое внимание следует уделять предметно-практической деятельности.

·         Содержание индивидуальных занятий не допускает «натаскивания», формального механического подхода, должно быть максимально направлено развитие ученика. На занятиях необходимо использовать различные виды практической деятельности. Действия с реальными предметами, использованием наглядно-графических схем и т. п.

·         Создают возможность для широкой подготовки учащихся к выполнению различного типа задач: формирования пространственных представлений, умения сравнивать, обобщать предметы и явления, анализировать слова и предложения различной структуры; осмысления художественных текстов; развития навыков планирования собственной деятельности, контроля и словесного отчёта.

·         При работе с каждым типом упражнений, заданий нужно добиваться полного понимания и безошибочного выполнения, только после этого следует переходить к другому типу заданий. Желательно часть занятий проводить в игровой форме. Этим будет поддерживаться постоянный интерес к занятиям.

·         При проведении игр и упражнений следует исключить ситуацию неудач. Реакция на ошибки должна быть формой помощи.

·         Коррекционно-развивающие занятия должны обеспечить не только усвоение определенных знаний, умений и навыков, но также формирование приемов умственной деятельности.

·         Немаловажной задачей является выработка положительной мотивации к учению.

·         Индивидуальные коррекционные занятия учитель проводит по мере выявления у учащихся индивидуальных проблем в развитии, отставания в обучении. Индивидуальная помощь оказывается ученикам, испытывающим особые затруднения в обучении.

·         Периодически на индивидуальные занятия привлекаются дети, не усвоившие материал вследствие пропусков из-за болезни либо из-за «нерабочих» состояний (чрезмерной возбудимости или заторможенности) во время уроков

Формы проведения занятий

·         практические занятия с элементами игр и игровых элементов, дидактических и раздаточных материалов, ребусов, кроссвордов, головоломок.

·         самостоятельная работа (индивидуальная и групповая) .

Основные методы и технологии

·         технология разноуровневого обучения;

·         развивающее обучение;

·         технология обучения в сотрудничестве;

·         коммуникативная технология.

Выбор технологий и методик обусловлен необходимостью дифференциации и индивидуализации обучения в целях развития универсальных учебных действий и личностных качеств школьника

1.      Общие сведения об обучающемся

Трудности в изучении математики

-проблемы пространственной ориентировки, неразличение, неправильное называние геометрических фигур, форм окружающего;

-смешение математических понятий (периметр и площадь, частное и разность и т.п.);

-неспособность установить зависимость между величинами (часть- целое; скорость-время-длина пути при равномерном прямолинейном движении; цена-количество стоимость и др.), решить текстовую задачу в 1-2 действия;

-неумение пользоваться математической терминологией;

-неумение применить алгоритм (способ, прием) выполнения арифметического действия;

-неумение использовать свойства арифметических действий при выполнении вычислений с рациональными числами;

-проблемы в понимании математических отношений (больше/меньше, выше/ниже, дороже/дешевле; «больше/меньше на...», «больше/меньше в ...», «на сколько (во сколько раз) больше/меньше» и др.).

Общая характеристика общеучебных трудностей обучении:

-неумение включиться в учебную работу; неспособность самостоятельно начать выполнение задания;

-неготовность выполнять задание без пошаговой инструкции и помощи;

-непонимание, неумение выполнить многокомпонентное задание (состоящее из нескольких простых);

-недостаточная осознанность в усвоении и применении алгоритмов (правил);

-неумение пользоваться полученными знаниями-умениями при решении стандартных учебных и практических задач;

-неспособность учесть все условия и этапы решения задания в ходе его выполнения (неполное выполнение задания);

-смешение (подмена) алгоритмов, понятий; нарушение последовательности шагов алгоритма при его выполнении;

-подмена задания (логически и алгоритмически более простым);

-неспособность контролировать ход (процесс) и результат выполнения задания;

-неумение понять и объяснить причину своей ошибки, исправить ее;

-неумение применить знания в нестандартной ситуации;

-неумение решить учебную задачу с использованием «другого» приема (способа), сравнить решения по степени рациональности.

Особые образовательные потребности:

- обогащение чувственного опыта;

- развитие познавательной деятельности;

- развитие зрительного восприятия и сохранных анализаторов;

- обогащение и коррекция предметных и пространственных представлений;

- развитие познавательно и общей активности;

- повышение коммуникативной активности и компетентности;

- физическое развитие, повышение двигательной активности;

- формирование умений и навыков зрительной ориентировки в микро и макропространстве.

  Индивидуально ориентированные коррекционные мероприятия, обеспечивающие удовлетворение особых образовательных потребностей слабовидящих школьников в соответствии ФГОС, включают:

 - коррекцию и развитие дефицитарных функций (сенсорных, моторных, психических);

- развитие умений и навыков пространственной ориентировки, социально-бытовой ориентировки, коммуникативной деятельности, осязания и мелкой моторики;

- обучение активному использованию освоенных компенсаторных способов, умений и навыков, восстановленных и скорректированных зрительных функций в разных видах учебной деятельности;

- развитие навыков самостоятельной работы, развитие познавательной активности и познавательных интересов, формирование эмоционально-волевой сферы и положительных качеств личности.

  Имея ввиду особые образовательные потребности детей с нарушением зрения (потребность в ранней диагностике и начале коррекционно-развивающей работы, индивидуальном и дифференцированном подходе, непрерывности коррекционного воздействия, изменении содержания образования, путей его изучения (методов, средств, форм), а также пространственно-временной организации среды обучения) и их специфические потребности существует определенная характеристика информационного и материально-технического обеспечения ФГОС с позиции обеспечения наиболее комфортных условий получения образования и коррекционно-развивающей помощи. 

В основе обучения математики лежит овладение учащимися следующими видами компетенций: предметной, коммуникативной, организационной и общекультурной. В соответствии с этими видами компетенций выделены основные содержательно-целевые направления (линии) развития учащихся средствами предмета математика.

Предметная компетенция. Здесь под предметной компетенцией понимается осведомленность школьников о системе основных математических представлений и овладение ими основными предметными умениями. Формируются следующие образующие эту компетенцию представления: о математическом языке как средстве выражения математических законов, закономерностей и т.д.; о математическом моделировании как одном из важных методов познания мира. Формируются следующие образующие эту компетенцию умения: создавать простейшие математические модели, работать с ними и интерпретировать полученные результаты; приобретать и систематизировать знания о способах решения математических задач, а также применять эти знания и умения для решения многих жизненных задач.

Коммуникативная компетенция. Здесь под коммуникативной компетенцией понимается сформированность умения ясно и четко излагать свои мысли, строить аргументированные рассуждения, вести диалог, воспринимая точку зрения собеседника и в то же время подвергая ее критическому анализу. Формируются следующие образующие эту компетенцию умения: извлекать информацию из разного рода источников, преобразовывая ее при необходимости в другие формы (тексты, таблицы, схемы и т.д.).

Организационная компетенция. Здесь под организационной компетенцией понимается сформированность умения самостоятельно находить и присваивать необходимые учащимся новые знания. Формируются следующие образующие эту компетенцию умения: самостоятельно ставить учебную задачу (цель), разбивать ее на составные части, на которых будет основываться процесс ее решения, анализировать результат действия, выявлять допущенные ошибки и неточности, исправлять их и представлять полученный результат в форме, легко доступной для восприятия других людей.

Общекультурная компетенция. Здесь под общекультурной компетенцией понимается осведомленность школьников о математике как элементе общечеловеческой культуры, ее месте в системе других наук, а также ее роли в развитии представлений человечества о целостной картине мира. Формируются следующие образующие эту компетенцию представления: об уровне развития математики на разных исторических этапах; о высокой практической значимости математики с точки зрения создания и развития материальной культуры человечества, а также о важной роли математики с точки зрения формировании таких значимых черт личности, как независимость и критичность мышления, воля и настойчивость в достижении цели и др.

Воспитательный потенциал предмета "Математика" реализуется через:

-побуждение обучающихся соблюдать на уроке общепринятые нормы поведения, правила общения со старшими (педагогическими работниками) и сверстниками (обучающимися), принципы учебной дисциплины и самоорганизации. Методы и приемы: обсуждение правил общения со старшими (учителями) и сверстниками(школьниками), принципы учебной дисциплины и самоорганизации;

-привлечение внимания обучающихся к ценностному аспекту изучаемых на уроках предметов, явлений, событий через: обращение внимания на нравственные аспекты научных открытий, которые изучаются в данный момент на уроке; на представителей ученых, связанных с изучаемыми в данный момент темами, на тот вклад, который они внесли в развитие нашей страны и мира, на достойные подражания примеры их жизни, на мотивы их поступков. Методы и приемы: организация работы с получаемой на уроке социально - значимой информацией, инициирование ее обсуждения, высказывания обучающимися своего мнения, выработки своего отношения;

-использование воспитательных возможностей содержания учебного предмета для формирования у обучающихся российских традиционных духовно-нравственных и социокультурных ценностей. Методы и приемы: демонстрация детям примера ответственного, гражданского поведения, проявления человеколюбия и добросердечности, через подбор соответствующих текстов для чтения, задач для решения, проблемных ситуаций для обсуждения в классе);

-включение в урок игровых процедур, которые помогают поддержать мотивацию обучающихся к получению знаний, налаживанию позитивных межличностных отношений в классе, помогают установлению доброжелательной атмосферы во время урока;

-применение на уроке интерактивных форм работы, стимулирующих познавательную мотивацию обучающихся.

-применение групповой работы или работы в парах, которые способствуют развитию навыков командной работы и взаимодействию с другими обучающимися.

-выбор и использование на уроках методов, методик, технологий, оказывающих воспитательное воздействие на личность в соответствии с воспитательным идеалом, целью и задачами воспитания;

-инициирование и поддержка исследовательской деятельности школьников в форме включения в урок различных исследовательских заданий и задач, что дает возможность обучающимся приобрести навыки самостоятельного решения теоретической проблемы, генерирования и оформления собственных гипотез, уважительного отношения к чужим идеям, публичного выступления, аргументирования и отстаивания своей точки зрения. Методы и приемы: реализация индивидуальных и групповых исследовательских проектов.

-установление уважительных, доверительных, неформальных отношений между учителем и учениками, создание на уроках эмоционально-комфортной среды;

-организация шефства мотивированных и эрудированных учащихся над их неуспевающими одноклассниками, дающего школьникам социально значимый опыт сотрудничества и взаимной помощи. Методы и приемы: наставничество.

Сроки реализации программы: программа разработана для учащихся 7 класса общеобразовательной школы. Рассчитана на 2025-2026  учебный год.

Система оценки достижений учащихся.

Промежуточная аттестация учебного курса осуществляется через математические диктанты, самостоятельные работы, контрольные работы по разделам учебного материала, тесты.

Предлагаются учащимся разноуровневые тесты, т.е. список заданий делится на две части – базовый уровень(обязательный), повышенный и высокий уровень (необязательный). Обязательный уровень обеспечивает базовые знания для любого ученика. Необязательная часть рассчитана на более глубокие знания темы. Цель: способствовать развитию устойчивого умения и знания согласно желаниям и возможностям учащихся.Задания для устного и письменного опроса учащихся состоят из теоретических вопросов и задач.

Итоговая аттестация учебного курса: происходит по итогам написания тематических контрольных работ

Методы контроля:

ежедневное наблюдение за учебно-познавательной деятельностью учащихся на занятиях.

устный опрос (индивидуальный и фронтальный, устные зачеты, экзамены и т.д.).

письменный контроль знаний и умений осуществляется с помощью письменных работ (диктанты, письменные ответы на вопросы, рефераты, решения различных задач и упражнений).

При оценке предметных результатов обучающихся могут использоваться следующие виды контроля:

Вводный – проводиться педагогом в начале учебного года для определения уровня остаточных знаний

Текущий – проводиться педагогом для оценки результатов повседневной работы с целью анализа хода формирования системы предметных знаний и принятия необходимых мер к устранению причин отставания. Проводится в соответствии с календарно-тематическим планированием по окончании изучения раздела или темы.

Административный контроль (аудит) – проводиться независимой административной группой для оценки соответствия предметных знаний учащегося требованиям государственного образовательного стандарта для каждой ступени (класса) каждого уровня общего образования, проводится один раз в полугодие.

Промежуточный - проводится педагогом для оценки результатов обучения за определенный период - четверть, полугодия, год.

     Методы и формы контроля:

Устный контроль - проверка знаний в форме воспроизведения изученного, умения обосновывать отдельные понятия и законы, делать выводы, применять правила. При этом могут использоваться различные формы, в том числе:

- фронтальный опрос (опрашивается весь класс)

- индивидуальная форма (ответ ученика на один или серию вопросов);

- взаимный опрос (ученики среднего звена по очереди формулируют вопросы одноклассникам и сами оценивают ответ);

- групповая работа (оцениваются как предметные умения так личностные и метапредментые результаты);

- самоконтроль, взаимоконтроль.

Письменный контроль - осуществляется в ограниченные сроки. При этом используются разнообразные формы, в том числе:

1.      самостоятельная работа (письменная проверка по небольшой теме на 15-20 минут); Могут проводиться фронтально, выборочно, индивидуально.

2.      контрольная работа - используется при фронтальном, текущем и итоговом контроле с целью проверки предметных знаний по завершенному разделу программы (темы).

3.      тестирование - проверка по полностью изученной теме или всем темам, изученными за полугодие, год по специально подготовленным заданиям (тестам) с выборочным ответом или свободным ответом.

4.      зачет (зачетная работа) - контроль  в устной или письменной форме по итогам изучения ряда тем учебной программы. При этом используется безотметочная или пятибалльная системы оценки.

5.      практической работы – контроль усвоения практической части предмета (темы, раздела) – лабораторная работа, практическая работа.

                                          Содержание тем учебного курса

1.Числа и вычисления  (5 часов)

  Дроби обыкновенные и десятичные, переход от одной формы записи дробей к другой. Понятие рационального числа, запись, сравнение, упорядочивание рациональных чисел. Арифметические действия с рациональными числами. Решение задач из реальной практики на части, на дроби.

  Степень с натуральным показателем: определение, преобразование выражений на основе определения, запись больших чисел. Проценты, запись процентов в виде дроби и дроби в виде процентов. Три основные задачи на проценты, решение задач из реальной практики. Применение признаков делимости, разложение на множители натуральных чисел. Реальные зависимости, в том числе прямая и обратная пропорциональности.

2.Начальные понятия геометрии. ( 2 часа)

Точка, прямая, отрезок, луч. Угол. Виды углов. Вертикальные и смежные углы. Биссектриса угла. Ломаная, многоугольник. Параллельность и перпендикулярность прямых.

3.Представление данных в виде таблиц, диаграмм, графиков.( 2 часа)

 Заполнение таблиц, чтение и построение диаграмм (столбиковых (столбчатых) и круговых). Чтение графиков реальных процессов. Извлечение информации из диаграмм и таблиц, использование и интерпретация данных.

4.Алгебраические выражения (5 часов)

  Переменные, числовое значение выражения с переменной. Допустимые значения переменных. Представление зависимости между величинами в виде формулы. Вычисления по формулам. Преобразование буквенных выражений, тождественно равные выражения, правила преобразования сумм и произведений, правила раскрытия скобок и приведения подобных слагаемых.Свойства степени с натуральным показателем.Одночлены и многочлены. Степень многочлена. Сложение, вычитание, умножение многочленов. Формулы сокращённого умножения: квадрат суммы и квадрат разности. Формула разности квадратов. Разложение многочленов на множители.

5.Треугольник. (3 часа)

 Равнобедренный и равносторонний треугольники. Неравенство треугольника.Свойства и признаки равнобедренного треугольника.  Признаки равенства треугольников.

6.Описательная статистика. (1 час)

 Описательная статистика: среднее арифметическое, медиана, размах, наибольшее и наименьшее значения набора числовых данных. Примеры случайной изменчивости.

7.Уравнения и неравенства (5 часов)

  Уравнение, корень уравнения, правила преобразования уравнения, равносильность уравнений.Линейное уравнение с одной переменной, число корней линейного уравнения, решение линейных уравнений. Составление уравнений по условию задачи. Решение текстовых задач с помощью уравнений. Линейное уравнение с двумя переменными и его график. Система двух линейных уравнений с двумя переменными. Решение систем уравнений способом подстановки. Примеры решения текстовых задач с помощью систем уравнений.

8.Параллельные прямые. (3 часа)

Свойства и признаки параллельных прямых. Сумма углов треугольника. Внешние углы треугольника

9.Функции (5 часов)

Координата точки на прямой. Числовые промежутки. Расстояние между двумя точками координатной прямой.

Прямоугольная система координат, оси Ox и Oy. Абсцисса и ордината точки на координатной плоскости. Примеры графиков, заданных формулами. Чтение графиков реальных зависимостей. Понятие функции. График функции. Свойства функций. Линейная функция, её график. График функции y = |x|. Графическое решение линейных уравнений и систем линейных уравнений.

10. Прямоугольный треугольник (3 часа)

  Прямоугольный треугольник. Свойство медианы прямоугольного треугольника, проведённой к гипотенузе. Признаки равенства прямоугольных треугольников. Прямоугольный треугольник с углом в 30°.

                                      Планируемые результаты усвоения

Программа обеспечивает достижение обучающимися следующих личностных, метапредметных и предметных результатов.

Личностные результаты освоения программы учебного курса «Математика» характеризуются:

1) патриотическое воспитание:

проявлением интереса к прошлому и настоящему российской математики, ценностным отношением к достижениям российских математиков и российской математической школы, к использованию этих достижений в других науках и прикладных сферах;

2) гражданское и духовно-нравственное воспитание:

готовностью к выполнению обязанностей гражданина и реализации его прав, представлением о математических основах функционирования различных структур, явлений, процедур гражданского общества (например, выборы, опросы), готовностью к обсуждению этических проблем, связанных с практическим применением достижений науки, осознанием важности морально-этических принципов в деятельности учёного;

3) трудовое воспитание:

установкой на активное участие в решении практических задач математической направленности, осознанием важности математического образования на протяжении всей жизни для успешной профессиональной деятельности и развитием необходимых умений, осознанным выбором и построением индивидуальной траектории образования и жизненных планов с учётом личных интересов и общественных потребностей;

4) эстетическое воспитание:

способностью к эмоциональному и эстетическому восприятию математических объектов, задач, решений, рассуждений, умению видеть математические закономерности в искусстве;

5) ценности научного познания:

ориентацией в деятельности на современную систему научных представлений об основных закономерностях развития человека, природы и общества, пониманием математической науки как сферы человеческой деятельности, этапов её развития и значимости для развития цивилизации, овладением языком математики и математической культурой как средством познания мира, овладением простейшими навыками исследовательской деятельности;

6) физическое воспитание, формирование культуры здоровья и эмоционального благополучия:

готовностью применять математические знания в интересах своего здоровья, ведения здорового образа жизни (здоровое питание, сбалансированный режим занятий и отдыха, регулярная физическая активность), сформированностью навыка рефлексии, признанием своего права на ошибку и такого же права другого человека;

7) экологическое воспитание:

ориентацией на применение математических знаний для решения задач в области сохранности окружающей среды, планирования поступков и оценки их возможных последствий для окружающей среды, осознанием глобального характера экологических проблем и путей их решения;

8) адаптация к изменяющимся условиям социальной и природной среды:

готовностью к действиям в условиях неопределённости, повышению уровня своей компетентности через практическую деятельность, в том числе умение учиться у других людей, приобретать в совместной деятельности новые знания, навыки и компетенции из опыта других;

необходимостью в формировании новых знаний, в том числе формулировать идеи, понятия, гипотезы об объектах и явлениях, в том числе ранее неизвестных, осознавать дефициты собственных знаний и компетентностей, планировать своё развитие;

способностью осознавать стрессовую ситуацию, воспринимать стрессовую ситуацию как вызов, требующий контрмер, корректировать принимаемые решения и действия, формулировать и оценивать риски и последствия, формировать опыт.

Метапредметные результаты

  Познавательные универсальные учебные действия

Базовые логические действия:

·         выявлять и характеризовать существенные признаки математических объектов, понятий, отношений между понятиями, формулировать определения понятий, устанавливать существенный признак классификации, основания для обобщения и сравнения, критерии проводимого анализа;

·         воспринимать, формулировать и преобразовывать суждения: утвердительные и отрицательные, единичные, частные и общие, условные;

·         выявлять математические закономерности, взаимосвязи и противоречия в фактах, данных, наблюдениях и утверждениях, предлагать критерии для выявления закономерностей и противоречий;

·         делать выводы с использованием законов логики, дедуктивных и индуктивных умозаключений, умозаключений по аналогии;

·         разбирать доказательства математических утверждений (прямые и от противного), проводить самостоятельно несложные доказательства математических фактов, выстраивать аргументацию, приводить примеры и контрпримеры, обосновывать собственные рассуждения;

·         выбирать способ решения учебной задачи (сравнивать несколько вариантов решения, выбирать наиболее подходящий с учётом самостоятельно выделенных критериев).

Базовые исследовательские действия:

·         использовать вопросы как исследовательский инструмент познания, формулировать вопросы, фиксирующие противоречие, проблему, самостоятельно устанавливать искомое и данное, формировать гипотезу, аргументировать свою позицию, мнение;

·         проводить по самостоятельно составленному плану несложный эксперимент, небольшое исследование по установлению особенностей математического объекта, зависимостей объектов между собой;

·         самостоятельно формулировать обобщения и выводы по результатам проведённого наблюдения, исследования, оценивать достоверность полученных результатов, выводов и обобщений;

·         прогнозировать возможное развитие процесса, а также выдвигать предположения о его развитии в новых условиях.

Работа с информацией:

·         выявлять недостаточность и избыточность информации, данных, необходимых для решения задачи;

·         выбирать, анализировать, систематизировать и интерпретировать информацию различных видов и форм представления;

·         выбирать форму представления информации и иллюстрировать решаемые задачи схемами, диаграммами, иной графикой и их комбинациями;

·         оценивать надёжность информации по критериям, предложенным учителем или сформулированным самостоятельно.

Коммуникативные универсальные учебные действия:

·         воспринимать и формулировать суждения в соответствии с условиями и целями общения, ясно, точно, грамотно выражать свою точку зрения в устных и письменных текстах, давать пояснения по ходу решения задачи, комментировать полученный результат;

·         в ходе обсуждения задавать вопросы по существу обсуждаемой темы, проблемы, решаемой задачи, высказывать идеи, нацеленные на поиск решения, сопоставлять свои суждения с суждениями других участников диалога, обнаруживать различие и сходство позиций, в корректной форме формулировать разногласия, свои возражения;

·         представлять результаты решения задачи, эксперимента, исследования, проекта, самостоятельно выбирать формат выступления с учётом задач презентации и особенностей аудитории;

·         понимать и использовать преимущества командной и индивидуальной работы при решении учебных математических задач;

·         принимать цель совместной деятельности, планировать организацию совместной работы, распределять виды работ, договариваться, обсуждать процесс и результат работы, обобщать мнения нескольких людей;

·         участвовать в групповых формах работы (обсуждения, обмен мнениями, мозговые штурмы и другие), выполнять свою часть работы и координировать свои действия с другими членами команды, оценивать качество своего вклада в общий продукт по критериям, сформулированным участниками взаимодействия.

Регулятивные универсальные учебные действия

Самоорганизация:

·         самостоятельно составлять план, алгоритм решения задачи (или его часть), выбирать способ решения с учётом имеющихся ресурсов и собственных возможностей, аргументировать и корректировать варианты решений с учётом новой информации.

Самоконтроль, эмоциональный интеллект:

·         владеть способами самопроверки, самоконтроля процесса и результата решения математической задачи;

·         предвидеть трудности, которые могут возникнуть при решении задачи, вносить коррективы в деятельность на основе новых обстоятельств, найденных ошибок, выявленных трудностей;

·         оценивать соответствие результата деятельности поставленной цели и условиям, объяснять причины достижения или недостижения цели, находить ошибку, давать оценку приобретённому опыту.

Предметные результаты

   К концу обучения в 7 классе обучающийся получит следующие предметные результаты:

Числа и вычисления

Выполнять, сочетая устные и письменные приёмы, арифметические действия с рациональными числами.

Находить значения числовых выражений, применять разнообразные способы и приёмы вычисления значений дробных выражений, содержащих обыкновенные и десятичные дроби.

Переходить от одной формы записи чисел к другой (преобразовывать десятичную дробь в обыкновенную, обыкновенную в десятичную, в частности в бесконечную десятичную дробь).

Сравнивать и упорядочивать рациональные числа.

Округлять числа.

Выполнять прикидку и оценку результата вычислений, оценку значений числовых выражений. Выполнять действия со степенями с натуральными показателями.

Применять признаки делимости, разложение на множители натуральных чисел.

Решать практико-ориентированные задачи, связанные с отношением величин, пропорциональностью величин, процентами, интерпретировать результаты решения задач с учётом ограничений, связанных со свойствами рассматриваемых объектов.

Алгебраические выражения

Использовать алгебраическую терминологию и символику, применять её в процессе освоения учебного материала.

Находить значения буквенных выражений при заданных значениях переменных.

Выполнять преобразования целого выражения в многочлен приведением подобных слагаемых, раскрытием скобок.

Выполнять умножение одночлена на многочлен и многочлена на многочлен, применять формулы квадрата суммы и квадрата разности.

Осуществлять разложение многочленов на множители с помощью вынесения за скобки общего множителя, группировки слагаемых, применения формул сокращённого умножения.

Применять преобразования многочленов для решения различных задач из математики, смежных предметов, из реальной практики.

Использовать свойства степеней с натуральными показателями для преобразования выражений.

Уравнения и неравенства

Решать линейные уравнения с одной переменной, применяя правила перехода от исходного уравнения к равносильному ему. Проверять, является ли число корнем уравнения.

Применять графические методы при решении линейных уравнений и их систем.

Подбирать примеры пар чисел, являющихся решением линейного уравнения с двумя переменными.

Строить в координатной плоскости график линейного уравнения с двумя переменными, пользуясь графиком, приводить примеры решения уравнения.

Решать системы двух линейных уравнений с двумя переменными, в том числе графически.

Составлять и решать линейное уравнение или систему линейных уравнений по условию задачи, интерпретировать в соответствии с контекстом задачи полученный результат.

Функции

Изображать на координатной прямой точки, соответствующие заданным координатам, лучи, отрезки, интервалы, записывать числовые промежутки на алгебраическом языке.

Отмечать в координатной плоскости точки по заданным координатам, строить графики линейных функций. Строить график функции y = |х|.

Описывать с помощью функций известные зависимости между величинами: скорость, время, расстояние, цена, количество, стоимость, производительность, время, объём работы.

Находить значение функции по значению её аргумента.

Понимать графический способ представления и анализа информации, извлекать и интерпретировать информацию из графиков реальных процессов и зависимостей.

К концу обучения в 7 классе (геометрия) обучающийся получит следующие предметные результаты:

          Распознавать изученные геометрические фигуры, определять их взаимное расположение, изображать геометрические фигуры, выполнять чертежи по условию задачи. Измерять линейные и угловые величины. Решать задачи на вычисление длин отрезков и величин углов.

Делать грубую оценку линейных и угловых величин предметов в реальной жизни, размеров природных объектов. Различать размеры этих объектов по порядку величины.

Строить чертежи к геометрическим задачам.

Пользоваться признаками равенства треугольников, использовать признаки и свойства равнобедренных треугольников при решении задач.

Проводить логические рассуждения с использованием геометрических теорем.

Пользоваться признаками равенства прямоугольных треугольников, свойством медианы, проведённой к гипотенузе прямоугольного треугольника, в решении геометрических задач.

Определять параллельность прямых с помощью углов, которые образует с ними секущая. Определять параллельность прямых с помощью равенства расстояний от точек одной прямой до точек другой прямой.

Решать задачи на клетчатой бумаге.

Проводить вычисления и находить числовые и буквенные значения углов в геометрических задачах с использованием суммы углов треугольников и многоугольников, свойств углов, образованных при пересечении двух параллельных прямых секущей. Решать практические задачи на нахождение углов.

Владеть понятием геометрического места точек. Уметь определять биссектрису угла и серединный перпендикуляр к отрезку как геометрические места точек.

Формулировать определения окружности и круга, хорды и диаметра окружности, пользоваться их свойствами. Уметь применять эти свойства при решении задач.

Владеть понятием описанной около треугольника окружности, уметь находить её центр. Пользоваться фактами о том, что биссектрисы углов треугольника пересекаются в одной точке, и о том, что серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.

Владеть понятием касательной к окружности, пользоваться теоремой о перпендикулярности касательной и радиуса, проведённого к точке касания.

Пользоваться простейшими геометрическими неравенствами, понимать их практический смысл.

Проводить основные геометрические построения с помощью циркуля и линейки.

К концу обучения в 7 классе (вероятность и статистика) обучающийся получит следующие предметные результаты:

          Читать информацию, представленную в таблицах, на диаграммах, представлять данные в виде таблиц, строить диаграммы (столбиковые (столбчатые) и круговые) по массивам значений.

Описывать и интерпретировать реальные числовые данные, представленные в таблицах, на диаграммах, графиках.

Использовать для описания данных статистические характеристики: среднее арифметическое, медиана, наибольшее и наименьшее значения, размах.

Иметь представление о случайной изменчивости на примерах цен, физических величин, антропометрических данных, иметь представление о статистической устойчивости.

Календарно-тематическое планирование по математике 7 Г класс 2025-2026 учебный год 1 час в неделю (34 часов в год)

УЧЕБНО-МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ОБРАЗОВАТЕЛЬНОГО ПРОЦЕССА . ОБЯЗАТЕЛЬНЫЕ УЧЕБНЫЕ МАТЕРИАЛЫ ДЛЯ УЧЕНИКА

Алгебра : 7 класс: учебник/Ю.Н. Макарычев ,  Н.Г. Миндюк и др. М.: Просвещение, 2023;

Геометрия : 7 класс: учебник/Л.С.Атанасян , В.Ф. Бутузов  и др. М.: Просвещение, 2023

Вероятность и статистика . Базовый уровень.: 7-9 классы: учебник в двух частях /И.Р.Высоцкий , И.В. Ященко и др. М.: Просвещение, 2023

   МЕТОДИЧЕСКИЕ МАТЕРИАЛЫ ДЛЯ УЧИТЕЛЯ

1. Геометрия : 7 класс: рабочая тетрадь/Л.С.Атанасян , В.Ф. Бутузов  и др. М.: Просвещение, 2014

2. Дидактические материалы по математике. 7 класс. К учебнику Л.С.Атанасян , В.Ф. Бутузов  и др. М.: Просвещение, 2014 

3. Достижение метапредметных результатов в рамках изучения предметов математического блока (основное общее образование) : методические рекомендации / Л.О. Рослова, Е.Е. Алексеева, Е.В. Буцко ; под ред. Л.О. Рословой. – ФГБНУ «Институт стратегии развития образования», 2023. – 73 с.: ил.

4. Математика (углубленный уровень). Реализация требований ФГОС среднего общего образования : методическое пособие для учителя / Л.О. Рослова, Е.Е. Алексеева, Е.В. Буцко ; под ред. Л.О. Рословой. – ФГБНУ «Институт стратегии развития образования», 2023. – 92 с.: ил.

5. Сборник типовых заданий для текущего оценивания по учебным предметам «Математика и «Информатика» : методические рекомендации / Т.В. Расташанская, Е.А. Баракова, А.С. Городенская. – М. : ФГБНУ «Институт содержания и методов обучения», 2024. – 94 с.: ил.

6. Система оценки достижений планируемых предметных результатов освоения учебного предмета «Математика». Среднее общее образование : методические рекомендации / Л.О. Рослова, Е.Е. Алексеева, Е.В. Буцко, И.И. Карамова ; под ред. Л.О. Рословой. – М. : ФГБНУ «Институт содержания и методов обучения», 2024. – 37 с.: ил.

7. Достижение метапредметных результатов в рамках изучения предметов математического блока (основное общее образование) : методические рекомендации / Л.О. Рослова, Е.Е. Алексеева, Е.В. Буцко ; под ред. Л.О. Рословой. – ФГБНУ «Институт стратегии развития образования», 2023. – 73 с.: ил.

ЦИФРОВЫЕ ОБРАЗОВАТЕЛЬНЫЕ РЕСУРСЫ И РЕСУРСЫ СЕТИ ИНТЕРНЕТ

1. Методические видеоуроки. – URL: https://edsoo.ru/metodicheskie_videouroki/

2. Методические семинары / Математика. – URL: https://edsoo.ru/metodicheskie-seminary/ms-matematika/

3. Библиотека ЦОК

Электронные издания

Журнал "Квант"

Журнал "Наука и жизнь"

Энциклопедия "Кругосвет"

Коллекции

Геометрическое конструирование на плоскости и в пространстве

История математики

Олимпиадные задачи по всем разделам  математики

Памятники науки и техники в собрании Политехнического музея

Словарь-справочник понятий и фактов элементарной математики

Электронная библиотека учебно-методической литературы по математике

Инструменты организации учебного процесса

  Платформа «1С Образование»

  GeoGebra

  MAX

   Образовательный сайт «Решу ВПР»

                                                                   Контрольно-измерительные материалы

Оценка письменных работ обучающихся по алгебре

Отметка «5» ставится, если:

- работа выполнена полностью;

- в логических рассуждениях и обосновании решения нет пробелов и ошибок;

- в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).

Отметка «4» ставится, если:

- работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);

- допущены одна ошибка или есть два-три недочета в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).

Отметка «3» ставится, если:

- допущено более одной ошибки или более двух-трех недочетов в выкладках, рисунках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме;

- выполнено 2/3 от объема предложенных заданий.

Отметка «2» ставится, если:

- допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.

Контрольные работы для детей с ОВЗ: дети выполняют с 1по 3 задание в контрольных работах, где 5-6 заданий и с 1 по 4 в контрольных работах, где более 6 заданий.

Контрольно-измерительные материалы составлены по следующему пособию: Алгебра : 7 класс: учебник/Ю.Н. Макарычев ,  Н.Г. Миндюк и др. М.: Просвещение, 2023;

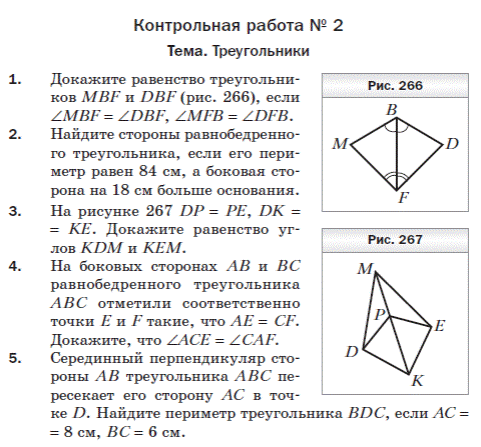
Контрольная работа №1

«Линейное уравнение с одной переменной»

Вариант 1

Вариант 2

Контрольная работа №2

«Степень с натуральным показателем. Одночлены. Многочлены. Сложение и вычитание многочленов»

Вариант 1

Вариант 2

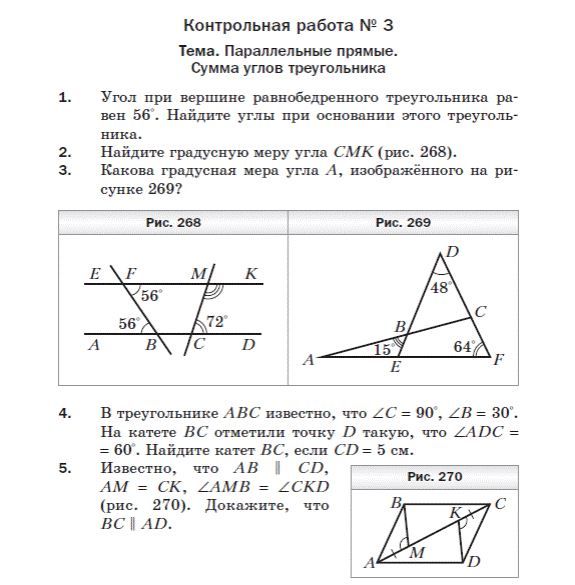
Контрольная работа №3

«Умножение одночлена на многочлен. Умножение многочлена на многочлен. Разложение многочленов на множители»

Вариант 1

Вариант 2

Контрольная работа №4

«Формулы сокращенного умножения»

Вариант 1

Вариант 2

Контрольная работа №5

«Сумма и разность кубов двух выражений. Применение различных способов разложения многочлена на многочлен»

Вариант 1

Вариант 2

Контрольная работа №6

«Функции»

Вариант 1

Вариант 2

Контрольная работа №7

«Системы линейных уравнений с двумя переменными»

Вариант 1

Вариант 2

Контрольная работа №8

«Системы линейных уравнений с двумя переменными»

Вариант 1

Вариант 2

Вариант 1

Вариант 2

Вариант 1

Вариант 2

Вариант 1

Вариант 2

Вариант 1

Вариант 2

Вариант 1

Вариант 2

Скачано с www.znanio.ru