МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ  РЕСПУБЛИКИ САХА (ЯКУТИЯ)

ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ПРОФЕССИОНАЛЬНОЕ

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ РЕСПУБЛИКИ САХА (ЯКУТИЯ)

«РЕГИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ КОЛЛЕДЖ В Г.МИРНОМ»

МЕТОДИЧЕСКОЕ ПОСОБИЕ по выполнению практических работ по дисциплине «Основы программирования и базы данных»

Составитель:

Касаткина Т.Е.., преподаватель 

ГАПОУ РС (Я) «МРТК»

г. Мирный, 2020 г.

Пояснительная записка

Практический практикум содержит методические указания и задания практических работ, а также справочный материал. Данный практикум подходит как для  самостоятельного или углубленного изучения,  так  и  для  проведения аудиторных практический занятий  по теме «Информационно-логические основы ЭВМ» дисциплины ПД 2. «Информатика» студентов всех специальностей.  

Приступая к выполнению практической работе, необходимо внимательно прочитать цель работы, ознакомиться с требованиями к уровню подготовки в соответствии с федеральными государственными стандартами, краткими теоретическими сведениями, выполнить задания работы, ответить на контрольные вопросы для закрепления теоретического материала и сделать выводы. 

 Отчет о практической работе необходимо выполнить и сдать в срок, установленный преподавателем. 

 Наличие положительной оценки по практическим работам необходимо для получения зачета по дисциплине «Информатика» и допуска к экзамену, поэтому в случае отсутствия студента на уроке по любой причине или получения неудовлетворительной оценки за лабораторную необходимо найти время для ее выполнения или пересдачи.

Правила выполнения практических работ

1.             Студент должен прийти на занятие подготовленным к выполнению практической работы.

2.             После проведения практической работы студент должен представить отчет о проделанной работе.

3.             Отчет о проделанной работе следует выполнять на листах формата А4 с одной стороны листа.

Оценку по практической работе студент получает, если:

-                 студентом работа выполнена в полном объеме;

-                 студент может пояснить выполнение любого этапа работы;

-                 отчет выполнен в соответствии с требованиями к выполнению работы;

-                 студент отвечает на контрольные вопросы на удовлетворительную оценку и выше.  Зачет по выполнению практических работ студент получает при условии выполнения всех предусмотренных программой практических работ после сдачи журнала с отчетами по работам и оценкам.

Внимание! Если в процессе подготовки к практическим работам или при решении задач возникают вопросы, разрешить которые самостоятельно не удается, необходимо обратиться к преподавателю для получения разъяснений или указаний в дни проведения дополнительных занятий. 

Порядок выполнения отчета по практической работе

1.             Ознакомиться с теоретическим материалом по практической работе.

2.             Выполнить предложенное задание согласно варианту по списку группы.

3.             Продемонстрировать результаты выполнения предложенных заданий преподавателю.

4.             Составить отчет по практической работе.

5.             Записать выводы о проделанной работе.

6.             Ответить на контрольные вопросы.

1. ПОНЯТИЕ ИНФОРМАЦИИ

Слово “информация” происходит от латинского слова  informatio, что в переводе означает сведение, разъяснение, ознакомление. 

Понятие “информация” в курсе информатики является базовым (основным), его нельзя дать через другие, более простые понятия. В геометрии, например, базовыми являются понятия: “точка”, “луч”, “плоскость”. Содержание базовых понятий в любой науке поясняется на примерах или выявляется путем сопоставления с содержанием других понятий.

Информация – это сведения об окружающем мире, которые повышают уровень осведомленности человека.

Свойства информации.

1.      Понятность (на понятном языке, понятными терминами)

2.      Полезность (информация должна иметь практическую ценность)

3.      Достоверность (информация должна быть правдивой)

4.      Актуальность (своевременность)

5.      Полнота (информация полна, если ее достаточно для принятия решений)

6.      Точность (определяется степенью близости к реальному состоянию объекта, процесса, явления)

Понятие информационного процесса.

Действия, выполняемые с информацией, называются информационными процессами.

Выделяют следующие информационные процессы:

1.              Процесс передачи информации, который включает в себя:

 ввод (сбор, получение) информации;  вывод информации;  передачу информации.

2.              Процесс обработки (преобразования) информации

3.              Процесс хранения информации (в собственной памяти, или на внешних носителях)  Примеры информационных процессов помещены в Таблице 1. Таблица 1. Примеры информационных процессов.

1.1.Единицы измерения информации.

Содержательный подход к измерению информации.

За единицу измерения информации принимается 1 бит - такое количество информации, которое содержит сообщение, уменьшающее неопределенность знаний в два раза.

Что такое неопределенность знаний? Поясним на примере.

Допустим, вы бросаете монету, загадывая: орел или решка? Любой из вариантов ответа уменьшает неопределенность в 2 раза и, следовательно, количество информации равно 1 биту. 

Количество информации (i), содержащееся в сообщении о том, что произошло одно из N равновесных событий, определяется из решения уравнения: 

(1)

Прологарифмировав равенство (1) по основанию 2, получим: i*log₂2= log₂N, следовательно,

(2)

1.1.Алфавитный подход к измерению информации

Алфавитный подход к измерению информации не связывает количество информации с содержательным сообщением. Рассмотрим этот подход на примере текста, написанного на каком-нибудь языке, например, на русском. Все множество используемых в языке символов будем называть алфавитом. Полное количество символов алфавита будем называть мощность алфавита.  

Например, в алфавит мощностью N=256 символов можно поместить все необходимые символы: латинские и русские буквы, цифры, знаки арифметических операций, знаки препинания и т.д.  Представим себе, что текст, состоящий из 256 символов, поступает последовательно, и в каждый момент времени может появиться любой из них. Тогда по формуле (1):

2ⁱ = 256, →  i=8 (бит)

Таким образом, один символ алфавита мощностью 256 символов, “весит” 8 бит. Поскольку 8 бит – часто встречающаяся величина, ей присвоили свое название 1 байт:

(3)

Чтобы подсчитать количество информации на одной странице текста, необходимо:

количество символов в строке умножить на количество строк на листе. Так, например, если взять страницу текста, содержащую 40 строк по 60 символов в каждой строке, то одна страница такого текста будет содержать 

60*40=2400 (байт информации)

Если требуется подсчитать количество информации, содержащееся в книге из 160 страниц, нужно

2400*160=384000 (байт) 

Уже на этом примере видно, что байт – достаточно мелкая единица. Для измерения больших объемов информации используются следующие производные от байта единицы:

(4)

Задание 1. 

В алфавите формального (искусственного) языка всего два знака-буквы («+» и «-»). Каждое слово этого языка состоит из двух букв. Максимальное число слов этого языка:

Решение.

Решение задачи сводится к поиску количества (N) комбинаций строк длиной (i) 2 символа, составленных из 2 знаков. Следовательно, используя формулу 2ⁱ = N, получаем 2² =

4.

Ответ: 1.

Задание 2. 

Алфавит племени содержит всего 8 букв. Какое количество информации несет одна буква этого алфавита?

Решение.

Мощность алфавита племени – 8 букв. Применим формулу 2^х = N, где N – мощность алфавита, х – количество бит на один символ алфавита. 2^х =8, х=3 бит, что соответствует варианту ответа №3. Ответ: 3.

Задание 3. 

Если вариант теста в среднем имеет объем 20 килобайт (на каждой странице теста 40 строк по 64 символа в строке, 1 символ занимает 8 бит), то количество страниц в тесте равно:

Решение.

Известен информационный объем теста и информационный «вес» одного символа в нем. Найдем объем одной страницы: 40*64*8 бит.  20 Кбайт = 20*1024 байт = 20*1024*8 бит. Найдем количество страниц: 20*1024*8/(40*64*8) = 8 (стр.) (Ответ № 4) Ответ: 4.

Задание 4. 

В пяти килобайтах:

Решение.

32Гб = 2⁵ Гб = 2⁵*2¹⁰ Мб = 2⁵*2¹⁰ *2¹⁰ Кб =2⁵*2¹⁰ *2¹⁰*2¹⁰ байт  = 2³⁵ байт, что соответствует ответу №1. Ответ: 1.

Задание 6. 

Считая, что один символ кодируется одним байтом, подсчитать в байтах количество информации, содержащееся в фразе: “Терпение и труд все перетрут.” Решение. 

В фразе 29 символов (включая точку и пробелы), 1 символ несет 1 байт информации, значит фраза содержит 29 байт. Ответ: 29.

Задание 7. (Задание А2  демоверсии 2004 г.)

Считая, что каждый символ кодируется одним байтом, оцените информационный объём предложения: «Мой дядя самых  честных правил, Когда не в шутку занемог, Он уважать себя заставил И лучше выдумать не мог.»

                      1) 108 бит                    2) 864 бит                    3) 108 килобайт           4) 864 килобайт

Решение.

Предложенная строка содержит ровно 108 символов, включая кавычки, пробелы и знаки препинания. При кодировании каждого символа одним байтом на символ будет приходиться по 8 бит, поэтому объём этого предложения составит 108 байт или 108х8=864 бит, что соответствует ответу №2.  Ответ: 2.

Задание 8. (Задание А3  демоверсии 2004 г.)

Шахматная доска состоит из 64  полей: 8 столбцов и 8 строк. Какое минимальное количество бит потребуется для кодирования координат одного шахматного поля?

Решение.

Для того, чтобы различить 64 клетки шахматного поля потребуются 64 значения двоичного кода. Поскольку 64=2⁶,  то в двоичном коде потребуется шесть разрядов. Верный ответ№3.

Ответ: 3.

Задание 9. (Задание А4  демоверсии 2004 г.)

Получено сообщение, информационный объём которого равен 32 битам. Чему равен этот объём в байтах?

Решение. 

1 байт = 8 бит, следовательно, 32/8=4, что соответствует ответу №4. Ответ: 4.

Задание 10. 

Каждое показание счётчика, фиксируемое в памяти компьютера, занимает 10 бит. Записано 100 показаний этого датчика. Каков информационный объём снятых значений в байтах?

Решение. 

10 бит*100= 1000 бит, 1 байт = 8 бит, следовательно: 1000/8=125 байт. Значит, верный ответ №3.

Ответ: 3.

Практическая работа №1

Цель работы: закрепить  практические навыки к подходам измерения информации. Задания

Вариант 1

1.             Подсчитать в килобайтах количество информации в тексте, если текст состоит из 600 символов, а мощность используемого алфавита – 128 символов.

2.             Имеется 2 текста на разных языках. Первый текст использует 32-символьный алфавит и содержит 200 символов, второй – 16-символьный алфавит и содержит 250 символов. Какой из текстов содержит большее количество информации и на сколько бит?

3.             Сообщение занимает 2 страницы и содержит  килобайта информации. На каждой странице записано 256 символов. Какова мощность использованного алфавита? 2. Сравните (поставьте знак отношения)  200 байт и 0,25 Кбайт.  3 байта и 24 бита.

•     1536 бит и 1,5 Кбайта.

•     1000 бит и 1 Кбайт.  8192 байта и 1 Кбайт.

Вариант 2

1.             Книга, набранная с помощью компьютера, содержит 150 страниц, на каждой странице – 40 строк, в каждой строке – 60 символов. Каков объем информации в книге?

2.             Для записи сообщения использовался 64-символьный алфавит. Каждая страница содержит 30 строк. Все сообщение содержит 8775 байтов информации и занимает 6 страниц. Сколько символов в строке?

3.             Информационное сообщение объемом 4Кбайта содержит 4096 символов. Сколько символов содержит алфавит, при помощи которого было записано это сообщение? 2. Сравните (поставьте знак отношения)  200 байт и 0,25 Кбайт.  3 байта и 24 бита.

•     1536 бит и 1,5 Кбайта.

•     1000 бит и 1 Кбайт.  8192 байта и 1 Кбайт.

Вариант 3

1.    Для записи текста использовался 256-символьный алфавит. Каждая страница содержит 30 строк по 70 символов в строке. Какой объем информации содержит 5 страниц текста?

2.    Для записи текста использовался 256-символьный алфавит. Каждая страница содержит 30 строк по 70 символов в строке. Какой объем информации содержит 5 страниц текста?

3.    Сколько Килобайтов составляет сообщение из 512 символов 16-символьного алфавита?

2. Сравните (поставьте знак отношения)  200 байт и 0,25 Кбайт.  3 байта и 24 бита.

•     1536 бит и 1,5 Кбайта.

•     1000 бит и 1 Кбайт.  8192 байта и 1 Кбайт.

Вариант 4

1.             Можно ли уместить на одну дискету книгу, имеющую 432 страницы, причем на каждой странице этой книги 46 строк, а в каждой строке 62 символа?

2.             Сколько символов в тексте, если мощность алфавита – 64 символа, а объем информации, содержащейся в нем – 1,5 Кбайта?

3.             Сообщение, набранное с помощью компьютера, занимает 3 страницы по 25 строк. В каждой строке записано по 60 символов. Сколько символов в использованном алфавите, если все сообщение содержит 1125 байтов?

2. Сравните (поставьте знак отношения)  200 байт и 0,25 Кбайт.  3 байта и 24 бита.

•     1536 бит и 1,5 Кбайта.

•     1000 бит и 1 Кбайт.  8192 байта и 1 Кбайт.

Вариант 5

1.             Одно племя имеет 32-символьный алфавит, а второе племя – 64-символьный алфавит. Вожди племен обменялись письмами. Письмо первого племени содержало 80 символов, а письмо второго племени – 70 символов. Сравните объем информации, содержащийся в письмах.

2.             Сообщение занимает 4 страницы и содержит 1/16Кбайта информации. На каждой странице записано 128 символов. Сколько символов содержит используемый алфавит?

3.             Книга, набранная с помощью компьютера, содержит 50 страниц, на каждой странице - 16строк, в каждой строке - 64 символов. Каков объем информации в книге?

2. Сравните (поставьте знак отношения)  200 байт и 0,25 Кбайт.  3 байта и 24 бита.

•     1536 бит и 1,5 Кбайта.

•     1000 бит и 1 Кбайт.

•     8192 байта и 1 Кбайт.

Дополнительные задания

1.    Сообщение, записанное буквами из 64-х символьного алфавита, содержит 20 символов.

Какой объем информации оно несет?

2.    Информационное сообщение объемом 1,5 Кбайта содержит 3072 символа. Сколько символов содержит алфавит, при помощи которого было записано это сообщение?        

3.    Сообщение занимает 3 страницы по 25 строк. В каждой строке записано по 60 символов. Сколько символов в использованном алфавите, если все сообщение содержит 1125 байтов?

4.    Для записи сообщения использовался 64-х символьный алфавит. Каждая страница содержит 30 строк. Все  сообщение содержит 8775 байтов информации и занимает 6 страниц. Сколько символов в строке?

5.    Сообщение занимает 2 страницы и содержит 1/16 Кбайта информации. На каждой странице записано 256 символов. Какова мощность использованного алфавита?

6.    Каков  информационный объем сообщения: «Встреча назначена на сентябрь» (в байтах, в битах)?

Контрольные вопросы

1.    Перечислите известные вам свойства информации.

2.    Приведите примеры получения и использования информации человеком.

3.    Укажите известные вам единицы измерения информации.

4.    Опишите известные вам способы кодирования информации.

5.    Что такое алфавит?

6.    Что такое мощность алфавита?

7.    По какой формуле связаны между собой информационный вес символа и мощность алфавита?

8.    Алфавит содержит 16 букв. Какое количество информации несет одна буква?

2  СИСТЕМА СЧИСЛЕНИЯ

2.1. Естественные и формальные языки. Язык как знаковая система.

Для обмена информацией с другими людьми человек использует естественные языки (русский, английский, китайский и др.), т.е. информация представляется с помощью естественных языков.

В основе естественного языка лежит алфавит – набор знаков, которые различаются человеком по их начертанию. В основе русского языка лежит кириллица, содержащая 33 знака, английский язык использует латинский алфавит (26 знаков), китайский язык использует алфавит из десятков тысяч знаков (иероглифов).

В соответствии с правилами грамматики из последовательности символов строят основные объекты языка – слова. Из слов в соответствии с правилами синтаксиса строят предложения. 

В естественных языках грамматика и синтаксис языка формулируются с помощью большого числа правил, из которых есть исключения, т.к. правила складывались исторически.

Наряду с естественными языками были разработаны формальные (иногда говорят, искусственные) языки (системы счисления, язык алгебры, языки программирования и т.д.). Основное отличие формальных от естественных языков состоит в наличии строгих правил грамматики и синтаксиса.

Например, системы счисления можно рассматривать как формальные языки, имеющие алфавит (цифры) и позволяющие не только именовать и записывать объекты

(числа), но и выполнять над ними арифметические операции по строго определенным правилам. 

Существуют формальные языки, которые в качестве знаков используют химические формулы, изображения элементов электрических схем, ноты, дорожные знаки, точки и тире (код азбуки Морзе) и т.д.

Представление информации может осуществляться с помощью формальных языков, которые являются знаковыми системами. Каждая знаковая система строится на основе определенного алфавита и правил выполнения операций над знаками.

Кодирование информации

Кодирование информации – это операция преобразования информации из одной знаковой системы в другую.

Средством кодирования служит таблица соответствия знаковых систем, которая устанавливает взаимно однозначное соответствие между знаками или группами знаков двух различных знаковых систем.

В процессе обмена информацией часто приходится производить операции кодирования и декодирования информации. Например, при вводе знака алфавита в компьютер путем нажатия соответствующей клавиши на компьютере, происходит кодирование знака, т.е. преобразование его в компьютерный код.  При выводе знака на экран монитора или принтер происходит обратный процесс – декодирование, когда из компьютерного кода знак преобразуется в его графическое изображение.  Двоичное кодирование информации.

Для представления информации в компьютере используется двоичное кодирование, т.к. технические устройства компьютера могут сохранять и распознавать не более двух различных состояний (цифр): намагничен / размагничен (участок поверхности магнитного носителя информации), отражает/не отражает (участок поверхности лазерного диска);  и т.д.

Информация на компьютере представлена в машинном коде, алфавит которого состоит из цифр (0 и 1). Каждая цифра машинного кода несет информацию в 1 бит.

2.2. Системы счисления

Система счисления – это знаковая система, в которой числа записываются по определенным правилам  с помощью символов некоторого алфавита, называемыми цифрами. Системы счисления делятся на непозиционные и позиционные. 

Непозиционная система счисления – система счисления, в которой значение цифры не зависит от ее позиции в записи числа. 

Примеры непозиционных систем счисления: унарная (единичная) система счисления, римская система счисления, алфавитная система счисления. 

 Унарная (единичная) система счисления характеризуется тем, что в ней для записи чисел применяется только один вид знаков – палочка. Каждое число в этой системе счисления обозначалось с помощью строки, составленной из палочек, количество которых равнялось обозначаемому числу. Неудобства такой системы счисления очевидны: это громоздкость записи больших чисел,  значение числа сразу не видно, чтобы его получить, нужно сосчитать палочки.

В римской системе счисления для обозначения чисел используются заглавные латинские буквы, являющиеся «цифрами» этой системы счисления:

 Число в римской системе счисления обозначается набором стоящих подряд «цифр». Значение числа равно:

1)   сумме значений идущих подряд нескольких одинаковых «цифр» (назовем их группой первого вида);

2)   разности значений большей и меньшей «цифр», если слева от большей «цифры» стоит меньшая (группа второго вида);

3)   сумме значений групп и «цифр», не вошедших в группы первого и второго видов.

Примеры. 1.  Число 32 в римской системе счисления имеет вид: XXXII = (X+X+X)+(I+I) =30+2 (две группы первого вида) 2.  Число 444 в римской системе счисления имеет вид:

CDXLIV = (D-C)+(L-X)+(V-I) (= 400 + 40 + 4 – три группы второго вида)

3. Число 1974:

MCMLXXIV = M+(M-C)+L+(X++X)+(V-I) = 1000+900+50+20+4 (наряду с группами обоих видов в формировании числа участвуют отдельные «цифры»)

4. Число 2005:

MMV = (M+M) +V = 1000+1000+5 (две группы первого вида)

Позиционные системы счисления характеризуется тем, что количественное значение цифры зависит от ее позиции в числе. Каждая позиционная система счисления имеет определенный алфавит цифр и основание, равное количеству цифр (знаков в ее алфавите). 

Наиболее     распространенными            позиционными         системами     счисления           являются десятичная, двоичная, восьмеричная и шестнадцатеричная. 

Десятичная система счисления имеет алфавит из десяти цифр: 0, 1, …, 9.

Двоичная система счисления имеет алфавит из двух цифр: 0, 1. Например, в числе 1987₁₀ цифра «1» обозначает одну тысячу (1*10³), цифра «9» обозначает девять сотен (9*10²), цифра «8» обозначает восемь десятков (8*10¹), цифра «7» обозначает семь единиц (7*10⁰). В общем виде, если запись числа в системе счисления с основанием n>1 выглядит как abcd, то само число равно значению выражения an³+bn²+cn¹+dn⁰. Перевод целого числа из двоичной системы счисления в десятичную. Пример.

101₂ = 1*2² + 0*2¹ + 1*2⁰  = 1*4 + 0 +1 = 5₁₀ Задание 11. 

Переведите число 1011012 в десятичную систему счисления. Решение.

101101₂=1*2⁵+0*2⁴+1*2³+1*2²+0*2¹+1*2⁰=32+8+4+1=45₁₀

Ответ:  101101₂=45₁₀ Перевод целого числа из десятичной системы счисления в двоичную. Алгоритм

1. Последовательно выполнить деление исходного целого десятичного числа и получаемых целых частных на основание системы (на 2) до тех пор,  пока не получится частное, меньшее делителя (т.е. меньшее 2). 2. Записать полученные остатки в обратной последовательности.

Пример.                                    Решение.

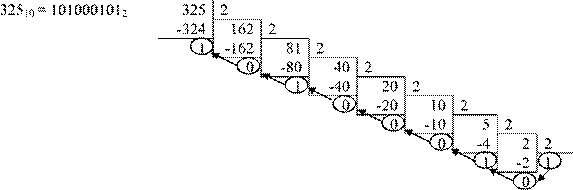
Задание 12. 

Как представляется  число 2510 в двоичной системе счисления?

Решение. 

25₁₀=10011₂, что соответствует ответу №2. Ответ: 2.

Перевод дробного числа из двоичной системы счисления в десятичную. Пример.

111,01₂  = 1*2² + 1*2¹ + 1*2⁰  + 1*2^-1 + 1*2^-2  = 1*4 + 1*2 +1+ 0*  +1*  =

 = 4+2+1+0,5+0,25 = 7,75₁₀

Перевод дробного числа из десятичной системы счисления в двоичную. Алгоритм.

1.    Последовательно умножать (в исходной системе счисления) данное число и получаемые дробные части произведений на основание новой системы  (на 2) до тех пор, пока дробная часть произведения не станет равной нулю или будет достигнута требуемая точность представления данного числа. 

2.    Полученные целые части произведений, являющиеся цифрами в числа в новой системе счисления, привести в соответствие с алфавитом новой системе счисления.

3.    Составить дробную часть числа в новой системе счисления, начиная с целой части

первого произведения. Пример. 

0,5625₁₀  = 0,1001₂.

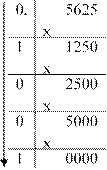
Решение.  

                                                                                                                       Очевидно,     что     этот     процесс

                           2                                                7 может бесконечности. Обрывают процесс на продолжаться                    до

                                                                                              2           шаге,    когда    получена     требуемая

2 точность                                вычисления    (количество 2            знаков после запятой) . 

2 0,7₁₀ ≈ 0,10110 ₂

2

2

2

                                                                           2

                                                             0

                                                         … 

2.3. Арифметические операции в двоичной и кратных ей системах счисления.

Арифметические операции в позиционных системах счисления производится по единому алгоритму. Так, сложение двоичных чисел происходит по классическому алгоритму «столбиком» с переносом числа, кратного двум, единицей в следующий разряд.

Рассмотрим этот алгоритм на примере двух двоичных чисел 10101012 и 1101112:

Результат сложения выглядит как 10001100₂. Проверим результат сложения, для чего переведем все числа в десятичную систему счисления:

1010101₂=85₁₀, 110111₂=55₁₀, 10001100₂=140₁₀, 85₁₀+55₁₀=140₁₀.

Двоичная система, являющаяся основой компьютерной арифметики, весьма громоздка и неудобна для использования человеком. Поэтому программисты используют две  кратные двоичной системы  счисления:  восьмеричную и шестнадцатеричную. В случае шестнадцатеричной системы арабских цифр не хватает, и в  качестве цифр  используются первые шесть заглавных букв латинского алфавита. Примеры записи натуральных чисел от 1 до 16 в четырех системах счисления помещены в Таблице 2.

Таблица 2. Примеры записи натуральных чисел от 1 до 16 в четырех системах счисления

Из Таблицы 2 видно, что в двоичной системе  запись чисел второй восьмерки (от 8 до

15) отличается от записи первой восьмерки (от 0 до 7) наличием единицы в четвертом (справа) разряде. На этом основан алгоритм перевода двоичных чисел в восьмеричные «по триадам». Для применения этого алгоритма надо разбить двоичное число на тройки цифр (считая справа) и записать вместо каждой из троек восьмеричную цифру:

10101101₂ → 10 101 101 → 255₈.

2    5    5

Крайняя левая тройка может быть неполной (как в примере), для получения полных троек можно приписать слева недостающие нули. Убедимся в правильности алгоритма:

10101101₂  → 1*2⁷+1*2⁵+1*2³+2*2¹+1*2⁰=173₁₀;  255₈ →2*2⁶+5*2³+5*2⁰=173₁₀.

Для перевода чисел из восьмеричной системы в двоичную используется обратный алгоритм: восьмеричные цифры заменяются на тройки двоичных цифр (при необходимости слева дописываются недостающие нули): 

325₈ → 3    2    5 → 11 010 101 → 11010101₂.

 011 010 101 

Для перевода чисел из двоичной системы в шестнадцатеричную используется алгоритм «по тетрадам».  Строка двоичных цифр разбивается на четверки и вместо них записываются шестнадцатеричные цифры: 10101101₂ → 1010 1101 →   AD₁₆.

                                                    А        D         

Аналогично работает и обратный алгоритм: вместо шестнадцатеричных цифр подставляются четверки двоичных цифр.

Из восьмеричной системы в шестнадцатеричную и обратно проще переводить через двоичную систему:

D5₁₆→ D 5 →1101 0101 → 11010101₂ → 11 010 101 → 325₈.

                                                    D       5                                   3       2     5

При выполнении заданий на сложение чисел разных систем счисления их нужно перевести в одну систему счисления. Лучше всего пользоваться той системой, в которой должен быть представлен результат. 

Задание 13. (Задание А6  демоверсии 2004 г.) Вычислите значение суммы в десятичной системе счисления: 102+108+1016 = ?10

Решение.

Переведем все числа в десятичную запись:

10₂+10₈+10₁₆ = (1*2¹+0*2⁰) + (1*8¹+0*8⁰) + (1*16¹+0*16⁰) = 2+8+16=26₁₀.

Ответ: 26.

Задание 14. 

Найдите сумму x+y, если x=1110101₂ , y=1011011₂. Ответ представьте в восьмеричной системе. Решение.

Найдем сумму: 1110101₂ + 1011011₂ :

1110101₂ + 1011011₂ = 11010000₂ 

Переведем получившееся число из двоичной системы счисления в восьмеричную:  11 010 000  → 320₈.

 3     2     0

Ответ: 320. Задание 15. (Задание B1  демоверсии 2004 г.)

В системе счисления с некоторым основанием число 12 записывается в виде 110. Найдите это основание.

Решение.

Обозначим искомое основание через n. Исходя из правил записи чисел в позиционных счислениях 110_n=n²+n¹+0. Составим уравнение: n²+n=12, найдем корни: n₁=-4, n₂=3. Корень n₁=-4 не подходит, так как основание системы счисления, по определению, натуральное число большее единицы. Проверим, подходит ли корень n=3: 110₃=1*3²+1*3¹+0=9+3=12₁₀

Ответ: 3.

Задание 16.

В классе 11112 девочек и 11002 мальчиков. Сколько учеников в классе? Решение.

1111₂=1*2³+1*2²+1*2¹+1*2⁰→8+4+2+1=15₁₀.

1100₂=1*2³+1*2²+0*2¹+0*2⁰→8+4=12₁₀

1510+1210=2710

Ответ: в классе 27 учеников.

Задание 17. 

В саду 100_х фруктовых деревьев, из них 33_х яблони, 22_х груши, 16_х слив и 5_х вишен. В какой системе счисления посчитаны деревья? Решение.

100_х = 33_х + 22_х + 16_х + 5_х

1*х²=3*х¹+3*х⁰+2*х¹+2*х⁰+ 1*х¹+6*х⁰+5*х⁰ х²=3х+3+2х+2+ 1х+6+5 х²-6х-16=0

D=b²-4ac=36+4*16=36+64=100

x_1,2= ^{b D} = (6±10)/2 2a x₁= - 2 – не удовлетворяет смыслу задачи, x₂= 8 – основание искомой системы счисления.

Ответ: деревья посчитаны в восьмеричной системе счисления.

Задание 18. 

Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 17 оканчивается на 2.

Решение.

Последняя цифра в записи числа представляет собой остаток от деления числа на основание системы счисления. Поскольку 17-2=15, то искомые основания систем счисления будут являться делителями 15, это: 3, 5, 15.

Проверим наш ответ, представив число 17 в соответствующих системах счисления:

17₁₀ = 1012₃                            17₁₀ = 112₅                    17₁₀ = 12₁₅

Ответ: 3, 5, 15.

Задание 19. 

В системе счисления с некоторым основанием число 17 записывается как 101. Укажите это основание.  Решение.

17₁₀ = 101_х = 1*х² + 0*х¹+ 1 х⁰

17=х²+1,→ х²=16,→ x_1,2=± 16 =±4 x₁= - 4 – не удовлетворяет смыслу задачи, x₂= 4 – основание искомой системы счисления. Ответ: 4.

2.4.Арифметические операции в позиционных системах счисления

           Арифметические операции в рассматриваемых позиционных системах счисления выполняются по законам, известным из десятичной арифметики. Двоичная система счисления имеет основание 2, и для записи чисел используются всего две цифры 0 и 1 в отличие от десяти цифр десятичной системы счисления.

Рассмотрим сложение одноразрядных чисел: 0+0=0, 0+1=1, 1+0=0. Эти равенства справедливы как для двоичной системы, так и для десятичной системы. Чему же равно 1+1? В десятичной системе это 2. Но в двоичной системе нет цифры 2! Известно, что при десятичном сложении 9+1 происходит перенос 1 в старший разряд, так как старше 9 цифры нет. То есть 9+1=10. В двоичной системе   старшей цифрой  является  1.  Следовательно,  в  двоичной  системе  1+1=10,  так  как     при сложении двух единиц происходит переполнение разряда и производится перенос в старший разряд. Переполнение разряда наступает тогда, когда значение числа в нем становится равным или большим основания. Для двоичной системы это число равно 2 (102=210).

Продолжая добавлять единицы,  заметим: 102+1=112, 112+1=1002 - произошла "цепная реакция", когда перенос единицы в один разряд вызывает перенос в следующий разряд.      Сложение многоразрядных чисел происходит по этим же правилам с учетом возможности переносов из младших разрядов в старшие.

Вычитание многоразрядных двоичных чисел производится с учетом возможных заѐмов из старших разрядов. Действия умножения и деления чисел в двоичной арифметике можно выполнять по общепринятым для позиционных систем правилам. 

Аналогичные таблицы составляются для любой позиционной системы счисления. Пользуясь такими таблицами, можно выполнять действия над многозначными числами.

Пример 1. Сложить числа:

а) 10000000100(2)+ 111000010(2)= 10111000110(2);

б) 223,2(8)+ 427,54(8)  = 652,74(8);

в) ЗВЗ,6(16)+38В,4(16)=73Е,А16).

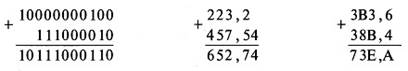
Пример 2. Выполнить умножение:

а) 100111(2)х 1000111(2) = 101011010001(2); 

б) 1170,64(8)х46,3(8) = 57334,134(8);

в) 61,А16)  х 40,D(16) = 18В7,52(16).

Практическая работа № 2

Цель работы: Повторить и закрепить знания учащихся по способам представления чисел в позиционных системах счисления, переводу чисел из десятичной системы счисления в любую другую и обратно.

Задания 

В соответствии с выданным вариантом задания преподавателем выполнить:

1.   Переведите данное число из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную системы счисления.

2.   Переведите данное число в десятичную систему счисления.

3.   Сложите числа.

4.   Выполните вычитание.

5.   Выполните умножение.

Примечание: В заданиях 3 — 5 проверьте правильность вычислений переводом исходных данных и результатов в десятичную систему счисления. В задании 1 д) получите пять знаков после запятой в двоичном представлении.

Вариант 1

Вариант 2

Вариант 3

Вариант 4

Вариант 5

Дополнительные задания 1. Как представляется число 163₁₀ в двоичной системе счисления?

2.    Переведите число 11011011₂ в десятичную систему счисления.

3.    Найдите значение суммы: 101011₂ + 231₈ = ?₈

3. Найдите значение суммы: 111011₂ + F1₁₆ = ?₂

3. Найдите значение суммы: 12₁₆ + 112₈ = ?₈

6. Найдите значение суммы: 101011₂ + 1C₁₆ = ?₁₆

Контрольные вопросы

1.   Что называется системой счисления?

2.   На какие два типа можно разделить все системы счисления?

3.   Какие системы счисления применяются в вычислительной технике: позиционные или непозиционные? Почему?

4.   Что называется основанием системы счисления?

5.   Охарактеризуйте двоичную, восьмеричную, шестнадцатеричную системы счисления:

алфавит, основание системы счисления, запись числа.

6.   По каким правилам выполняется сложение двух положительных целых чисел?

7.   Каковы правила выполнения арифметических операций в двоичной системе счисления?

8.   Для чего используется перевод чисел из одной системы счисления в другую?

9.   Сформулируйте правила перевода чисел из системы счисления с основанием р в десятичную систему счисления и обратного перевода: из десятичной системы счисления в систему счисления с основанием р. Приведите примеры.

10.             Как выполнить перевод чисел из двоичной СС в восьмеричную и обратный перевод? Из двоичной СС в шестнадцатеричную и обратно? Приведите примеры. Почему эти правила так просты?

11.             По каким правилам выполняется перевод из восьмеричной в шестнадцатеричную СС и наоборот? Приведите примеры.

3 ОСНОВЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ

Алгебра логики – это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними.

Логическое высказывание – это любое повествовательное предложение, в отношении которого можно однозначно сказать, истинно оно или ложно.

Пример 1. «3 – простое число» является высказыванием, поскольку оно истинно.

Не всякое предложение является логическим высказыванием.

Пример 2.  Предложение «Давайте пойдем в кино» не является высказыванием. 

Вопросительные и побудительные предложения высказываниями не являются.

Высказывательная форма – это повествовательное предложение, которое прямо или косвенно содержит хотя бы одну переменную и становится высказыванием, когда все переменные замещаются своими значениями.

Пример 3. «x+2>5» - высказывательная форма, которая при x>3 является истинной, иначе ложной. 

Алгебра логики рассматривает любое высказывание только с одной точки зрения – является ли оно истинным или ложным. Слова и словосочетания «не», «и», «или», «если..., то», «тогда и только тогда» и другие позволяют из уже заданных высказываний строить новые высказывания. Такие слова и словосочетания называются логическими связками. 

Высказывания, образованные из других высказываний с помощью логических связок, называются составными (сложными). Высказывания, которые не являются составными, называются элементарными (простыми).

Истинность или ложность составных высказываний зависит от истинности или ложности элементарных высказываний, из которых они состоят.

Чтобы обращаться к логическим высказываниям, им назначают имена.

Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет свое название и обозначение (таблица1.1).

Таблица 1.1 - Основные логические операции

Операция, выражаемая словом «не», называется отрицанием и обозначается чертой над высказыванием (или знаком ¬). Высказывание ¬А истинно, когда A ложно, и ложно, когда A истинно.

Операция, выражаемая связкой «и», называется конъюнкцией (лат. conjunctio – соединение) или логическим умножением и обозначается точкой « • » (может также обозначаться знаками   или &). Высказывание А • В истинно тогда и только тогда, когда оба высказывания А и В истинны. 

Операция, выражаемая связкой «или» (в неисключающем смысле этого слова), называется дизъюнкцией (лат. disjunctio – разделение) или логическим сложением и обозначается знаком  (или плюсом). Высказывание АВ ложно тогда и только тогда, когда оба высказывания А и В ложны.

Операция, выражаемая связками «если …, то», «из … следует», «... влечет …», называется импликацией(лат. implico – тесно связаны) и обозначается знаком → . Высказывание А→В ложно тогда и только тогда, когда А истинно, а В ложно.

Операция, выражаемая связками «тогда и только тогда», «необходимо и достаточно», «... равносильно …», называется эквиваленцией или двойной импликацией и обозначается знаком ↔ или ~ . Высказывание А↔В истинно тогда и только тогда, когда значения А и В совпадают.

Операция, выражаемая связками «Либо … либо», называется исключающее ИЛИ или сложением по модулю 2 и обозначается XOR или . Высказывание А В истинно тогда и только тогда, когда значения А и В не совпадают.

Импликацию можно выразить через дизъюнкцию и отрицание: .

Эквиваленцию можно выразить через отрицание, дизъюнкцию и конъюнкцию:

.

Исключающее ИЛИ можно выразить через отрицание, дизъюнкцию и конъюнкцию:

.

Операций отрицания, дизъюнкции и конъюнкции достаточно, чтобы описывать и обрабатывать логические высказывания.

Порядок выполнения логических операций задается круглыми скобками. Приоритет выполнения: отрицание, конъюнкция, дизъюнкция, исключающее или, импликация и эквиваленция.

Логическая формула - это символическая запись высказывания, состоящая из логических величин (констант или переменных), объединенных логическими операциями (связками).

Логическая функция - это функция логических переменных, которая может принимать только два значения: 0 или 1. В свою очередь, сама логическая переменная (аргумент логической функции) тоже может принимать только два значения: 0 или 1.

Пример 4.  – логическая функция двух переменных A и B.

Значения логической функции для разных сочетаний значений входных переменных – или, как это иначе называют, наборов входных переменных – обычно задаются специальной таблицей. Такая таблица называется таблицей истинности.

Приведем таблицу истинности основных логических операций (таблица 1.2) Таблица 1.2

1.  Определить количество строк: 

    На входе два простых высказывания: А и В, поэтому n=2 и количество строк =2²+1=5.

2.  Определить количество столбцов:

    Выражение состоит из двух простых выражений (A и B) и двух логических операций (1 инверсия, 1 конъюнкция), т.е. количество столбцов таблицы истинности = 4.

3.  Заполнить столбцы с учетом таблиц истинности логических операций (таблица 1.3). Таблица 1.3. Таблица истинности для логической операции

Логические формулы можно также представлять с помощью языка логических схем. 

Существует три базовых логических элемента, которые реализуют три основные логические операции :

    логический элемент «И» – логическое умножение – конъюнктор;        логический элемент «ИЛИ» – логическое сложение – дизъюнктор;        логический элемент «НЕ» – инверсию – инвертор.

3.1.Алгоритм построения логических схем.

1.    Определить число логических переменных.

2.    Определить количество логических операций и их порядок.

3.    Изобразить для каждой логической операции соответствующий ей логический элемент.

4.    Соединить логические элементы в порядке выполнения логических операций.

Пример 6. По заданной логической функции  построить логическую схему.

1.    Число логических переменных = 2 (A и B).

2.    Количество операций = 5 (2 инверсии, 2 конъюнкции, 1 дизъюнкция). Сначала выполняются операции инверсии, затем конъюнкции, в последнюю очередь операция дизъюнкции.

3.    Схема будет содержать 2 инвертора, 2 конъюнктора и 1 дизъюнктор.

4.    Построение надо начинать с логической операции, которая должна выполняться последней. В данном случае такой операцией является логическое сложение, следовательно, на выходе должен быть дизъюнктор. На него сигналы подаются с двух конъюнкторов, на которые, в свою очередь, подаются один входной сигнал нормальный и один инвертированный (с инверторов).

3.2. Логические законы и правила преобразования логических выражений

Если две формулы А и В одновременно, то есть при одинаковых наборах значений входящих в них переменных, принимают одинаковые значения, то они называются равносильными.

В алгебре логики имеется ряд законов, позволяющих производить равносильные преобразования логических выражений.

1.  Закон двойного отрицания: ;

2.  Переместительный (коммутативный) закон:

 для логического сложения:           ;  для логического умножения:   ;

3. Сочетательный (ассоциативный) закон:

•     для логического сложения:

•     для логического умножения:      ;

4. Распределительный (дистрибутивный) закон:

•     для логического сложения:  ;

•     для логического умножения:

5. Законы де Моргана:

 для логического сложения:  ;  для логического умножения:  ;

6. Закон идемпотентности:

 для логического сложения:           ;  для логического умножения:      ;

7. Законы исключения констант:

•     для логического сложения:

•     для логического умножения:     ;

8. Закон противоречия:        ; 9. Закон исключения третьего:         ; 10. Закон поглощения:

•     для логического сложения: ;

•     для логического умножения:

11.  Правило исключения импликации:

12.  Правило исключения эквиваленции: .

Справедливость этих законов можно доказать составив таблицу истинности выражений в правой и левой части и сравнив соответствующие значения.

Основываясь на законах, можно выполнять упрощение сложных логических выражений. Такой процесс замены сложной логической функции более простой, но равносильной ей, называется минимизацией функции. Пример 7. Упростить логическое выражение Согласно закону де Моргана:

Согласно сочетательному закону:                                                                                         .

Согласно             закону             противоречия             и             закону             идемпотентности:

/

Практическая работа № 3

Цель работы: освоить алгоритм построения таблиц истинности для логических функций; научиться определять и анализировать функции проводимости переключательных схем. Задания  

Вариант 1 

1.  Составить таблицу истинности логического выражения         

2.  Построить логическую схему функции

3.  Упростить логическое выражение

4.  Определить, являются ли два высказывания эквивалентными A & ¬(¬B v C) и A & B & ¬C 5. Определить истинность или ложность высказываний (¬(X<5) v (X<3)) & (¬(X<2) v (X<1)) при X=1

Вариант 2 

1.  Составить таблицу истинности логического выражения        

2.  Построить логическую схему функции

3.  Упростить логическое выражение

4.  Определить, являются ли два высказывания эквивалентными ¬(¬A & B v A & (B v ¬C)) и ¬B & (¬A v C)

5.  Определить истинность или ложность высказываний (¬(X<5) v (X<3)) & (¬(X<2) v (X<1) при X=3

Вариант 3 

1.   Составить таблицу истинности логического выражения        

2.   Построить логическую схему функции

3.   Упростить логическое выражение

4.   Определить, являются ли два высказывания эквивалентными ¬C v ¬B v ¬(A v ¬C) и ¬A &

B v ¬C & B

5. Определить истинность или ложность высказываний X>1 & (¬(X<5) v (X<3)) при X=2

Вариант 4 

1.   Составить таблицу истинности логического выражения        

2.   Построить логическую схему функции

3.   Упростить логическое выражение  

4.   Определить, являются ли два высказывания эквивалентными ¬(А v ¬В) v ¬B & C и ¬A &

(B  C)

5. Определить истинность или ложность высказываний ¬((X>2) v (X<2)) v (X>4) при X=1

Вариант 5 

1.  Составить таблицу истинности логического выражения       .

2.  Построить логическую схему функции 

3.  Упростить логическое выражение

4.  Определить, являются ли два высказывания эквивалентными

5.  Определить истинность или ложность высказываний X>1 & (¬(X<5) v (X<3)) при X=2

Дополнительные задания В соответствии с выбранным заданием выполнить:

1.   составить таблицу истинности логического выражения

2.   построить логическую функцию по таблице истинности

3.   по таблице истинности построить логическую функцию с помощью СДНФ и минимизировать

4.   построить логическую  схему

a)    А Ú  (¬B Ù C) .

b)   ¬ (А Ú  B) Ù (A Ù ¬ B) .

c)    (А Ú  B) Ú  (C Ù B) .

Контрольные вопросы:

1.    Что такое высказывание (приведите пример)? 

2.    Что такое составное высказывание (приведите пример)? 

3.    Укажите приоритеты выполнения логических операций.

4.    Составьте таблицу истинности для следующих операций: отрицание, конъюнкция, дизъюнкция, импликация, эквиваленция.

5.    Изобразите функциональные элементы: конъюнктор, дизъюнктор, инвертор.

6.    Какие логические выражения называются равносильными?

7.    Запишите основные законы алгебры логики.

Литература

1.    Учебно-тренировочные материалы для подготовки к единому государственному экзамену. Информатика/ Крылов С.С., Лещинер В.Р., Супрун П.Г., Якушкин П.А.; под ред. Лещинера В.Р. – М. Интеллект-Центр, 2005 – 136 с.

2.    Информатика и информационные технологии. Учебник для 10-11 классов/ Н.Д. Угринович Н.Д. – М.: Бином. Лаборатория знаний, 2003. – 512 с.: ил.

3.    Информатика. 7-8 класс/ Под ред. Н. В. Макаровой. – СПб: Издательство «Питер», 2000. – 368с.: ил.

4.    Информатика: Учеб. Пособие для 10-11 кл. общеобразоват. Учреждений/ Л. З. Шауцукова. – 3-е изд. – М.: Просвещение, 2003. – 416 с.: ил.

5.    Босова Л.Л.,Босова А.Ю. // Информатика и ИКТ: учебник 9 класс, М.: БИНОМ. Лаборатория знаний, 2012. -244 с.

6.    Казиев В.М. // Информатика в примерах и задачах - Москва “Просвещение” 2007. -304 с.