РАЗДЕЛ

ПАРНАЯ РЕГРЕССИЯ И КОРРЕЛЯЦИЯ

1 Л. МЕТОДИЧЕСКИЕ УКАЗАНИЯ

Парная регрессия — уравнение связи двух переменных у и х:

где у — зависимая переменная (результативный признак); х — независимая, объясняющая переменная (признак-фактор).

         Различают линейные и нелинейные регрессии.             

Линейная регрессия: у = а + Ь • х + Е.

Нелинейные регрессии делятся на два класса: регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, и регрессии, нели- нейные по оцениваемым параметрам.

Регрессии, нелинейные по объясняющим переменным:

•      полиномы разных степеней у =a+bl • х + b2 • х ² +b3 • х ^з +8;

•      равносторонняя гипербола у = а + — + е.

х

Регрессии, нелинейные по оцениваемым параметрам:

•      степенная  •е;

•      показательная у = а.» • е; а+Ьх

•      экспоненциальная у = е

Построение уравнения регрессии сводится к оценке ее параметров. Для оценки параметров регрессий, линейных по параметрам, используют метоД наименьших кваДратов (МНЮ. МНК позволяет получить такие (Щени параметров, при которых сумма квадратов отклонений фактических значений результативного признака у от теоретических минимальна, т.е.

5

Для линейных и нелинейных уравнений, приводимых к линейным, решается следующая система относительно а и Ь:

=Еух.

Можно воспользоваться готовыми формулами, которые вытекают из этой системы:

cov(x,y) _ у, х— у •i

                                                                                                                                   2                                   —2

Тесноту связи изучаемых явлений оценивает линейный коэффичиент парной корреляции rxy для линейной регрессии (—l < rxy < 1):

                                               б     cov(x,y) _ ух— Г • 7

                                                   rxy =            =

                                                  6х6 у           6х0у

и инДекс корреляции р», — для нелинейной регрессии (0 Spxy S 1):

Рху

 Оценку качества построенной модели даст коэффициент (индекс) детерминации, а также средняя ошибка аппроксимации.

Средняя ошибка аппроксимации — среднее отклонение расчетных значений от фактических:

Допустимый предел значений А — не более 8 — 1094.

СреДний коэффициент эластичности Э показывает, на сколько

процентов в среднем по совокупности изменится результат у от своей средней величины при изменении фактора х на 1 ⁰/0 от своего среднеш значения:

Задача Дисперсионного анализа состоит в анализе дисперсии зависимой переменной:

цу -у) ² = цјх -у) ² +Цу-јх) ² ,

Долю дисперсии, объясняемую регрессией, в общей дисперсии результативного признака у характеризует коэффициент (инДекс) Детерминации R .

2            _ цјх -у) цу-у)2

Коэффициент детерминации — квадрат коэффициента или индекса корреляции.

F-mecm — оценивание качества уравнения регрессии — состоит в проверке гипотезы Но о статистической незначимости уравнения регрессии и показателя тесноты СВЯЗИ. Для этого выполняется сравнение фактического и критического (табличного) зна- чений Е-критерия Фишера. определяется из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:

Ефакт =

где п — число единиц совокупности; т — число параметров при переменных х.

 — это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы и уровне значимости а. Уровень значимости а — вероятность отвергнуть правильную гипотезу при условии, что она верна. Обычно а принимается равной 0,05 или 0,01.

Если < , то Но — гипотеза о случайной природе оцениваемых характеристик отклоняется и признается их статистическая значимость и надежность. Если > то гипотеза Но не отклоняется и признается статистическая незначимость, ненадежность уравнения регрессии.

7

Для ОЦеНКИ статистической значимости коэффициентов регрессии и корреляции рассчитываются г-критерий СтьюДента и доверительные интервалы каждого из показателей. Выдвигается гипотеза Но о случайной природе показателей, т.е. о незначимом их отличии от нуля. Оценка значимости коэффициентов регрессии и корреляции с помощью г-критерия Стьюдента проводится путем сопоставления их значений с величиной случайной ошибки:

а

а

Случайные ошибки параметров линейной регрессии и коэффициента корреляции определяются по формулам:

ост

по х

rxy

Сравнивая фактическое и критическое (табличное) значения т-статистики — и — принимаем или отвергаем гипотезу Но.

Связь между Е-критерием Фишера и т-статистикой Стьюдента выражается равенством

Если < Тфакт, то Но отклоняется, т.е. а, Ь и г». не случайно отличаются от нуля и сформировались под влиянием систематически действующего фактора х. Если > Тфит, то гипотеза Но не отклоняется и признается случайная природа формирования а, Ь или rxy.

Для расчета доверительного интервала определяем предельную ошибку д для каждого показателя:

                                                      Да = ГтаблТа              Дь = ГтаблТЬ•

Формулы для расчета Доверительных интералов имеют следующий вид:

Уа               = а— Да min         тах    min          тах

Если в границы доверительного интервала попадает ноль, т.е. нижняя граница отрицательна, а верхняя положительна, то оцениваемый параметр принимается нулевым, так как он не может одновременно принимать и положительное, и отрицательное значения.

Прогнозное значение ур определяется путем подстановки в уравнение регрессии ух = а + Ь. х соответствующего (прогнозного) значения хр. Вычисляется среДняя станДартная ошибка прогноза

где б         

и строится Доверительный интервал прогноза:

                 min           тах

где Д ^А

1.2. РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ

Пример 1

По семи территориям Уральского района за 199X г. известны значения двух признаков (табл. 1.1).

Таблица 1.1

Требуется.

1.                    Для характеристики зависимости у от х рассчитать параметры следующих функций:

а) линейной;

б) степенной;

в) показательной;

г) равносторонней гиперболы.

2.                    Оценить каждую модель через среднюю ошибку аппроксимации А и Е-критерий Фишера.

Решение

1а. Для расчета параметров а и Ь лине й ной регрессии y=a+b• х решаем систему нормальных уравнений относительно а и Ь:

                 По исходным данным рассчитываем Бу, Ъ, Еух, 2х² , ЕВ.        

Таблица 1 .2

3166,05 - 57,89 • 54,9

 —0,35,

5,862

Уравнение регрессии: = 76,88 — 0,35 • х. С увеличением среднедневной заработной платы на руб. доля расходов на покупку продовольственных товаров снижается в среднем на 0,35 %-ных пункта. Рассчитаем линейный коэффициент парной корреляции:

—0,35       = -0,357. 5,74

Связь умеренная, обратная.

Определим коэффициент детерминации:

= 0,127.

Вариация результата на 12,7⁰/0 объясняется вариацией фактора х.

Подставляя в уравнение регрессии фактические значения х, определим теоретические (расчетные) значения Л.. Найдем величину средней ошибки аппроксимации А :

56,7.lOWh

7

В среднем расчетные значения отклоняются от фактических на 8,170.

Рассчитаем вкритерий:

0,127 факт —          0,873

            поскольку 1 S           00, следует рассмотреть F

Полученное значение указывает на необходимость принять гипотезу Но о случайной природе выявленной зависимости и статистической незначимости параметров уравнения и показателя тесноты связи.

16. Построению степ ен ной модели у = а • х ^ь предшествует процедура линеаризации переменных. В примере линеаризация производится путем логарифмирования обеих частей уравнения:

У=С+Ь.Х, где У: lg у, Х = lg х, С = lg а.

Для расчетов используем данные табл. 1 3

Таблица 1.3

Рассчитаем С и Ь:

У.Х-Г.Х 3,0572 1,7605 • 1,7370

 —0,298;

                                      ох                           0,04842

С = 2,278.

Получим линейное уравнение: = 2,278—0,298, Х.

Выполнив его потенцирование, получим: 9=102,278 -0,298 = 189,7.х—0,298

Подставляя в данное уравнение фактические значения х, получаем теоретические значения результата . По ним рассчитаем показатели: тесноты связн — индекс корреляции р ху и среднюю ошибку аппроксимации А, :

                                       рху —= 0,3758,                                     7 = 8,070.

Характеристики степенной модели указывают, что она несколько лучше линейной функции описывает взаимосвязь. 1в. Построению уравнения пок аз ател ь ной кривой предшествует процедура линеаризации переменных при логарифмировании обеих частей уравнения:

lgy= lga+x•lgb;

                                            У=С+В.х,   

Для расчетов используем данные табл. 1.4.

Таблица 1.4

Значения параметров регрессии А и В составили:

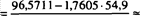Y.x-Y .i

—0,0023, 02х     5,862

А = У - В.? = = 1,887.

л

Получено линейное уравнение: У = 1,887 -- 0,0023- х.

Произведем потенцирование полученного уравнения и запишем его в обычной форме:

1,887 10-0,0023х = 77,1 • 0,9947 ^Х .

Тесноту связи оценим через индекс корреляции рху . р ху-= 0,3589.

Связь умеренная.

А = 8,070 , что говорит о повышенной ошибке аппроксимации, но в допустимых пределах. Показательная функция чуть хуже, чем степенная, она описывает изучаемую зависимость.

1г. Уравнение равносторонней гиперболы y=a+b•—

линеаризуется при замене: = — . Тогда у——a+b•z.

х

Для расчетов используем данные табл. 1.5.

Таблица 1.5

Значения параметров регрессии а и Ь составили:

= 38,5;

1051,4.

Получено уравнение: = 38,5+ 1051,4 — х

Индекс корреляции: рху —= 0,3944.

А = 8,170 . По уравнению равносторонней гиперболы получена наибольшая оценка тесноты связи: р ху = 0,3944 (по сравнению с

линейной, степенной и показательной регрессиями). А остается на допустимом уровне:

n-m-1 0,1555

2.                                                                            факт• 5 = 0,92, 0,8445

где          -6,6 >           а = 0,05.

Следовательно, принимается гипотеза Но о статистически незначимых параметрах этого уравнения. Этот результат можно объясннть сравнительно невысокой теснотой выявленной зависнмости и небольшнм числом наблюдений.

Пример 2

По территориям региона приводятся данные за 199Х г. (табл. 1.6).

Требуется

1.   Построить линейное уравнение парной регрессии у от х.

2.   Рассчитать линейный коэффициент парной корреляции и среднюю ошибку аппроксимации.

З. Оценить статистическую значимость параметров регрессии и корреляции.