
ПОТЕРИ ПРЕДВАРИТЕЛЬНОГО НАПРЯЖЕНИЯ ОТ УСАДКИ И НЕЛИНЕЙНОЙ ПОЛЗУЧЕСТИ БЕТОНА ЖЕЛЕЗОБЕТОННЫХ СТЕРЖНЕВЫХ СИСТЕМ
Тошматов Улугбек
Ферганский политехнический институт,
г. Фергана, Республика Узбекистан
LOSSES OF PRESTRESS FROM SHRINKAGE AND NON-LINEAR CREEP OF CONCRETE OF REINFORCED CONCRETE ROD SYSTEMS
Toshmatov Ulugʻbek
Fergana Polytechnic Institute, Fergana city, UZBEKISTAN
Аннотация: в статье ппредставлен алгоритм расчета предварительно-напряженных железобетонных стержневых систем с учетом потери преднапряжения от нелинейной работы железобетона с течением времени
Ключевые слова: напрежение, преднапрежение, деформация, ползучесть, усадка.
Abstract: An algorithm for calculating prestressed reinforced concrete rod systems is presented taking into account the loss of prestress from non-linear operation of reinforced concrete over time.
Key words: stress, prestress, deformation, creep, shrinkage.
Введения. Предварительно напряженные железобетонные конструкции имеют сложное напряженное состояние, изменяющееся во времени от воздействия внешних нагрузок, проявления неупругих деформаций бетона, релаксации напряжений в стали и других условиях. В связи с этим, при проектировании предварительно напряженных конструкций необходимо знать основные причины, влияние на характер и величину изменения напряжений в арматуре и бетоне на различных стадиях их работы.
Модели образцов и методика исследований. Точный учет факторов, влияющих на величину потерь, как правило, представляет сложную и нередко трудно решаемую задачу [1,2,3]. В связи с этим, для практических расчетов приходится принимать менее точные, но упрощенные способы учета потерь предварительного напряжения.
Потери предварительного напряжения, учитываемые в расчетах, могут быть подразделены на следующие виды: усадка бетона; ползучесть бетона; релаксация напряжений в арматуре; деформация анкеров, шайб и прокладок; деформация швов между блоками составных конструкций; деформация форм для изготовления конструкций; трения арматуры в стенке канала или поверхности бетона конструкций; смятие бетона под витками кольцевой (спиральной) арматуры; разность температуры натянутой арматуры и температура устройств, воспринимающих усилие напряжения; многократно повторяющаяся нагрузка; разность коэффициентов линейного удлинения арматуры и бетона при работе конструкции в условиях повышенной температуры. Вышеуказанные факторы, влияющие на потери предварительного напряжения от усадки и ползучести бетона, релаксация напряжений стали проявляются в течении длительного времени.
В эксплуатационной стадии на потери предварительного напряжения действуют основные усадки и ползучесть бетона. Определим потери предварительного напряжения от ползучести бетона по формуле [4].
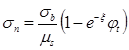 (1)
(1)
где: 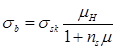 (2)
- начальное
напряжение.
(2)
- начальное
напряжение.
С учетом роста модуля упругой деформации бетона во времени опытные параметры определяются:
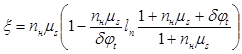 (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
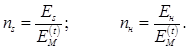 (6)
(6)
![]() (7)
(7)
![]() -
предельная характеристика ползучести;
-
предельная характеристика ползучести; ![]() -
значение предельной характеристики ползучести для средних условий;
-
значение предельной характеристики ползучести для средних условий; ![]() - поправочный коэффициент,
зависящий от влажности среды, в которой находится элемент (конструкция).
- поправочный коэффициент,
зависящий от влажности среды, в которой находится элемент (конструкция).
![]() - поправочный коэффициент,
учитывающий масштабный факторы (размеры элемента).
- поправочный коэффициент,
учитывающий масштабный факторы (размеры элемента). ![]() -
поправочный коэффициент, зависящий от возраста бетона
-
поправочный коэффициент, зависящий от возраста бетона ![]() d
момент загружения элемента
d
момент загружения элемента ![]() –
упруго-мгновенные деформации бетона;
–
упруго-мгновенные деформации бетона; ![]() -
константы, зависящие от условий твердения и состава бетона [5,6].
-
константы, зависящие от условий твердения и состава бетона [5,6].
Потери предварительного напряжения от усадки бетона определяются по формуле:
![]() (8)
(8)
где:
![]() -
предельная относительная деформация усадки;
-
предельная относительная деформация усадки;
![]() -
значение предельной относительной деформации усадки для средних условий;
-
значение предельной относительной деформации усадки для средних условий;
![]() -
поправочный коэффициент, зависящий от времени
-
поправочный коэффициент, зависящий от времени ![]() ,
с которого начинается учет усадки и бетона.
,
с которого начинается учет усадки и бетона.
Определения потери предварительного напряжения от ползучести и усадки во времени, находим величину «сжимающей силы».
![]() (9)
(9)
Вычисленный ![]() рассматривается
как внешняя нагрузка и прилагается к концу пред напряжённых стержней с обратным
знаком.
рассматривается
как внешняя нагрузка и прилагается к концу пред напряжённых стержней с обратным
знаком.
Результаты экспериментов и их анализ. По разработанным алгоритмам составлена программа и рассмотрены примеры.
Программа предназначена для расчета предварительно напряженных железобетонных ферм с учетом жесткости узлов, ползучести и усадки бетона, а также для изменения пред- напряжения во времени, находящийся под действием внешних нагрузок, с использованием метода последовательных приближений.
Общая структура процесса расчета программы приведена на рис (1).
Результаты рассмотренных примеров (расчет предварительно напряженных железобетонных ферм с учетом жесткости узлов в неупругой стадии) показывают, что напряжения от усадки и ползучести в большинстве элементов существенно не изменяются и лишь в нижних поясах значительно уменьшается [7,8,9].
На основе графиков (рис. 2, 3, 4) приращение ∆σ при различных процентах армирования полученных согласно табл.1 показывает, что от действия постоянных эксплуатационных нагрузок напряжения в стержнях фермы во времени в верхнем поясе уменьшается, а в нижнем поясе, раскосе и стойке увеличивается.
При увеличении процента армирования приращения напряжений - ∆σ изменяется в следующих пределах:
а) в нижнем поясе от 2 до 8%; б) в верхнем поясе от 0,5 до 3,5%; в) в раскосах от 0,2 до 2,4%.
При одном и том же уровне нагрузки с увеличением процента армирования процесс перераспределения усилий растет.
Это обусловлено тем, что в элементах фермы с высоким процентом армирования в сжатом бетоне и следовательно нелинейность деформирования растет.
Нелинейность деформирования способствует перераспределению напряжений между стержнями фермы.
|
Ввод
исходных информаций Вычисление
упруга-мгновенных модулей деформации бетона |
Определение
напряжений в сжатом бетоне Определение
временного модуля деформации бетона |
||||||||
|
Вычисление
жесткости сечения |
Проверка
условия |
||||||||
|
Определение
внутренних усилий в стержнях фермы |
Проверка
условия |
||||||||
|
Вычисление
угловых перемещений стержней фермы |
Проверка
условия |
||||||||
|
Определение
угловых перемещений узлов фермы |
Вычисление
интегрального модуля деформации бетона |
||||||||
|
Вычисление
жесткости арматуры Вычисление
напряжения |
Определение
напряжения в растянутой арматуре |
||||||||
|
|
Определение
потери предварительного напряжения |
||||||||
|
Вычисление
приведенного момента инерции сжатой зоны бетона Вычисление
приведенной площади бетона сжатой зоны |
Проверка
условия |
||||||||
|
|
Проверка
условия |
||||||||
|
Проверка
условия |
Вывод
результатов расчета на печать |
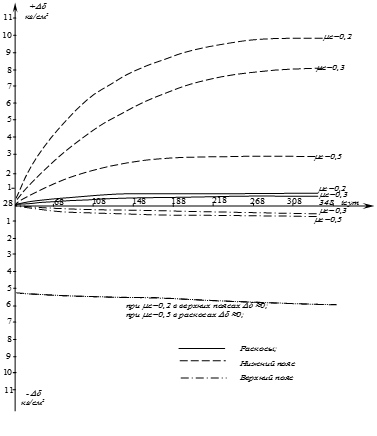
Рис.2. Приращение напряжений Dd при увеличений mс в сжатых элементах.
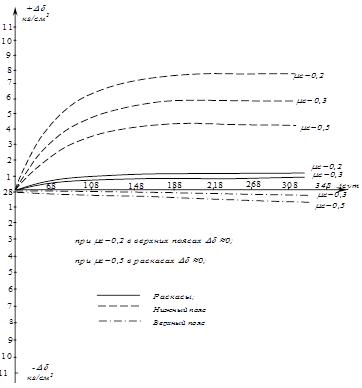
Рис.3. Приращение напряжений Dd при увеличений mс в растянутых элементах.
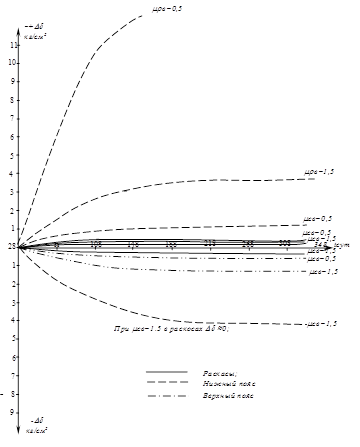
Рис.4. Приращение напряжений Dd при увеличении mа соответственно во всех элементах
Таблица 1.
|
Элементы фермы |
Постановка задачи: t сутки |
% армирования |
||||||||
|
0,2с |
0,5с |
0,5р |
2,5р |
0,5св |
1,5св |
0,5рв |
1,5рв |
|||
|
Верх-ний пояс |
Упругая, нелинейная неравновесная, |
tо=28 tо=28 t=112 |
1,000 0,950 0,947 |
1,000 0,892 0,887 |
1,000 0,954 0,951 |
1,000 0,970 0,964 |
1,000 0,917 0,911 |
1,000 0,706 0,696 |
1,000 1,007 1,006 |
1,000 0,927 0,926 |
|
Ниж-ний пояс |
Упругая, нелинейная неравновесная, |
tо=28 tо=28 t=112 |
1,000 1,205 1,214 |
1,000 1,058 1,058 |
1,000 1,135 1,137 |
1,000 1,139 1,151 |
1,000 1,016 1,024 |
1,000 0,666 0,669 |
1,000 1,217 1,223 |
1,000 1,089 1,093 |
|
Рас-косы |
Упругая, нелинейная неравновесная, |
tо=28 tо=28 t=112 |
1,000 0,658 0,660 |
1,000 0,418 0,420 |
1,000 0,667 0,670 |
1,000 0,649 0,650 |
1,000 0,409 0,410 |
1,000 0,152 0,152 |
1,000 1,328 1,386 |
1,000 0,493 0,494 |
Примечание: с, р, св, рв означают, что проценты армирования изменяются только в сжатых, растянутых и соответственно во всех элементах фермы.
Список литературы:
[1]. Бондаренко В.М. «Некоторые вопросы нелинейной теории ползучести бетона». Харьков, изд-во Харьковского университета: 1991. Стр. 56.
[2]. Abdukhalimjohnovna M. U. Failure Mechanism Of Bending Reinforced Concrete Elements Under The Action Of Transverse Forces //The American Journal of Applied sciences. – 2020. – Т. 2. – №. 12. – С. 36-43.
[3]. Abdukhalimjohnovna M. U. Technology Of Elimination Damage And Deformation In Construction Structures //The American Journal of Applied sciences. – 2021. – Т. 3. – №. 05. – С. 224-228.
[4]. Мирзаахмедов А. Т., Мирзаахмедова У. А., Максумова С. Р. Алгоритм расчета предварительно напряженной железобетонной фермы с учетом нелинейной работы железобетона //Актуальная наука. – 2019. – №. 9. – С. 15-19.
[5]. Mirzaakhmedova U. A. Inspection of concrete in reinforced concrete elements //Asian Journal of Multidimensional Research. – 2021. – Т. 10. – №. 9. – С. 621-628.
[6]. Mirzaakhmedov A. T., Mirzaakhmedova U. A. Prestressed losses from shrinkage and nonlinear creep of concrete of reinforced concrete rod systems //EPRA International journal of research and development (IJRD). – 2020. – Т. 5. – №. 5. – С. 588-593.
[7]. Mirzaakhmedov A. T., Mirzaakhmedova U. A. Algorithm of calculation of ferro-concrete beams of rectangular cross-section with one-sided compressed shelf //Problems of modern science and education. Scientific and methodical journal.–2019. – 2019. – Т. 12. – С. 145.
[8]. Мирзаахмедов А. Т., Мирзаахмедова У. А. Алгоритм расчета железобетонных балок прямоугольного сечения с односторонней сжатой полкой //Проблемы современной науки и образования. – 2019. – №. 12-2 (145). – С. 50-56.
[9]. Мирзаахмедов, А. Т. (2022). Оптимального Проектирования Стержневых Систем С Учётом Нелинейной Работы Железобетона. CENTRAL ASIAN JOURNAL OF THEORETICAL & APPLIED SCIENCES, 3(4), 64-69.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.