Практическая работа по информатике

Практическая работа №12

Тема: Логика. Основные логические конструкции и их описание.

Цель занятия: Изучить основные логические конструкции и их описание

Необходимое оборудование: сеть Интернет, ПК.

деятельности, формализуемых с помощью логического языка. Поскольку это знание получено разумом, логика также определяется как наука о формах и законах правильного мышления. Так как мышление оформляется в языке в виде рассуждения, частными случаями которого являются доказательство и опровержение, логика иногда определяется как наука о способах рассуждения или наука о способах доказательств и опровержений.

Логика как наука изучает методы достижения истины в процессе познания опосредованным путём, не из чувственного опыта, а из знаний, полученных ранее, поэтому её также можно определить как науку о способах получения выводного знания.

Одна из главных задач логики – определить, как прийти к выводу из предпосылок (правильное рассуждение) и получить истинное знание о предмете размышления, чтобы глубже

разобраться в нюансах изучаемого предмета мысли и его соотношениях с другими аспектами рассматриваемого явления.

В    любой науке логика служит одним из основных инструментов. Кроме философии, логика также является подразделом математики, а булева алгебра одной из основ информатики.

Математическая логика (теоретическая логика, символическая логика) раздел математики, изучающий математические обозначения, формальные системы, доказуемость математических суждений, природу математического доказательства в целом, вычислимость и прочие аспекты оснований математики. В более широком смысле рассматривается как математизированная ветвь формальной логики – «логика по предмету, математика по методу», «логика, развиваемая с помощью математических методов»

Алгебра логики (алгебра высказываний) — раздел математической логики, в котором изучаются логические операции над высказываниями. Чаще всего предполагается, что высказывания могут быть только истинными или ложными, то есть используется так называемая бинарная или двоичная логика, в отличие от, например, троичной логики. Базовыми элементами, которыми оперирует алгебра логики, являются высказывания.

Высказывания строятся над множеством, элементами которого определены три операции: отрицание (унарная операция ¬),

конъюнкция (сложение Ù ), дизъюнкция (умножение Ú),

. Также вводятся дополнительные операции, такие как эквиваленция («тогда и только тогда, когда» «), импликация («следовательно» ®), логический ноль 0 и логическая единица 1 — константы.

Так же используются названия

·       Дизъюнкция — пропозициональная формула, являющаяся дизъюнкцией одного или более литералов.

· Конъюнкция — пропозициональная формула, являющаяся конъюнкцией одного или Простейший и наиболее широко применяемый пример такой алгебраической системы строится

с  использованием множества B, состоящего всего из двух элементов: B = { Ложь, Истина }

Как правило, в математических выражениях Ложь отождествляется с логическим нулём,

а  Истина — с логической единицей, а операции отрицания (НЕ ¬), конъюнкции (И Ù) и дизъюнкции (ИЛИ Ú) определяются в привычном нам понимании. Легко показать, что на данном множестве B можно задать четыре унарные и шестнадцать бинарных отношений и все они могут быть получены через суперпозицию трёх выбранных операций.

Опираясь на этот математический инструментарий, логика высказываний изучает высказывания и предикаты

Логика высказываний послужила основным математическим инструментом при создании компьютеров. Она легко преобразуется в битовую логику: истинность высказывания обозначается одним битом (0 — ЛОЖЬ, 1 — ИСТИНА); тогда операция приобретает смысл вычитания из единицы; немодульного сложения &(Ù) ; умножения *(Ú). Впоследствии булева алгебра была обобщена от логики высказываний путём введения характерных для логики высказываний.

Решение задач по основам логики основывается на таблице истинности. Таблица истинности — это таблица, описывающая логическую функцию.

Практическая часть

Задание 1. Построить таблицу истинности выражения F = ¬AÙ¬B

Задание 3. Построим таблицу истинности F = (¬AÚB)® ( AÚB)

Задание 4. Построим таблицу истинности F = AÚBÚС

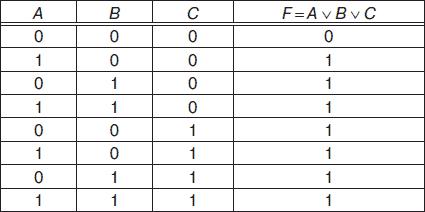
Задание 5. Постройте самостоятельно таблицу истинности

1). F= (AÙB)Ú(ØAÙØB

2). F= Ø (AÙB)ÚØ(AÙB)

3). F= (AÚB)Ú(ØAÙØB),

4). F= (AÙØB)ÚØ(AÙB),

5). F= (AÙB)^(ØAÚØB),

6). F= Ø AÚBÚØ(AÙB).

Контрольные вопросы

1)      Что такое логика?

2)      Что изучает логика?

3)      Задачи логики

4)      Что изучает математическая логика?

5)      Что такое алгебра логики?

6)      Элементы алгебры логики

7)      Операции высказываний

8)      Что такое дизъюнкция, как записывается?

9)      Что такое конъюнкция, как записывается?

10)  Что такое отрицание, как записывается?

11)  Что такое эквиваленция, как записывается?

12)  Что такое импликация, как записывается?