Практическая работа по теме: «Отношение длины окружности к её диаметру»

6 класс                                               

Практическая работа «Отношение длины окружности к её диаметру»

Цель работы: измерить длину окружности, проверить достоверность числа π.

Оборудование: циркуль, линейка, карандаш, предметы цилиндрической формы, нитка (сантиметровая лента).

Повторите:

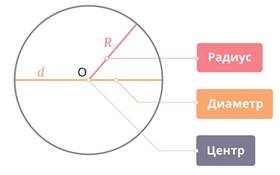
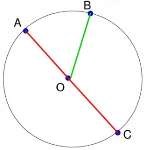
О – центр окружности,

АО = ВО = СО = r – радиус окружности,

АС = d – диаметр окружности.

d = 2r

Окружность – это множество всех точек, находящихся на одинаковом расстоянии от заданной точки, которая называется центром окружности.

Элементы окружности: центр, радиус, диаметр.

Отрезок, соединяющий две точки окружности, называется хордой.

Диаметр – это хорда, проходящая через центр окружности.

Ещё в древности было установлено, что какой бы ни была окружность, отношение её длины к её диаметру является постоянным числом. Сейчас это число обозначают греческой буквой π. (читается – «пи»)

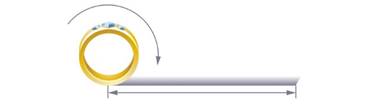
Как измерить дину окружности?

Можно взять сантиметровую ленту (если нет ленты, можно воспользоваться нитью или полоской бумаги).

Можно прокатить кольцо по ровной поверхности, сделав полный оборот.

Обозначим длину окружности буквой С, а её диаметр – буквой d, и запишем формулу:

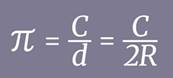
Следовательно, справедливы формулы:

С = πd      или

С = 2πR

С точностью до миллионных π ≈ 3,141593, при округлении до сотых значение   равно 3,14

Круг – это часть плоскости, ограниченная окружностью.

С помощью числа π вычисляют площадь круга.

S = πR²

Запишите

Девятнадцатое декабря

Практическая работа 

Отношение длины окружности к её диаметру

1.     Начертите в тетради таблицу, которую будете заполнять по ходу выполнения практической работы.

2.     Возьмите предмет цилиндрической формы (например), поставьте дном на лист бумаги (можно использовать черновик) и карандашом обведите дно.

3.     Проведите диаметр полученной окружности (соедините две точки, лежащие на окружности отрезком, проходящим через центр окружности) и линейкой измерите диаметр, d (см). Запишите длину диаметра окружности в таблицу.

4.     С помощью сантиметровой ленты или нитки и линейки измерить длину полученной окружности, c (см). Результаты измерений запишите в таблицу.

5.    Вычислите отношение длины окружности к ее диаметру по формуле  и результат вычислений запишите в виде десятичной дроби в таблицу.

6.     Повторить все проделанные действия ещё с двумя предметами цилиндрической формы, но с размерами, которые отличаются от размеров стакана.

7.     Все вычисления должны быть записаны:

1)

2)

3)            

8.     Запишите вывод. (Во сколько раз длина окружности больше диаметра?)

9.