Практическое занятие №6 Методы формирования решений. Функции полезности

Практическое занятие №6 Методы формирования решений. Функции полезности

Методы формирования решений создаются в соответствии с классом задач принятия решений. Данное понятие является многоуровневым и включает в себя сочетания базовых и специфических методов решения задач. Базовые методы используются в различных областях управленческой деятельности, специфические — в некоторых.

К базовым методам относят следующие: .

 целевое управление;

« сетевое планирование и управление; .

статистические методы (временные ряды, уравнения регрессии, прогнозирование и т.д.);

•    методы оптимизации (линейные, нелинейные); . факторный анализ;

•    имитационное моделирование;

•    таблицы решений;

•    нечеткие множества;

•    математический анализ и т.д.

К специфическим методам решения относятся:

•    управление проектами;

•    управление перевозками; « управление запасами;

•    управление цехом и т.д.

Метод формирования решений, как правило, включает в себя один-два базовых и несколько специфических методов решения задач. Устойчивое, широко применяемое сочетание методов решения задач может приобретать имя и тогда оно получает свой собственный статус. Например, сочетание сетевого планирования и управления с методами оптимизации и методами управления перевозками получило название «оперативный анализ и управление перевозками».

Формирование решений осуществляется, как правило, на основе здравого смысла, предполагающего получение определенной выгоды. Для оценки альтернатив разработана теория полезности, которая базируется на нескольких аксиомах. На их основе выведена формула для расчета среднего результата, который будет получен после принятия решения. Формула имеет вид:

R = px + (l-p)y,

гдее   R - математическое ожидание результата принятия решения;

       р - вероятность появления результата х;

        х, у - альтернативы принятия решения.

Пусть существует несколько альтернатив решения.

A = {a_i };  i =  ,

Следствия зависят от внешних факторов и находятся вне контроля:

Q = {q_j };  y =  ,

Вибирая альтернативу a_i для внешнего фактора q_j  получим последствие С_ij

Пускай известно:

а) вероятности влияния внешних факторов  (P(q_j  );

б) полезность от альтернативы а_i  при факторе q_j рівна С_ij. Тогда получим

общуюпользу альтернативы:

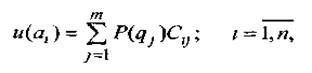
де P(q_j ) — вероятность влияния фактора q_j;

      С_ij —полезность альтернативы  a_i, при влиянии фактора  q_j,

      и (а_i) — общая полезность альтернативы а_i

Полученные результаты можно ранжировать по полезности:

Ψ (a_i, ώ)  ≥ ψ (a_k,  ώ),

 где   ψ — функція ранжирования;

       ώ — вектор оценочных данных, указывающее лицо, которое принимает решение

2.Этапы принятия решений. Критерии оценки, поиск вариантов, выбор

Практика принятия решений многообразна Однако все они реализуются по определенной схеме, подсказываемой здравым смыслом. Для того чтобы принять эффективное решение, необходимо выполнить ряд работ, складывающихся из отдельных этапов, процедур и операций. Среди многочисленных подходов к формированию решений выделим трехэтапную модель Г. Саймона, являющуюся основой для реализации большинства известных на сегодня технологий. Модель приведена на рис. 1

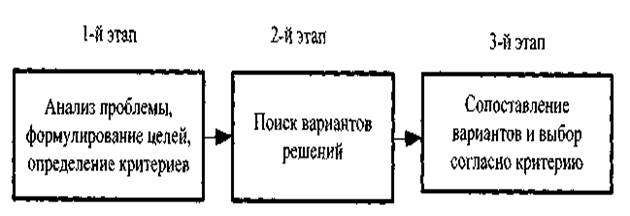
Рис. 1 Трехэтапное формирование решений

Рассмотрим содержание каждого из этапов. На первом этапе применяются в основном неформальные методы для того, чтобы

а) сформулировать проблему;

б) выявить цель;

с) сформулировать критерий оценки принятия решений.

Проблема выражает объективно возникающий в процессе управления вопрос, решение которого диктуется интересами лица, принимающего решение (ЛПР).

Для того чтобы осознать проблему, ЛПР должно дать ответы на ряд вопросов. Например:

1. В чем проблема? Каковы симптомы, т.е. признаки или пока затели проблемы? Что, собственно, не устраивает ЛПР?

2. В чем особенности проблемы? Что мешает или чего не доста ет при наличии проблемы?

3. Можно ли разложить проблему на части, а среди выделенных частей выделить основные и второстепенные проблемы?

Если проблема осознана и идентифицирована количественными показателями или качественными признаками, то далее можно сформулировать цели. Цель — это антипод проблемы. Если проблема это то, чего не хочет ЛПР, то цель — это то, чего он хочет.

В иерархии управления (см. рис. 2.7) формулируются цели, соответствующие своему уровню. На самом высоком уровне находятся цели, носящие директивный характер. Эти цели называют также траекторными. Такое название связано с тем, что заданные цели отражают желаемую траекторию изменения объекта управления во времени. На практике траектория развития предприятия задается с помощью показателей, количественно отражающих уровень достижения той или иной цели.

В процессе управления ЛПР стремится избегать негативных проявлений и добивается совпадения фактической траектории с желаемой. Траекторным целям подчинены рабочие цели, которые меняются в соответствии с возникающей фактической ситуацией.

Директивные цели всегда детализируются. Процесс детализации носит иерархический характер. В результате получают дерево целей. Нижний уровень дерева целей превращается в мероприятие, которое следует выполнить для достижения директивной цели.

Существует следующее правило, согласно которому должно строиться дерево целей:

•    ни одна из нижних вершин дерева не должна входить более, чем в одну верхнюю;

•    вершины дерева одного уровня не должны быть альтернатив ными, т.е. для достижения цели вышестоящего уровня долж ны быть достигнуты все подцели данного уровня;

•    цели нижнего уровня должны являться детализацией цели ближнего верхнего уровня. Если таковой нет, она должна быть введена фиктивно.

Если проблема и цель сформулированы, далее следует разработать критерии, согласно которым выполняется отбор приемлемого решения. Критерием отбора может служить любой признак, значение которого можно зафиксировать в некоторой шкале; Так<как критерий служит для оценки ]вариантов решений, он должен быть измерим. Для этого можно воспользоваться различными шкалами. Распространенными среди них: являются следующие [27]:

•     Шкала наименований используется для присваивания объ ектам наименований или идентификаторов. В этой шкале число может использоваться лишь для обозначения с последующим вы делением объекта из множества других. Например, страницы книги отличаются номерами. Номера страниц не могут быть использованы для каких-либо иных целей, кроме выделения. Нельзя утвер ждать, что материал на с. 20 имеет бльшую ценность, чем материал на с. 25.

•     Ранговая шкала задает отношение порядка. Критерии в этой шкале более информативны по сравнению с предыдущей, так как позволяют манипулировать понятиями «хуже—лучше». Оценки здесь, как правило, балльные, что позволяет их сопоставлять с общепринятыми нормами (например, ранжирование целей по значимости).

•     Шкала интервалов позволяет измерить что-либо в произвольно заданных фиксированных величинах. Примером здесь может служить измерение температур или времени. Температуры по Цельсию и Фаренгейту приводятся к друг другу с помощью линейных преобразований (точка начала отсчета и масштаб, задающий еди ницу измерения).

•     Шкала отношений является дальнейшим развитием шкалы интервалов. Она позволяет сравнивать не только интервалы между собой, но и их отношения. Шкалы отношений используются для из мерения величин, у которых существует естественное начало отсче та (масса, длина, стоимость).

Если известна природа сравниваемых величин, то, как правило, выбор типа шкалы не представляет особых затруднений. Большинство психологических, социальных и других качественных показателей, связанных с учетом человеческого фактора, не могут быть измерены в шкале отношений, а часто и в шкале интервалов, что создает сложности в использовании этих показателей в процессе принятия решения.

Показатели, характеризующие состояние экономического объекта управления, как правило, измеримы в шкале отношений. Если среди показателей выбрать тот, который, по мнению ЛПР, в наибольшей степени характфизует соответствие объекта управления заданному целевому назначению, то он и будет играть роль критерия оценки вариантов решеню • Формировать критерий следует так, чтобы наиболее предпочтительная оценка состояния, объекта или процесса соответствовала его максимуму или минимуму.

Рассмотрим типовые критерии выбора варианта решения. Общее правило для всех критериев можно записать в виде:

Y* = extremum ( β_i, β₂ ..., β_n ),

где Y* — искомый вариант решений;

     β, — коэффициент важности і- го решения.

Эта запись означает, что из множества чисел следует выбрать экстремальное число и по номеру этого числа определить, какое из альтернативных решений является наилучшим.

Если коэффициенты важности определены так, что чем больше их значение, тем лучше решение, то критерий нахождения решения соответствует операции нахождения максимума, т.е.:

Y* = max (β_i, β₂ ..., β_n )

Если коэффициенты важности определены так, что чем меньше их значение, тем более значимо решение, то критерий следующий:

Y* = min (β_i, β₂ ..., β_n )

Приведем три наиболее распространенных критерия, применяемых в области экономики.

Критерий осторожного выбора. Этот критерий соответствует правилу «рассчитывай на худший случай»:

Y* = C_ij

где C_ij — результаты, которые будут получены по і- му варианту в j- й ситуации.

В соответствии с этим критерием последовательно выполняются операции нахождения минимальных значений результатов во всех ситуациях, и затем из полученных вариантов находится тот, что имеет максимальное значение. Его номер и определит наилучшее решение. Такой критерий называют максиминным.

Критерий оптимистичного выбора ориентирован на правило «рассчитывай на лучший случай». Наилучший вариант определяется по формуле:

Y* = C_ij

Критерий максимума среднего выигрыша используется тогда, когда известны вероятности возникновения той или иной ситуации. Если предпочтения измеряются в шкале отношений, то средний выигрыш при каждом варианте рассчитывается так:

М_i =                                                                

где M_t — математическое ожидание выигрыша в случае принятия і- го  решения;

Pj — вероятность появления j- й ситуации;

Сij — оценка /-го решения при j- ой ситуации.

На втором этапе формирования решений происходит поиск различных вариантов — альтернатив. Варианты могут отыскиваться в различных формах и шкалах измерений (действия, состояния, маршруты, стоимости и т.д.).

Варианты, как правило, задаются либо перечислением, если таковых не очень много, либо описанием их свойств. Генерация вариантов решений в большинстве случаев выполняется либо с помощью различного рода аналитических моделей, либо с помощью баз знаний экспертных систем