Презентация "Основы логики. Логические выражения" 10 класс

Основы логики. Основы логики. Логическое Логическое умножение, умножение, сложение и сложение и вычитание. вычитание. Логические Логические выражения выражения Вид урока: лекция Вид урока: лекция Цель: способствовать развитию информационно – Цель: способствовать развитию информационно – коммуникативной самообразовательной коммуникативной самообразовательной компетенции компетенции Задача: ознакомиться с основами алгебры логики Задача: ознакомиться с основами алгебры логики (высказывания, операции и выражения) (высказывания, операции и выражения)

Сколько различных чисел существует?  Сколько различных чисел существует? Сколько различных значений могут  Сколько различных значений могут  принимать переменные?  принимать переменные?  Сколько различных значений могут  Сколько различных значений могут  принимать логические переменные?  принимать логические переменные?  «Истина» (1) «Истина» (1) «Ложь» (0) «Ложь» (0)

Простые высказывания в алгебре логики Простые высказывания в алгебре логики обозначаются прописными латинскими обозначаются прописными латинскими буквами. буквами. А – «Два умножить на два равно А – «Два умножить на два равно В – «Два умножить на два равно В – «Два умножить на два равно Какова истинность высказываний? Какова истинность высказываний? четырем». четырем». пяти». пяти». Первое высказывание истинно Первое высказывание Второе высказывание ложно Второе высказывание истинно (А = 1). (А = 1). ложно (В = 0). (В = 0).

Логическое умножение Логическое умножение (конъюнкция)  (конъюнкция Объединение двух (или нескольких) Объединение двух (или нескольких) высказываний в одно с помощью союза «ии» » высказываний в одно с помощью союза « называется называется операцией логического умножения или или операцией логического умножения Составное высказывание, образованное Составное высказывание, образованное конъюнкцией..  конъюнкцией в результате операции логического в результате операции логического умножения (конъюнкции), истинно истинно умножения (конъюнкции), тогда и только тогда, когда истинны тогда и только тогда, когда истинны все входящие в него простые все входящие в него простые высказывания.. высказывания 1) «2  2 = 5 и 3 1) «2 2) «2  2 = 5 и 3 2) «2 3) «2  2 = 4 и 3 3) «2 4) «2  2 = 4 и 3 4) «2 3 = 10» (ложно) 2 = 5 и 3  3 = 10» (ложно) 2 = 5 и 3  3 = 9» 3 = 9» (ложно) (ложно) 2 = 4 и 3  3 = 10» 3 = 10» (ложно) (ложно) 2 = 4 и 3  3 = 9» (истинно) 3 = 9» (истинно)

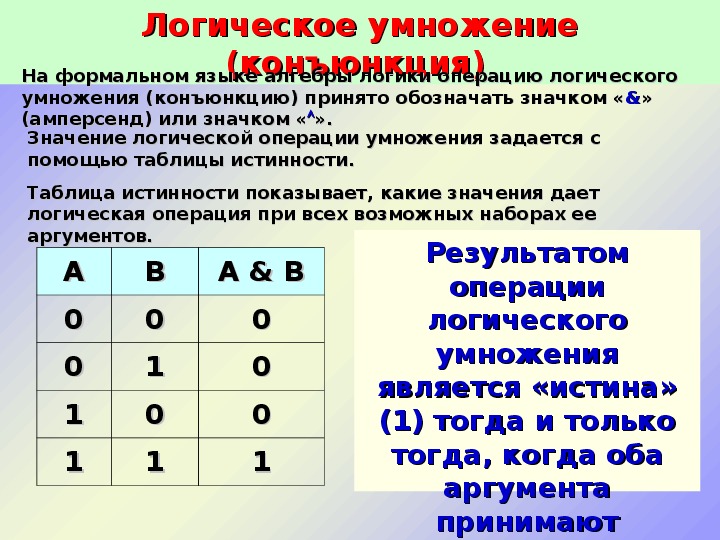
Логическое умножение Логическое умножение (конъюнкция) (конъюнкция) На формальном языке алгебры логики операцию логического На формальном языке алгебры логики операцию логического умножения (конъюнкцию) принято обозначать значком «&&» » умножения (конъюнкцию) принято обозначать значком « (амперсенд) или значком «».».  (амперсенд) или значком « Значение логической операции умножения задается с Значение логической операции умножения задается с помощью таблицы истинности. помощью таблицы истинности. Таблица истинности показывает, какие значения дает Таблица истинности показывает, какие значения дает логическая операция при всех возможных наборах ее логическая операция при всех возможных наборах ее аргументов. аргументов. ВВ 00 11 00 11 является «истина» является «истина» (1) тогда и только (1) тогда и только тогда, когда оба тогда, когда оба Результатом Результатом операции операции логического логического умножения умножения АА 00 00 11 11 А & В А & В 00 00 00 11 аргумента аргумента принимают принимают значения «истина» значения «истина»

Логическое сложение (дизъюнкция)  Логическое сложение (дизъюнкция) Объединение двух (или нескольких) Объединение двух (или нескольких) высказываний в одно с помощью союза «илиили» » высказываний в одно с помощью союза « называется называется операцией логического сложения или или операцией логического сложения Составное высказывание, образованное Составное высказывание, образованное дизъюнкцией. . дизъюнкцией в результате операции логического в результате операции логического сложения (дизъюнкции), истинно истинно сложения (дизъюнкции), тогда, когда истинно хотя бы одно из тогда, когда истинно хотя бы одно из входящих в него простых входящих в него простых высказываний.. высказываний 2 = 5 или 3  3 = 10» 1) «2  2 = 5 или 3 3 = 10» 1) «2 2) «2  2 = 5 или 3 2 = 5 или 3  3 = 9» 3 = 9» 2) «2 (истинно) (истинно) 2 = 4 или 3  3 = 10» 3 = 10» 3) «2  2 = 4 или 3 3) «2 2 = 4 или 3  3 = 9» 3 = 9» 4) «2  2 = 4 или 3 4) «2 (истинно) (истинно) (ложно) (ложно) (истинно) (истинно)

Логическое сложение (дизъюнкция)  Логическое сложение (дизъюнкция) На формальном языке алгебры логики операцию логического На формальном языке алгебры логики операцию логического операцию логического сложения (дизъюнкцию) принято операцию логического сложения (дизъюнкцию) принято обозначать значком «». ». обозначать значком « Значение логической операции сложения задается с Значение логической операции сложения задается с помощью таблицы истинности. помощью таблицы истинности. АА 00 00 11 11 ВВ 00 11 00 11 А А vv В В 00 11 11 11 Результатом Результатом операции операции логического логического сложения сложения является «ложь» является «ложь» (0) тогда и только (0) тогда и только тогда, когда оба тогда, когда оба аргумента аргумента принимают принимают значения «ложь» значения «ложь» (0). (0).

Логическое отрицание (инверсия)  Логическое отрицание (инверсия) Присоединение частицы «нене» к высказыванию » к высказыванию Присоединение частицы « называется операцией логического отрицания операцией логического отрицания называется или инверсией инверсией. . или Логическое отрицание (инверсия) Логическое отрицание (инверсия) получает из истинного высказывания получает из истинного высказывания ложное и, наоборот, из ложного — ложное и, наоборот, из ложного — истинное. истинное. Высказывание «Два умножить на два Высказывание «Два умножить на два равно четырем» истинно. равно четырем» истинно. Высказывание, образованное с Высказывание, образованное с помощью операции логического помощью операции логического отрицания, «Два умножить на два нене отрицания, «Два умножить на два равно четырем» ложно. равно четырем» ложно.

Логическое отрицание (инверсия) Логическое отрицание (инверсия) На формальном языке алгебры логики операцию На формальном языке алгебры логики операцию логического отрицания (инверсию) над логическим логического отрицания (инверсию) над логическим высказыванием А принято обозначать или А, или принято обозначать или А, или  А А..  высказыванием А Значение логической операции отрицания задается с Значение логической операции отрицания задается с помощью таблицы истинности. помощью таблицы истинности. АА 00 11 А А 11 00 Результатом Результатом операции операции логического логического отрицания является отрицания является «истина» (1), когда «истина» (1), когда аргумент принимает аргумент принимает значение «ложь» (0), значение «ложь» (0), и значение «ложь» и значение «ложь» (0), когда аргумент (0), когда аргумент принимает значение принимает значение «истина» (1). «истина» (1).

2) Когда результатом операции 2) Когда результатом операции логического сложения (дизъюнкции) логического сложения (дизъюнкции) является «истина»? является «истина»? 3) Когда результатом операции 3) Когда результатом операции логического отрицания (инверсии) логического отрицания (инверсии) является «истина»? является «истина»? 1) Когда результатом операции 1) Когда результатом операции логического умножения (конъюнкции) логического умножения (конъюнкции) является «истина»? является «истина»? 4) Как называется таблица, которая 4) Как называется таблица, которая показывает, какие значения даёт показывает, какие значения даёт логическая операция при всех логическая операция при всех возможных наборах ее аргументов. возможных наборах ее аргументов.