Методы и приемы обучения математике направленные на предупреждение ошибок и затруднений, их коррекцию

Для того чтобы систематизировать и квалифицировать ошибки, которые совершают обучающиеся в контрольных, самостоятельных и домашних работах, выделено 12 основных видов ошибок, благодаря которым можно понять основные причины появления затруднений.

Виды ошибок:

1. Решение даже не начато

2. Вычислительная ошибка в элементарном действии

3. Вычислительная ошибка в многошаговом действии

4. Установление неправильных связей между данными задачами

5. Неправильное понимание условий задачи

6. Ошибки при переписывании

7. Незнание алгоритмов математических действий

8. Неэквивалентные преобразования

9. Ошибки геометрических измерений

10. Незнание математических формул

11. Незнание законов арифметики

12. Логические ошибки

Все без исключения школьники совершают вычислительные ошибки. Для того чтобы снизить их количество в многошаговых арифметических действиях, необходимо обучать детей алгоритмам, которые позволяют разбивать сложные действия на более простые.

Однако для выделения элементарных действий предварительно следует установить уровень заданий, который будет доступен каждому обучающемуся. К такому уровню могут быть отнесены:

• вычитание/сложение однозначных или двузначных чисел без перехода единиц в старший разряд;

• вычитание однозначных или двузначных чисел при условии, что число единиц в соответствующем разряде уменьшаемого больше числа единиц в разряде вычитаемого;

• умножение однозначных чисел между собой и умножение на двузначные числа при условии, что последние остаются двузначными;

• деление однозначных чисел, а также деление двузначных чисел на однозначные, но при этом делитель является делителем числа единиц в каждом разряде.

Другие арифметические действия целесообразно разбивать на элементарные.

Достаточно сложными для детей являются текстовые задачи, так как они предполагают применение не только знаний, которые были получены на уроках, но и своего жизненного опыта. Наиболее распространенная ошибка – неиспользование части условия текстового задания. В целях исключения таких ошибок необходимо, чтобы дети обладали устойчивыми навыками по решению элементарных текстовых задач. При этом уровень сложности задачи не должен ставить обучающегося в безвыходное положение.

Что касается ошибок переписывания, то они в основном возникают в случаях, когда задания неинтересны обучающемуся. Как только они становятся значимыми для него, то количество ошибок при переписывании резко уменьшается.

Для того чтобы снизить количество ошибок, связанных со сложением и вычитанием обыкновенных дробей, необходимо более детальное изучение типовых примеров решения данного вида задач.

В ходе решений простейших уравнений обучающиеся часто сталкиваются с проблемой приведения эквивалентных преобразований. Самые распространенные ошибки – определение знака одночлена, когда он переносится в другую часть уравнения, а также непонимание сущности числового коэффициента переменной.

Ошибки, которые связаны с геометрическими измерениями, в большинстве случаев объясняются элементарным отсутствием навыков работы с линейкой и транспортиром. Проблема устраняется за счет постоянного применения на уроках этих инструментов. В целях профилактики необходимо, чтобы обучающиеся точно понимали, что такое точка отсчета и единица измерения. Кроме того, до начала практических измерений следует закрепить соотношения используемых единиц одной физической величины.

В 5 классе одним из самых трудных разделов является тема, посвященная прямоугольным параллелепипедам. И если обучающийся не знает формул объема, то он просто не сможет решить ни одной задачи. Однако и в самих заданиях этой темы можно выделить объективные трудности, ведь от обучающегося требуется, чтобы он усвоил единицы объема и взаимоотношения между ними. Очень часто более слабые обучающиеся просто не понимают, как между собой соотносятся кубические метры и сантиметры, а также кубические километры и кубические метры. Кроме того, для решения многих задач требуется наличие пространственного воображения, поэтому некоторые обучающиеся испытывают затруднения при решении задач, где требуется определить объем тел, изображенных на чертежах и рисунках. В целях профилактики таких ошибок рекомендуется больше уделять времени изучению моделей, которые должны быть доступны каждому обучающемуся. Особенно высоких результатов можно добиться, если применять разборные модели параллелепипедов.

В процессе изучения арифметики значительное количество ошибок связано с применением распределительного закона умножения. Обучающиеся, которые не усвоили этот закон, при умножении одночлена на многочлен делают только одно действие умножения, а остальную часть многочлена записывают без каких-либо необходимых изменений. Профилактика ошибки заключается в использовании схемы умножения, в которой стрелками соединяются все сомножители.

Реже всего встречаются логические ошибки, однако это, прежде всего, связано с тем, что обучающиеся пятых классов крайне мало решают таких задач. Поэтому профилактика таких задач предполагает, в первую очередь, увеличение количества таких задач в учебных пособиях для 5 класса.

Методы, направленные на предупреждение ошибок

Задачи-ловушки

Провоцирующие задачи, то есть задачи, которые подталкивают обучающегося к неправильному выбору, обладают крайне высоким развивающим потенциалом. При попадании в подготовленную «ловушку» обучающийся начинает испытывать досаду и смущение от того, что он не придал значения каким-либо нюансам и условиям задачи. В результате обучающийся испытывает сильное впечатление и надолго запоминает свои ошибочные действия, а в дальнейшем уже на подсознательном уровне старается не попадаться в аналогичные ситуации.

Кроме того, задачи-ловушки способствуют развитию критичности, учат детей внимательно анализировать информацию, проводить ее разностороннюю оценку. Одновременно и повышается и интерес к изучению математики.

Выделяют несколько основных видов провоцирующих задач:

• задачи, в которых условия навязывают получение неправильного ответа;

• задачи, где условия делают подсказку на неправильный алгоритм решения;

• задачи, в которых неоднозначность трактовки терминов, используемых оборотов, числовых и буквенных выражений выводят на неправильный путь решения;

• задачи, где обучающемуся необходимо что-то придумывать, строить, составлять и т.д. В итоге у обучающегося должны получиться такие математические объекты, которые не могут иметь места при заданных условиях;

• задачи, в которых условия допускают возможность «опровержения» семантически верного решения каким-либо нематематическим способом.

Задачи, условия которых навязывают неверный ответ

А. Задачи, навязывающие в явной форме один вполне определенный ответ.

Пример.

Сколько цифр потребуется, чтобы записать одинадцатизначное число?

На первый взгляд кажется, что ответ очевиден – «11 цифр». Однако по причине того, что десятичная система счисления использует только 10 цифр, то правильным ответом будет: «Одинадцатизначное число можно записать с помощью 0,1,2,3,4,5,6,7,8,9 или 10 цифр».

Б. Задачи, стимулирующие сделать выбор ответа из предложенной совокупности изначально неверных ответов.

Пример.

Какое из чисел 205, 206, 207, 208, 209, 210 является простым?

В большинстве случаев ученики называют 209 или 207, но это неверно, так как все числа являются составными. Правильный ответ: «Никакое».

В. Задачи, где предлагается сделать неправильный выбор из совокупности верных и неверных ответов.

В каком из вариантов пример решен неверно?

Г. Задачи, где условия не содержат неверных ответов в явном виде, но при этом каким-то образом указывают на него.

Пример.

Какое простое число следует за числом 200?

Напрашивается ответ: 201, ведь это число следующее – за числом 200. Однако ответ неправильный, ведь число 201 является составным. Правильный ответ – 211.

Задачи, побуждающие к выбору неверного способа решения

А. Задачи, в которых условия подталкивают обучающегося выполнить определенные действия с предложенными числами, однако на самом деле этого не требуется делать.

Пример.

Тройка лошадей проскакала 12 км. Сколько километров проскакала каждая лошадь?

Многие ученики делят 12 на 3 и получают ответ 4 км. Однако все лошади проскакали по 12 километров.

Б. Задачи, где условия подталкивают выполнить определенное действие, хотя на самом деле требуется выполнить обратное действие.

Пример.

У палки 2 конца. Если один из них отпилить, сколько концов получиться?

С ходу хочется ответить, что следует выполнить вычитание 2 – 1, что приводит к ответу «у палки один конец». На самом же деле количество концов останется неизменным – 2 или второй вариант правильного ответа – получится две палки, а значит, будет уже 4 конца.

В. Задачи, где условия подталкивают обучающегося выполнить действие определенным образом, хотя надо действовать по-другому и при этом выполнять более сложный расчет.

Пример.

На руках 10 пальцев. Сколько пальцев на 10 руках?

Большинство учеников сразу же перемножают 10 на 10. Однако у человека на руке 5 пальцев, поэтому надо 5 умножать на 10 и правильный ответ – число 50.

Г. Задачи, которые предлагают выполнить действия, которые в принципе невозможно выполнить.

Пример.

Двое пошли, 3 гриба нашли. Четверо пойдут, сколько грибов найдут?

Напрашивается последовательность действий:

1) 4:2 = 2,

2) 3х 2 = 6,

т.е. четверо вроде бы найдут 6 грибов. Однако же они могут вообще ничего не найти, поэтому правильный ответ: «Неизвестно».

Задачи, которые вынуждают придумывать, составлять, строить и др. несуществующие при заданных условиях математические объекты

Пример.

Придумайте простое трехзначное число, в записи которого употребляются лишь цифры 1 и 4.

Придумать такое число просто невозможно, так как любое число, удовлетворяющее условию задачи, будет кратно 3 и, соответственно, не является простым.

Задачи, которые вводят в заблуждение из-за неоднозначности трактовки терминов, буквенных и числовых выражений

Пример.

На листке бумаги написано число 606. Какое действие нужно совершить, чтобы увеличить его в полтора раза?

Здесь имеется в виду, что надо совершать не математическое действие, а провести действие с листом бумаги. И если перевернуть листок, то с обратной стороны мы увидим число 909, которое как раз в 1,5 раза больше 606.

Задачи, где допускается возможность «опровержения» семантически верного решения нематематическим решением

Пример.

(Старинная задача). Крестьянин продал на рынке трех коз за 3 рубля. Спрашивается: «По чему каждая коза пошла?»

Очевидный ответ: «По одному рублю», но опровергается, так как козы по деньгам не ходят, а ходят по земле.

Логические ошибки

Возникновение логических ошибок связано с нарушениями основных принципов математических рассуждений.

Наиболее часто встречаются ошибки в определении понятия, например:

• квадратное уравнение с одним неизвестным – уравнение, которое содержит неизвестное второй степени;

• равносильные уравнения – уравнения, где корни первого уравнения выступают в роли корней второго уравнения;

• отрезок, которые соединяет середины сторон треугольника и равный половине его третьей стороны, называется средней линией треугольника;

• прямая, которая разделяет сторону треугольника пополам, называется медианой.

В данных примерах нарушено ключевое требование к установлению определения понятия, то есть наличие достаточных признаков объекта. Для профилактики появления таких ошибок требуется тщательная отработка определения понятий, в том числе с использованием метода сравнения объектов и различных примеров с опровержениями.

Для закрепления понятий целесообразно предложить детям решение следующих примеров:

1. Являются ли равносильными уравнения:

1. х – 2 = 0 и (х – 2) (х – 3) = 0;

2. х – 2 = 0 и х + 3 = 5;

2. Какие из нижеприведенных уравнений являются квадратными:

1. х2 – 3х + 2 = 0;

2. х3 – х2 + 3х = х3 – 2;

3. х3 + х2 – 3х = х3 – 2;

4. х2 – 4.

Ошибки при доказательстве теорем

При доказательстве теорем довольно часто обучающиеся используют искомое в качестве данного. Для предупреждения такой ошибки необходимо четко объяснять обучающимся, что дано и что требуется доказать.

Часто встречаются и логические ошибки в доказательстве утверждений, которые заключаются в неполной аргументации или пропуске аргументации.

Неполная дизъюнкция также является логической ошибкой и преимущественно допускается в вопросах и задач, которые связаны с исследованием.

Пример:

Необходимо установить сравнительную величину а3 и а2. Вместо того чтобы проверить все возможные значения буквы а, обучающийся начинает рассматривать значения выражений только при а > 1, в результате чего получает неполный ответ.

Много ошибок дети допускают в преобразованиях алгебраических выражений, что связано с применением необоснованной аналогии. Примером такой ошибки может служить следующее выражение: так как (a + b)c = ac + bc, то по аналогии (ab)c = ac(bc. Известно, что, если а = b, то ak = bk, отсюда по аналогии считают, что, если a > b, то ak > bk в любом случае; по аналогии с численными дробями обучающиеся иногда считают, что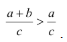

Для профилактики ошибок необходимо обучающимся постоянно устно напоминать и демонстрировать примеры того, что аналогия выступает только как вспомогательное средство для установления истины и в каждом случае требует выполнения проверки и подтверждения логическим доказательством.

Наиболее распространенные ошибки, совершаемые обучающимися выпускных классов

Задание.

Очень часто обучающиеся применяют неверную формулу, даже не задумываясь над ней. Так, при определении того является ли число

использовании определения степени в похожих случаях обучающиеся могут вывести любую формулу действий со степенями. Аналогичным образом учитель может продемонстрировать ошибки в действиях со степенями.

Обучающимся также можно показать три варианта решения данного неравенства:

При выполнении тригонометрических заданий школьники часто сами придумывают формулы, к примеру: «sin 2 х = 2 sin x».

В таких случаях можно действовать двумя способами:

При этом учителю не требуется целенаправленно проводить исправление всех ошибочных утверждений обучающегося и рассказывать ему обо всех ошибках. Оптимальный вариант – обсудить ошибку всем классом и добиться того, чтобы все обучающиеся поняли причину ее появления и в дальнейшем не допускали ее. Как свидетельствует практический опыт, организация систематических проверок чужих записей позволяет сформировать у школьников привычку критически относиться и к своим записям.

Для этого отлично подходят задания, где надо найти ошибку в решении, например:

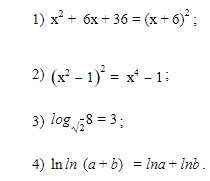
Процесс поиска и исправления ошибок самим обучающимся под руководством педагога является весьма поучительным для всех обучающимися, так как в ходе данного процесса изучение и анализ ошибок способствует развитию познавательного интереса к изучению математики.

Основные ошибки, обучающиеся допускают в следующих ситуациях:

• выполнение исследования функции на наименьшие и наибольшие значения;

• преобразование дробно-рациональных выражений, где содержится корень n-ой степени;

• вычисление площади криволинейной трапеции;

• решение показательных и логарифмических неравенств;

• изображение тел вращения при решении геометрических задач;

• построение графика функции, содержащей модуль;

• построение множества точек плоскости, которое должно удовлетворять заданному условию;

• теоретическое обоснование применяемых формул и фактов при выполнении задач по стереометрии;

• решение задач с параметром.

В целях повышения уровня учебных успехов обучающихся, а также в ходе подготовки к итоговой аттестации за курс старшей школы целесообразно повышенное внимание уделять следующим темам:

• углы в пространстве;

• комбинация тел;

• построение геометрических мест точек, удовлетворяющего установленным условиям;

• производная и ее применение при исследовании функции на отрезке;

• тригонометрические функции и их свойства;

• логарифмические и показательные неравенства;

• тождественные преобразования дробно-рациональных выражений, где содержится корень n-ой степени.

Целесообразно спланировать учебный процесс таким образом, чтобы учебный год в выпускных классах заканчивался повторением всего пройденного материала. При этом повторение должно быть нацелено на закрепление опорных знаний, подготовку к итоговому оцениванию знаний, а также формирование и развитие межпредметных связей с одновременным осознанием взаимосвязи с ранее пройденными темами.

При высоком уровне организации учителем работы учеников над типичными ошибками позволяет существенно повысить уровень обучения математике и способствует развитию логического мышления.

Особенность школьной программы состоит в том, что при оформлении упражнений используется не математический характер и существующие правила абсолютно не связаны с проверкой знаний. Особенно это остро ощущают сильные обучающиеся, которые справедливо раздражаются из-за того, что два незначительных недочета являются ошибкой.

Намного правильнее было бы, если к математическому тексту предъявлялось одно требование – ясное отражение логики решения. При этом должно быть абсолютно неважно, какие слова и выражения использовал обучающийся для объяснения своих действий. Кстати, именно такие правила используются в высших учебных заведениях, где преподаватель смотрит исключительно на логику решения задачи.

Например, по вузовским стандартам следующая записи

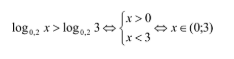
является полностью исчерпывающей и не предполагает какого-либо дополнительного словесного комментария. Ведь важно, чтобы обучающийся правильно преобразовал неравенство, а не использовал при объяснении фразу: «Так как основание логарифма меньше единицы, то функция убывает и знак неравенства меняется».

Современные экзамены по своему характеру максимально приближены к тестированию, поэтому к оформлению предъявляется всего одно требование – разборчивая запись ответа.

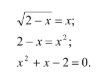
По теореме Виета х1 = 1, х2 = -2.

Проверка показывает, что х2 не удовлетворяет условию. Ответ: 1.

Данное решение в большинстве случаев оценивается положительно. В тоже время такая последовательность действий оставляет несколько неясностей:

1. Зачем нужно было искать ОДЗ, если он в решении не использовался.

2. Один из предложенных корней не удовлетворяет условию, поэтому надо выяснить, откуда он здесь появился.

3. Какие логические знаки необходимо применять для связывания сделанных записей.

4. В соответствии с каким математическим законом х1 и х2 являются значениями переменной х.

И если пункты 1, 2, 4 можно считать еще придирками, то отсутствие логических знаков (пункт 3) является уже серьезной ошибкой. Для справедливости стоит отметить, что такая ошибка присутствует во многих работах обучающихся.

Для сравнения можно привести другой вариант решения: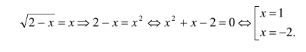

В связи с тем, что возведение в квадрат могло стать причиной появления посторонних корней, то требуется проверка.

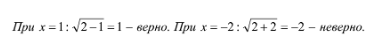Ответ: 1.

Если вместо первой импликации «(» ученик напишет «(», то это будет ошибкой. Если же любую из оставшихся эквиваленций «(» заменить на «(», то все останется верным.

В первом варианте решения обучающийся, скорее всего, просто не задумывался о логических связях записей и просто механически разделял записи с помощью «точки с запятой». И если бы «точка с запятой» использовалась только в одном определенном смысле, то было все нормально. Однако данный символ в работах школьников может быть заменой различных символов, в том числе:

• «равносильно»;

• «следовательно»;

• «и»/«или»;

• объединение и пересечение множеств.

Организация контроля и самоконтроля учебной деятельности обучающихся

При проверке работ педагог отмечает не только математические, но и грамматические, и стилистические ошибки. При этом учитель лично исправляет все ошибки, что является крайне неверным решением. Ведь если учитель исправил ошибку, то обучающийся просто соглашается с ней и успокаивается.

Для повышения уровня самостоятельной работы обучающегося необходимо, чтобы он сам выявил свою ошибку и разобрался, почему он ее совершил. Поэтому учителю достаточно просто указать место ошибки, для чего может использоваться определенная символьная система. Так, две черты обычно указывают на грубую ошибку, одна черта – случайная или негрубая ошибка, а волнистая линия – наличие какого-либо недочета.

При проверке домашних заданий учителю необходимо тщательно просматривать все проведенные обучающимся преобразования, вычисления и рассуждения. При этом все ошибки требуется систематизировать и выделить наиболее типичные и массовые. В первую очередь, выделяются наиболее грубые и принципиальные ошибки, которые связаны с нарушением основных математических законов.

Именно таким ошибкам и необходимо уделять повышенное внимание при проведении разбора в классе. Такой обзор нельзя ограничивать только сообщением ошибок каждого обучающегося, так как требуется произвести разбор ошибок и выявить причины, которые к ним привели. Для этих целей целесообразно привлекать и других обучающихся, которые допустили аналогичные ошибки.

Если какое-то задание вызвало затруднения у большинства обучающихся класса, то его надо разбирать максимально детально и при необходимости провести дополнительные упражнения.

Если ошибка не была массовой, то обучающемуся можно предложить произвести детальный ее разбор дома, внести все необходимые исправления и сделать отсылки на соответствующие правила.

Для повышения эффективности работы над ошибками нельзя откладывать проведение этого мероприятия, так как отсрочка неизбежно ведет к потере интереса учеников к разбору.

Для того чтобы исправить множество ошибок и предупредить их появление, крайне важно сформировать у обучающихся навыков самоконтроля, которые включают в себя две части:

• способность самостоятельно обнаруживать ошибки;

• умение самостоятельно объяснить ошибку и исправить ее.

Для поиска ошибок используются следующие приемы:

• проверка правильности проведенных вычислений и преобразований за счет выполнения обратного действия либо преобразования;

• проведение оценки полученного результата с точки зрения здравого смысла;

• осуществление проверки правильности решения за счет составления и решения задач, обратных решаемой задаче;

• проверка правильности решения с помощью графического способа.

Формированию навыков самоконтроля способствует и прием приближенной оценки ожидаемого результата, ведь установление возможных пределов планируемого результата позволяет не допустить недочеты в виде описок и пропуска цифр.

К примеру, обучающемуся надо решить следующую задачу: «За неделю завод выпустил 130 телевизоров, выполнив месячный план на 25%. Сколько телевизоров должен выпустить завод за месяц по плану».

Ученик написал 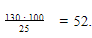Ошибку можно сразу вычислить, если перед решением школьник «включит» логику и прикинет «В течение недели было выпущено 130 телевизоров. Соответственно, за месяц будет выпущено больше 130 телевизоров, поэтому и ответ должен быть больше 130».

Система работы учителя математики по коррекции ошибок Достижение положительного эффекта от индивидуальных заданий объясняется тем, что обучающиеся их выполняют самостоятельно, в том числе и дома. В то же время индивидуальные задания должны составлять методически правильно и быть направлены на преодоление конкретных ошибок. Для этого от учителя требуется постоянное ведение учета основных затруднений обучающихся, для чего, например, может использоваться следующий вариант таблицы:

Список учащихся класса	Тема…			Примечание «+» - ошибка устранена; «-» - ошибка не устранена
	Пробелы в знаниях	Классные индивидуальные задания	Домашние индивидуальные задания

Заполнение всех граф таблицы, за исключением первой, рекомендуется осуществлять карандашом. Пополнение списка ошибок ведется при проверке домашних заданий, самостоятельных и контрольных работ. Большинство ошибок повторяются из года в год, поэтому молодому педагогу рекомендуется ознакомиться с ними.

Ниже представлены наиболее распространенные ошибки.

При работе с десятичными дробями обучающиеся совершают ошибки в выделении целой части результата, к примеру:

а) 3,6 – 1,8 = 18;

б) 2 + 5,3 = 55;

в) 6,4 : 2 = 32.

Во время беседы с обучающимися, которые допускают такие ошибки, обычно выясняется, что они просто забыли поставить запятую. Устранение ошибки осуществляется в результате длительных тренировок.

Одна из самых типичных ошибок – деление десятичной дроби на десятичную. Деление обычно совершается без обращения внимания на запятые: 2,576: 11,2 = 23.

Для профилактики ошибок обучающимся предлагаются задания на карточках, где для каждого примера приведено соответствующее правило, но оно сформулировано с пропусками или полностью.

Примеры карточек.

Карточка №1. Чтобы сложить две десятичные дроби, надо:

1. сложить получившиеся числа, как складывают ...;

2. записать слагаемые друг под другом так, чтобы запятая ...;

3. уравнять число знаков ... в слагаемых;

4. в полученной сумме поставить запятую под....

Задания.

1. В представленных числах уравняйте число знаков после запятой: 2,5; 0,25; 43, 1256; 325,1.

2. Выполните сложение дробей: 12,7 и 3,442; 0,237 и 10,44.

Карточка № 2.

Для того чтобы умножить одну десятичную дробь на другую, надо выполнить умножение, не обращая внимание на ..., а затем в результате отделить запятой... столько цифр, сколько их стоит после запятой... .

Задания.

1. В записи числа 1234567 отделите запятой справа:

   1. одну цифру;
   2. две цифры;
   3. шесть цифр;
   4. семь цифр.

В каком случае в результате получается число, которое больше 1, но меньше 2? больше 0, но меньше 1?

2. Найдите произведение чисел: 2,7 и 1,32.

Карточка № 3.

Чтобы разделить число на десятичную дробь, надо в делимом и в делителе перенести ... вправо на столько цифр, сколько их после... в ..., а потом выполнить деление на натуральное число.

Задания.

1. В записи 4,78: 0,8 подчеркните одной чертой делимое, а двумя – делитель.

2. В числах 1; 0,345; 30,25 перенесите запятую вправо на столько цифр, сколько их после запятой в числе 0,5.

3. Найдите частное чисел: 8,96 на 1,12.

Часто встречаются ошибки при совершении действий с обыкновенными дробями. В частности, при выполнении сложения (вычитания) дробей обучающиеся производят складывание (вычитание) числителей и знаменателей: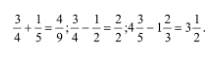

Складывая (вычитая) дроби, обучающиеся забывают умножить их числители на дополнительные множители:

Карточка № 5.

Известно, что вычитание проверяется и тем, что разность двух положительных чисел не может быть больше уменьшаемого.

1. Учитывая сказанное выше, установите, верен ли результат вычитания:

При умножении (делении) смешанного числа на десятичную дробь умножают (делят) отдельно целые части и отдельно дробные, а результаты записывают рядом, например:

Приемы работы по повышению качества работы по профилактике ошибок

Существует несколько основных правил, при руководстве которыми можно значительно снизить количество ошибок. При этом многие формулировки относятся к фольклорному жанру, но, тем не менее, дают объективное понимание какого-либо правила:

1. Правило ГАИ. Оно гласит, что большинство аварий случается при небольших скоростях. При переносе данного тезиса на математику получаем, что большинство ошибок возникают в самых простых ситуациях.

Для непопадания в такие ситуации обучающимся надо привить навык постоянной проверки правильности списывания условий задач, решения квадратных уравнений. А для выявления ошибки рекомендуется начинать ее искать с конца, что предполагает подстановку полученного результата в последнее действие и последовательное следование выше.

Правило закройщика: шов иголкой делается следующим образом: стежок вперед и назад, а потом еще вперед и опять назад.

В математике преобразования осуществляются аналогичным образом, то есть после совершения каждого перехода необходимо «оглянуться назад» и проверить полученный результат проведением обратного преобразования.

2. Правило программиста: работай блоками.

В программировании произвести отладку программы целиком невозможно, поэтому всю работу разбивают на небольшие автономные блоки, и затем по отдельности проверяется работоспособность каждого блока.

В математике этим правилом необходимо руководствоваться, прежде всего, при работе с громоздкими выражениями, то есть они разбиваются на несколько простых. При решении с каждым уравнением «разбираются» по отдельности.

Большинство приемов работы над ошибками не содержит методик диагностики выявления причин ошибок, а также не уделяется достаточного внимания работе по организации рефлексивной деятельности учеников и ее применения для предупреждения и исправления математических ошибок.

Еще один недостаток состоит в том, что работа над ошибками практически никак не контролируется, поэтому причины появления ошибок так и остаются не выясненными и повторяются снова и снова. Для повышения качества работы над ошибками необходимо обеспечивать большую самостоятельность учеников, так как это позволяет осуществлять более осознанный анализ ошибок и собственных действий при решении конкретной задачи.

В результате у обучающихся развивается логическое мышление, а также создаются благоприятные условия для лучшего усвоения новых знаний. Постепенно у детей развиваются и стремление самостоятельно разобраться в задаче, умение по планированию ее решения и навыки продумывания различных вариантов действий. Например, обучающийся отлично усвоил правило преобразования алгебраических выражений формулы квадрата суммы и разности двух чисел, однако, когда получает задание, где необходимо представить в виде многочлена (–х–5)2, он теряется.

В таких случаях обучающемуся надо предложить ответить на вопрос, что конкретно у него вызывает затруднение? Далее надо помочь ему преобразовать выражение таким образом, чтобы можно было использоваться одну из известных ему формул в том виде, в каком они представлены в учебнике.

Еще один пример неосознанного применения алгоритма:

Обучающемуся предлагается решить уравнение sin x = 1,2, он сразу же начинает искать его корни по уже отлично известной ему формуле и при этом совершенно не обращает внимания на недопустимые значения sin x. Для того чтобы помочь учащемуся разобраться в данной ситуации, рекомендуется продемонстрировать наглядное решение задачи на тригонометрическом круге.

Список литературы:

1. Азиев И.К. Индивидуальные задания для устранения ошибок. // Журнал «Математика в школе» – 1993 г. – №5, с. 9.
2. Волович И.Б. Наука обучать: Технология преподавания математики. – М.: LINKA-PRESS. 1995. – 280 с.
3. Гальперин П.Я. Методы обучения и умственное развитие ребенка. – М.: Изд-во Моск. Ун-та, 1985. – 45 с.
4. Гласс ДЖ., Стенли Дж. Сатистические методы в педагогике и психологии. Пер. С англ. – М.: Прогресс. – 1976. – 495 с.
5. Грабарь, И. И. Применение математической статистики в педагогических исследованиях. Непараметрические методы / И. И. Грабарь, К. А. Краснянская. – М.: Педагогика, 1977. – 136 с.
6. Груденов Я.И. Совершенствование методики работы учителя математики: Кн. для учителя. – М.: Просвещение, 1990. – 224 с.
7. Груденов, Я. И. Изучения определений, аксиом, теорем / Я. И. Груденов. – М. Просвещение, 1984. – 95 с.
8. Груденов Я.И. Психологический анализ причин некоторых массовых ошибок учащихся// Журнал «Математика в школе» – 1981 г. – №3, с. 46-48.
9. Груденов Я.И. Психолого-дидактические основы методике обучения математики. – газета «Математика», 1987 г. с. 91-96.
10. Гуцанович С.А. Дидактические основы математического развития учащихся: Монография. – Минск: БГПУ им. М. Танка, 1999. – 301 с.
11. Гуцанович С.А., Радьков А.М. Тестирование в обучении математике диагностико-дидактические основы. – Могилев, МГПИ им. А.А. Кулешова, 1995. – 203 с.
12. Давыдов В. В. Проблемы развивающего обучения. Опыт теоретического и экспериментального исследования / В. В. Давыдов. – М.: Педагогика, 1986. – 239 с.
13. Далингер В.А. Методика реализации внутрипредметных связей при обучении математике: Кн. для учителя. – М.: Просвещение, 1991. – 80 с.
14. Далингер В.А. Обучение учащихся доказательству теорем: Учебное пособие. – Омск: Омский пед. ин-т, 1990. – 127 с.
15. Действующие учебники и учебные пособия по математике для средней школы.
16. Журналы «Математика в школе» за 1970-1990 гг.
17. Зайкин М.И., Колосова В.А. Провоцирующие задачи // Журнал «Математика в школе» – 1997 г. – №6, с. 32.
18. Запрудский Н. И. Современные школьные технологии: пособие для учителей. – 3-е изд. / Н. И. Запрудский. – Минск, 2006. – 288 с.
19. Колягин Ю.М. Задачи в обучении математике: Математические задачи как средство обучения и развития учащихся: в 2ч. – М.: Просвещение, 1977. – ч.2. – 144 с.
20. Колягин Ю.М. Задачи в обучении математике: Обучение математике через задачи и обучение решению задач: в 2ч. – М.: Просвещение, 1977. – ч.2. – 144 с.
21. Метельский Н.В. Дидактика математики. – Минск: Изд-во БГУ, 1982–254с.
22. Метельский Н.В. Пути совершенствования обучения математике: Проблемы современной, методики математики. – Минск: Университетское, 1989. – 160 с.
23. Методика преподавания математики в средней школе: Общая методика: учеб. пособие; сост. Р. С. Черкасов, А. А. Столяр. – М.: Просвещение, 1985. – 336 с.
24. Новик И.А. Формирование методической культуры учителя математики в педвузе. – Мн.: БГПУ им. М. Танка, 2002. – 193 с.
25. Новик, И. А. Практикум по методике преподавания математики / И. А. Новик. – Минск: Выш. шк., 1984. – 175 с.
26. Оганесян В.А. Принципы отбора основного содержания обучения математике в средней школе. – Ереван: Луис, 1984. – 215 с.
27. Рогановский Н. М. Методика преподавания математики в средней школе: учеб. пособие / Н. М. Рогановский. – Минск: Выш. шк., 1990. – 267 с.
28. Селевко Г. К. Современные образовательные технологии: учеб. пособие / Г. К. Селевко. – М.: Народное образование, 1998. – 256 с.
29. Скобелев Г.Н. Контроль на уроках математики: Пособие для учителя. – Минск: Народная асвета, 1986. – 103 с.
30. Столяр А.А. Роль математики в гуманизации образования // Математика в школе. 1990. – № 6. – с. 5–7.
31. Столяр А. А. Педагогика математики: учеб. пособие / А. А. Столяр. – Минск: Выш. шк., 1986. – 414 с.
32. Темербекова А. А. Методика преподавания математики: учеб. пособие / А. А. Темербекова. – М.: ВЛАДОС, 2003. – 176 с.
33. Фарков А. В. Внеклассная работа по математике.
34. Фридман, Л. М. Как научиться решать задачи: пособие для учащихся / Л. М. Фридман, Е. Н. Турецкий – 2- изд. – М.: Просвещение, 1984. – 175 с.
35. Фридман, Л. М. Психолого-педагогические основы обучения математике в школе / Л. М. Фридман. – М.: Просвещение, 1983. – 160 с.
36. Чаплыгин В.Ф. Некоторые методические соображения по решению текстовых задач // Журнал «Математика в школе» – 2000 г. – №4, с. 28.
37. Шнейдерман М.В. Анализ ошибок и затруднений учащихся V классов // Журнал «Математика в школе» – 1999 г. – №6, с. 21.
38. Эрдниев, П. М. Обучение математике в школе. Укрупнение дидактических единиц / П. М. Эрдниев, Б. Л. Эрдниев. – М.: Столетие, 1996. – 320 с.
39. Якиманская И.С. Личностно-ориентированное обучение в современной школе – М., 1996. – 347 с.
40. Якиманская И.С. Психологические основы математического образования. – М.: Acadiia, 2004.
41. Ярский А.С. Что делать с ошибками // Журнал «Математика в школе» – 1998 г. – №2, с. 8-14.