Функции математических задач и их реализация в процессе обучения математике

Наиболее распространенной в методической литературе классификацией задач является классификация, основанием для которой служит выполняемая задачей функция. С точки зрения выполняемых функций задачи подразделяют на:

• задачи с дидактическими функциями;
• задачи с познавательными функциями;
• задачи с развивающими функциями.

В процессе обучения математике выделяют следующие функции:

Задачи как средство:

• обучения математической деятельности;
• формирования знаний, умений и навыков;
• обучения моделированию явлений действительности;
• организации исследовательской деятельности;
• достижения метапредметных результатов;
• развития обучающихся (в частности – мышления, стилевой гибкости);
• воспитания (посредством организации общения и содержания самих задач) и в частности – ценностного отношения к математическим знаниям.

2. Задачи как метод обучения.

Задачи как метод обучения предполагают соответствующую структуру учебного процесса, в ходе которого учащиеся приобретают теоретические знания посредством решения задач. Построенный курс был предложен А.М. Астрябом в начале XX в. [1], а среди современных пособий, опирающихся на такой подход, можно выделить пособие В.В. Орлова «Геометрия в задачах: 7 – 9 класс» [5].

3. Задачи как цель обучения:

Если задача рассматривается как цель обучения, то обучающийся в результате ее решения усваивает понятие задачи, ее структуру, компоненты; процесс решения, приемы работы с текстом задачи, способы решения отдельных видов, общие методы поиска решения.

Очевидно, что одна и та же задача в зависимости от текущих целей обучения и своего места в системе задач может выполнять различные функции.

Рассмотрим более подробно, как реализуют свои функции те или иные задачи в процессе обучения математике.

Математические задачи как средство обучения, воспитания и развития

По своему функциональному назначению задачи как средство обучения могут быть направлены или на формирование знаний, умений и навыков учащихся (обучающие задачи), или на осуществление контроля со стороны учителя или учащихся уровня сформированности знаний, умений и навыков (контролирующие задачи).

Обучающие функции задачи, прежде всего, связаны с формированием элементов теоретических знаний и связанных с ними умений.

В системе задач, направленных на усвоение нового понятия и его определения, выделяют задачи:

• на раскрытие практической значимости понятия или его значимости для дальнейшего продвижения в изучении математики;

• на актуализацию знаний и умений, необходимых при формировании понятия;

• на выделение существенных признаков понятия;

• на распознавание понятия;

• на усвоение текста определения понятия;

• на использование математической символики;

• на установление свойств понятия;

• на применение понятия;

• на усвоение математических понятий;

• на овладение математической символикой.

К числу общих обучающих функций задач относятся:

1. Формирование у учащихся некоторого понятия (на уровне представлений о нем, на уровне его усвоения и на уровне закрепления).

2. Установление различных связей между понятиями (от рода к виду, внутри предметные и межпредметные связи и т. д.).

3. Формирование описания, определения понятия; подведение объекта под понятие.

4. Формирование ведущих идей, законов, суждений.

5. Установление различных связей между ведущими идеями, законами, суждениями; структурных соотношений между ними, иерархии.

6. Формирование основных видов умозаключений, способов и приемов их проведения.

7. Формирование ведущих умений и навыков, характерных для данного учебного предмета.

8. Формирование умений и навыков выражения мысли в речи и записи.

9. Формирование умений и навыков моделирования учебного материала (чертежи, графики и т. п.).

10. Формирование умений и навыков в обращении с приборами, инструментами, таблицами, с учебной и справочной литературой. [2]

Задачи могут брать на себя воспитательную функцию, близкую к мировоззренческой: демонстрировать ценность математики как науки, определять место математического знания в мире. В школе обучение не мыслится в отрыве от воспитания. Обучая решению математических задач, учитель математики в то же время воспитывает учащихся, формирует у них качества, необходимые для жизни в современном обществе.

К числу общих воспитывающих функций задач относятся:

1. Формирование у обучающихся высокой степени сознательности, чувства ответственности перед обществом, социальной активности, оптимизма и гуманистической направленности.

2. Воспитание чувства товарищества, взаимопомощи, творческой инициативы, дисциплинированности и организованности.

3. Эстетическое воспитание учащихся (формирование чувства прекрасного, вкуса к прекрасному, потребности, желания и способности преобразовать окружающий мир и строить человеческие отношения по законам красоты, стремление пополнить свой запас художественных и эстетических знаний и т. д.).

4. Воспитание положительного отношения к учебной деятельности, развитие интереса к учебе, любознательности.

5. Формирование умений рационализировать свою учебную работу и приемы ее оформления; воспитание способности доводить любое учебное задание до конца; формирование критичности в оценке результатов своей работы, наряду с чувством уверенности в правильности ее выполнения.

Эффективность математических задач и упражнений в значительной мере зависит от степени творческой активности учеников при их решении.

Одно из основных назначений задач - активизация мыслительной деятельности обучающихся в ходе учебного занятия. Учитель должен понимать, что математические задачи должны активизировать мышление школьников, будить мысль детей, заставлять ее работать, развиваться, совершенствоваться. Также следует помнить о том, что при решении математических задач обучающиеся не только выполняют построения, преобразования и запоминают формулировки, но и обучаются логическому мышлению, умению рассуждать, сопоставлять и противопоставлять факты, находить в них общее и различное, делать правильные умозаключения.

Под развивающими функциями задач можно понимать такие их функции, которые направлены на развитие мышления обучающихся, на формирование качеств, присущих научному мышлению, на овладение приемами эффективной умственной деятельности. Такие функции делятся на общие и конкретные. Специальные развивающие функции математических задач:

• Умение математизировать простейшие ситуации жизненного характера, усматривать математические закономерности в окружающем мире.

• Умение предсказать (предположить существование того или иного факта или свойства, относящегося к математическим объектам с достаточной степенью правдоподобия).

• Умение доказать или опровергнуть то или иное математическое положение дедуктивным путем.

• Умение планировать поиск решения задачи, исключить из условия ненужные данные, дополнять недостающие, отбирать методы, средства и операции, необходимые для ее решения, умение осуществить проверку правильности решения.

• Иметь четкое представление о логической структуре курса математики, о том, что абстрактный характер математики является основной причиной ее многочисленных приложений в других науках, в технике, в народном хозяйстве.

• Умение формулировать определения математических понятий и умение соотнести то или иное понятие с данным определением.

• Умение быстро и правильно проводить вычисления с привлечением простейших вычислительных средств для облегчения исчисления на соответствующем его этапе; умение создать на основе теоретических знаний удобную вычислительную ситуацию, осуществлять проверку и прикидку правильности вычислений.

• Умение распознавать то или иное математическое понятие в различных ситуациях.

• Умение проводить исследование в простейших учебных ситуациях.

Приведем пример задачи, в которой математика способствует решению экологической проблемы:

Задача 1.

Экологи протестуют против большого объёма лесозаготовки. Председатель леспромхоза объясняет, что в лесу 99% сосен, и вырубке подлежат только сосны. После осуществления лесозаготовки останется 98% сосен. Экологи настаивают на своём. Кто прав, если объём лесозаготовки считается большим при вырубке более 30% всех деревьев леса?

Решение задачи демонстрирует правоту экологов:

Пусть х – остальные деревья, за исключением сосен.

До вырубки: х = 100% – 99% = 1% (деревьев)

Тогда всего деревьев: 100х.

После вырубки: х = 100% – 98% = 2%

Тогда всего деревьев: 50х.

Ответ: после вырубки деревьев станет вдвое меньше.

Существуют различные способы представления информации. Каждый человек имеет свой предпочитаемый стиль кодирования информации. С точки зрения психологии, существует четыре стиля:

• словесно-речевой;

• визуальный;

• предметно-практический;

• сенсорно-эмоциональный.

Эффективное владение информацией возможно лишь при условии владения всеми перечисленными стилями. В рамках курса математики можно формировать стилевую гибкость учащихся, предлагая задачи, закодированные разными способами и/или предполагающие перекодировку.

Приведём примеры.

Задача 2.

Девочки провели соцопрос в своём классе, чтобы выяснить, чем предпочитают заниматься их одноклассники (мальчики) во время поездки в метро. Данные они занесли в таблицу:

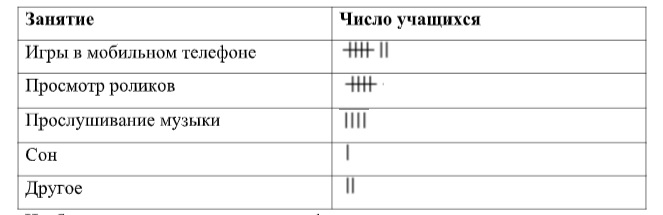
При составлении данной задачи (задача 2) использованы словесный и образно-иконический способы кодировки. Решение нужно закодировать образно-графическим способом. Задача, таким образом, предполагает внутриобразную перекодировку.Изобразите полученные данные графически.

Задача 3.

Футбольный мяч в результате удара по нему нападающим движется прямолинейно по закону

Установите:

1. ускорение движения мяча;

2. скорость полузащитника 15 км/ч, сможет ли он перехватить мяч на пятой секунде после удара?

Постройте график движения мяча.

Изобразите движение мяча у доски (роль мяча отводится отвечающему).

В данной задаче последнее задание (изобразить движение мяча у доски) демонстрирует один из способов включения в образовательный процесс сенсорно-эмоционального способа кодирования информации.

В современном мире одними из ключевых качеств мышления считаются гибкость и вариативность. Эти качества можно развивать на уроках математики, используя задачи с неоднозначными ответами и способами решения, задачи на несуществование, а также задачи, предполагающие несколько трактовок условия и требования.

Приведём примеры.

Задачи, которые предполагают несколько ответов:

Задача 4.

Определите объём ромбоэдра, если все его грани – ромбы с диагоналями 12 см и 16 см.

В данном примере мы имеем неоднозначность в условии: возможны четыре ситуации (диагонали выходят из одной вершины, но принадлежат разным граням): 12, 12, 12; 16, 16, 16; 12, 16, 12; 16, 12, 16. Значит, можно получить два разных ромбоэдра. Практика показывает, что решающие замечают только один ответ.

Задачи, которые развивают гибкость и вариативность мышления:

Задача 5.

Определите высоту трапеции ABCD, если боковые стороны АВ= 1 см и СD= 5 см. Основание ВС и диагональ ВD равны 5 см и 8 см соответственно.

Путем вычислений школьники отвечают на задание (определите высоту трапеции) – получают значение высоты. Так как учащиеся считают, что они ответили на вопрос задачи, то ее дальнейший анализ отсутствует. Ведь если сравнить полученную высоту с условием, то получится, что такой трапеции не существует: заданные стороны треугольника BCD, позволяющие получить высоту, ограничивают значение стороны АВ как наклонной, которая должна быть больше высоты.

Задача учит быть внимательным к условию и соизмерять полученные результаты с начальными данными и тем самым развивает гибкость мышления.

Задача с вариативностью ответов:

Задача 6.

Дан треугольник ABC. Сторона AB = 4 см, сторона BC = 6 см. Определите медиану, проведённую к стороне AC.

Ответ предполагает бесконечное множество чисел, но его область определения ограничена. Следовательно, ответ можно представить в непривычном для обучающихся виде – в виде интервала.

Задачи с неоднозначными ответами:

Задача 7.

Гипотенуза треугольника равна 10 см, высота - 6 см. Найдите площадь треугольника.

Задача на первый взгляд кажется неоднозначной: можно опустить высоту из вершины прямого угла, или же высота будет одним из катетов. Если в обоих случаях полученные, в конечном счете, площади совпадут, значит, мы имеем дело с неоднозначностью в условии. В случае несовпадения ответов имеет смысл проверить возможность существования обоих треугольников. И в таком случае окажется, что высота не может быть проведена из вершины прямого угла, т.к. она не должна превышать 5 см (медиана, проведённая из вершины прямого угла, равняется радиусу окружности с диаметром 10 см, а медиана является наклонной). Задача, вопреки первому предположению, оказывается однозначной. Так как данная задача предполагает рассмотрение нескольких ситуаций и пересмотра выдвинутого предположения о неоднозначности, его проверки и опровержение, значит, она способствует развитию гибкости и вариантности мышления и носит исследовательский характер.

Ещё одним важным свойством современного человека является наличие у него исследовательских и поисковых умений. Развитие соответствующих компетенций предопределено современными образовательными стандартами и является одной из задач математики как учебного предмета. Сегодня исследовательские умения относятся к ключевым компетенциям в системе образования.

Развитие исследовательских умений осуществляется в ходе выполнения заданий на конструирование задач с недостаточными данными и с заданным требованием.

Рассмотрим задачу, «работающую» на развитие исследовательских умений:

Задача 8.

Дана равнобедренная трапеция, основания которой 14 см и 8 см. Введите дополнительные данные, которые позволят найти боковую сторону трапеции.

Условие задачи можно дополнить не только числовыми, но и количественными данными. Можно намеренно дополнить задачу таким образом, чтобы это привело к несуществующей фигуре.

Например, дополнение: диагональ делит трапецию на два треугольника, один из которых – равнобедренный.

Ситуации 1 и 5 позволяют получить численный ответ, ситуации 2, 3, 4 приводят к выводу о несуществовании фигуры.

Задачи такого типа служат средством организации исследовательской деятельности, т.к. предполагают не только поиск собственно дополнений, но и их применение, и анализ каждого случая.

Требования ФГОС предусматривают формирование метапредметных результатов. На уроках математики этой цели могут служить межпредметные задачи, в которых не только условие и заключение, но и решение и обоснование требуют наличия знаний из других предметных областей.

Приведём пример такой задачи.

Задача 9.

В каком году началась перестройка Сампсониевской церкви в Петербурге в каменный Сампсониевский собор, если цифра десятков – наименьшее простое число, а число единиц – его куб?

Чтобы решить данную задачу недостаточно только знаний из предметной области «математика», т.к. в качестве ответа будет названо число 28.

Для решения задачи требуется привлечение знаний из других предметных областей, например, из истории:

- время основания Петербурга;

- историческое событие, связанное с возведением собора.

Задача, таким образом, связывает математические знания и исторические, культурные.

Успех обучения математике напрямую зависит от степени сформированности учебной мотивации обучающихся. Широкое использование в учебном процессе мотивационной функции задач является одним из средств его активизации. Такое применение задач способствует осознанному восприятию обучающимися программного материала, овладению прочными знаниями, развитию мыслительной деятельности школьников. Использование в обучении математике мотивационной функции задач означает, что они могут иметь своей дидактической целью:

• обоснование полезности и необходимости изучения того или иного теоретического материала;

• подготовку к введению новых понятий;

• ознакомление с конкретными моделями абстрактной теории;

• аргументацию целесообразности определений понятий;

• выявление некоторых свойств известных математических объектов;

• установление связей изученной теории с новой;

• подготовку к доказательству сложных предложений;

• ознакомление с новым методом решения задач;

• сравнение эффективности различных методов решения одной и той же задачи.

Несомненную ценность для мотивации изучения нового математического материала представляют задачи с практическим содержанием. Жизненной необходимостью решения подобных задач наиболее естественно обосновывать потребность в новых математических идеях, знаниях, методах. Акцентирование внимания на необходимости овладения математической теорией под влиянием потребностей практики способствует формированию у школьников научных взглядов. Использование задач для мотивации знаний, умений, методов создает условия для реализации на этапе введения нового учебного материала межпредметных связей, связи обучения математике с жизнью.

Предварение изучения математической теории постановкой задач предоставляет учителю благоприятные возможности для использования на уроках элементов проблемного обучения. Значимость задач проблемного характера для достижения образовательных, развивающих, воспитательных и практических целей обучения математике переоценить невозможно. Такие задачи могут не только служить средством введения новых понятий и методов, обоснования полезности изучения программного материала. Их использование обеспечивает более осознанное овладение математической теорией, учит школьников самостоятельному выполнению учебных заданий, приемам поиска, исследования и доказательства, основным мыслительным операциям, выделению существенных свойств математических объектов, формирует интерес к предмету. Использование элементов проблемного обучения ставит учеников в условия, вызывающие у них мышление, способное не только автоматически применять заученное, но и открывать для себя новое.

Задачи, используемые для подготовки обучающихся к изучению математической теории, следует подбирать так, чтобы их постановка привела не только к необходимости приобретения новых знаний и умений, но и к применению приобретенных знаний для решения не только поставленной задачи, но и других практических задач.

Рассмотрим пример использования задач для мотивации необходимости овладения новой математической теорией (введение понятия линейной функции).

Задача 10.

Основной месячный заработок рабочего сельскохозяйственного предприятия - 760 рублей. За производство сверхплановой продукции стоимостью в один рубль ему дополнительно выплачивается 19 копеек. Выясните вид зависимости общего месячного заработка рабочего от стоимости произведенной им сверхплановой продукции.

Первоначально необходимо разъяснить обучающимся смысл экономических терминов «сверхплановая продукция», «дополнительная оплата труда», «стоимость продукции», после чего решение задачи осуществляется учениками под руководством учителя.

Применение графического метода к решению текстовых задач на движение и на работу

К числу наиболее сложных заданий школьного курса математики по праву можно отнести текстовые задачи и в особенности задачи с практико-ориентированным содержанием. Среди них можно выделить задачи с одной величиной и задачи на процессы, в которых речь идет о связи между величинами (скорость – время – путь; производительность – время – работа; цена – количество – стоимость; урожайность – площадь поля – урожай; …). В процессе вступительных испытаний абитуриентам чаще всего предлагаются задачи на работу и на движение, которые традиционно решаются либо арифметическим (по действиям), либо алгебраическим (с использованием уравнений, неравенств, их систем) способом. Но можно выделить блок таких задач, при решении которых целесообразно воспользоваться графиком равномерного движения и свойствами геометрических фигур. В этих задачах идет речь о некотором взаимодействии – одновременно выполняемой работе или движении нескольких объектов. В качестве демонстрации преимущества геометрического метода рассмотрим следующую задачу.

Задача 1. Два автобуса выехали одновременно из пунктов А и В навстречу друг другу с постоянными и неравными скоростями. Они встретились на расстоянии 65 км от пункта В. Через 2 часа 30 минут после встречи второй автобус, миновав пункт А, находился в 30 км от него, а первый в это время, миновав пункт В, находился от второго автобуса на расстоянии в два раза большем, чем расстояние между пунктами А и В. Найдите скорость (в км/ч) второго автобуса.

Рассмотрим алгебраический способ решения этой задачи. Составим таблицу. Обозначим через х км/ч и у км/ч соответственно скорости первого и второго автобусов. Тогда, если принять длину всего пути между пунктами А и В за S км, то время, через которое они встретились, равно 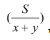ч. При этом первый автобус проехал (S – 65) км, а второй – 65 км:

Составим систему уравнений, используя полученные таблицы:

Попробуем рассмотреть эту же задачу в контексте прямоугольной системы координат, приняв ось абсцисс за ось времени, а ось ординат – за ось преодоленного пути. Напомним, что график равномерного движения представляет собой график линейной зависимости, то есть, графиком является прямая. Точка пересечения двух прямых в контексте задачи – это момент нахождения автобусов в одной точке, то есть момент встречи. В итоге при использовании в качестве модели задачи изображения в одной системе координат графиков движения каждого из автобусов появляется, прежде всего, наглядное представление о предложенной ситуации:

Принимая во внимание лаконичность, краткость и наглядность решения задач с помощью графического метода, остановимся на нем подробнее.

Прежде всего, рассмотрим две опорные геометрические конструкции.

Эти две геометрические конструкции чаще всего встречаются при использовании графического метода решения текстовых задач на работу и на движение.

Выделим еще несколько ситуаций, которые можно рассмотреть в качестве типовых задач.

Задача 2.1. (Типовая задача 1) Из пунктов А и В навстречу друг другу направились с постоянными скоростями два пешехода. После встречи первый пешеход через 36 минут прибыл в пункт В, а второй пешеход через 25 минут прибыл в пункт А. Сколько времени был в пути каждый из пешеходов?

Решение:

Изобразим графики движения пешеходов в прямоугольной системе координат.

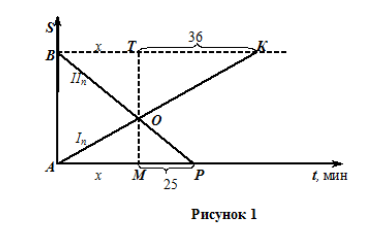
Примем за х минут время, через которое с момента начала движения пешеходы встретились. Воспользовавшись первым признаком подобия, имеем (конструкция №1):

30 + 36 = 76 (мин); 30 + 25 = 55 (мин).

Ответ: 1ч16мин, 55мин.

Абсолютно аналогичное решение имеет следующая задача на работу.

Задача 2.2. Два кондитера должны испечь коржи для двух одинаковых тортов. После того момента, как из коржей одного и другого кондитеров уже можно было сложить целый торт, первый еще трудился 36 минут, а второй – 25 минут. За какое время каждый из них справился с работой?

Решение:

Изобразим графики зависимости выполненной работы от времени в прямоугольной системе координат. В данном случае ось ординат совпадает с осью выполненной работы. При этом отрезок ОВ соответствует одному испеченному торту.

Примем за х минут время, через которое с момента начала работы кондитеры совместно испекли столько коржей, сколько необходимо для одного торта. Воспользовавшись первым признаком подобия, имеем:

30 + 36 = 76 (мин); 30 + 25 = 55 (мин).

Ответ: 1ч16мин, 55мин.

Если в предыдущих задачах два объекта двигались навстречу друг другу или рассматривалась совместная работа, то отличительной особенностью второй типовой задачи является движение в одном направлении или параллельное выполнение одинакового объема работ, но о совместной работе речь не идет.

Задача 3.1. (Типовая задача 2) Из города А в город В, расстояние между которыми 100 километров, одновременно выехали автомобиль и мотоцикл. Когда автомобиль проехал 51 километр, мотоциклу оставалось ехать 26 километров. Сколько километров останется проехать автомобилю, когда мотоцикл доберется до города В?

Решение:

Изобразим графики движения автомобиля и мотоцикла в прямоугольной системе координат.

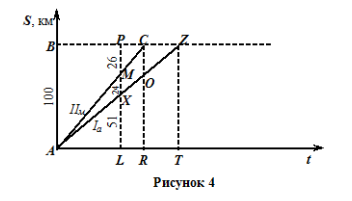
Используя первый признак подобия, имеем (конструкция №2)

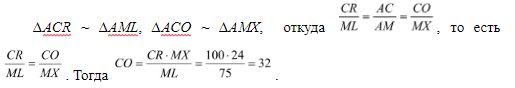
Ответ: 32 км.

Задача на работу в этом случае могла быть, например, такой.

Задача 3.2. Двум машинисткам необходимо набрать по 100 страниц текста. Они приступили к работе одновременно. Когда первая набрала 51 страницу, второй оставалось набрать 26 страниц. Сколько страниц останется набрать первой машинистке, когда вторая закончит работу?

Решение:

Изобразим графики зависимости выполненной работы от времени в прямоугольной системе координат. При этом отрезок АВ соответствует всей выполненной работе, то есть ста набранным страницам.

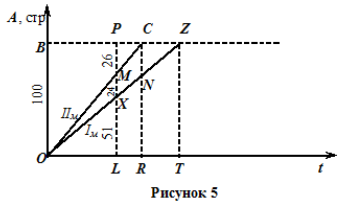
Используя первый признак подобия, имеем

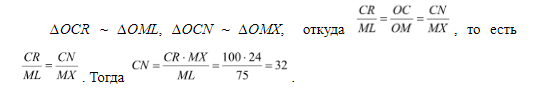
Ответ: 32 стр.

Иногда в задачах речь идет сразу о трех объектах, а, значит, для иллюстрации ситуации в прямоугольной системе координат выполняется построение уже трех прямых.

Задача 4.1. (Типовая задача 3) Три пешехода идут в одном направлении с постоянными скоростями. Когда 1-ый и 2-ой находились в одной точке, 3-ий отставал от них на 150 метров. Когда 3-ий догнал 1-го, 2-ой отставал от них на 100 метров. Найдите расстояние (в метрах) между 1-ым и 2-ым в тот момент, когда 3-ий и 2-ой находились в одной точке.

Решение:

Воспользуемся прямоугольной системой координат. Примем за начальный момент времени – нахождение в одной точке 1-го и 2-го пешеходов (3-ий позади на 150м).

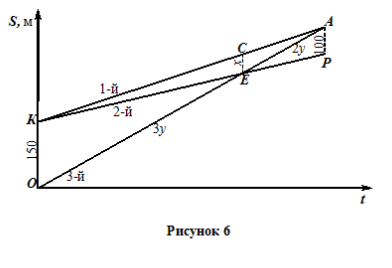
Пусть x м – расстояние между 1-ым и 2-ым в тот момент, когда 3-ий и 2-ой находились в одной точке. Тогда, воспользовавшись первым признаком подобия, имеем:

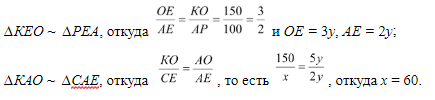
Ответ: 60 м.

Задача на работу в этом случае могла бы выглядеть так:

Задача 4.1. Два станка изготовили по 150 деталей к тому моменту, как начал работу 3-й станок. Когда совпадало количество изготовленных деталей у 3-го и 1-го станков, 2-ой отставал от них на 100 деталей. Найдите на сколько деталей изготовил больше 1-ый станок в тот момент, когда 3-ий и 2-ой станки изготовили одинаковое количество деталей.

Решение:

Рассмотрим задачу в контексте прямоугольной системы координат. Примем за начальный момент времени – вступление в работу 3-го станка (1-й и 2-й уже изготовили по 150деталей).

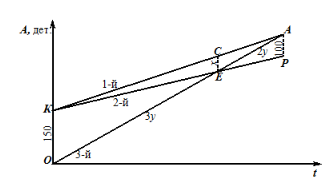
Рисунок 7

Пусть на x дет. больше изготовил 1-ый станок в тот момент, когда 3-ий и 2-ой станки изготовили одинаковое количество деталей. Тогда, воспользовавшись первым признаком подобия, имеем:

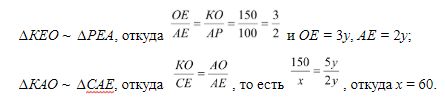
Ответ: 60 дет.

Иногда в задаче может идти речь о движении с возвращением. В этом случае при одинаковой скорости движущегося объекта график представляет собой равнобедренный треугольник. В связи с этим рассмотрим еще одну типовую задачу.

Задача 5. (Типовая задача 4) Через полчаса после того, как Дима вышел из дому в школу, вслед за ним вышел его старший брат Вова (работающий во вторую смену), который догнал Диму, передал ему забытый завтрак и тут же пошел обратно с прежней скоростью. Сколько времени потратил на весь путь Дима, если известно, что Вова вернулся домой в тот момент, когда Дима подошел к школе, и скорость Вовы в 1,5 раза больше скорости Димы?

Решение:

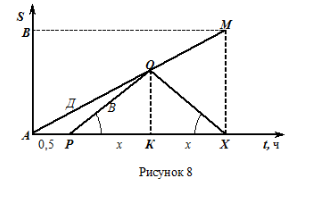
Пусть х ч потратил Вова для того, чтобы догнать Диму. Тогда, с учетом того, что ∆РОХ равнобедренный, имеем РК = КХ = х.

Поскольку при заданном расстоянии скорость обратно пропорциональна потраченному времени, то приняв во внимание расстояние, которое прошел

Ответ: 2,5ч.

Задачу на работу, аналогичную задаче на движение с возвращением, не имеет смысла рассматривать, поскольку такие задачи в математических сборниках не встречаются. Да и вести речь о результатах труда, которые уничтожаются, прежде всего, не разумно.

Рассмотрим еще несколько задач, перекликающихся в некоторой степени с типовыми задачами, но при этом имеющих некоторые существенные отличия.

Задача 6. Из двух городов А и С, расстояние между которыми равно 90км, навстречу друг другу направились грузовик (из А) и скутер (из С). Одновременно из города В, находящегося на расстоянии 10км от города С (город С находится между городами А и В) в город А выехал автомобиль. Через сколько минут встретились грузовик и скутер, если известно, что это произошло через 30 минут после того, как автомобиль догнал скутер, а грузовик до встречи с автомобилем провел в пути в два раза больше времени, чем скутер до того, как его догнал автомобиль?

Решение:

Построим в прямоугольной системе координат графики движения автомобиля, грузовика и скутера. Отметим на рисунке все числовые данные задачи.

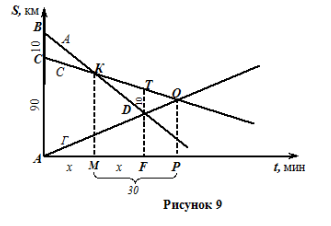
Пусть х минут прошло с момента начала движения до момента, когда автомобиль догнал скутер.

По теореме Фалеса СК = КТ, ВК = КD, откуда ∆СВК = ∆ТDК по двум сторонам и углу между ними. Тогда, ТD = ВС = 10.

Воспользовавшись первым признаком подобия, имеем:

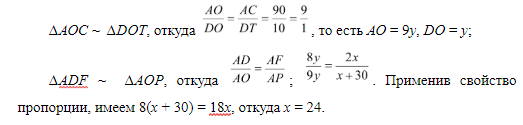
Тогда до встречи грузовика и скутера прошло 24 + 30 = 54 (мин).

Ответ: 54 мин.

Задача 7. Из пункта А в пункт В выехал грузовик, а через 15 минут, вслед за ним выехал автомобиль. Проехав половину пути от А до В автомобиль догнал грузовика. Когда автомобиль прибыл в пункт В, грузовику оставалось проехать еще третью часть всего пути. За какое время грузовик преодолел путь от А до В?

Решение:

Изобразим графики движения автомобиля и грузовика в прямоугольной системе координат.

Пусть за х минут автомобиль преодолел половину пути, равного S.

Тогда по теореме Фалеса АО = ОС, МО = ОК, откуда ∆АОМ =∆СOК и КС = АМ = 15.

Воспользовавшись первым признаком подобия, имеем:

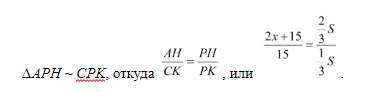
Упростив правую часть и воспользовавшись свойством пропорции, получаем 2х + 15 = 30, откуда х = 7,5.

АЕ = 2х + 30 = 15 + 30 = 45.

Ответ: 45 мин.

Задача 9. Пешеход и скутер отправились одновременно из пункта А в пункт В. В пункте В скутер повернул обратно и встретил пешехода через 1 час после начала движения. Не останавливаясь, скутер доехал до пункта А, снова развернулся и догнал пешехода через 40 минут после первой встречи. Найдите время (в часах), за которое пешеход пройдет расстояние от А до В.

 Решение:

Воспользуемся прямоугольной системой координат.

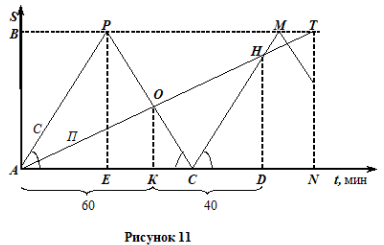
Ответ: 2,5 часа.

Таким образом, к числу задач, которые следует попробовать решить графическим методом, относятся задачи на движение нескольких объектов или на совместное (одновременное) выполнение работы. При этом, как правило, в рамках описанного процесса фигурирует в числовом выражении только одна величина: либо время, либо преодоленный путь (выполненная работа). Скорость или производительность в задаче могут быть упомянуты лишь в связи с понятием пропорциональности.

Список литературы:

1. Азаров А.И. Математика за курс базовой школы: обучение: экзамен: тестирование. – Минск: Аверсэв, 2006. – 480 с.: ил. – (Школьникам, абитуриентам, учащимся).
2. Азаров А.И., Булатов В.И., Романчик В.С., Шибут А.С. Математика: тематические тесты для подготовки к централизованному тестированию и экзамену. – Минск: Аверсэв, 2006. – 192с.: ил. – (школьникам, абитуриентам, учащимся).
3. Асмолов А. Г. и др. «Формирование УУД в основной школе: от действия к мысли». Система заданий. М. «Просвещение», 2010
4. Асмолов А.Г. Как проектировать универсальные учебные действия в школе: от действия к мысли: пособие для учителя. М.: Просвещение, 2008.
5. Астряб А.М. Наглядная геометрия. / А.М. Астряб – М.: Книга по Требованию, 2013. – 160 с.
6. Бруцкая О.А. Программа по математике в соответствии с требованиями ФГОС/ Первое сентября. 2014. № 6. [Электронный ресурс] – Режим доступа. – URL: http://festival.1septiber.ru/articles/627066/ (в открытом доступе).
7. Булынин В. Математика, № 14, 2005 с. 39 – 41, Применение графических методов при решении текстовых задач.
8. Блинова Т.Л. Современные аспекты методики обучения математике / Т. Л. Блинова, Э. А. Власова, И. Н. Семенова, А. В. Слепухин. – Екатеринбург, 2007. – 190 с.
9. Бабанский Ю. К. Оптимизация процесса обучения / Ю. К. Бабанский. –М., 1982. – 192 с.
10. Вавренчук Н.А. Формирование математической речи младших школьников. Сб. материалов Междунар. Науч.- практ. Конф., Брест, 15-17 мая 2007г
11. Вахрушев А.А., Горячев А.В., Данилов Д.Д., Бунеева Е.В., Чиндилова О.В., Козлова С.А. Программа личностного развития и формирования универсальных учебных действий у обучающихся на ступени начального образования (образовательная система «Школа 2100»). // Народное образование. – 2010. -№1.
12. Веременюк В.В.: Тренажер по математике для подготовки к централизованному тестированию и экзамену. – Минск: ТетраСистемс, 2007. – 176 с.
13. Груденов Я.И. Совершенствование методики работы учителя математики: Кн. для учителя / Я. И. Груденов. – М.: Просвещение, 1990. – 224 с.
14. Действующие учебники по математике для учащихся общеобразовательных учреждений.
15. Егерев В.К., Зайцев В.В., Кордемский Б.А. и другие. Сборник задач по математике для поступающих в вуз, учебное пособие. / под редакцией М. И. Сканави – Мн: Выш. шк., 1990 – 528 с.: ил.
16. Куимова Е. И., Куимова К. А., Титова Е. И. Функции задач в обучении математике // Молодой ученый. — 2014. — №12. — С. 280-281. — URL https://moluch.ru/archive/71/12175/ (дата обращения: 01.02.2018).
17. Крутецкий В.А. Психология математических способностей школьников/ Под редакцией Н.И. Чуприковой. М.: Издательство «Институт практической психологии»; Воронеж: Издательство НПО «МОДЭК», 1998. – 416 с.
18. Лабораторные и практические работы по методике преподавания математики: Учеб. пособие для студентов / Е. И. Лященко, К. В. Зобкова Т. Ф. Кириченко и др.; Под ред. Е.И. Лященко. – М.: Просвещение, 1988. –223 с.
19. Ложкина Е.М., Походова И.С. Введение в моделирование. Математические модели в естествознании (биология, химия, экология). – СПб: Изд-во РГПУ им. А.И. Герцена, 2009.
20. Литвиненко В.Н., Мордкович А.Г. Практикум по элементарной математике: Алгебра. Тригонометрия. 2-ое издание, переработанное и дополненное. М.: Просвещение, 1991 – 352 с.
21. Манвелов С. Г. Конструирование современного урока математики: кн. для учителя / С. Г. Манвелов. – М.: Просвещение, 2002. – 175 с.
22. Методика и технология обучения математике. Курс лекций: пособие для вузов / Н. Л. Стефанова, Н. С. Подходова и др. – М.: Дрофа, 2005. – 416 с.
23. Методика преподавания математики в средней школе. Общая методика: учеб. пособие для студ. физ.-мат. ф-тов пед. ин-тов / В. А. Оганесян. М. Колягин. – М.: Просвещение, 1980. – 368 с.
24. Методика преподавания математики в средней школе. Общая методика: учеб. пособие для студ. пед. ин-тов спец. 2104 Математика и 2105 Физика / А. Я. Блох, Е. С. Канин и др. – М.: Просвещение, 1985. – 336
25. Методика обучения математике: вопросы теории и практики. Учебное пособие для студентов. /Петрова А.И, Жирков Е.П, Аргунова Н.В, Макарова С.М, Ефремов В.П. Якутск: Издательско-полиграфический комплекс СВФУ, 2011. – 138 с.
26. Методика обучения математике в 2 ч. Часть 1: учебник для академического бакалавриата / Н. С. Подходова [и др.]; под ред. Н. С. Подходовой, В. И. Снегуровой. — М.: Издательство Юрайт, 2017. — 274 с.
27. Орлов. В.В. Геометрия в задачах: 7 – 9 класс. – СПб: Мир и семья – 95; Интерлайн, 1999.
28. Пойа Д. Математическое открытие. Решение задач: основные понятия, изучение и преподавание / Д. Пойа. – М.: Наука, 1976. – 448 с.
29. Репьев, В.В. Общая методика преподавания математики / В. В. Репьев. –М.: Учпедгиз, 1958. – 223 с.
30. Рубинштейн, С.Л. Основы общей психологии. Т.1. М.: Педагогика, 1989.
31. Рудин В.Н., Рудина Е.И. Графическое решение текстовых задач (пособие для учителей и школьников) / Издание Томского института повышения квалификации работников образования. 1995
32. Саранцев Г. И. Методика обучения математике в средней школе: учеб. пособие для студентов / Г. И. Саранцев. – М.: Просвещение, 2002. – 224 с.
33. Столяр А.А. Педагогика математики: Курс лекций / А. А. Столяр. – Минск: Выш. школа, 1974. – 382 с.
34. Селевко Г.К. Современные образовательные технологии. М.: 1998.
35. Современная методическая система математического образования: колл. монография / Н.С. Подходова [и др.]; под ред. Н.Л. Стефановой, Н.С. Подходовой, В.И. Снегуровой. – СПб: Изд-во РГПУ им. А.И. Герцена, 2009. – С. 24–27.
36. Шапиро И.М. Мотивационная функция задач в обучении математики / Сибирский межвузовский журнал «Педагог» http://www.altspu.ru/Journal/pedagog/pedagog_4/articl_12.html (дата обращения: 01.02.2018).
37. Эрдниев П.М., Теория и методика обучения математике в начальной школе. (педагогическая наука – реформе школы). – М.: Педагогика, 1988. -208с.