Методика применения свойства совпадения выражений по знаку для решения неравенств и уравнений

Умение решать задачи является одним из основных показателей уровня математического развития обучающихся, глубины освоения учебного материала. Если внимательно проанализировать содержание школьного курса математики, то можно увидеть, что он в основном состоит из теоретического обоснования способов решения различных видов задач. Поэтому естественно, что решению задач уделяется огромное внимание и значительное учебное время.

За время обучения в школе каждый ребенок решает огромное количество задач. При этом все обучающиеся решают одни и те же задачи, а в итоге некоторые ученики овладевают общим умением решения задач, а многие, встретившись с задачей незнакомого или малознакомого вида, теряются и не знают, как к ней подступиться.

Одной из причин этого явления является то, что одни обучающиеся вникают в процесс решения задач, стараются понять, в чем состоят приемы и методы решения задач, изучают задачи. Другие же не задумываются над этим, стараются лишь как можно быстрее решить заданные задачи. Эти обучающиеся не анализируют в должной степени решаемые задачи и не выделяют из решения общие приемы и способы. Задачи зачастую решаются лишь ради получения ответа. У большинства обучающихся достаточно смутные, а порой и неверные представления о сущности решения задач, о самих задачах. Как могут обучающиеся решить сложную задачу, если они не представляют, из чего складывается анализ задачи, как могут они решить задачу на доказательство, если они не знают, в чем смысл доказательства? Многие обучающиеся не знают, в чем смысл решения задач на построение, зачем и когда нужно производить проверку решения и т. д. Очевидно, что на таких представлениях не могут возникнуть сознательные и прочные умения в решении задач. Наблюдения показывают, что многие обучающиеся решают задачи лишь по образцу. А поэтому, встретившись с задачей незнакомого или мало знакомого вида, не знают, как к ней подступиться, с чего начать решение, и после нескольких неудачных попыток отказываются от этого, как они считают, безнадежного дела.

Для того чтобы научиться решать задачи, необходимо много поработать. Но эта работа не сводится лишь к решению большого числа задач. Если кратко обозначить то, что нужно сделать для этого, то можно так сказать: надо научиться такому подходу к задаче, при котором задача выступает как объект тщательного изучения, а ее решение — как объект конструирования и изобретения.

Д.А. Пойа отмечает: «Задача предполагает необходимость сознательного поиска соответствующего средства для достижения ясно видимой, но непосредственно недоступной цели. Решение задачи означает нахождение этого средства».

Процесс решения любой математической задачи может быть исследован с различных точек зрения:

• с математической – какова последовательность действий и как их надо совершить над данными задачи, чтобы найти искомое;

• с логической – устанавливается, из каких логических операций состоит процесс решения;

• с психологической – в чем состоят психологические особенности процесса решения задачи;

• с педагогической – определяются приемы, которые помогут ученику самостоятельно найти решение;

• с информационной – устанавливается возможность решения задачи с помощью компьютера.

Этапы работы над решением задачи

В процессе решения задачи целесообразно выделить четыре основных этапа:

Этап I. Анализ текста задачи.

Цель этапа:

• выделить объективное содержание задачи;

• выделить условие и заключение задачи;

• создать краткую запись задачи на искусственном языке, используя схемы, чертежа и т.д.

Как было указано выше, восприятие текста задачи зависит от субъективных факторов и личностного опыта, а также осложняется многозначностью языковых единиц. В ходе работы с текстом задачи, педагог должен помнить, что на основании этого текста существует три задачи:

• «задача», задуманная автором;

• «задача», которую воспринял обучающийся;

• «задача», которую воспринял учитель.

Сложность заключается в том, что не всегда эти «задачи» совпадают. В таком случае процесс решения задачи начинается с корректировки субъективного опыта, с приведения разных восприятий задачи к «общему знаменателю». Корректировка осуществляется посредством обучения языку математики. Чем младше ребёнок, тем выше субъективность его восприятия математического материала, поэтому на начальных этапах особенно важна работа с текстом задачи.

При реализации этого этапа важен самый первый момент — первоначальное чтение текста задачи, который часто недооценивается в школьной практике. Нередко ребенок не успевает даже прочесть текст, не то что осмыслить его, как учитель уже вызывает ученика к доске для решения задачи. Нужно отметить, что поспешный переход сразу по получении информации к ее преобразованию без предварительного анализа обедняет процесс познания. А вместе с тем внимательное предварительное прочтение текста, представление учеником ситуации, описанной в задаче, позволяет сделать много полезных выводов и предположений относительно подходов к ее решению. На данном этапе учат извлекать из текста информацию, определяющую решение задачи. Устанавливают, достаточно ли этой информации для решения, устраняют лишнюю информацию. Если этого требует сюжет задачи, то определяют реальность информации. Преобразуют текст задачи (либо по заданной схеме, либо для упрощения восприятия текста), оставляя только математически значимую информацию.

Анализ текста задачи

Обычно на этом этапе формируются два основных действия — чтение задачи и повторение текста задачи. При повторении текста задачи используют следующие приемы:

• абстрагирование числа от сюжета задачи;

• повторение задачи по логическим частям (этот прием используется на начальном этапе работы с задачей либо при повторении задачи с незнакомым сюжетом);

• повторение по структурным частям задачи;

• повторение полного текста задачи.

В зависимости от особенностей задачи, проводят математический, логический и семантический анализы текста задачи, используя следующие приемы:

• преобразование текста задачи, которое предполагает исключение из текста той части, которая не влияет на результат решения, либо дополнение текста задачи недостающими данными;

• изменение порядка слов или предложений;

• замена некоторых слов синонимами;

• замена содержательного описания термином или наоборот;

• дополнение текста пояснением; уточнение единиц измерения величин и др.

Текстовая модель задачи часто включает несущественную для решения информацию. Чтобы можно было работать только с существенными смысловыми единицами, текст задачи переводят на язык графических моделей, т.е. представляют текст с помощью невербальных средств — моделей различного вида: чертежа, схемы, графика, таблицы, символического рисунка и др.

Перевод текста на язык математики с помощью невербальных средств есть второй компонент общего приема решения задач и второй этап работы над задачей. Реализация этого этапа (второго компонента) предполагает выбор знаково-символических средств для построения графической модели, адекватной математическому содержанию задачи. Модель задачи, построенная по определенным правилам, есть аналог задачи, в котором более четко отражена структура связей и отношений между объектами либо величинами, описанными в сюжете задачи.

Перевод текста в форму графической модели позволяет обнаружить в нем свойства и отношения, которые часто с трудом выявляются при чтении. Рассмотрим примеры.

Задача 1.

Саша и Маша решили купить по одинаковому набору ёлочных украшений. Саше не хватило 1руб., а Маше 6 руб. Тогда ребята решили сложить вместе свои деньги и купить один набор игрушек на двоих, но им всё равно не хватило денег. Сколько денег было у каждого из ребят первоначально? Сколько стоил набор ёлочных украшений?

Данная задача во введении требует работы с текстом. Нужно обратить внимание на словосочетание «сколько-то денег не хватает», которое означает необходимость добавить денег, но не предполагает наличие денег само по себе, как зачастую кажется решающим.

Рассмотрим этап анализа текста задачи.

Задача 2.

Два грузовых автомобиля одновременно выезжают из пунктов А и Б навстречу друг другу. После встречи автомобиль, выехавший из пункта А прибывает в пункт В через два часа, а автомобиль, выехавший из пункта В прибывает в пункт А через 9/8 часа. Найдите скорость автомобилей, если расстояние между пунктами 210 км?

Данная задача на равномерное движение двух объектов, которое осуществляется навстречу друг другу. Структура текста задачи: У – Т – У (условие – требование – условие). Объекты – два автомобиля, выехавшие навстречу друг другу из пунктов А и В. Они начали движение одновременно и двигались до встречи одинаковое время. В условии не сказано, что изменялись скорости, следовательно, их движение на протяжение всего пути осуществлялось с постоянной скоростью. Первый автомобиль потратил на оставшуюся часть пути 2 часа. Это путь, который проделал второй автомобиль до встречи. Второй автомобиль потратил на оставшуюся часть пути 9/8 часа. Это путь, который проделал первый автомобиль до встречи. Путь, пройденный каждым автомобилем, составляет 210 км.

На основании выделенных в условии задачи данных можно сделать краткую запись условия и чертеж.

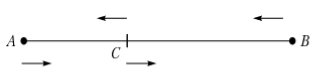
Также в результате собственно анализа текста можно получить и ответ задачи, если речь идёт о несуществовании объекта.

Этап II. Поиск решения задачи.

Цель этапа – составить план решения задачи, который может быть представлен устно или письменно, в виде текста, модели или поисковой схемы.

После того как текст задачи лаконично представлен в виде графической модели, следует перейти к анализу отношений и связей между известными значениями, а также между известными и неизвестными значениями величин. Для этого проводится детальный анализ этих отношений. Результат этого анализа позволяет выстроить план решения задачи.

Поиск плана решения задачи может быть реализован двумя путями:

• синтетическим;

• аналитическим.

Синтетический путь представляет путь от условия к заключению Основной вопрос: есть это, что из этого следует?

Примерные вопросы прямого анализа задачи:

• Прочитайте вопрос задачи. Можно ли сразу ответить на вопрос задачи?

• Охарактеризуйте задачу по составу. Какая она?

• Выделите первую простую задачу.

• Каким действием решается эта задача? Почему?

• Запишите решение первой простой задачи.

• Ответили ли мы на вопрос исходной задачи?

• Выделите вторую простую задачу.

• Каким действием будем решать эту задачу? Почему?

• Запишите решение второй простой задачи.

• Скажите ответ второй простой задачи.

• Ответили ли мы на вопрос исходной задачи?

• Скажите, по какому плану решается исходная задача.

Аналитический путь представляет путь от заключения к условию. Основной вопрос: что нужно знать/доказать/найти, чтобы получить это?

Примерные вопросы обратного анализа задачи:

• Прочитайте вопрос задачи.

• Можно ли сразу ответить на вопрос задачи?

• Каких два (три…) значения надо знать, чтобы ответить на вопрос задачи?

• Какое значение нам уже известно?

• Что неизвестно?

• Какие из этих значений мы знаем?

• Расскажите план решения задачи.

В педагогической практике чаще всего используется смешанный аналитико-синтетический путь: от заключения, но с учётом того, что имеется в условии.

Примерные вопросы смешанного анализа задачи:

• Можем ли мы сразу ответить на вопрос задачи? Почему?

• А можем ли узнать, сколько …? Почему?

• Расскажите план решения задачи.

Под поиском решения задачи Л.Л. Гурова понимает отыскание принципа построения логики решения в соответствии с чем выполняются те или иные действия, о которых нельзя сказать, приведут ли они к требуемому результату или нет.

Каждый анализ задачи завершается составлением плана решения задачи, после чего записывается само решение, что, собственно, и является следующим этапом работы над задачей.

Рассмотрим этап анализа и фрагмент поисковой схемы.

Задача 2.

Два грузовых автомобиля одновременно выезжают из пунктов А и Б навстречу друг другу. После встречи автомобиль, выехавший из пункта А прибывает в пункт В через два часа, а автомобиль, выехавший из пункта В прибывает в пункт А через 9/8 часа. Найдите скорость автомобилей, если расстояние между пунктами 210 км?

Для поиска и составления плана решения продолжим анализировать и получать следствия из условия задачи. Было установлено, что до встречи автомобили двигались одинаковое время t1AC=t2BC. Известно время, которое они потратили на путь после встречи, известно расстояние АВ. Имеющиеся связи отразим схематично:

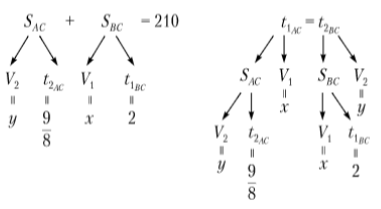
На этапе ознакомления учащихся со схемой поиска можно предложить им следующие задания: посмотреть на данные схемы и объяснить закономерности, которые были положены в основу их создания.

Из анализа структуры текста задачи (У – Т – У) и приведенных схем становится понятно, что решать задачу мы можем, составив схему уравнений, выразив в качестве переменных скорости автомобилей.

Этап III. Реализация плана решения и его обоснование.

Если на втором этапе была составлена схема, то на третьем этапе, мы получаем план решения задачи, двигаясь по схеме снизу верх.

 Необходимо обратить внимание, что при решении геометрических задач целесообразно вести запись решения в два столбика: в левом записывать шаги решения, в правом – их обоснование. Задачи в таком случае будут служить средством обучения логическому обоснованию.

Рассмотрим этап реализации плана решения задачи 2.

Пусть х км/ч – скорость первого автомобиля, тогда у км/ч – скорость второго автомобиля, тогда получаем два уравнения:

1) 9/8у +2х = 210

2) 9/8у : х = 2х : у

После составления уравнений целесообразно обратиться к схемам и проследить процесс составления каждого уравнения.

Учащиеся объединяют составленные уравнения в систему и решают ее.

Этап IV. Исследование, проверка решения задачи и запись ответа.

Сущность проверки заключается в формулировании заключений по тексту задачи с выполнением арифметических действий или без них. Этот вид проверки носит неформальный характер, и сами рассуждения основаны на понимании проверяющим всех слов и соответствий, заданных в тексте задач. Четкого алгоритма проведения этой проверки не существует. Каждая задача требует особого хода рассуждений.

В рамках этого этапа может проводиться:

• смысловая проверка (существует ли объект);

• проверка на правильность (логических и математических операций);

• обобщение и систематизация полученного опыта;

• рефлексия;

• исследование задачи и поиск альтернативных методов и способов решения.

Проверку на существование объекта лучше сделать первым этапом или совместить с анализом, чтобы избавить себя от лишней работы.

Рассмотрим проверку решения задачи на примере задачи 2.

После решения системы уравнений обучающимся следует предложить проверить правильность решения методом подстановки.

Также на данном этапе можно познакомить учащихся с решающей моделью – математической, в частности, с ее структурой:

1. содержательная составляющая (компонент структуры)

2. объяснительная составляющая (объяснение того, что значит каждая буква или число в выражении).

Проверка решения системы не является полной проверкой задачи. Для проверки задачи учитель может использовать различные приемы:

• проверка задачи по смыслу;

• решение задачи другим способом;

• составление обратной задачи.

Рассмотрим еще один пример.

Задача 3.

На книжной полке стоит двухтомник с толщиной страницы 0,05 мм и обложки 1 мм. В первом томе 320 страниц, во втором – 400. Жучок прогрыз обе книги от первой страницы первого тома до последней страницы второго. Какое расстояние он при этом преодолел?

Задача предполагает, казалось бы, одно решение. Но находятся учащиеся, которые выдвигают версию, что книги могли быть поставлены вверх ногами, и тогда получаются альтернативные ответы.

При решении задач на построение можно совместить этап исследования и этап анализа в отношении исследования количества потенциально возможных случаев.

Некоторые авторы считают нецелесообразным предлагать обучающимся задачи с многозначными или неопределёнными ответами, как и задачи с несуществующими объектами. Тем не менее, задачи такого плана готовят ребёнка к таким жизненным ситуациям и проблемам, решение которых неизвестно или невозможно на данный момент. Такие задачи предполагают критический исследовательский подход.

Необходимо отметить, что вышеперечисленные этапы взаимно переплетены, и решающий может многократно возвращаться к ним. У учеников следует воспитывать потребность в выполнении всех четырёх этапов.

Рассмотрим различные подходы к решению дробно-рациональных неравенств и уравнений.

Общеизвестным методом решения дробно-рациональных неравенств школьного курса математики является метод интервалов, который можно описать следующим алгоритмом:

1. Преобразование неравенства к соответствующему виду (справа 0; числитель и знаменатель левой части представлены в виде произведения без повторов линейных множителей в стандартном виде или их степеней);

2. Рассмотрение функции, соответствующей левой части неравенства;

3. Нахождение области определения функции;

4. Нахождение нулей функции;

5. Изображение на координатной прямой области определения и нулей функции;

6. Расстановка знаков с учетом четности кратных множителей (удобно над точками, соответствующими множителям, которые вошли в неравенство в четной степени или под знаком модуля, ставить «галочку», означающую отсутствие чередования знаков при переходе через рассматриваемую точку);

7. Нахождение решения неравенства (не забыть про изолированные точки, которые на координатной прямой изображены закрашенными, но не в один из промежутков решения не вошли).

Решение неравенств, содержащих переменную под знаком модуля, опирается на определение понятия «модуль» (модуль – это расстояние на числовой прямой от начала координат до числа, записанного под знаком модуля) и требует глубокого понимания этого понятия.

Неравенства, содержащие переменную под знаком корня или в показателе степени, а также логарифмические неравенства при решении предполагают использование свойств соответствующих функций и относятся к числу наиболее сложных заданий в рамках этой содержательной линии предмета «Математика».

При этом наибольший интерес при решении неравенств любого вида (как и при решении вообще любых заданий) представляют те приемы и методы, которые позволяют максимально просто, быстро и точно дать ответ на поставленный вопрос. В случае рассмотрения темы «Неравенства» — это использование теорем о совпадающих по знаку выражениях, которые позволяют рационализировать ход решения неравенств, содержащих переменную под знаком модуля, корня, логарифма или в показателе степени, сводя эти неравенства к легко решаемым методом интервалов дробно-рациональным неравенствам. Речь идет о применении следующих четырех теорем:

Что и требовалось доказать.

Что и требовалось доказать.

Разберемся, как применяются все четыре теоремы при решении неравенств различных видов.

Начнем с неравенств, содержащих переменную под знаком модуля.

Пример 1.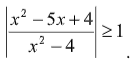

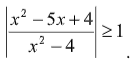
Аналогично для второго неравенства получаем

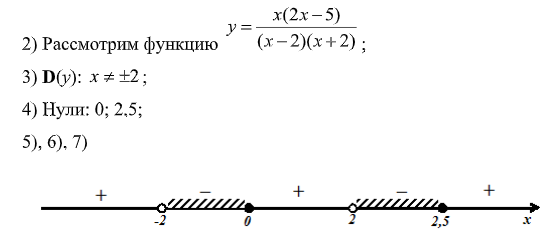
Объединяя два полученных решения, делаем общий вывод:

Рассмотрим еще несколько неравенств, при решении которых применима первая теорема.

Пример 2.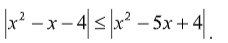

Решение:

Традиционно это неравенство преобразуется в систему неравенств, каждое из которых надо решить и в итоге найти пересечение решений.

Перенесем модуль из правой части в левую и применим Т1.

Разделим левую и правую части неравенства на (-8) (не забыв поменять знак неравенства) и применим метод интервалов.

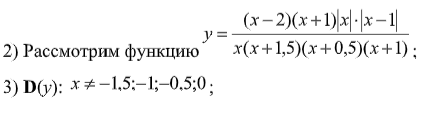
4) Нули: 1; 2 (напомним, что нулями являются только внутренние точки области определения, поэтому числа -1 и 0 к нулям не относятся);

5), 6), 7)

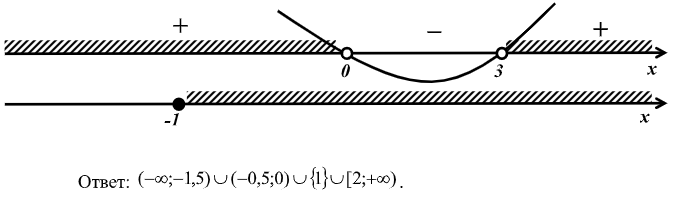
Таким образом, можно выделить отличительный признак неравенств, которые целесообразно попытать решить с использованием первой теоремы о совпадающих по знаку выражениях – неравенство содержит множитель, от которого зависит знак при сравнении с нулем, и который представляет собой либо разность модулей двух выражений с переменной, либо разность модуля выражения с переменной и некоторого числа.

Очевидно, вторая теорема применяется, прежде всего, при наличии разности двух корней, хотя бы один из которых содержит переменную в подкоренном выражении.

Можно выделить несколько простейших ситуаций, для которых нельзя сказать, что использование Т2 является более рациональным, чем стандартный подход:

Рассмотрим соответствующий пример.

Пример 6.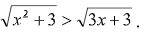

Решение (1-ый способ):

Возведя левую и правую части неравенства в квадрат, с учетом области допустимых значений имеем:

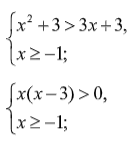
Решим первое неравенство методом парабол (используется алгоритм нахождения промежутков знакопостоянства квадратичной функции) и найдем пересечение двух множеств решений.

Далее решение совпадает с решением первым способом.

Но есть среди неравенств, содержащих переменную под знаком корня, неравенства, для которых использование второй теоремы о совпадающих по знаку выражениях все же рационализирует процесс решения. Рассмотрим несколько таких примеров.

Пример7.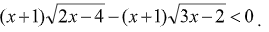

Решение:

Вынесем за скобки общий множитель и с учетом области допустимых значений применим Т2:

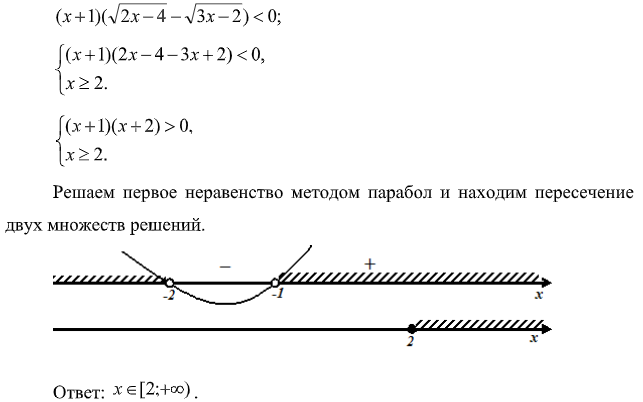
Решение рассмотренного выше неравенства сразу методом интервалов без использования теоремы о совпадающих по знаку выражениях более громоздко и требует больших временных затрат.

Пример8.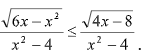

Решение:

Перенесем дробь из правой части неравенства в левую и с учетом области допустимых значений применим Т2:

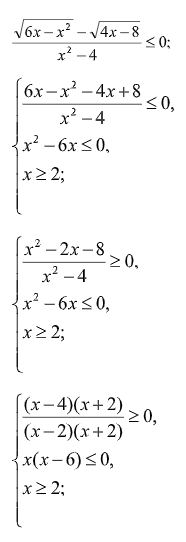
Решаем первое неравенство методом интервалов, второе методом парабол и находим пересечение трех множеств решений.

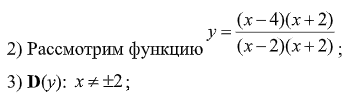
4) Нули: 4 (напомним, что нулями являются только внутренние точки области определения, поэтому число -2 к нулям не относится);

5); 6); 7)

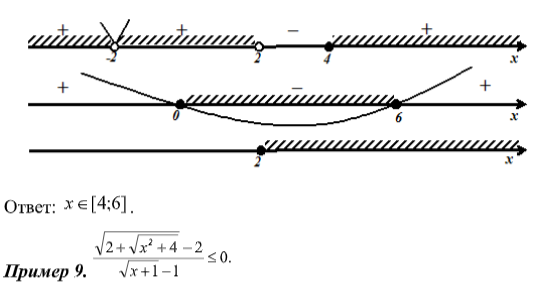
Решение:

Внесем под знак радикала число 2 в числителе и число 1 в знаменателе и с учетом области допустимых значений применим Т2 дважды для числителя и один раз для знаменателя:

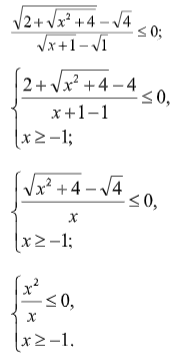
Решаем первое неравенство методом интервалов (помним, что сокращать на линейный множитель нельзя, поскольку в этом случае меняется область допустимых значений) и находим пересечение двух множеств решений.

Рассмотрим неравенство более высокого уровня сложности. При его решении можно применить сразу две теоремы о совпадающих по знаку выражениях.

Решим полученное дробно-рациональное неравенство методом интервалов.

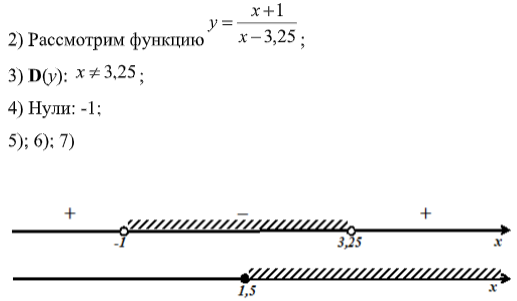
Ответ:[1,5;3,25)

Таким образом, отличительной особенностью неравенств, которые целесообразно попытать решить с использованием второй теоремы о совпадающих по знаку выражениях, является наличие в неравенстве множителя, от которого зависит знак при сравнении с нулем, и который представляет собой либо разность корней из двух выражений с переменной, либо разность корня из выражения с переменной и некоторого числа.

Третья теорема применяется при наличии разности, содержащей переменную в показателях степеней. Следует отметить, что ее можно рассматривать как альтернативный вариант традиционному подходу даже при рассмотрении простейших неравенств.

Поскольку основание меньше единицы при переходе к показателям степеней не забываем поменять знак неравенства:

Очевидно, применение третьей теоремы о совпадающих по знаку выражениях обходит необходимость сравнивать основание степени с единицей при переходе к показателям степеней. Это, безусловно, может помочь избежать ошибок по невнимательности.

Рассмотрим еще несколько неравенств, содержащих переменную в показателе степени, для которых применение Т3 гораздо эффективнее традиционного подхода.

Пример 12.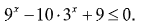

Решение:

Выполним временную замену переменной для разложения левой части неравенства на множители:

Решение:

Заменим все вычитаемые на степени с соответствующими показателями и применим Т3:

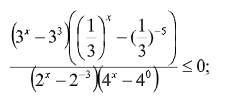
К числу неравенств повышенного уровня сложности можно отнести по праву показательно-степенные неравенства, то есть неравенства, в которых переменная содержится и в основании, и в показателе степени. Традиционно такие неравенства решаются посредством рассмотрения двух случаев: основание меньше единицы и основание больше единицы. А это уже двойной объем работы. При использовании же третьей теоремы о совпадающих по знаку выражениях решение ограничивается одним случаем и является посильным для учащихся даже среднего уровня обученности.

Пример 14.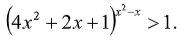

Решение:

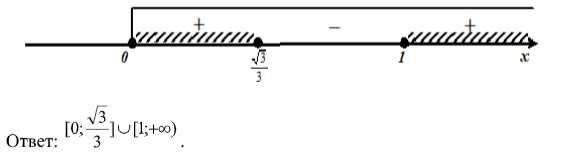
В итоге отличительной особенностью неравенств, которые целесообразно решать с использованием третьей теоремы о совпадающих по знаку выражениях, является наличие в неравенстве множителя, от которого зависит знак при сравнении с нулем, и который представляет собой либо разность двух показательных выражений с переменной в показателе, либо разность степени с переменной в показателе и некоторого числа.

Очевидно, четвертая теорема применима в случае наличия разности, содержащей переменную под знаком логарифма (либо в основании логарифма). Эту теорему можно, как и Т3, рассматривать как альтернативный вариант традиционному подходу при рассмотрении простейших неравенств.

Первое и третье неравенства системы решаем методом парабол и находим пересечение трех множеств:

Далее решение совпадает с решение первым способом. Снова отметим, что применение теоремы о совпадающих по знаку выражениях обходит необходимость сравнивать основание логарифма с единицей при переходе к подлогарифмическим выражениям.

Рассмотрим еще несколько неравенств, содержащих переменную под знаком логарифма, для которых применение Т4 гораздо эффективнее традиционного подхода.

Пример 17.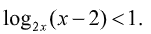

Решение:

Традиционно решение этого неравенства предусматривает рассмотрение двух случаев: основание больше единицы и основание меньше единицы, что требует немалых временных затрат.

Решение:

Рассмотрев числитель неравенства как квадратный трехчлен относительно логарифма, разложим его на множители:

Решим это неравенство методом интервалов и с учетом области допустимых значений найдем пересечение двух множеств.

4) Нули: 0 (помним, что нулями функции могут быть только внутренние точки области определения функции);

5); 6); 7)

Эти же четыре теоремы могут быть применены при решении некоторых уравнений. Рассмотрим сначала уравнения, в которых используется одна из теорем.

Рассматриваемому условию удовлетворяет только число 1.

Решение:

Область допустимых значений уравнения:x=>2.5 Пользуясь Т2, получаем:

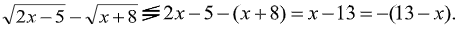
Тогда левая и правая части либо противоположны по знаку, либо одновременно равны нулю. Таким образом, равенство возможно, только если x – 13 = 0, откуда x = 13, что удовлетворяет области допустимых значений.

Ответ: 13.

Пример 23.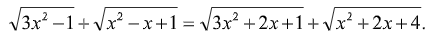

Решение:

При классическом подходе это уравнение имеет довольно громоздкое решение, связанное с домножением на сопряженные выражения. Для того, чтобы воспользоваться предлагаемым подходом, преобразуем уравнение в равенство двух разностей (для группировки слагаемых в качестве ориентира выбираем равенство коэффициентов при x2):

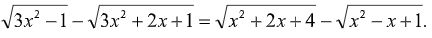
Заметим, что в некоторых уравнениях, как и в данном, имеет смысл не находить область допустимых значений, а для найденных значений переменной выполнять проверку.

Тогда по Т2:

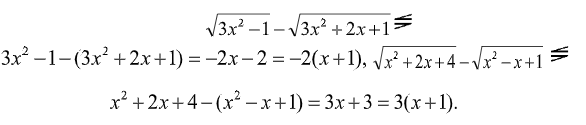
Тогда левая и правая части либо противоположны по знаку, либо одновременно равны нулю. Таким образом, равенство возможно, только если x + 1 =0 или x = -1. Проверка показывает, что найденное значение является корнем исходного уравнения.

Ответ: -1.

Пример 24. Найдите сумму квадратов корней уравнения

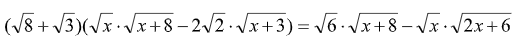
Решение:

Область допустимых значений данного уравнения: x=>0

Уравнение может быть преобразовано к виду:

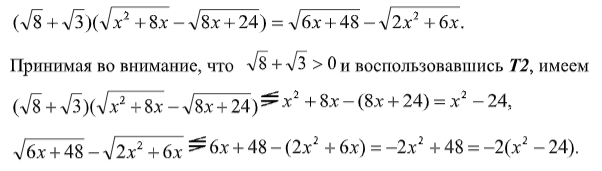
Тогда левая и правая части либо противоположны по знаку, либо одновременно равны нулю. Таким образом, равенство возможно, только если откуда с учетом ОДЗ . Тогда требуемая по условию сумма квадратов корней равна 24.

Ответ: 24.

Пример 25.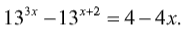

Решение:

Воспользуемся Т3 для левой части уравнения:

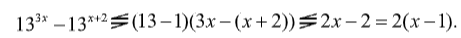
Тогда с учетом того, что 4 – 4x = –4(x – 1), левая и правая части либо противоположны по знаку, либо одновременно равны нулю. Таким образом, равенство возможно, только если x – 1 = 0, откуда x = 1.

Ответ: 1.

Пример 26.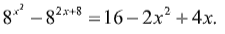

Решение:

Воспользуемся Т3 для левой части уравнения:

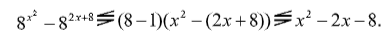
Тогда с учетом того, что 16 – 2x2 + 4x = –2(x2 – 2x – 8), левая и правая части либо противоположны по знаку, либо одновременно равны нулю. Таким образом, равенство возможно, только если откуда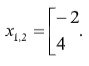

Ответ: -2; 4.

Тогда с учетом того, что 15 – 5x = –5(x – 3), левая и правая части либо противоположны по знаку, либо одновременно равны нулю. Таким образом, равенство возможно, только если x – 3 = 0, откуда x = 3.

Ответ: 3.

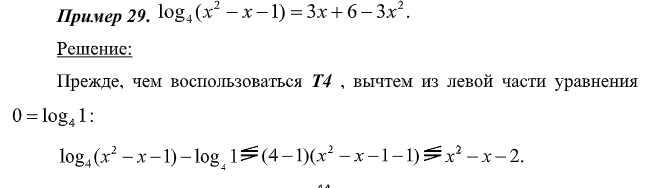
Тогда с учетом того, что 3x + 6x – 3x2 = –3(x2 – x – 2), левая и правая части либо противоположны по знаку, либо одновременно равны нулю. Таким образом, равенство возможно, только если откуда 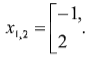Проверка показывает, что оба найденных значения являются корнями уравнения.

Ответ: -1; 2.

Помимо уравнений, в которых применима одна из четырех теорем, в некоторых ситуациях можно применить сразу две, три и даже все четыре теоремы.

Тогда можем воспользоваться Т2 и Т3 соответственно для левой и правой частей уравнения:

Решение:

Воспользуемся Т3 и Т1 отдельно для левой и правой частей уравнения соответственно:

<p Решение:

Область допустимых значений: x > 0.

Предварительно преобразовав правую часть уравнения в разность логарифмов, воспользуемся Т2 и Т4 отдельно для левой и правой частей уравнения соответственно:

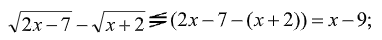
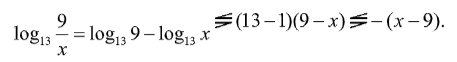
Тогда левая и правая части либо противоположны по знаку, либо одновременно равны нулю. Таким образом, равенство возможно, только если x – 9 = 0, откуда x = 9, что принадлежит области допустимых значений.

Ответ: 9.

Для правой части уравнения применим Т3 и Т2:

Ответ: 2.

Сформулируем обобщенный алгоритм действий при решении уравнения с использованием теорем о совпадающих по знаку выражениях:

1. убедиться в том, что левая или правая части уравнения (возможно, обе) представляют собой один из указанных ниже вариантов:

• разность квадратных корней или выражение, приводимое путем тождественных преобразований к такой разности;

• разность выражений, содержащих переменную под знаком модуля или выражение, приводимое путем тождественных преобразований к такой разности;

• разность степеней с одинаковым основанием или выражение, приводимое путем тождественных преобразований к такой разности;

• разность логарифмов с одинаковым основанием или выражение, приводимое путем тождественных преобразований к такой разности (возможен один логарифм, из которого всегда можно вычесть нуль, представляемый в виде логарифма);

2. воспользовавшись теоремами о совпадающих по знаку выражениях определить, с какими максимально упрощенными выражениями совпадают по знаку левая и правая части уравнения (или одна из них);

3. убедиться в том, что выражения, полученные для левой и правой частей уравнения, совпадают по модулю, но противоположны по знаку;

4. сделать вывод о том, что равенство возможно, только если выражение, совпадающее по знаку с исходным (в левой или в правой части уравнения), равно нулю;

5. решить полученное уравнение;

6. выполнить проверку.

Следует отметить, что далеко не для каждого уравнения, содержащего указанные выше разности, будут применимы теоремы о совпадающих по знаку выражениях. Но поскольку метод достаточно прост в применении и позволяет достаточно быстро проверить, есть ли возможность им воспользоваться, то любое уравнение, подходящее по внешнему виду под ситуации, описанные в пункте 1 обобщенного алгоритма действий, прежде всего, имеет смысл попытаться решить с использованием теорем о совпадающих по знаку выражениях.

Список литературы:

1. Азаров А.И. Математика за курс базовой школы: обучение: экзамен: тестирование. – Минск: Аверсэв, 2006. – 480 с.: ил. – (Школьникам, абитуриентам, учащимся).
2. Азаров А.И., Булатов В.И., Романчик В.С., Шибут А.С. Математика: тематические тесты для подготовки к централизованному тестированию и экзамену. – Минск: Аверсэв, 2006. – 192с.: ил. – (школьникам, абитуриентам, учащимся).
3. Асмолов А. Г. и др. «Формирование УУД в основной школе: от действия к мысли». Система заданий. М. «Просвещение», 2010
4. Асмолов А.Г. Как проектировать универсальные учебные действия в школе: от действия к мысли: пособие для учителя. М.: Просвещение, 2008.
5. Астряб А.М. Наглядная геометрия. / А.М. Астряб – М.: Книга по Требованию, 2013. – 160 с.
6. Бруцкая О.А. Программа по математике в соответствии с требованиями ФГОС/ Первое сентября. 2014. № 6. [Электронный ресурс] – Режим доступа. – URL: http://festival.1septiber.ru/articles/627066/ (в открытом доступе).
7. Булынин В. Математика, № 14, 2005 с. 39 – 41, Применение графических методов при решении текстовых задач.
8. Блинова Т.Л. Современные аспекты методики обучения математике / Т. Л. Блинова, Э. А. Власова, И. Н. Семенова, А. В. Слепухин. – Екатеринбург, 2007. – 190 с.
9. Бабанский Ю. К. Оптимизация процесса обучения / Ю. К. Бабанский. –М., 1982. – 192 с.
10. Вавренчук Н.А. Формирование математической речи младших школьников. Сб. материалов Междунар. Науч.- практ. Конф., Брест, 15-17 мая 2007г
11. Вахрушев А.А., Горячев А.В., Данилов Д.Д., Бунеева Е.В., Чиндилова О.В., Козлова С.А. Программа личностного развития и формирования универсальных учебных действий у обучающихся на ступени начального образования (образовательная система «Школа 2100»). // Народное образование. – 2010. -№1.
12. Веременюк В.В.: Тренажер по математике для подготовки к централизованному тестированию и экзамену. – Минск: ТетраСистемс, 2007. – 176 с.
13. Груденов Я.И. Совершенствование методики работы учителя математики: Кн. для учителя / Я. И. Груденов. – М.: Просвещение, 1990. – 224 с.
14. Действующие учебники по математике для учащихся общеобразовательных учреждений.
15. Егерев В.К., Зайцев В.В., Кордемский Б.А. и другие. Сборник задач по математике для поступающих в вуз, учебное пособие. / под редакцией М. И. Сканави – Мн: Выш. шк., 1990 – 528 с.: ил.
16. Куимова Е. И., Куимова К. А., Титова Е. И. Функции задач в обучении математике // Молодой ученый. — 2014. — №12. — С. 280-281. — URL https://moluch.ru/archive/71/12175/ (дата обращения: 01.02.2018).
17. Крутецкий В.А. Психология математических способностей школьников/ Под редакцией Н.И. Чуприковой. М.: Издательство «Институт практической психологии»; Воронеж: Издательство НПО «МОДЭК», 1998. – 416 с.
18. Лабораторные и практические работы по методике преподавания математики: Учеб. пособие для студентов / Е. И. Лященко, К. В. Зобкова Т. Ф. Кириченко и др.; Под ред. Е.И. Лященко. – М.: Просвещение, 1988. –223 с.
19. Ложкина Е.М., Походова И.С. Введение в моделирование. Математические модели в естествознании (биология, химия, экология). – СПб: Изд-во РГПУ им. А.И. Герцена, 2009.
20. Литвиненко В.Н., Мордкович А.Г. Практикум по элементарной математике: Алгебра. Тригонометрия. 2-ое издание, переработанное и дополненное. М.: Просвещение, 1991 – 352 с.
21. Манвелов С. Г. Конструирование современного урока математики: кн. для учителя / С. Г. Манвелов. – М.: Просвещение, 2002. – 175 с.
22. Методика и технология обучения математике. Курс лекций: пособие для вузов / Н. Л. Стефанова, Н. С. Подходова и др. – М.: Дрофа, 2005. – 416 с.
23. Методика преподавания математики в средней школе. Общая методика: учеб. пособие для студ. физ.-мат. ф-тов пед. ин-тов / В. А. Оганесян. М. Колягин. – М.: Просвещение, 1980. – 368 с.
24. Методика преподавания математики в средней школе. Общая методика: учеб. пособие для студ. пед. ин-тов спец. 2104 Математика и 2105 Физика / А. Я. Блох, Е. С. Канин и др. – М.: Просвещение, 1985. – 336
25. Методика обучения математике: вопросы теории и практики. Учебное пособие для студентов. /Петрова А.И, Жирков Е.П, Аргунова Н.В, Макарова С.М, Ефремов В.П. Якутск: Издательско-полиграфический комплекс СВФУ, 2011. – 138 с.
26. Методика обучения математике в 2 ч. Часть 1: учебник для академического бакалавриата / Н. С. Подходова [и др.]; под ред. Н. С. Подходовой, В. И. Снегуровой. — М.: Издательство Юрайт, 2017. — 274 с.
27. Орлов. В.В. Геометрия в задачах: 7 – 9 класс. – СПб: Мир и семья – 95; Интерлайн, 1999.
28. Пойа Д. Математическое открытие. Решение задач: основные понятия, изучение и преподавание / Д. Пойа. – М.: Наука, 1976. – 448 с.
29. Репьев, В.В. Общая методика преподавания математики / В. В. Репьев. –М.: Учпедгиз, 1958. – 223 с.
30. Рубинштейн, С.Л. Основы общей психологии. Т.1. М.: Педагогика, 1989.
31. Рудин В.Н., Рудина Е.И. Графическое решение текстовых задач (пособие для учителей и школьников) / Издание Томского института повышения квалификации работников образования. 1995
32. Саранцев Г. И. Методика обучения математике в средней школе: учеб. пособие для студентов / Г. И. Саранцев. – М.: Просвещение, 2002. – 224 с.
33. Столяр А.А. Педагогика математики: Курс лекций / А. А. Столяр. – Минск: Выш. школа, 1974. – 382 с.
34. Селевко Г.К. Современные образовательные технологии. М.: 1998.
35. Современная методическая система математического образования: колл. монография / Н.С. Подходова [и др.]; под ред. Н.Л. Стефановой, Н.С. Подходовой, В.И. Снегуровой. – СПб: Изд-во РГПУ им. А.И. Герцена, 2009. – С. 24–27.
36. Шапиро И.М. Мотивационная функция задач в обучении математики / Сибирский межвузовский журнал «Педагог» http://www.altspu.ru/Journal/pedagog/pedagog_4/articl_12.html (дата обращения: 01.02.2018).
37. Эрдниев П.М., Теория и методика обучения математике в начальной школе. (педагогическая наука – реформе школы). – М.: Педагогика, 1988. -208с.