Методика применения геометрии масс в задачах школьного курса математики

У большинства обучающихся в результате решения огромного числа задач складывается представление, что существует необозримое число различных методов и способов решения математических задач и разобраться в этом многообразии очень сложно.

В первую очередь обучающиеся должны уяснить следующую общую идею, лежащую в основе всех методов и способов решения задач: чтобы решить какую-либо новую задачу, надо свести ее к одной или нескольким ранее решенным задачам.

Определимся с некоторыми понятиями:

• способ — совокупность действий для решения конкретной задачи;
• метод — общая схема (алгоритмическая или эвристическая), на основе которой строятся способы решения отдельных задач.

С этой точки зрения все математические задачи следует разделить на алгоритмические, или стандартные, и на эвристические, или нестандартные. Алгоритмические, или стандартные, задачи — это те, для решения которых в курсе математики имеется определенный алгоритм, и способ решения задач состоит в применении алгоритма к условиям решаемой задачи.

Для того чтобы ученик мог применить алгоритм к решению конкретной задачи, он должен:

• уметь вычленить этот алгоритм из определения, теоремы и увидеть его в правиле, формуле;
• уметь развертывать этот алгоритм в пошаговую программу.

Для решения же нестандартных задач обучающиеся должны сами изобрести (составить) способ их решения.

Чтобы поиск и изобретение способа решения таких задач производились обучающимися разумно, по определенному плану, они должны знать и владеть общими эвристическими методами решения математических задач. Эти общие методы следует сообщать обучающимся постепенно, иллюстрируя их достаточным числом примеров. К разбору этих методов необходимо возвращаться неоднократно при встрече с новыми задачами, где эти методы используются.

Рассмотрим основные методы.

Разбиение задачи на подзадачи

Суть метода: сложную задачу разбивают на несколько более простых, по возможности стандартных, задач, при последовательном решении которых можно решить данную задачу.

Этот метод имеет три разновидности:

• разбиение условия задачи на части: решение текстовых (сюжетных) задач «по вопросам»; используется и при решении очень многих других задач;
• разбиение требования задачи на части: часто требование задачи (вопрос) бывает таким сложным, что сразу ответить на него очень трудно, тогда, если возможно, целесообразно разбить его на несколько более простых вопросов.
• разбиение объекта задачи на части: объект задачи сложный или представляет собой бесконечное множество, то иногда полезно разбить его на части и решать задачу для каждой части отдельно.

Рассмотрим пример:

Задача.

Докажите, что не существует на плоскости таких четырех точек А, В, С и О, что треугольники АВС, ABD, ACD и BCD все остроугольные (предполагается, что никакие три из этих точек не лежат на одной прямой).

Объект этой задачи — четверки точек. На плоскости имеется бесконечное множество таких четверок точек. Разобьем их на части следующим образом. Первые три точки А, В и С могут образовать остроугольный треугольник АВС. Теперь остается доказать, что, где бы ни находилась точка D относительно ~ ABC, образующиеся при этом четыре треугольника не могут быть все остроугольные, т. е. по крайней мере один из них не остроугольный.

Четвертая точка D может находиться:

а) внутри АВС;

б) в одном из углов, вертикальных по отношению к внутренним углам АВС;

в) в одном из незамкнутых трехсторонников, образующихся стороной ~ АВС и продолжениями двух других сторон.

Таким образом, мы разбили исходную задачу на три более простые задачи, каждую из которых нетрудно решить.

Преобразование задачи

Суть метода: с помощью какого-либо приема мы преобразуем данную задачу в более простую, знакомую нам, эквивалентную задачу.

Данный метод очень широко применяется, так что трудно перечислить все те приемы, которые используются при этом. Наиболее известными являются прием замены неизвестных (метод подстановки), прием (метод) геометрических преобразований и т.д.

Кодирование объектов задачи

Суть метода: заменить данную задачу эквивалентной ей. Но в отличие от метода преобразования задачи, где замена происходила в пределах одного, и того же языка задачи (алгебраическая задача заменялась также алгебраической; геометрическая — геометрической) данный метод предполагает переход от одного языка к другому с помощью кодировки объектов задачи. Например, текстовая задача заменяется уравнением или системой уравнений, геометрическая задача с помощью введения системы координат заменяется алгебраической задачей и т.д.

Введение (построение) вспомогательных элементов

Данный метод используется для придания задаче определенности, если в ней имеются явно или неявно заданные неопределенные неизвестные, а также тогда, когда связь (отношение, зависимость) между данными и искомым непосредственно из условий задачи не видна (не может быть установлена). Классическим примером использования этого метода является решение задач «на бассейны».

Задача.

Через первую трубу бассейн заполняется водой за 10 ч, а через вторую — за 15 ч. За сколько часов наполнится бассейн, если открыть одновременно обе трубы?

При решении многих задач приходится использовать не один какой-то метод, а несколько.

Педагогу следует помнить, что учащиеся решают задачи не для того, чтобы найти их ответы, а для того, чтобы чему-то научиться, чем-то овладеть.

Решение задач есть вид творческой деятельности, а поиск решения есть процесс изобретательства. Чтобы этот поиск осуществлялся более эффективно, обучающимся следует предложить следующие рекомендации:

Рекомендации для поиска решения математических задач

• Прочитайте задачу. Попытайтесь установить, к какому виду задач она принадлежит.
• Если вы узнали в ней стандартную задачу знакомого вида, то примените для ее решения известное вам общее правило.
• Если же задача не является стандартной, то действуйте в следующих направлениях:
• вычлените из задачи или разбейте ее на подзадачи стандартного вида (способ разбиения);
• введите в условие вспомогательные элементы: вспомогательные параметры, вспомогательные построения (способ вспомогательных элементов);
• переформулируйте задачу, замените ее другой равносильной задачей (способ моделирования).
• Для того чтобы легче было осуществлять указанные способы, предварительно постройте наглядную вспомогательную модель задачи — ее схематическую запись.
• Решение нестандартных задач есть искусство, которым можно овладеть лишь в результате глубокого постоянного самоанализа действий по решению задач и постоянной тренировки в решении разнообразных задач.

Обучение решению математических задач

Фронтальное решение задач

Под фронтальным решением задач обычно понимают решение одной и той же задачи всеми обучающимися класса в одно и то же время. Организация фронтального решения задач может быть различной:

Устное фронтальное решение задач. Данный прием наиболее часто применяется учителями математики в среднем звене или начальной школе (IV-VII классах). Сюда можно отнести устные упражнения на вычисления; задачи-вопросы, истинность ответов которая подтверждается устными доказательствами. Данный прием должен стать обязательным элементом каждого урока, так как одной из задач обучения математике является обучение быстрым устным вычислениям. Данная задача должна решаться на всех этапах обучения - если ученики научатся устно выполнять вычисления и несложные преобразования, то не только на уроках математики, но и на уроках физики, химии освободится значительная часть времени, которое расходуется на нерациональное выполнение вычислений. В ходе организации устного фронтального решения задач учителю необходимо использовать различные средства обучения (таблички, таблицы, презентации, средства программированного обучения, ИКТ, SMART-технологии), что позволит значительно сэкономить время, отведенное на выполнение устных упражнений, повысит познавательную активность и плотность урока.

Письменное решение задач с записью на классной доске. В практике обучения немало таких ситуаций, в которых удобнее, чтобы одну и ту же задачу решали все ученики класса одновременно с решением этой же задачи на доске. При этом задачу на доске может решать либо учитель, либо ученик по указанию учителя.

Наиболее эффективным является письменное решение задач с записью на классной доске в следующих случаях:

• при решении первых после показа учителем задач по ознакомлению с новыми понятиями и методами;
• при решении задач, самостоятельно с которыми могут справиться не все ученики класса;
• при рассмотрении различных вариантов решения одной и той же задачи - для сравнения и выбора лучшего варианта;
• при разборе ошибок, допущенных несколькими учениками класса при самостоятельном решении задачи и т.д.

В ходе проектирования урока учитель должен предусмотреть и возможность одновременного решения задачи разными способами, вызвав сразу нескольких обучающихся к доске. Педагогу следует помнить, что решение одной задачи несколькими способами приносит больше пользы, чем решение подряд нескольких однотипных задач. Рассмотрение обучающимся различных вариантов решения, умение выбрать из них наиболее рациональных, свидетельствуют об умении ученика мыслить, рассуждать, проводить правильные умозаключения, воспитывает у учащихся гибкость мышления.

При этом следует учесть, что руководство решением задачи в этом случае требует от учителя определенного мастерства:

• правильно распределить свое внимание между обучающимися, решающими задачу у доски, и остальными учениками класса;
• организовать внимание обучающихся класса, решающих задачу, которое не должно рассеиваться действиями учеников у доски.

Письменное самостоятельное решение задач. Наиболее эффективной является такая организация решения математических задач, при которой ученики обучаются творчески думать, самостоятельно разбираться в различных вопросах теории и приложений математики. Самостоятельное решение обучающимися задач на уроках математики имеет многие преимущества:

• повышает учебную активность обучающихся, возбуждает их интерес к решению задач, стимулирует творческую инициативу, что способствует повышению эффективность урока;
• развивает мыслительную деятельность обучающихся;
• не имея возможности списывать решение задачи с доски, обучающийся вынужден сам осуществлять поиск решения задачи;
• выполняет контролирующую функцию и сокращает время, необходимое для опроса обучающихся, повышая плотность урока;
• учитель получает возможность индивидуализировать и дифференцировать процесс обучения, выявляя индивидуальные ошибки, подбирая задачи различного уровня сложности.

В ходе организации самостоятельного письменного решения задач учитель может предложить обучающимся самостоятельно изучить небольшой теоретический материал, разобрать образцы решения задач, предложенные учителем, а потом самостоятельно решать аналогичные задачи.

До начала проведения самостоятельной работы по решению математических задач необходимо провести инструктаж, в котором четко указать, что должны выполнить обучающиеся в работе, каков порядок ее выполнения, сроки выполнения и критерии оценивания. После проверки правильности самостоятельных решений проанализировать с обучающимися результаты работы.

Комментирование решения математических задач

Все обучающиеся работают на одной задачей, при этом один из них последовательно поясняет (комментирует) решение. Ученик должен не только рассказать последовательность выполнения действий, а объяснить, на каком основании (зачем) выполняется то или иное действие или преобразование. При этом каждый шаг в решении задачи должен быть оправдан ссылкой на известные математические предложения. Такое объяснение требует от обучающихся не только формального решения задачи, но и понимания сущности выполняемого преобразования, активной работы мысли. Обучающиеся, имеющие низкий уровень обученности математике или пробелы в знаниях, услышав объяснение каждого этапа решения задачи, могут попытаться выполнить решение самостоятельно. Но ведь этого и следует добиваться при решении задач.

Индивидуальное решение задач

Фронтальное решение учебных математических задач не всегда приводит к желаемым результатам в обучении математике. При фронтальной работе все обучающиеся решают одну и ту же задачу, и не осуществляется дифференцированный подход к обучению. А ведь для одних обучающихся эта задача может оказаться очень легкой, и они при решении такой задачи практически не почерпнут ничего нового, а для других ― вызвать серьезное затруднение. Поэтому необходим учет индивидуальных особенностей обучающихся и в связи с этим индивидуальный подбор задач. Задачи следует подбирать и систематизировать так, чтобы, с одной стороны, учитывались возможности и способности ученика, с другой стороны, его способности развивались.

Задача учителя — организовать решение математических задач с учетом уровня подготовки каждого ученика, что позволит овладеть необходимыми умениями и навыками слабым ученикам и в значительной степени совершенствоваться более сильным.

Поскольку в классе есть примерно равные по уровню учебных достижений обучающиеся, то можно подбирать задачи не для каждого ученика в отдельности (это было бы затруднительно для учителя), а для отдельных групп обучающихся. Подбор индивидуальных заданий преследует цель для каждой выбранной учителем группы обучающихся составить систему задач. Эти группы не должны иметь постоянного состава: обучающиеся по мере овладения необходимыми знаниями должны иметь возможность перехода из одной группы в другую.

Индивидуальные формы работы более эффективны (по сравнению с фронтальными) и в ходе работы по устранению пробелов знаний. Пробелы можно выявить выполнением проверочных и контрольных и индивидуальных работ. При этом сильным обучающимся достаточно сказать о неверности результата, некоторым ученикам следует подчеркнуть ошибки, а слабо подготовленным - исправить. В ходе осуществления коррекционной работы задачи необходимо подбирать, учитывая причины, вызвавшие ошибку.

Индивидуальное решение задач продолжается и в ходе выполнения домашней работы. Содержание задач и упражнений, предлагаемых для домашней работы обучающихся, должно быть подготовлено предшествующей работой на уроке. Это не означает, что для домашнего решения должны предлагаться лишь задачи, аналогичные решенным в классе. Ведь домашнее задание имеет целью не только закрепление изученного на уроке, но и дальнейшее совершенствование математических знаний, умений и навыков.

Поскольку обучающиеся обычно имеют индивидуальные особенности, различную подготовку, следует индивидуализировать домашние задания. Так домашнее задание может быть направлено на устранение пробелов, закрепление и совершенствование знаний, приобретенных на уроке, углубление изученного. Следует отметить, что ученики с большим желанием решают задачи, предложенные им в индивидуальном порядке.

К числу наиболее сложных геометрических задач школьного курса математики относятся задачи, которые связаны с делением отрезков в контексте треугольника в заданном отношении. Как правило, их решению предшествуют дополнительные построения, что значительно усложняет поиск решения. В этом случае иногда целесообразно привлечь на помощь физику. При рассмотрении геометрических фигур, как моделей реально существующих физических тел, в силу вступает геометрия масс.

При решении задач методом, предлагаемым к рассмотрению, нам понадобятся два геометрических факта:

1. Отношение площадей треугольников с общей высотой равно отношению их оснований:
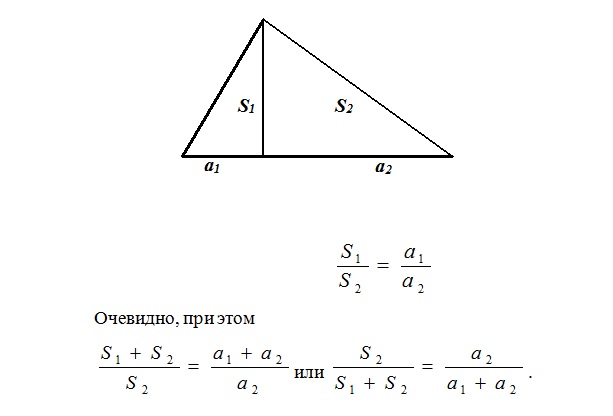
2. Отношение площадей треугольников с общим (или одинаковым) углом равно отношению произведений сторон, заключающих этот угол:

отношению их оснований:

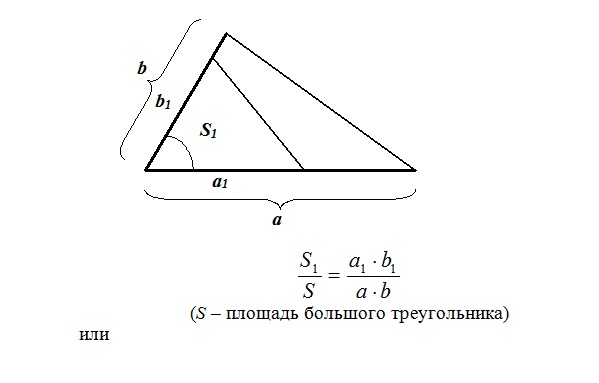
Познакомимся с основными моментами теоретического материала по теме «Геометрия масс».

Понятие центра масс применяется к системе материальных точек на плоскости. Поэтому сначала определимся с тем, что такое материальная точка. Рассмотрим обычную точку А на плоскости. Сопоставим ей так называемую массу m – некоторое действительное число, не равное нулю. Точка вместе с приписанной ей массой получила название материальной точки.

Тогда центр масс Z двух точек А и В с массами m и n находится на прямой так, что отношение

Проиллюстрируем утверждение. Представим штатив, на котором закреплена невесомая планка с прикрепленными на концах грузиками и при этом конструкция находится в равновесии.

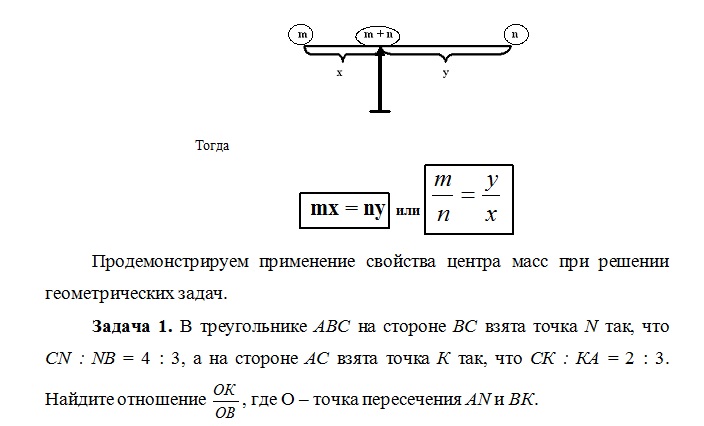
Традиционно при решении этой задачи на уровне школьной программы используется метод площадей, что требует дополнительных построений.

Решим сначала эту задачу традиционным методом. В этом случае необходимо провести отрезок ОС.

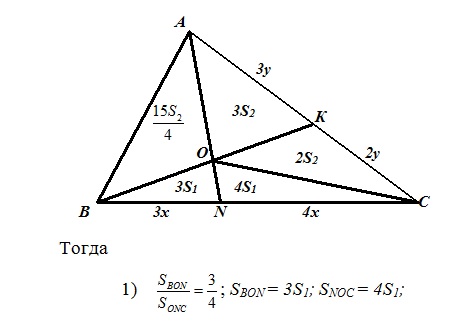
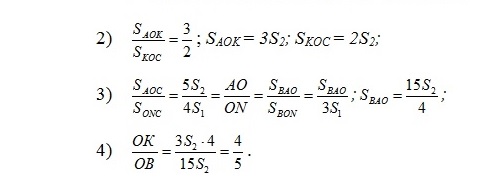
Решим эту же задачу с применением метода геометрии масс.

Будем рассматривать стороны треугольника как планки, на концы которых необходимо крепить грузики так, чтобы в каждом случае система оказывалась в равновесии.

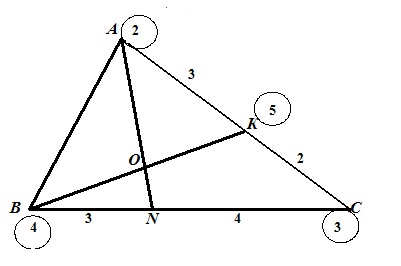
Коэффициент пропорциональности в этом случае не используется. Не важно, в каких единицах выражены части сторон треугольника, значимость имеют лишь количественные характеристики.

Тогда выбираем любую из сторон треугольника, разделенную точкой на части, и «крепим» на ее концах грузики так, чтобы в точке на стороне достигалось равновесие. Например, для стороны ВС в точке В «крепим» грузик массой 4, тогда в точке С – грузик массой 3 (4 · 3 = 3 · 4). Для обеспечения наглядности массы обводим окружностями. Далее рассматриваем сторону АС и добиваемся равновесия в точке К: 3 · 2 = х · 3, откуда х = 2. Тогда в точке К мы получаем массу 3 + 2 = 5.

В итоге (напоминаем, что массы обратно пропорциональны длинам отрезков).

Если учесть, что решение задачи предложенным способом представляет собой рассуждения, которые в случае освоения метода выполняются устно, и вычисления при этом минимальны, то становится очевидным преимущество геометрии масс перед методом площадей.

Рассмотрим различные ситуации, в которых целесообразно применять предлагаемый метод.

Задача 2. В треугольнике RPQ на стороне RQ взята точка N так, что RN : NQ = 2 : 7, а на стороне RP взята точка F так, что RF : FP = 3 : 1. Найдите длину отрезка МN, где М – точка пересечения отрезков QF и PN, если РМ = 12.

Решение:

В этом случае речь идет уже не об отношении длин отрезков, а о нахождении конкретного значения длины отрезка. При этом ход рассуждений сохраняется.

Рассмотрим точки R и Q как материальные. Так как RN : NQ = 2 : 7, то длина RN равна 2, а длина NQ равна 7. Тогда для достижения равновесия в точке N «крепим» к точке R грузик массой 7, а к точке Q – грузик массой 2.

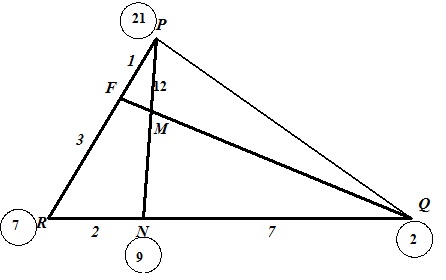
Рассмотрим теперь материальные точки R и Р. Исходя из условия, длина RF равна 3, а длина FP равна 1. Тогда, учитывая, что точке R уже поставлена в соответствие масса 7, необходимо для достижения равновесия в точке F «прикрепить» в точку Р грузик массой .

Тогда

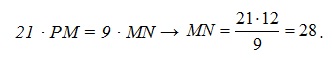
Ответ: 28.

Чаще всего в задачах рассматриваемого типа речь идет о нахождении площади. Рассмотрим такие задачи.

Задача 3. В треугольнике АВС прямые АМ (М ВС) и СN (N АВ) пересекаются в точке О и делят стороны АВ и ВС в отношении АN : N B = 2 : 3, CM : MB = 2 : 1. Найти площадь четырехугольника NBMO, если площадь треугольника АВС равна 15.

Решение:

Выполним построение и «прикрепим» к вершинам треугольника грузики так, чтобы в точках на сторонах достигалось равновесие:

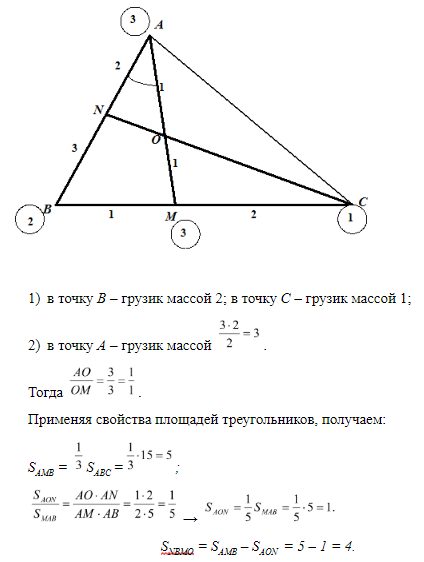
Ответ: 4

Задача 4. В треугольнике АВС на стороне ВС взята точка К так, что прямая АК делит пополам биссектрису ВМ. Найти площадь треугольника, если АВ : ВС = 1 : 3 и SВОК = 3, где О – точка пересечения АК и ВМ.

Решение:

Прежде всего, воспользуемся свойством биссектрисы треугольника:

АВ : ВС = АМ : МС = 1 : 3.

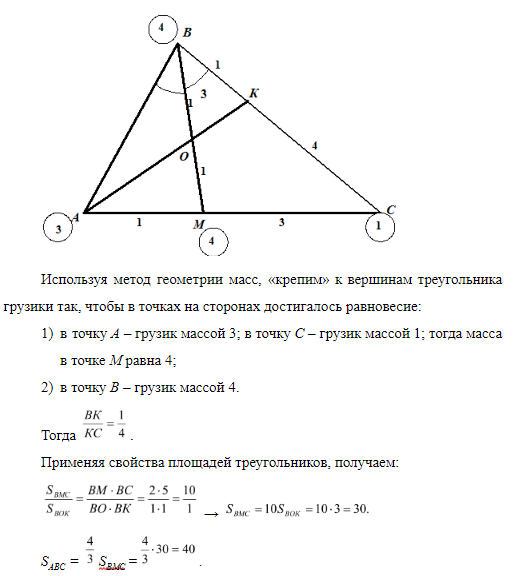
Ответ: 40.

Задача 5. В равнобедренном треугольнике АВС через вершины основания С и В и точку N (N лежит на высоте, проведенной к основанию, и делит ее в отношении 1 : 3, считая от основания) проведены прямые CD и ВЕ (D АВ; Е АС). Найдите площадь треугольника BDE, если площадь треугольника АВС равна 20.

Решение:

Прежде всего, воспользуемся свойством биссектрисы треугольника:

АВ : ВС = АМ : МС = 1 : 3.

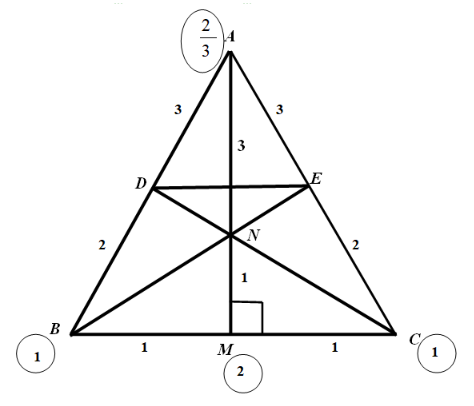
Используя метод геометрии масс, «крепим» к вершинам треугольника грузики так, чтобы в точках на стороне и высоте достигалось равновесие:

1. в точку В и точку С – грузики массой 1; тогда масса в точке М равна 2;

Все предыдущие задачи решались после применения метода геометрии масс арифметически (по действиям). Рассмотрим задачи, требующие алгебраического подхода (введения переменных).

Задача 6. В треугольнике АВС прямая АМ (М ВС) пересекает ВС и делит ее в отношении СМ : МВ = 3 : 2. Прямая СN (N АВ) пересекает АМ в точке О и делит ее в отношении АО : ОМ = 5 : 1. Найти площадь треугольника АВС, если площадь четырехугольника NBMO равна 6.

Решение:

Используя метод геометрии масс, «крепим» к вершинам треугольника грузики так, чтобы в точках на сторонах достигалось равновесие:

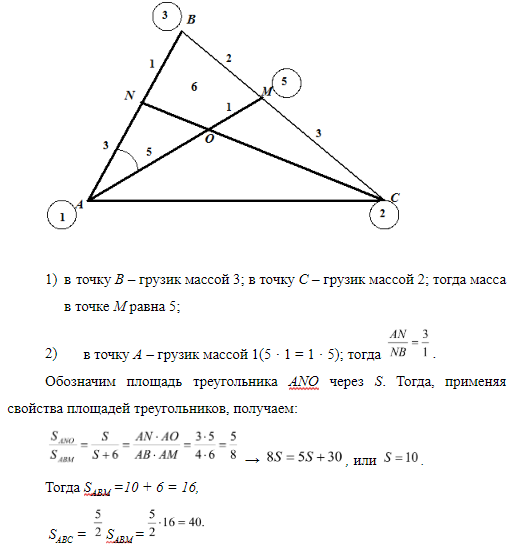
Ответ: 40.

Задача 7. Точка К лежит на стороне АВ, а точка М – на стороне АС треугольника АВС, причем АК : КВ = 3 : 2, АМ : МС = 4 : 5. Прямая, проходящая через точку К параллельно ВС, пересекает отрезок ВМ в точке Р. Найти отношение ВР : РМ.

Решение:

Используя метод геометрии масс, «крепим» к вершинам треугольника грузики так, чтобы в точках на сторонах достигалось равновесие:

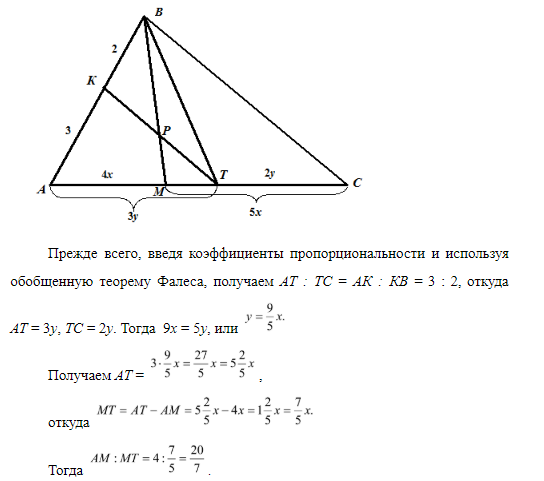
С учетом полученных выводов, выполняем новый чертеж.

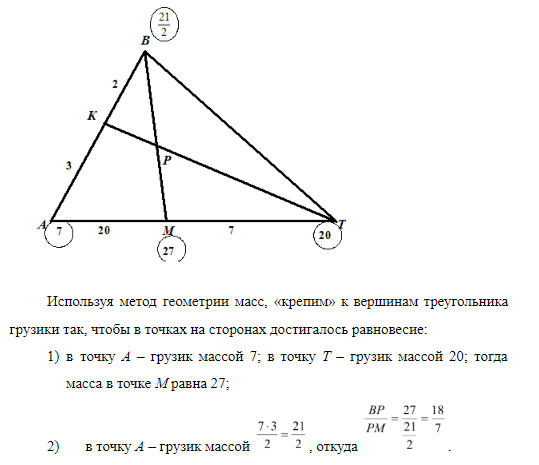
Ответ: 18/7.

Иногда первоначальная фигура не является треугольником, для которого применим метод геометрии масс, но дополнительные построения позволяют получить необходимую конструкцию.

Задача 8. На сторонах АВ и АD прямоугольника АВСD взяты точки Е и К соответственно так, что АЕ = ВЕ и АК : DК = 3 : 2. Отрезки DЕ и ВК пересекаются в точке О. Площадь треугольника ВОЕ равна 15. Найдите площадь треугольника DОК.

Решение:

Для применения метода геометрии масс достаточно в данном прямоугольнике провести диагональ ВD.

«Крепим» к вершинам треугольника АВD грузики так, чтобы в точках на сторонах достигалось равновесие:

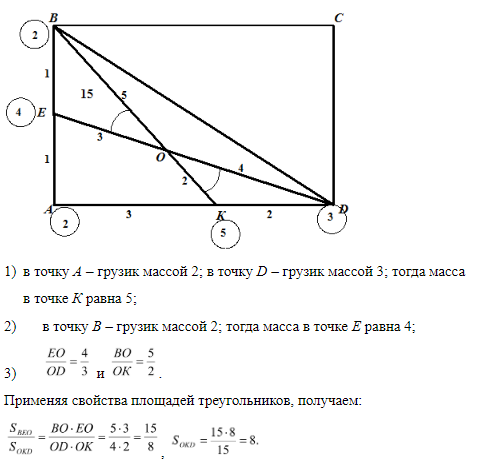
Ответ: 8.

Задача 9. В треугольнике АВС на сторонах АВ и АС отмечены соответственно точки К и L так, что АК : КВ = 1 : 2, AL : LC = 2 : 1. Если отрезок КL пересекает медиану АD в точке О, то каким будет отношение АО : ОD? (4 : 5)

Решение:

Особенность этой задачи заключается в том, что не все точки, делящие стороны треугольника на части, соединены с вершинами треугольника. Точки К и L соединены друг с другом. В этом случае будем называть сторону, точка на которой соединена с вершиной, «хорошей» стороной. Тогда будем начинать «крепить» грузики всегда с «хорошей» стороны.

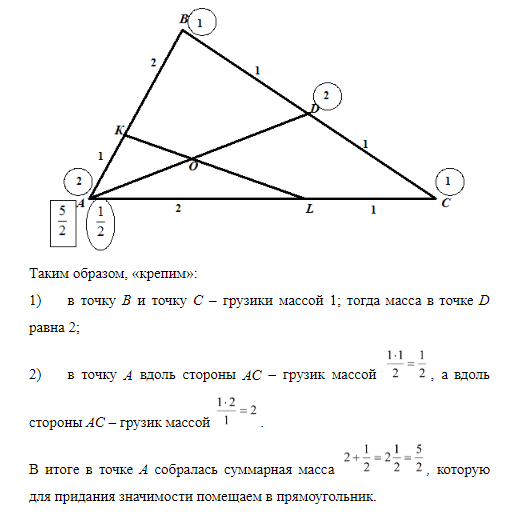
Тогда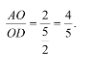

Ответ: 4/5.

Рассмотрим еще пару задач, которые обладают аналогичной особенностью.

Задача 10. В треугольнике АВС на сторонах АВ, ВС и АС отмечены соответственно точки К, L и D так, что АК : КВ = 1 : 4, ВL : LC = 1 : 2, AD = DC. Найдите площадь треугольника АВС, если площадь треугольника ВОL равна 20, где О – точка пересечения КL и BD.

Решение:

Начинаем «крепить» грузики с «хорошей» стороны, то есть стороны АС (точка D на ней соединена с вершиной треугольника).

Тогда «крепим»:

1. в точку А и точку С – грузики массой 1; тогда масса в точке D равна 2;

Применяя далее свойства площадей треугольников, получаем:

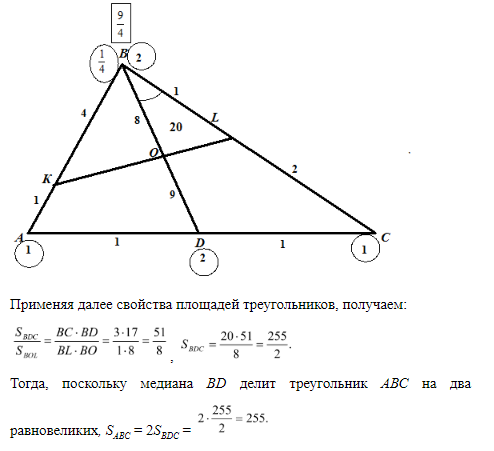
Ответ: 255.

Задача 11. На сторонах МN и NР прямоугольника МNРQ взяты точки А и В соответственно так, что АМ : NА = 2 : 3, ВN : ВР = 1: 3. Отрезки ВМ и АQ пересекаются в точке О. Площадь четырехугольника АNВО равна 47. Найдите площадь прямоугольника МNРQ.

Решение:

В решенной ранее задаче в контексте прямоугольника достаточно было провести диагональ для того, чтобы метод геометрии масс был применим. В данном случае проведение любой из диагоналей ведет к «рассечению» значимых элементов задачи на части. Целесообразно при этом провести все же диагональ МР, поскольку она оставляет нетронутым четырехугольник АNВО, площадь которого известна по условию.

Пусть проведенная диагональ МР и отрезок АQ пересекаются в точке Т. Тогда можно заметить, что ∆АТМ ~ ∆QTP, откуда .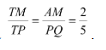

С этого момента можно рассматривать задачу в контексте треугольника МNР.

«Крепим» к вершинам треугольника МNР грузики так, чтобы в точках на сторонах достигалось равновесие. При этом начинаем с «хорошей» стороны, то есть со стороны NP (точка В на ней соединена с вершиной треугольника).

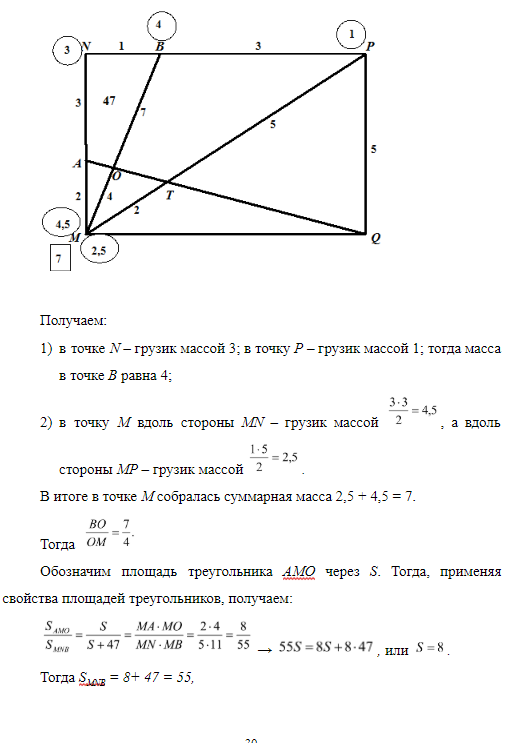
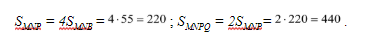
Ответ: 440.

Следует отметить, что обратиться к методу геометрии масс можно и при решении некоторых стереометрических задач. Приведем примеры.

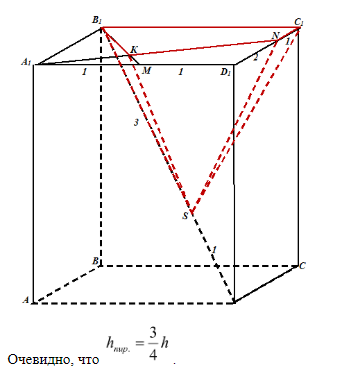
Задача 12. АВСDА1В1С1D1 – прямоугольный параллелепипед, площадь основания которого равна 48. Точка N лежит на ребре АD так, что АN : ND = 2 : 1. Точка М – середина ребра АВ. Отрезки ВN и СМ пересекаются в точке К. Найдите объем пирамиды В1КСDN, если СС1 = 12.

Решение:

Выполним сначала чертеж параллелепипеда и выясним, что необходимо узнать для того, чтобы найти объем указанной в условии пирамиды. Для обеспечения наглядности пирамиду выделим красным цветом. Как известно, объем пирамиды находится по формуле . Очевидно, что высота пирамиды совпадет с ребром ВВ1 параллелепипеда, а, значит, равна по условию 12.

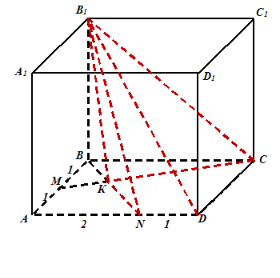
Задача сводится к нахождению площади основания пирамиды. Возникает необходимость рассмотреть выносной чертеж прямоугольника, являющегося основанием параллелепипеда.

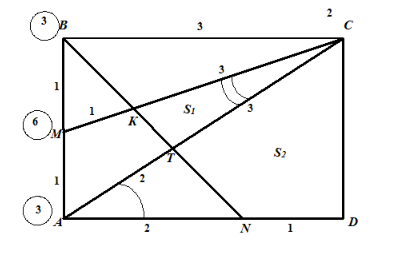
Очевидно, что необходимо провести диагональ АС, которая делит прямоугольник на две равновеликие части, площадь каждой из которых равна 24. Тогда основание пирамиды КСDN разделилось на две части: треугольник КСТ и четырехугольник ТСDN, площади которых для удобства обозначим соответственно, как S1 и S2.

Далее применим метод геометрии масс в контексте треугольника АВС для нахождения площади S1. «Крепим» к вершинам треугольника грузики так, чтобы в точках на сторонах достигалось равновесие:

1. в точку А – грузик массой 3; в точку С – грузик массой 2;
2. в точку В – грузик массой 3, тогда масса в точке М равна 6, откуда .

Тогда, применяя свойство площадей треугольников, получаем:

Ответ: 92.

Задача 13. АВСDА1В1С1D1 – прямая четырехугольная призма, объем которой равен 960. Основанием призмы является параллелограмм АВСD. Точки М и N принадлежат ребрам А1D1 и С1D1 так, что А1М : А1D1 = 1 : 2, D1N : NС1 = 2 : 1. Отрезки А1N и В1М пересекаются в точке К. Найдите объем пирамиды SВ1KNС1, если S В1D и В1S : SD = 3 : 1.(115)

Решение:

В данном случае рассматривается прямой параллелепипед, в основании которого параллелограмм. Объем параллелепипеда может быть найден по формуле Поскольку объем пирамиды находится по формуле 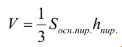, необходимо выразить высоту пирамиды через высоту параллелепипеда (обозначим через h), а основание пирамиды через площадь параллелограмма, являющегося основанием параллелепипеда (обозначим через S).

Задача сводится к выражению площади основания пирамиды через S. Возникает необходимость рассмотреть выносной чертеж параллелограмма, являющегося основанием параллелепипеда.

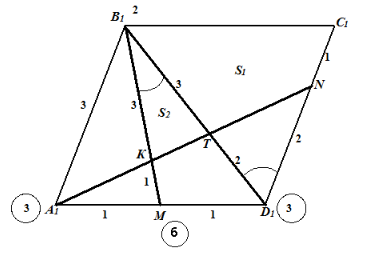
Проведем диагональ В1D1, которая разделит параллелограмм на две равновеликие части, площадь каждой из которых равна S/2. Тогда основание пирамиды КВ 1С1N разделилось на две части: четырехугольник ТВ1С1N и треугольник КВ1Т, площади которых для удобства обозначим соответственно, как S 1 и S 2.

Далее применим метод геометрии масс в контексте треугольника А1В1D1 для нахождения площади S2. «Крепим» к вершинам треугольника грузики так, чтобы в точках на сторонах достигалось равновесие:

1. в точку B1 – грузик массой 2; в точку D1 – грузик массой 3;
2. в точку A1 – грузик массой 3, тогда масса в точке М равна 6, откуда .

Ответ: 115.

Таким образом, метод геометрии масс следует пытаться применять в ситуациях, когда в задаче речь идет об отношении длин отрезков, которые могут быть рассмотрены в контексте треугольника.

Список литературы:

1. Азаров А.И. Математика за курс базовой школы: обучение: экзамен: тестирование. – Минск: Аверсэв, 2006. – 480 с.: ил. – (Школьникам, абитуриентам, учащимся).
2. Асмолов А. Г. и др. «Формирование УУД в основной школе: от действия к мысли». Система заданий. М. «Просвещение», 2010
3. Асмолов А.Г. Как проектировать универсальные учебные действия в школе: от действия к мысли: пособие для учителя. М.: Просвещение, 2008.
4. Астряб А.М. Наглядная геометрия. / А.М. Астряб – М.: Книга по Требованию, 2013. – 160 с.
5. Бруцкая О.А. Программа по математике в соответствии с требованиями ФГОС/ Первое сентября. 2014. № 6. [Электронный ресурс] – Режим доступа. – URL: http://festival.1september.ru/articles/627066/ (в открытом доступе).
6. Булынин В. Математика, № 14, 2005 с. 39 – 41, Применение графических методов при решении текстовых задач.
7. Балк М.Б.. Геометрические приложения понятия о центре тяжести. – Москва: Государственное издательство физико-математической литературы, 1959.
8. Блинова Т.Л. Современные аспекты методики обучения математике / Т. Л. Блинова, Э. А. Власова, И. Н. Семенова, А. В. Слепухин. – Екатеринбург, 2007. – 190 с.
9. Бабанский Ю. К. Оптимизация процесса обучения / Ю. К. Бабанский. –М., 1982. – 192 с.
10. Вавренчук Н.А. Формирование математической речи младших школьников. Сб. материалов Междунар. Науч.- практ. Конф., Брест, 15-17 мая 2007г
11. Вахрушев А.А., Горячев А.В., Данилов Д.Д., Бунеева Е.В., Чиндилова О.В., Козлова С.А. Программа личностного развития и формирования универсальных учебных действий у обучающихся на ступени начального образования (образовательная система «Школа 2100»). // Народное образование. – 2010. -№1.
12. Веременюк В.В.: Тренажер по математике для подготовки к централизованному тестированию и экзамену. – Минск: ТетраСистемс, 2007. – 176 с.
13. Груденов Я.И. Совершенствование методики работы учителя математики: Кн. для учителя / Я. И. Груденов. – М.: Просвещение, 1990. – 224 с.
14. Действующие учебники по математике для учащихся общеобразовательных учреждений.
15. Егерев В.К., Зайцев В.В., Кордемский Б.А. и другие. Сборник задач по математике для поступающих в вуз, учебное пособие. / под редакцией М. И. Сканави – Мн: Выш. шк., 1990 – 528 с.: ил.
16. Куимова Е. И., Куимова К. А., Титова Е. И. Функции задач в обучении математике // Молодой ученый. — 2014. — №12. — С. 280-281. — URL https://moluch.ru/archive/71/12175/ (дата обращения: 01.02.2018).
17. Крутецкий В.А. Психология математических способностей школьников/ Под редакцией Н.И. Чуприковой. М.: Издательство «Институт практической психологии»; Воронеж: Издательство НПО «МОДЭК», 1998. – 416 с.
18. Лабораторные и практические работы по методике преподавания математики: Учеб. пособие для студентов / Е. И. Лященко, К. В. Зобкова Т. Ф. Кириченко и др.; Под ред. Е.И. Лященко. – М.: Просвещение, 1988. –223 с.
19. Ложкина Е.М., Походова И.С. Введение в моделирование. Математические модели в естествознании (биология, химия, экология). – СПб: Изд-во РГПУ им. А.И. Герцена, 2009.
20. Литвиненко В.Н., Мордкович А.Г. Практикум по элементарной математике: Алгебра. Тригонометрия. 2-ое издание, переработанное и дополненное. М.: Просвещение, 1991 – 352 с.
21. Манвелов С. Г. Конструирование современного урока математики: кн. для учителя / С. Г. Манвелов. – М.: Просвещение, 2002. – 175 с.
22. Методика и технология обучения математике. Курс лекций: пособие для вузов / Н. Л. Стефанова, Н. С. Подходова и др. – М.: Дрофа, 2005. – 416 с.
23. Методика преподавания математики в средней школе. Общая методика: учеб. пособие для студ. физ.-мат. ф-тов пед. ин-тов / В. А. Оганесян. М. Колягин. – М.: Просвещение, 1980. – 368 с.
24. Методика преподавания математики в средней школе. Общая методика: учеб. пособие для студ. пед. ин-тов спец. 2104 Математика и 2105 Физика / А. Я. Блох, Е. С. Канин и др. – М.: Просвещение, 1985. – 336
25. Методика обучения математике: вопросы теории и практики. Учебное пособие для студентов. /Петрова А.И, Жирков Е.П, Аргунова Н.В, Макарова С.М, Ефремов В.П. Якутск: Издательско-полиграфический комплекс СВФУ, 2011. – 138 с.
26. Методика обучения математике в 2 ч. Часть 1: учебник для академического бакалавриата / Н. С. Подходова [и др.]; под ред. Н. С. Подходовой, В. И. Снегуровой. — М.: Издательство Юрайт, 2017. — 274 с.
27. Орлов. В.В. Геометрия в задачах: 7 – 9 класс. – СПб: Мир и семья – 95; Интерлайн, 1999.
28. Пойа Д. Математическое открытие. Решение задач: основные понятия, изучение и преподавание / Д. Пойа. – М.: Наука, 1976. – 448 с.
29. Репьев, В.В. Общая методика преподавания математики / В. В. Репьев. –М.: Учпедгиз, 1958. – 223 с.
30. Рубинштейн, С.Л. Основы общей психологии. Т.1. М.: Педагогика, 1989.
31. Рудин В.Н., Рудина Е.И. Графическое решение текстовых задач (пособие для учителей и школьников) / Издание Томского института повышения квалификации работников образования. 1995
32. Саранцев Г. И. Методика обучения математике в средней школе: учеб. пособие для студентов / Г. И. Саранцев. – М.: Просвещение, 2002. – 224 с.
33. Столяр А.А. Педагогика математики: Курс лекций / А. А. Столяр. – Минск: Выш. школа, 1974. – 382 с.
34. Селевко Г.К. Современные образовательные технологии. М.: 1998.
35. Современная методическая система математического образования: колл. монография / Н.С. Подходова [и др.]; под ред. Н.Л. Стефановой, Н.С. Подходовой, В.И. Снегуровой. – СПб: Изд-во РГПУ им. А.И. Герцена, 2009. – С. 24–27.
36. Шапиро И.М. Мотивационная функция задач в обучении математики / Сибирский межвузовский журнал «Педагог» http://www.altspu.ru/Journal/pedagog/pedagog_4/articl_12.html (дата обращения: 01.02.2018).
37. Эрдниев П.М., Теория и методика обучения математике в начальной школе. (педагогическая наука – реформе школы). – М.: Педагогика, 1988. -208с.