Формулы приведения

Определение

Если под знаком тригонометрической функции содержится выражение \(\frac{\pi}{2}+t,\frac{\pi}{2},\pi+t,\pi-t,\frac{3\pi}{2}+t,\frac{3\pi}{2}-t\) и вообще любое выражение вида \(\frac{\pi n}{2}\pm t\) ,где \(n\) – произвольное целое число, то такое выражение всегда можно привести к более простому виду, при котором под знаком тригонометрической функции будет содержаться только аргумент \(t\).
Соответствующие формулы обычно называют формулами приведения.

Пример

Укажем некоторые формулы приведения.

\(\sin(\pi+t)=-\sin t \\ \cos(\pi+t)=-\cos t \\ \sin(\frac{\pi}{2}+t)=\cos t \\ \cos(\frac{\pi}{2}+t)=-\sin t \\ tg(\pi+t)=tg\;t \\ ctg(\pi+t)=ctg\;t\)

Для простого и удобного способа запоминания формул приведения было придумано мнемоническое правило, суть которого в следующем:

Если под знаком преобразуемой тригонометрической функции содержится выражение \(\pi \pm t\) или \(2\pi \pm t\) , то наименование тригонометрической функции следует сохранить.
Если под знаком преобразуемой тригонометрической функции содержится выражение \(\frac{\pi}{2}\pm t\) или \(\frac{3\pi}{2}\pm t\), то наименование тригонометрической функции следует изменить на родственное (синус – на косинус, косинус – на синус, тангенс – на котангенс, котангенс – на тангенс).
Иногда для обозначения родственной тригонометрической функции используют понятие кофункция. Например, косинус – это кофункция для синуса и наоборот. Тангенс – это кофункция для котангенса и наоборот.
Перед полученной функцией от аргумента \(t\) надо поставить тот знак, который имела бы преобразуемая (старая) функция при условии, что угол \(t\) принадлежит первой четверти, т.е. \(0 < t < \frac{\pi}{2}\).
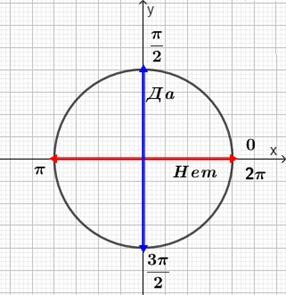
Данное правило можнографически пояснить простым алгоритмом из двух вопросов:

Меняем функцию на кофункцию? При переводе головы по красной стрелке на рисунке, мы образно отвечаем «нет».
Красной стрелке на рисунке соответствуют те значения аргумента, при которых функция не меняется на кофункцию: \(0,\pm\pi,\pm2\pi,\pm3\pi,...,n\pi\)
При переводе головы по синей стрелке на рисунке, мы образно отвечаем «да».
Синей стрелке на рисунке соответствуют те значения аргумента, при которых функция меняется на кофункцию: \(\pm+\frac{\pi}{2},\pm\frac{3\pi}{2},\pm\frac{5\pi}{2},...,\frac{(2n-1)\pi}{2}\)

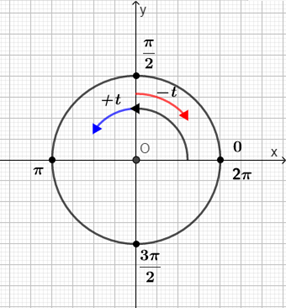
Знак выражения? Определяем четверть, куда попадает аргумент тригонометрической функции.
Помним, что угол \(t\) находится в пределах одной четверти, т.е. меньше \(90^{\circ}\).
Все выражения вида \(\frac{n\pi}{2} + t\) подразумевают увеличение опорного угла \(\frac{n\pi}{2}\) на угол \(t\), т.е. добавочный поворот на \(t\) в (положительном) направлении против часовой стрелки.
Все выражения вида \(\frac{n\pi}{2} – t \) подразумевают уменьшение опорного угла \(\frac{n\pi}{2}\) на угол \(t\), т.е. поворот в обратном (отрицательном) направлении на t по часовой стрелке.