Комплексные числа и координатная плоскость
Геометрической моделью множества комплексных чисел является координатная плоскость.
Алгебраический способ изображения комплексного числа:
Каждому комплексному числу \(z = a+bi\) можно поставить в соответствие точку \((a;b)\) координатной плоскости.
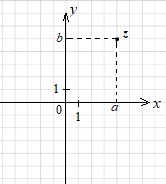
Изобразим на координатной плоскости числа \(z_1 = 2+3i, z_2 = 5−4i\).
построим точку \(z_1\) с координатами \((2;3)\)
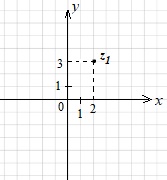
построим точку \(z_2\) с координатами \((5;-4)\)
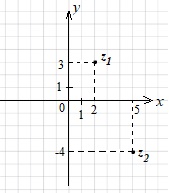
Векторный способ изображения комплексного числа:
Каждому комплексному числу \(z = a+bi\) можно поставить в соответствие вектор с началом в точке \((0;0)\) и концом в точке \((a;b)\).
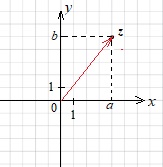
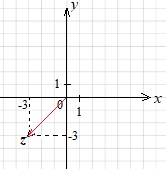
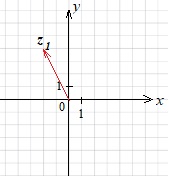
Изобразим на координатной плоскости вектор, соответствующий числу \(z = −3−3i\).
Построим вектор с началом в точке \((0;0)\) и концом в точке \((-3;-3)\)
Геометрическое изображение суммы комплексных чисел:
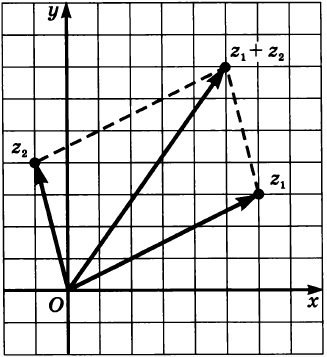
Изобразим на координатной плоскости сумму чисел \(z_1 = 4−2i\) и \(z_2 = 2+3i\).
построим вектор \(z_1\) с началом в точке \((0;0)\) и концом в точке \((4;-2)\)
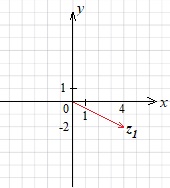
построим вектор \(z_2\) с началом в точке \((0;0)\) и концом в точке \((2;3)\)
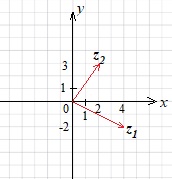
достроим параллелограмм на векторах \(z_1\) и \(z_2\)
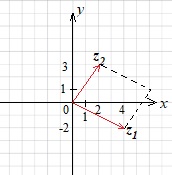
построим вектор \(z_1+z_2\) с началом в точке \((0;0)\), являющийся диагональю параллелограмма.
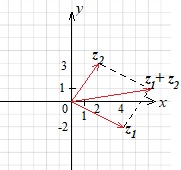
Геометрическое изображение разности комплексных чисел:
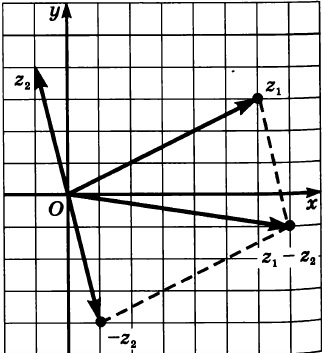
Изобразим на координатной плоскости разность чисел \(z_1 = −2+4i\) и \(z_2 = 4+i\).
построим вектор \(z_1\) с началом в точке \((0;0)\) и концом в точке \((-2;4)\)
построим вектор \(z_2\) с началом в точке \((0;0)\) и концом в точке \((4;1)\)
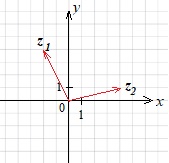
построим вектор \(-z_2\) с началом в точке \((0;0)\) и концом в точке \((-4;-1)\)
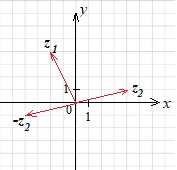
достроим параллелограмм на векторах \(z_1\) и \(–z_2\)
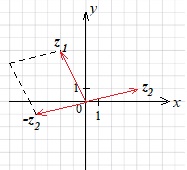
построим вектор \(z_1−z_2\) с началом в точке \((0;0)\), являющийся диагональю параллелограмма.
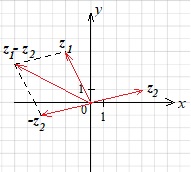
Геометрическое изображение комплексного числа, умноженного на действительное число:
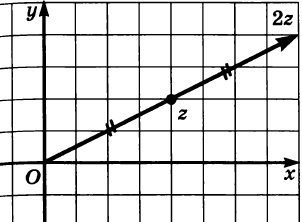
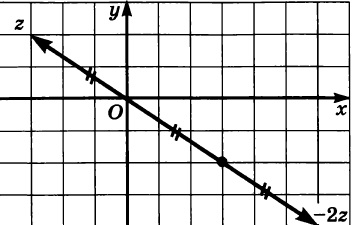
Изобразим на координатной плоскости число \(2z\), если \(z = −3+2i\).
построим вектор \(z\) с началом в точке \((0;0)\) и концом в точке \((-3;2)\)
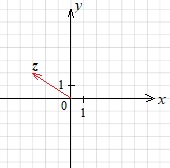
на луче \(OZ\) отложим вектор, длина которого в два раза больше вектора \(z\).
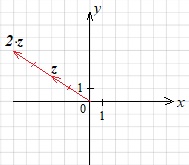
Геометрическое изображение сопряжённых комплексных чисел:
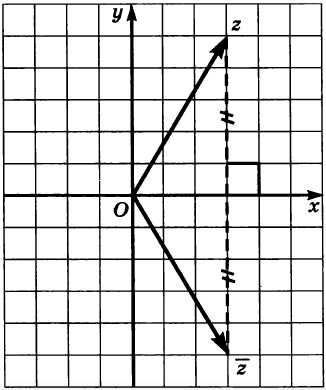
Изобразим на координатной плоскости число \(\overline{z}\), если \(z = 4+3i\).
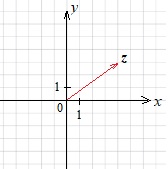
построим вектор \(z\) с началом в точке \((0;0)\) и концом в точке \((4;3)\)
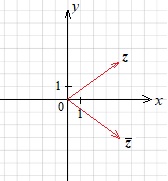
построим вектор \(\overline{z}\) с началом в точке \((0;0)\) и концом в точке \((4;-3)\).
© ООО «Знанио»
С вами с 2009 года.
![]()
