Натуральный логарифм. Функция y=ln x её свойства, график, дифференцирование

Определение

Если основанием логарифма служит число \(e\) (число Эйлера), то говорят, что задан натуральный логарифм.
Для натуральных логарифмов, как и для десятичных, принято специальное обозначение: \(\ln\) (\(l\) – логарифм, \(n\) – натуральный).
Например, вместо \(\log_e2\) пишут \(\ln{2}\).

График логарифмической функции \(y = \log_ax\) симметричен графику показательной функции \(y=a^x\) относительно прямой \(y=x\).
Значит, и график функции \(y=\ln{x}\) симметричен графику функции \(y=e^x\) относительно прямой \(y=x\).

Свойства функции \(y=\ln{x}\):

Область определения функции – только положительные числа: \(D(y)=(0; +\infty)\)
Множество значений функции – все действительные числа \(\mathbb{R}\) : \(E(y)=(-\infty;+\infty)\)
не имеет ни наибольшего, ни наименьшего значений
не является ни четной, ни нечетной
возрастает на всей области определения (на \(D(f)\))
непрерывна
не ограничена ни сверху, ни снизу
имеет производную для любого значения \(x > 0\), причем справедлива формула: \[(\ln{x})'=\frac{1}{x}.\]

Пример

Построим уравнение касательной к графику функции \(y=\ln{x}\) в точке \(x=e\).

Напомним, что уравнение касательной к графику функции \(y=f(x)\) в точке \(x=a\) имеет вид:
\(y=f(a)+f'(a)(x-a)\)

Воспользуемся алгоритмом составления уравнения касательной к графику функции, учитывая, что в нашем примере \(f(x)=e^x\).

точка \(a=e\)
вычисляем \(f(a)=f(e)=\ln{e}=1\)
вычисляем производную в точке \(a=e\): \(f'(x)=\frac{1}{x} \;\; \Rightarrow \;\; f'(a)=f'(e)=\frac{1}{e}\)
подставляем найденные значения \(a=e, f(a)=1,f'(a)=\frac{1}{e}\) в формулу касательной.
Получим: \(y=1+\frac{1}{e} \cdot (x-e)\)
После упрощения имеем: \(y=\frac{x}{e}\)

Изображаем график функции \(y=\ln{x}\) и касательную к нему в точке \(x=e\).

Ответ: \(y=\frac{x}{e}\).

Пример

Вычислим значение производной функции \(y=\ln{(3x+5)}\) в точке \(x=-1\)

Воспользуемся правилом дифференцирования функции \(y=f(kx+m)\), согласно которому \(y'=k \cdot f'(kx+m)\), и тем, что \((\ln{x})'=\frac{1}{x}\)

В нашем примере \(f(kx+m)=\ln{(3x+5)}\).
Применяя правило, получим: \(y'=(\ln(3x+5))'=3 \cdot \frac{1}{3x+5}=\frac{3}{3x+5}\)

Найдем значение производной в точке \(-1\), т.е. \(f'(-1)\)

Подставляем значение \(x=-1\) в итоговую формулу производной: \(f'(-1)=\frac{3}{3 \cdot (-1) + 5}=1,5\)

Ответ: \(1,5\).

Пример

Исследуем на экстремум функцию \(y=\frac{\ln{x}}{x}\).

Найдем производную заданной функции.
Так как функция \(y=\frac{\ln{x}}{x}\) представляет собой частное двух функций, то используем формулу дифференцирования частного: \[\left(\frac{u}{v}\right)'=\frac{u' \cdot v - u \cdot v'}{v^2}\].

Применив формулу дифференцирования произведения функций, получим: \[y'=\left(\frac{\ln{x}}{x}\right)'=\frac{(\ln{x})' \cdot x - \ln{x} \cdot (x)'}{x^2}=\frac{\frac{1}{x} \cdot x - \ln{x} \cdot 1}{x^2}=\frac{1-\ln{x}}{x^2}\]

Производная \(y'=\frac{1-\ln{x}}{x^2}\) существует при всех значениях \(x>0\), т.е. при всех значениях x из области определения функции.
Значит, критических точек у функции нет.
Найдем стационарные точки.

Стационарные точки, это точки, в которых производная обращается в ноль.
Для нахождения их найдем решение уравнения: \(y'=0\).
Решаем уравнение: \(\frac{1-\ln{x}}{x^2}=0 \Leftrightarrow 1-\ln{x}=0\), то есть \(\ln{x}=1\).
Получим корень: \(x=e\).

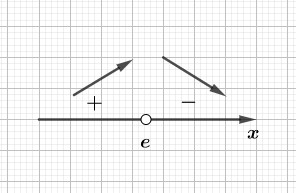
Отмечаем единственную стационарную точку на числовой прямой. Так же отмечаем в полученных промежутках знаки производной.

Для расстановки знаков в каждом промежутке выбираем любое число из этого промежутка и подставляем его в выражение для производной \(\frac{1-\ln{x}}{x^2}\).

Из первого промежутка \(x>e\) возьмем любое число, например, \(e^2\).
Для более простого вычисления выражения \(\frac{1-\ln{x}}{x^2}\) в выбранной точке удобнее брать точку в виде степени числа \(e\).
Подставляем \(e^2\) вместо \(x\) в выражение \(\frac{1-\ln{x}}{x^2}\).
Получим: \(\frac{1-\ln{e^2}}{e^4}=\frac{1-2}{e^4}=-\frac{1}{e^4} < 0\), значит, в первом промежутке имеем знак \(«–»\).
Из второго промежутка \(x < e\) возьмем любое число, например, \(e^{-1}=\frac{1}{e}\).
Подставляем \(e^{-1}\) вместо \(x\) в выражение \(\frac{1-\ln{x}}{x^2}\).
Получим: \(\frac{1-\ln{e^{-1}}}{e^{-2}}=\frac{1-(-1)}{e^{-2}}=\frac{2}{e^{-2}}=2e^2 > 0\), значит, во втором промежутке имеем знак \(«+»\).

Расставляем полученные знаки производной в каждом из промежутков.
Там, где производная функции положительна, функция возрастает. И, наоборот, там, где производная функции отрицательна, функция убывает.
Отобразим поведение функции на каждом из промежутков с помощью стрелок.
Стрелки на рисунке показывают возрастание (знак \(+\)) или убывание (знак \(–\)) функции на указанных промежутках.
Соответственно точка \(x=e\) является точкой максимума (функция меняет поведение с возрастания на убывание).

Найдем экстремальное значение функции: \(y_{max}\).

Подставим в формулу функции точки экстремума: \(y_{max}=f(e)=\frac{\ln{e}}{e}=\frac{1}{e}\).

Ответ: \(y_{max}=\frac{1}{e}\).