Логарифмические неравенства
Логарифмическими неравенствами называют неравенства вида \(\log_af(x)> \log_ag(x)\),
где \(a\) – положительное число, отличное от единицы, а также неравенства, сводящиеся к этому виду.
Если \(f(x) > 0\) и \(g(x) > 0\), то:
- при \(a> 1\) логарифмическое неравенство \(\log_af(x) > \log_ag(x)\) равносильно неравенству того же смысла: \(f(x)> g(x)\).
- при \(0< a < 1\) логарифмическое неравенство \(\log_af(x) > \log_ag(x)\) равносильно неравенству противоположного смысла: \(f(x)< g(x)\).
При \(a> 1\) переходят от неравенства \(\log_af(x) > \log_ag(x)\) к равносильной ему системе неравенств: \[\left\{ \begin{matrix} f(x)> 0 \\ g(x) > 0 \\ f(x) > g(x) \\ \end{matrix} \right.\] а при \(0< a < 1\) – к равносильной неравенству \(\log_af(x) > \log_ag(x)\) системе неравенств: \[\left\{ \begin{matrix} f(x)> 0 \\ g(x) > 0 \\ f(x) < g(x) \\ \end{matrix} \right.\] Первые два неравенства каждой их этих систем определяют ОДЗ переменной для исходного неравенства.
Решим неравенство \(\log_3(2x-4) > \log_3(14-x)\)
Заменяем неравенство равносильной ему системой неравенств.
Основание \(a=3 > 1\), значит, в этом случае знак основного неравенства сохраняется.
Первые два неравенства системы – это ОДЗ:
\(\log_af(x) > \log_ag(x) \Longleftrightarrow \left\{ \begin{matrix} f(x)> 0 \\ g(x) > 0 \\ f(x) > g(x) \\ \end{matrix} \right.\)
Перепишем исходное неравенство в виде равносильной системы:
\(\left\{ \begin{matrix}
2x-4 > 0 \\
14-x > 0 \\
2x-4 > 14-x \\
\end{matrix} \right.\)
Из первого неравенства находим:
\(x > 2\), из второго: \(x < 14\), из третьего: \(x>6\).
Рисуем числовую прямую с отмеченными решениями.
Итоговым решением является пересечение всех трех решений (синий отрезок на рисунке).
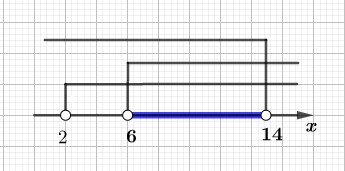
Ответ: \(x \in (6;14)\).
Решим неравенство \(\log_{\frac{1}{3}}(2x-4) > \log_{\frac{1}{3}}(14-x)\)
Заменяем неравенство равносильной ему системой неравенств.
Основание \(a=\frac{1}{3}, 0< a < 1\), значит, в этом случае знак основного неравенства сохраняется.
Первые два неравенства системы – это ОДЗ:
\(\log_af(x) > \log_ag(x) \Longleftrightarrow \left\{ \begin{matrix} f(x)> 0 \\ g(x) > 0 \\ f(x) < g(x) \\ \end{matrix} \right.\)
Перепишем исходное неравенство в виде равносильной системы:
\(\left\{ \begin{matrix} 2x-4 > 0 \\ 14-x > 0 \\ 2x-4 < 14-x \\ \end{matrix} \right.\)
Из первого неравенства находим: \(x > 2\), из второго: \(x < 14\), из третьего: \(x< 6\).
Рисуем числовую прямую с отмеченными решениями.
Итоговым решением является пересечение всех трех решений (синий отрезок на рисунке).
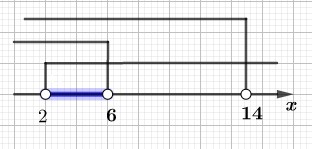
Ответ: \(x \in (2;6)\).
Решим неравенство \(\log_{\frac{1}{2}}(16+4x-x^2) \le -4\).
Приведем неравенство к виду: \(\log_af(x) \le \log_ag(x)\).
Для этого представим в правой части неравенства число \(-4\) в виде логарифма с основанием \(\frac{1}{2}\) (так как в левой части уже стоит логарифм с таким основанием).
По основному логарифмическому тождеству: \(\log_aa^b=b\), поэтому имеем:
\(-4=\log_{\frac{1}{2}}\left(\frac{1}{2}\right)^{-4}=\log_{\frac{1}{2}}2^4=\log_{\frac{1}{2}}16\).
Значит, \(-4=\log_{\frac{1}{2}}=16\), так как \(16=\left(\frac{1}{2}\right)^{-4}\).
Тогда перепишем исходное неравенство в виде: \(\log_{\frac{1}{2}}(16+4x-x^2) \le \log_{\frac{1}{2}}16\).
В \(\log_{\frac{1}{2}}(16+4x-x^2) \le \log_{\frac{1}{2}}16\) основание логарифма равно \(a=\frac{1}{2} < 1 \), значит, в равносильной системе неравенств меняется знак.
Так же заметим, что в данном неравенстве функция \(g(x)\) равна константе и всегда больше нуля, значит, в равносильной системе неравенств будет только два:
\(\log_af(x) > \log_ag(x) \Longleftrightarrow \left\{ \begin{matrix}
f(x)> 0 \\
f(x) \ge g(x) \\
\end{matrix} \right.\)
Решаем равносильную систему неравенств:
\(\left\{ \begin{matrix}
16+4x-x^2 > 0 \\
16+4x-x^2 \ge 16 \\
\end{matrix} \right.\)
Заметим, что если выполняется второе неравенство, то автоматически выполняется и первое, так как \(16 > 0\).
Значит, первое неравенство можно отбросить и решать только второе.
Решая второе неравенство, получим: \(x^2-4 \le 0\)
Неравенство \(x^2 - 4x \le 0 \)– неполное квадратное.
Решаем его методом интервалов.
Разложим левую часть неравенства на множители. Для этого вынесем \(x\) за скобки и получим:
\(x(x-4) \le 0 \)
Отмечаем на координатной прямой корни из каждой скобки: \(x=0\) и \(x=4\).
В полученных трех промежутках расставляем знаки выражения \(x(x-4)\).
Для расстановки знаков в каждом промежутке выбираем любое число из этого промежутка и подставляем его в выражение \(x(x-4)\).
-
Из первого промежутка \(x > 4\) возьмем любое число, например, \(5\).
Подставляем \(5\) вместо \(x\) в выражение \(x(x-4)\).
Получим: \(5 \cdot (5-4) =5 > 0\), значит, в первом промежутке имеем знак \(«+»\). -
Из второго промежутка \(0 < x < 4\) возьмем любое число, например, \(1\).
Подставляем \(1\) вместо \(x\) в выражение \(x(x-4)\).
Получим: \(1 \cdot (1-4)=5 > 0\), значит, во втором промежутке имеем знак \(«–»\). -
Из третьего промежутка \(x< 0\) возьмем любое число, например, \(-2\).
Подставляем \(-2\) вместо \(x\) в выражение \(x(x-4)\).
Получим: \(-2 \cdot(-2-4)=12 > 0\), значит, в третьем промежутке имеем знак \(«+»\).
Расставляем полученные знаки на числовой прямой.
Так как мы решаем неравенство \(x(x-4) \le 0\) то выбираем промежуток со знаком \(«–»\).
Таким образом, решением будет промежуток \([0;4]\).
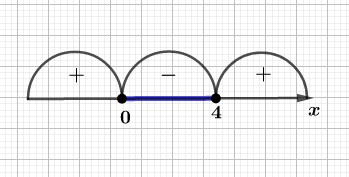
Ответ: \(x \in [0;4]\).
Решим неравенство \(\log x+ \lg (45-x) \le 2 + \lg 2\).
Выпишем из исходного неравенства условия, определяющие ОДЗ.
Все выражения под логарифмами, содержащие переменную \(x\), должны быть положительными. Тогда ОДЗ определяется системой:
\(\left\{ \begin{matrix}
x > 0 \\
45 - x > 0 \\
\end{matrix} \right.\)
Приведем неравенство к виду: \(log_af(x) \le \log_ag(x)\).
Для этого используем в левой и правой части формулу суммы логарифмов:
\(log_ab+\log_ac=\log_abc\)
По формуле суммы логарифмов левую часть перепишем в виде:
\(\lg{x}+\lg{(45-x)}=\lg{x(45-x)}=\lg{(45x-x^2)}\)
В правой части неравенства только один десятичный логарифм. Число \(2\) можно представить в виде десятичного логарифма, используя основное логарифмическое тождество: \(\log_aa^b=b\).
Тогда \(2=\lg10^2=\lg100\).
Получив в правой части сумму логарифмов \(2+\lg2=\lg100 + \lg2\), применим к ней формулу суммы логарифмов:
\(\lg100 + \lg2 = \lg(100 \cdot 2) =\lg200\)
Тогда перепишем исходное неравенство в виде: \(\lg(45x-x^2) \le \lg200\).
В \(\lg(45x-x^2) \le \lg200\) основание логарифма \(a=10 > 1\), значит, в равносильной системе неравенств знак сохраняется.
Запишем равносильную систему неравенств, включающую в себя условия ОДЗ, полученные ранее.
Решаем равносильную систему неравенств:
\(\left\{ \begin{matrix}
x > 0 \\
45 - x > 0 \\
45x - x^2 \le 200 \\
\end{matrix} \right.\)
Два первых неравенства можно записать в виде двойного неравенства: \(0 < x < 45\).
Третье неравенство равносильно неравенству: \(x^2-45x+200 \ge 0\).
Неравенство \(x^2-45x+200 \ge 0\) – квадратное. Решаем его методом интервалов.
Разложим левую часть неравенства на множители. Для этого вычислим корни квадратного уравнения: \(x^2-45x+200=0\).
Это будут числа: \(x_1=40,x_2=5\).
Тогда, согласно тождеству
\(ax^2+bx+c=a(x-x_1)(x-x_2)\)
получим:
\(x^2-45x+200=(x-40)(x-5)\).
Т.е. исходное неравенство равносильно неравенству:
\((x-40)(x-5) \ge 0\).
Отмечаем на числовой прямой корни каждой скобки: \(x=40\) и \(x=5\).
В полученных трех промежутках расставляем знаки выражения \((x-40)(x-5)\).
Для расстановки знаков в каждом промежутке выбираем любое число из этого промежутка и подставляем его в выражение \((x-40)(x-5)\).
-
Из первого промежутка \(x > 40\) возьмем любое число, например, \(50\).
Подставляем \(50\) вместо \(x\) в выражение \((x-40)(x-5)\).
Получим: \(50 -40)(50-5) = 10 \cdot 45 > 0\), значит, в первом промежутке имеем знак \(«+»\). -
Из второго промежутка \(5 < x < 40\) возьмем любое число, например, \(10\).
Подставляем \(10\) вместо \(x\) в выражение \((x-40)(x-5)\).
Получим: \((10-40)(10-5) = -30 \cdot 5 < 0\), значит, во втором промежутке имеем знак \(«–»\). -
Из третьего промежутка \(x< 5\) возьмем любое число, например, \(0\).
Подставляем \(0\) вместо \(x\) в выражение \((x-40)(x-5)\).
Получим: \((0-40)(0-5)= -40 \cdot (-5)= 200 > 0\), значит, в третьем промежутке имеем знак \(«+»\).
Расставляем полученные знаки над каждым промежутком на числовой прямой.
Так как мы решаем неравенство \((x-40)(x-5) \ge 0 \), то решением будут промежутки со знаком \(«+»\).
Таким образом, решением неравенства \((x-40)(x-5) \ge 0 \) будет объединение двух интервалов \((-\infty;5]\cup[40;+\infty)\).
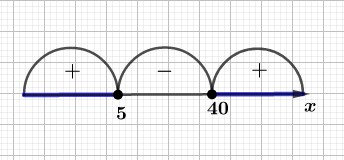
Добавляем на прямую интервал, определяющий ОДЗ: \(0 < x < 45\).
Получим итоговое решение логарифмического неравенства – пересечение двух множеств: \((-\infty;5] \cup [40; +\infty)\) и \((0;45)\).
Это промежуток: \((0;5] \cup [40;45)\).
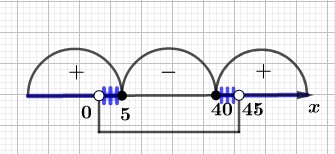
Ответ: \((0;5] \cup [40;45)\).
Решим неравенство \(4\log_2^2x-5\log_2x+1 \le 0\).
Данное неравенство очень похоже на уравнения из предыдущей темы, которые решались методом введения новой переменной.
Первоначально определим ОДЗ неравенства: \(x > 0\).
Вводим новую переменную: \(t=\log_2x\).
Тогда получим неравенство для новой переменной \(t\):
\(4t^2-5t+1 \le 0\)
Неравенство \(4t^2-5t+1 \le 0\) решаем методом интервалов.
Находим корни уравнения:
\(4t^2-5t+1 = 0\)
Корни: \(t_1=1, t_2=\frac{1}{4}\)
Тогда \(4t^2-5t+1 = 4(t-1)(t-\frac{1}{4})\)
Получим равносильное неравенство:
\(4(t-1)(t-\frac{1}{4}) \le 0\)
Наносим корни каждой скобки: значения \(t=1\) и \(t=\frac{1}{4}\) на числовую прямую.
В полученных трех промежутках расставляем знаки выражения \(4(t-1)(t-\frac{1}{4})\).
Для расстановки знаков в каждом промежутке выбираем любое число из этого промежутка и подставляем его в выражение \(4(t-1)(t-\frac{1}{4})\).
-
Из первого промежутка \(t > 1\) возьмем любое число, например, \(2\).
Подставляем \(2\) вместо \(t\) в выражение \(4(t-1)(t-\frac{1}{4})\).
Получим: \(4(2-1)(2-\frac{1}{4}) = 17 > 0\), значит, в первом промежутке имеем знак \(«+»\). -
Из второго промежутка \(\frac{1}{4} < t < 1\) возьмем любое число, например, \(\frac{1}{2}\).
Подставляем \(\frac{1}{2}\) вместо \(t\) в выражение \(4(t-1)(t-\frac{1}{4})\).
Получим: \(4(\frac{1}{2}-1)(\frac{1}{2}-\frac{1}{4}) = \frac{1}{2} < 0\), значит, во втором промежутке имеем знак \(«–»\). -
Из третьего промежутка \(t< \frac{1}{4}\) возьмем любое число, например, \(0\).
Подставляем \(0\) вместо \(t\) в выражение \(4(t-1)(t-\frac{1}{4})\).
Получим: \(4(0-1)(0-\frac{1}{4}) = 1 > 0\), значит, в третьем промежутке имеем знак \(«+»\).
Расставляем полученные знаки над каждым промежутком на числовой прямой.
Так как мы решаем неравенство \(4(t-1)(t-\frac{1}{4}) \le 0\), то выбираем промежутки со знаком \(«–»\).
Таким образом, решением неравенства \(4(t-1)(t-\frac{1}{4}) \le 0\) будет промежуток \([\frac{1}{4};1]\).
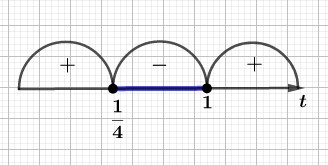
Для того чтобы сделать обратную замену, нам нужно написать соответствующее неравенство по переменной \(t\), в которое мы потом будем подставлять заменяемое выражение \(\log_2x\).
Решение неравенства замены \(t \in [\frac{1}{4};1]\) можно переписать в виде двойного неравенства: \(\frac{1}{4} \le t \le 1\).
В это неравенство мы и будем подставлять заменяемое выражение \(\log_2x\).
Делаем обратную замену в неравенстве \(\frac{1}{4} \le t \le 1\).
Подставляем вместо \(t\) выражение \(\log_2x\), получим неравенство: \(\frac{1}{4} \le t \le 1\).
Представляем и левую и правую часть двойного неравенства в виде логарифма по основанию \(2\).
По основному логарифмическому тождеству \(b=\log_aa^b\) получим:
\(\frac{1}{4}=\log_22^{\frac{1}{4}}, 1 = \log_22\).
Тогда, подставляя в неравенство \(\frac{1}{4} \le \log_2x \le 1\) соответствующие выражения, получим итоговое неравенство: \(\log_22^{\frac{1}{4}} \le \log_2x \le \log_22\).
Так как основания всех трех логарифмах одинаковые и больше \(1\), то мы можем убрать значки логарифмов и сохранить знаки неравенства. Если бы основание логарифмов было бы числом от \(0\) до \(1\), то все знаки неравенства поменялись бы на противоположные.
Получаем неравенство для переменной \(x\):
\(2^{\frac{1}{4}} \le x \le 2\)
Или, с учетом того, что \(2^{\frac{1}{4}}=\sqrt[4]{2}\), получаем ответ: \(\sqrt[4]{2} \le x \le 2\).
Пересекаем решение последнего неравенства с условием ОДЗ: \(x>0\).
Получаем итоговый ответ:
\(x \in [\sqrt[4]{2};2]\)
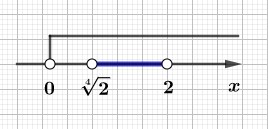
Ответ: \(x \in [\sqrt[4]{2};2]\)
© ООО «Знанио»
С вами с 2009 года.
![]()
