Методика решения расчетных химических задач
Решение расчетных задач по химии очень тесно связано с физикой и математикой. Эти межпредметные связи надо постоянно иметь в виду.
В курсе физики величина «количество вещества» изучается значительно позднее, чем в химии. Поэтому важно правильно сформировать понятие о ней, чтобы в дальнейшем у учащихся не возникало противоречий.
Методику решения задач также полезно связать с физикой, сохраняя форму записи условия и решения. Этого требует и соблюдаемый в школе единый орфографический режим. Кроме того, гораздо более рационален физико-математический путь решения, когда все расчеты производят сначала в буквенных выражениях и лишь после этого подставляют числовые значения.
Традиционная методика обучения решения химических задач (чаще всего — это решение задач методом составления пропорций) имеет ряд недостатков. В результате лишь немногие учащиеся сознательно и творчески овладевают общим подходом к решению, умеют оценивать свои действия в процессе решения, самостоятельно составлять условия задач, умеют выбирать рациональные способы решения и др.
Представленная методика обучения решения задач от общих приёмов к частным позволяет решить недостатки традиционных способов обучения. Мы будем опираться на приёмы решения задач с использованием основных физических величин. Среди них величина n (или v) — количество вещества — позволяет связать все основные физические величины друг с другом. Это даёт возможность составлять логические схемы решения задач с использованием этих физических величин.
Задача учителя состоит в том, чтобы научить учащихся понимать смысл этих физических величин и применять физические формулы при решении расчётных задач различных типов, научить анализировать условия задач через составление логической схемы решения конкретной задачи на основе знания общего подхода к решению. Составление логической схемы задачи предотвращает многие ошибки, которые допускают учащиеся.
Ниже приведены основные формулы физических величин и их взаимосвязи, которые учащиеся должны знать в обязательном порядке и использовать их при решении.
Рассмотрим примеры решения основных типов задач, по которым можно понять методический подход при обучении учащихся.
Исходные формулы, отображающие взаимосвязь физических величин:
- Относительная атомная масса (Ar):
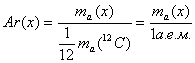 , где x — любой химический элемент.
, где x — любой химический элемент. - Относительная молекулярная масса (Mr):
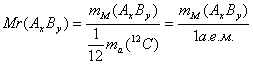 ;
;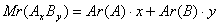 .
. - Плотность вещества (ρ) позволяет связать собой массу (m) и объем (V) вещества:
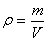 .
. - Масса, объем, число частиц (N), количество теплоты (Q) связаны между собой универсальной физической величиной — количеством вещества — n (или v):
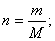
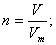
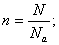
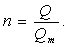
- Относительная плотность (D):
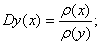
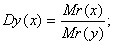
- Массовая доля ω:
элемента в веществе: ![]() ;
;![]() ;
;
примеси в веществе:![]() ;
;
растворенного вещества в растворе: ![]() ;
;
m р-ра = m р.в+ mр-ля
mр-ра=Vр-ра· ρр-ра.
- Объемная доля вещества в смеси (φ) (для газов):
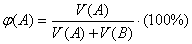 .
. - Молярная концентрация (Сm или С):
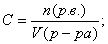
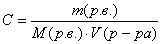 .
. - Уравнение Клапейрона - Менделеева:
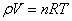 .
.
Методика решения задач различных типов.
Расчеты по химическим формулам.
Решение данного типа задач начинается с осмысления понятия записи химической формулы, с осмыслением того, что учащиеся могут узнать по записи химической формулы. Рассмотрим примеры решения задач с использованием веществ только молекулярного строения. Молекулярная (истинная) формула показывает действительное число атомов каждого элемента в молекуле.
Алгоритм решения базовой задачи:
- Заданный по условиям параметр переводим в количество вещества (n или v;).
- По индексам определяем количество вещества искомого химического элемента (n(х) или v(х)).
- По формулам, отображающим взаимосвязь величин, рассчитываем неизвестный параметр.
Графическая схема решения базовой задачи.
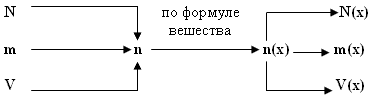
Примеры задач
Задача. Рассчитайте число атомов углерода и кислорода в 11,2 л. (н.у.) углекислого газа.
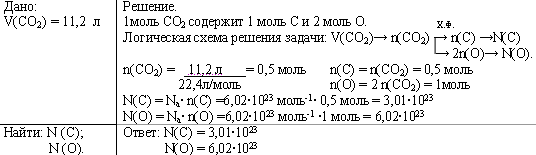
Задача. В каком объеме углекислого газа содержится 9,03·1023 атомов кислорода?
Какова его масса?
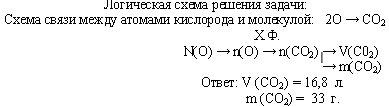
Задача. Газ, плотность которого равна 1,96 г/л (н.у.), состоит из углерода и кислорода, причем ω(C) = 0,27. Определите формулу данного вещества.
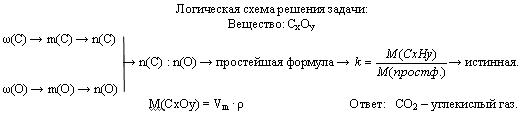
Расчёты по химическим уравнениям
Химическими уравнениями называют условную запись химической реакции посредством химических знаков, формул и коэффициентов.
Уравнение химической реакции показывает, какие вещества вступают в реакцию и какие образуются, а также соотношение количеств этих веществ. Иными словами, химическое уравнение — это способ выражения (передачи) качественной и количественной информации о химическом явлении.
Запишем уравнение реакции в общем виде: aA + bB → cC +dD, где А и В — исходные вещества, С и D — продукты реакции, a, b, c, d — стехиометрические коэффициенты.
Стехиометрические коэффициенты подбирают на основе того, что число атомов каждого элемента до и после реакции остается неизменным. Это можно рассматривать как следствие закона сохранения массы.
Рассмотрим информацию, содержащуюся в стехиометрических коэффициентах. Отношение стехиометрических коэффициентов равно:
- отношению числа частиц, вступивших в реакцию и образовавшихся в результате реакции
a : b : c : d = N(A) : N(B) : N(C) : N(D) - отношению молярных количеств веществ, вступивших в реакцию и образовавшихся в результате реакции
a : b : c : d = n(A) : n(B) : n(C) : n(D) - отношению объемов, вступивших в реакцию и образовавшихся в результате реакции газообразных веществ
a : b : c : d = V(A) : V(B) : V(C) : V(D).
Последнее отношение выполняется, если:
- это газообразные вещества, близкие по свойствам к идеальному газу,
- объемы этих газов измерены при одинаковом давлении и температуре.
Несмотря на большое разнообразие задач данного типа, принцип решения их одинаков: по известному параметру (N, m, V) одного вещества рассчитывается неизвестный параметр X (Nx, mx, Vx) другого вещества. Такая задача является простейшей (базовой).
Алгоритм решения базовой задачи (последовательность действий):
- Составляем уравнение химической реакции и выписываем мольные соотношения прореагировавших и получившихся веществ.
- По формулам, отображающим взаимосвязь физических величин, переводим заданную по условию величину в количество (n или ν) исходного вещества.
- По мольным отношениям рассчитываем n определяемого вещества (Х).
- По формулам, отображающим взаимосвязь физических величин, рассчитываем неизвестный параметр X.
Графическая схема решения базовой задачи.
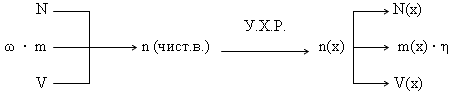
В качестве базовых рассмотрим решение следующих задач:
Задача. Вычислите n, m, V углекислого газа, полученного при действии на 50 г карбоната кальция избытком раствора соляной кислоты.
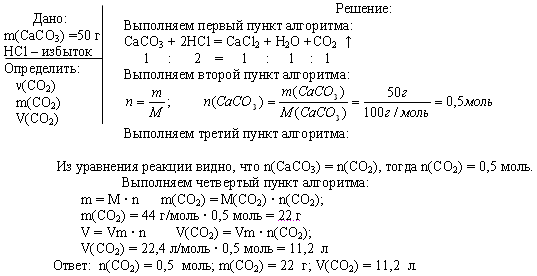
Задача. При взаимодействии цинка с избытком раствора соляной кислоты выделилось 1,12 л водорода (н.у.). Вычислите массы растворившегося цинка и образовавшейся соли.
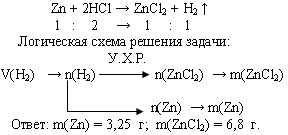
Задача. При взаимодействии с избытком соляной кислоты металла (валентность, которого во всех соединениях равна II) массой 12 г образовался водород объемом 6,72 л (н.у.). Определите, какой это металл.
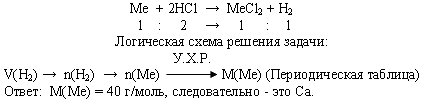
Усложнение базовой задачи.
Расчет массы реагирующих или образующихся химических соединений на практике осложнен. Это обусловлено несколькими причинами:
- Исходные вещества или продукты реакции задаются в условиях отличных от нормальных.
- Исходные вещества вводятся в виде растворов.
- Во многих случаях реагенты содержат примеси, которые в данной конкретной реакции либо не участвуют вообще, либо образуют отличные от целевого продукта вещества.
- Выход продуктов не соответствует теоретическому, т.к. очистка целевого вещества приводит не только к освобождению от многочисленных примесей, но и к частичной потери основного вещества.
Таким образом, перед использованием исходных данных для решения задачи и подстановки их в основную цепь расчетов необходимо провести те или иные дополнительные преобразования. Для перевода условий, отличных от нормальных (для газообразных веществ) используется исходная формула 9 — расчеты физико-химических величин по управлению Клапейрона - Менделеева.
Задача. Сколько граммов 10%-ного раствора гидроксида натрия требуется для нейтрализации 20 г 4,9%-нго раствора серной кислоты?
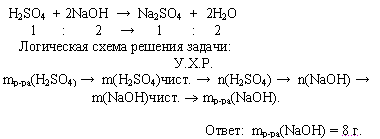
Расчет количественных параметров продуктов реакции, если исходные вещества содержат примеси, расчет массовой доли примеси
Абсолютно чистого вещества в природе не бывает, поэтому в химических производствах вынуждены использовать исходные вещества, содержащие примеси. Эти примеси обычно имеют отличные от основного вещества свойства и, поэтому не образуют в процессе производства нужные продукты.
В связи с этим, чтобы определить количественные параметры получаемого продукта, необходимо вначале рассчитать количественные параметры вступающего в реакцию чистого вещества, которое содержится в исходном объекте. После этого решается базовая задача.
Обратные задачи заключаются в оценке чистоты исходных веществ по количеству продуктов реакции.
Содержание примеси обычно выражают в частях от единицы (или выражают в %). Эта величина показывает массовую долю чистого вещества (примеси) в исходном образе (формула 1).
Для вычисления массы чистого вещества (или примесей), содержащегося в смеси, используют формулу 2.
![]() (1)
(1)
m(смеси) = m(осн.в.) + m(прим.) (2)
Задача. При взаимодействии 10,8 г кальцинированной соды (безводный карбонат натрия) с избытком раствора соляной кислоты получили 2,24 л (н.у.) оксида углерода (IV). Вычислите содержание примеси в соде.
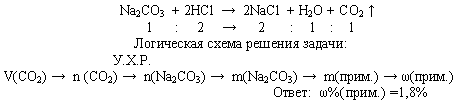
Расчеты по химическим уравнениям, если одно из реагирующих веществ дано в избытке
Как быть, если одновременно заданы параметры нескольких реагирующих веществ? По какому из них вести расчет? Это определяют, сравнения отношения стехиометрических коэффициентов и отношение количеств вещества, взятых для данной реакции.
Если один из реагентов присутствует в количестве больше, чем стехиометрическое, то часть его остается неиспользованной после окончания реакции (избыток вещества). Очевидно, что расчеты нужно вести по веществу, которое в данной реакции расходуется полностью (т.е. находится в недостатке).
Задача. В реакционном сосуде смешали 6,72 л оксида углерода (II) и 2,24 л кислорода и смесь подожгли. Определите объемный состав полученной смеси.
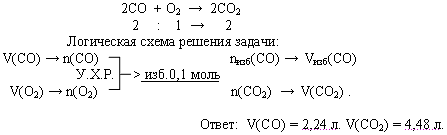
© ООО «Знанио»
С вами с 2009 года.
![]()
