Работа учителя по разработке занятий по подготовке к математическим олимпиадам

Математические олимпиады являются одной из разновидностей математических соревнований. Сегодня олимпиады по признаются наиболее массовой формой внеклассной работы по математике.

Целями проведения олимпиад являются:

• расширение кругозора учащихся;
• развитие интереса учащихся к изучению математики;
• общий подъем математической культуры, интеллектуального уровня учащихся;
• выявление учащихся, проявивших себя в математике, для участия в следующем туре олимпиад и для организации индивидуальной работы с ними;
• знакомство учащихся с важнейшими проблемами и методами современной математики.

Традиционные олимпиады по математике (всероссийская олимпиада школьников) проходят, в настоящее время, в четыре тура: школьный, муниципальный (районный, городской), региональные (областной, краевой, республиканский) и всероссийский.

Данный вид математических соревнований остается самым массовым и популярным как среди учащихся, так и среди педагогов.

Наряду с традиционной системой олимпиад в России в последние годы проводятся и другие олимпиады. К их числу можно отнести олимпиады среди будущих абитуриентов вузов, многоуровневые олимпиады, заочные олимпиады, интернет-олимпиады и др. Олимпиады же готовят учащихся к жизни в современных условиях конкуренции. Причем, главная ценность олимпиад состоит не в выявлении победителей и награждении особо одаренных учащихся, а в общем подъеме математической культуры, интеллектуального уровня учащихся, развитии познавательного интереса.

Организаторам олимпиадного движения необходимо обратить внимание на категорию учащихся 5-8 классов, так как именно в этом возрасте дети наиболее любознательны, желают участвовать в различных соревнованиях. Сегодня практически большинство учащихся этих классов находится вне олимпиадного движения.

Традиционные школьные математические олимпиады

С 2008 года Всероссийская олимпиада школьников по математике проводится в 4 этапа (школьный, муниципальный, региональный и заключительный)

Школьный этап (Первый этап) организует общеобразовательное учреждение.

Математические олимпиады в школе, как правило, проводятся отдельно для каждой параллели классов, начиная с 5 класса. Основными целями школьной олимпиады являются:

• расширение кругозора учащихся;
• развитие интереса учащихся к изучению математики;
• выявление учащихся, проявивших склонность к изучению математики, организация индивидуальной работы с ними.

Школьные математические олимпиады могут проходить в несколько туров. Сначала можно провести олимпиаду классе, затем внутришкольную. Иногда проводят подготовительный тур, чтобы отобрать участников школьной олимпиады. Но целесообразно предоставить возможность участия в школьной олимпиаде каждому желающему. Вопросы организации школьного тура олимпиад вырабатывает оргкомитет школы, в который, как правило, входят: заместитель директора – председатель оргкомитета, председатель школьного методического объединения учителей математики – заместитель председателя оргкомитета, а также члены оргкомитета: учителя математики и представители старшеклассников.

Для составления, проверки и оценки работ участников олимпиады создается жюри, в состав которого входят председатель и члены жюри. Председателем жюри чаще всего является руководитель школьного методического объединения учителей математики. Членами жюри могут быть учителя математики и преподаватели вузов, работающие в данной школе; старшеклассники (для проведения олимпиад в младших классах) и студенты педвузов. Состав оргкомитета, жюри, порядок проведения олимпиад в школе утверждается директором школы.

Время проведения школьных олимпиад определятся в соответствии с Положением о проведении Всероссийской олимпиады в данном учебном году и методическими рекомендациями предметно-методической комиссии по математике.

Председатель оргкомитета собирает оргкомитет и распределяет обязанности для всех членов:

• подготовка олимпиадных заданий;
• разработка положения о проведении олимпиады, поощрении победителей;
• подготовка материалов (бумаги и т.п.);
• подготовка объявления и т.д.

Наиболее ответственным моментом подготовки олимпиады является составление заданий.

Анализ многочисленной литературы по проблеме олимпиадного движения, а также личный опыт участия в олимпиадах различного уровня, опыт составления текстов математических олимпиад, позволяют сформулировать следующие основные требования к тексту школьной олимпиады по математике:

1. Число задач в тексте олимпиадной работы должно быть от 4 до 7 (при 1-3 заданиях могут возникнуть проблемы с определением победителей и призеров олимпиады, настроить на решение больше 7 заданий учащимся сложно).
2. Все задачи в тексте работы должны располагаться в порядке возрастания сложности или трудности.

Сложность – это объективная характеристика задачи, определяемая ее структурой. Сложность задачи зависит от:

• объема информации (числа, понятий, суждений и т.д.), необходимого для ее решения;
• количества данных в задаче и числа связей между ними;
• количества возможных выводов из условия задачи;
• количества непосредственных выводов, необходимых для решения задачи;
• количества взаимопроникновений при решении задачи;
• длины рассуждений при решении задачи;
• общего числа шагов решения, привлеченных аргументов и т.д.

Рассчитать сложность задачи не очень просто, чаще всего учителя интуитивно распределяют задачи по уровню сложности. Но для текстов олимпиадной работы задания берут из разных разделов, некоторые из них нестандартные. Поэтому лучше все же применять понятие трудности задания.

Трудность – субъективная характеристика задачи, определяемая взаимоотношениями между задачей и решающим ее учеником.

Трудность задачи зависит от:

• сложности (сложная задача, как правило, является более трудной для учащихся);
• времени, прошедшего после изучения материала, который встречается в тексте задачи (материал, изученный 1-2 года назад, используемые в задаче факты, которые уже забылись, делают ее трудной для учащихся);
• практики в решении подобного рода задач;
• уровня развития ученика (задача, трудная для ученика общеобразовательного класса, может быть легкой для ученика физико-математического класса);
• возраста учащегося (задача трудная для пятиклассника, может быть легкой для восьмиклассника) и т.д.

Трудность определяется процентом учеников, решивших задачу из числа ее решавших.

Существуют различные формулы для расчета трудности задачи. Рассмотрим наиболее простую из них:

Кт = n/p ∙ 100%

Где Кт – коэффициент трудности, измеряемый в процентах, n – число учащихся, не решивших задачу, p – число учащихся, решавших задачу, в том числе и не приступивших к ней (общее число участников олимпиады).

Пример:

Номер задачи	1	2	3	4	5	6
n	2	6	10	12	16	19
p	20	20	20	20	20	20
Кт	10%	30%	50%	60%	80%	95%

Таким образом, из данных таблицы следует, что 6-я задача наиболее трудная, так как ее решил всего 1 ученик, а 1-я наиболее легкая, ее решили 18 учеников.

Рассмотрим основные требования к составлению текста работы школьной математической олимпиады.

В числе первых должны быть 1-2 задачи, доступные большинству учащихся, т.е. их трудность должна быть примерно 10-30%. Это могут быть обычные задачи продвинутого уровня, аналогичные задачам из контрольных работ, а также на темы, которые не изучаются в школе, но методом логических выводов их должны решить большинство участников. Это необходимо, так как в школьной олимпиаде участвуют все желающие. А участник, не решивший ни одной задачи, теряет уверенность в своих силах, а иногда и интерес к математике. Эти задачи могут содержать изюминку, благодаря которой более сильный ученик решит их быстрее и рациональнее.

В середине текста олимпиады следует поместить 2-3 задачи повышенной трудности. Это могут быть задачи продвинутого уровня из контрольных работ, но с измененными условиями. Их должна решить примерно половина участников, т.е. трудность их будет примерно 40-60%. (Ученик, решивший более трети всех задач, уже может получить поощрение.)

Последние 1-2 задания, которые могут решить единицы, значит, трудность их будет 80-95%. Это задания уровня районных (городских) олимпиад.

Задания должны быть из разных разделов школьного курса математики, но, как правило, на материал, изученный в данном учебном году и во втором полугодии предыдущего года.

В числе заданий могут быть занимательные задачи, задачи-шутки, софизмы, задачи прикладного характера.

Для заинтересованности учащихся в посещении кружков, факультативов желательно включать задания, аналогичные рассмотренным там. Это могут быть логические задачи, задачи на применение принципа Дирихле, инвариантов, графов, задачи на раскраски, уравнения в целых числах и т.п. Такого рода задачи часто называют специальным термином «олимпиадные», хотя, конечно, не только они должны быть в тексте школьной олимпиады.

В задачах не должно быть длинных выкладок, трудно запоминающихся формул, необходимости использования справочных таблиц.

Для разных классов могут быть одинаковые задания.

В соответствии Министерства образования и науки РФ № 1252 от 18.11.2013, школьный этап олимпиады проводится по олимпиадным задачам, разработанным предметно-методической комиссией олимпиады, которые готовят и направляют организаторам школьного и муниципального этапов олимпиады методические рекомендации по разработке требований к организации и проведению школьного и муниципального этапов олимпиады по каждому общеобразовательному предмету, определяющие принципы составления олимпиадных заданий и формирования комплектов олимпиадных заданий, описание необходимого материально-технического обеспечения для выполнения олимпиадных заданий, перечень справочных материалов, средств связи и электронно-вычислительной техники, разрешенных к использованию во время проведения олимпиады, критерии и методики оценивания выполненных олимпиадных заданий, процедуру регистрации участников олимпиады, показ олимпиадных работ, а также рассмотрения апелляций участников олимпиады;

Приведем примеры тем олимпиадных задач по математике (школьный этап)

5 класс

1. Арифметика
2. Числовой ребус
3. Задача на построение примера (разрезание фигур, переливания, взвешивания).
4. Логические или текстовые задачи.

6 класс

1. Арифметика (дроби, числовые ребусы).
2. Задача на составление уравнения.
3. Фигуры, нахождение многоугольника с указанными свойствами.
4. Логическая задача.

7 класс

1. Числовой ребус.
2. Задача на составление уравнений.
3. Делимость натуральных чисел. Признаки делимости.
4. Задача на разрезание фигур.
5. Логическая задача.

8 класс

1. Нахождение числа с указанными свойствами.
2. Построение графиков функций.
3. Преобразование алгебраических выражений.
4. Основные элементы треугольника.
5. Логическая задача на четность.

9 класс

1. Делимость, четность.
2. Квадратный трехчлен. Свойства его графика.
3. Основные элементы треугольника.
4. Алгебра (неравенство или задача на преобразование алгебраических выражений).
5. Логическая (комбинаторная) задача.

10 класс

1. Нахождение числового множества, обладающего указанными свойствами.
2. Прогрессии.
3. Площадь. Подобие фигур.
4. Система уравнений.
5. Логическая (комбинаторная) задача.

11 класс

1. Рациональные и иррациональные числа.
2. Тригонометрические уравнения.
3. Окружность. Центральные и вписанные углы.
4. Многоугольники.
5. Комбинаторика.

Это совсем не значит, что в олимпиаде для 5 не могут встретиться задачи на графы или комбинаторные. Поэтому тексты школьной олимпиады лучше все же составлять в школе, учитывая рекомендации предметно-методической комиссии муниципального этапа Олимпиады или внося в рекомендованные ими тексты изменения.

Для составления олимпиадных заданий учреждение образования может привлечь специалистов в области диагностики из вузов или поручить наиболее опытному из учителей. Но, вероятно, лучше, если набираться опыта в составлении текстов будут все учителя. Тем более что после проведения олимпиады уже можно оценить качество подготовленных материалов, а трудность некоторых заданий определить, дав аналогичные задания в классе старше.

Таким образом, составление текстов для каждой параллели можно поручить 1-2 учителям. Они организуют подбор заданий, причем первоначально заданий необходимо подготовить больше.

Окончательные тексты школьных олимпиад желательно утвердить на заседании школьного методического объединения учителей математики, обговорив там число предлагаемых заданий, вариант оценки заданий, распределение членов жюри по классам. Особенно это важно для тех школ, где учащиеся в различных классах обучаются по разным учебникам.

Рассмотрим задачи, которые можно предложить учащимся для подготовки к олимпиаде в школе, городе (районе). Часть данных задач может быть применена в качестве заданий школьных олимпиад. Некоторые из задач 5 класса могут быть использованы в 6, из 6 класса — в 7 и т. д.

В случае, если некоторый материал окажется неизученным на момент решения предлагаемых задач, их можно решить и позже.

Задачи по классам распределены в соответствии с действующими на сегодня наиболее распространенными в общеобразовательных учреждениях учебниками математики, геометрии, алгебры и начал анализа. Особенностью данной подборки является то, что задачи не сгруппированы по разделам, темам. Этой цели служат многие пособия, например, А.В. Фаркова «Математические кружки в школе. 5-8 классы», «Учимся решать олимпиадные задачи. Геометрия. 5-11 классы», А.А. Гусева «Математический кружок 5 класс» «Математический кружок 6 класс» и др.

Предлагаемые задачи заимствованы из различных сборников задач по подготовке к математическим олимпиадам

5 класс

5.1. Напишите число 100:

а) шестью одинаковыми цифрами;

б) девятью различными цифрами.

(Можно использовать знаки: +, :.)

Решение:

а) 99 + 99 : 99; б) 91 + 5742 : 638

5.2. Ваня задумал число, прибавил к нему 5, потом разделил сумму на 9, умножил на 4, отнял 6, разделил на 7 и получил 2. Какое число задумал Ваня?

Решение:

Рассуждая с конца, имеем: 2 ⋅ 7 = 14, 14 + 6 = 20, 20 : 4 = 5, 5 ⋅ 9 = 45, 45 - 5 = 40. Ваня задумал число 40

5.3. Говорил дед внукам: «Вот вам 130 орехов, разделите их на 2 части так, чтобы меньшая часть, увеличенная в 4 раза, равнялась бы большей части, уменьшенной в 3 раза». Как разделить орехи?

Решение:

Уменьшив втрое количество орехов в большей части, мы получим их столько же, сколько в 4 меньших частях. Значит, большая часть должна содержать в 3 ⋅ 4 = 12 (раз) больше орехов, чем меньшая, а общее число орехов должно быть в 13 раз больше, чем в меньшей части. Поэтому меньшая часть должна содержать 130 : 13 = 10 (орехов), а большая: 130 - 10 = 120 (орехов).

5.4. Крестьянин попросил взять у царя 1 яблоко из его сада. Царь разрешил. Пошел крестьянин к саду и видит: весь сад огорожен тройным забором, причем каждый забор имеет одни ворота, вход в которые охраняет сторож. Подошел крестьянин к первому сторожу и говорит: «Царь разрешил мне взять одно яблоко из сада». На что сторож ему сказал: «Возьми, но при выходе отдашь мне половину тех яблок, что возьмешь, и еще одно». Эти же слова повторили крестьянину 2 и 3 сторожа, охранявшие другие ворота. Сколько яблок должен взять крестьянин, чтобы после того, как он отдаст положенную часть 3 сторожам, у него осталось одно яблоко?

Решение:

Задача имеет различные способы решения. Например, для того, чтобы пройти через ворота с яблоками, перед воротами у крестьянина должно быть 2(а +1) яблок. Поэтому перед последними воротами у него должно быть 4 яблока (а = 1), перед вторыми 10 яблок (а = 4), перед первыми 22 яблока (а = 10). Значит, надо взять 22 яблока.

5.5. Запишите число, состоящее из суммы 11 тысяч, 11 сотен и 11 единиц.

Решение: 12111 = 11000 + 1100 + 11

5.6. Объясните, как с помощью спичек можно получить на столе угол в 60°, 90°, 120°. Изобразите получившиеся фигуры с этим углом.

Решение:

Равносторонний треугольник дает угол в 60°, правильная четырехугольная пирамида, у которой все 8 ребер равны 1 спичке, дает в основании квадрат с углом 90°. Два равносторонних треугольника, имеющих общую сторону, дают угол в 120°.

5.7. Сколько существует двузначных чисел, у которых цифра десятков больше цифры единиц?

Ответ: 45

5.8. Школьники Петя и Вася взвесили свои портфели на весах. Весы показали 3 кг и 2 кг. Когда же они поставили на весы оба портфеля, весы показали 6 кг. «Как же так? — удивился Петя. — Ведь 2 + 3 не равняется 6». На что Вася ответил: «Разве ты не видишь, что у весов сдвинута стрелка?» Сколько же весят портфели на самом деле?

Ответ: 3кг и 4 кг.

5.9. Имеются двое песочных часов: на 3 минуты и на 7 минут. Яйцо варится 11 минут. Как отмерить это время при помощи имеющихся часов?

Решение:

Перевернуть двое часов. Когда пройдет 3 минуты, в семиминутных часах останется 4 минуты. Поставить яйцо в данный момент вариться. Когда 4 минуты закончатся, перевернуть семиминутные часы обратно. Получим 4 + 7 = 11.

5.10. В ящике лежат шары: 5 красных, 7 синих и 1 зеленый. Сколько шаров надо вынуть, чтобы достать 2 шара одного цвета?

Ответ: 4

5.11. Николай с сыном и Иван с сыном были на рыбалке. Николай поймал столько же рыб, сколько и его сын, а Иван — втрое больше, чем его сын. Всего было поймано 35 рыб. Сколько рыб поймал Иван и как звали его сына?

Ответ: Иван поймал 21 рыбу, его сына звали Николай.

5.12. Найдите ошибку в следующих рассуждениях. Имеем числовое равенство: 4:4 = 5:5. Вынесем за скобки в каждой части общий множитель. Получим: 4(1:1) =5(1:1). Числа в скобках равны, поэтому 4=5, или 2x2 = 5.

Решение:

Ошибка допущена в вынесении общего множителя за скобки в левой и правой частях тождества 4:4 = 5:5.

5.13. Петя сказал друзьям: «Позавчера мне было 10 лет, а в будущем году исполнится 13». Мог ли Петя не соврать?

Решение:

Да, если это было сказано 1 января, то 30 декабря Пете было 10 лет, 31 декабря исполнилось 11 лет. 31 декабря этого же года ему будет уже 12 лет, а в будущем году — 13.

5.14. Трое учеников пошли на рыбалку, взяв с собой лодку, выдерживающую нагрузку до 100 кг. Как перебраться ученикам с берега реки на остров, если их массы равны 40 кг, 50 кг, 70 кг?

Решение:

План действий должен быть такой:

1. сначала переправляются двое легких,
2. один из них перегоняет лодку обратно,
3. самый тяжелый садится в лодку и переплывает один,
4. второй легкий садится в лодку и перегоняет ее обратно,
5. двое легких садятся в лодку и переправляются на

остров.

5.15. На школьной олимпиаде по математике участникам было предложено решить 6 задач. За каждую решенную задачу засчитывалось по 7 очков, а за каждую нерешенную списывалось 3 очка. Сколько задач решил участник, если он набрал 12 очков? 2 очка? 32 очка?

Решение:

Воспользуемся таблицей подсчета очков

Решено задач	6	5	4	3	2	1	0
Не решено задач	0	1	2	3	4	5	6
Набрано очков	42	32	22	12	2	-8	-18

В результате получим 3 задачи, 2 задачи, 5 задач.

5.16. Решите уравнение .

Ответ: 22

5.17. Какой фигурой может быть пересечение треугольника и четырехугольника? Покажите на рисунках.

Решение: Пересечением может быть точка, отрезок, треугольник, четырехугольник, пятиугольник, шестиугольник, семиугольник или пустое множество (см. рис. 1).

Рис.1

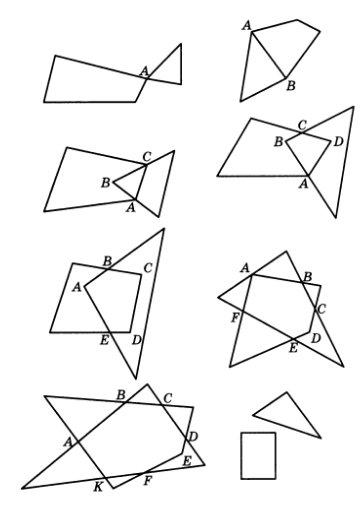
5.18. Почтальон Печкин разнес почту во все дома деревни, после чего зашел к дяде Федору выпить молока. На рис. 2 показаны все тропинки, которые проходил Печкин, причем, как оказалось, ни по одной из них он не проходил дважды. Каков мог быть маршрут почтальона Печкина? В каком доме живет дядя Федор?

Рис. 2

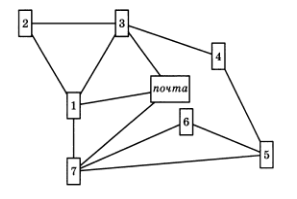
Решение:

Почта — 1 — 3 — почта —7 — 1 — 2 — 3 — 4 — 5 —

б — 7 — 5. Федор живет в доме № 5 (см. рис. 2).

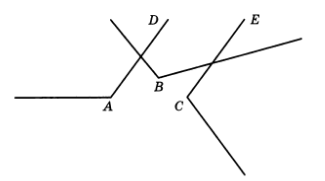
5.19. Начертите три тупых угла так, чтобы два из них не имели общих точек, а стороны третьего пересекали бы лишь одну сторону каждого из первых двух углов.

Решение:

Рис.3

5.20. Ваня шепнул на уроке Марине: «Ижаксдоп тевто!». На каком «языке» говорил Коля? (Оказывается, торговцы вразнос на Руси также знали этот «язык».)

Ответ: Ваня шепнул: «Подскажи ответ», то есть прочитал слова не с начала, а с конца.

6 класс

6.1. Лошадь может съесть воз сена за 1 месяц, коза — за 2 месяца, а овца — за 3 месяца. За какое время лошадь, коза и овца вместе съедят такой же воз сена?

Решение:

За один год лошадь съест 12 возов сена, коза — б, а овца — 4 воза сена. Всего за год они вместе съедят 22 воза сена. Тогда один воз сена они съедят все вместе за

6.2. Найдите дробь со знаменателем 19, которая больше  но меньше

Ответ:

6.3. Сколькими нулями оканчивается произведение: 1 ⋅ 2 ⋅ 3 ... 2001 ⋅ 2002 ⋅ 2003?

Решение:

У числа А =1-2-3 2001 ⋅ 2002 ⋅ 2003 на 5 делится 2000 : 5 = 400 чисел, из них на 25 делится 2000 : 25 = 80 чисел, на 125 делится 2000 : 125 = 16 чисел, на 625 делятся 3 числа. 400 + 80 + 16 + 3 = 499. Тогда число А делится на 5⁴⁹⁹. Так как среди множителей числа А содержится 1001 четных чисел, то А делится и на 2⁴⁹⁹, а значит, А делится на 10⁴⁹⁹, то есть оканчивается 499 нулями.

6.4. 12 человек несут 12 буханок хлеба. Каждый мужчина несет по 2 буханки хлеба, женщина — по  буханки, а ребенок по . Сколько было мужчин, женщин, детей?

Решение:

Так как мужчин не больше б, то самое большее их может быть 5. Значит, мужчины несут 10 буханок. Остается 2 буханки, поэтому 2 женщин не может быть, значит, женщин — 1, а детей — 6.

6.5. На озере расцвела 1 лилия. Каждый день число цветков удваивалось, и на 10-й день все озеро покрылось цветами. На какой день покрылась цветами половина озера?

Ответ: на девятый день.

6.6. Как раз делить круг тремя прямыми на 4,5,6, 7 частей?

Решение:

Рис.4

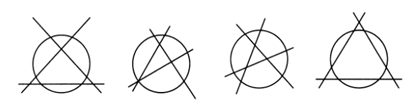
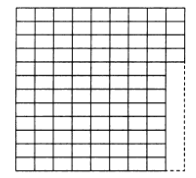
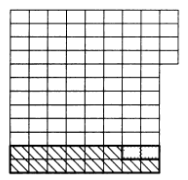
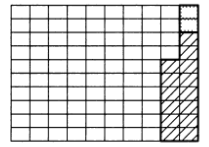
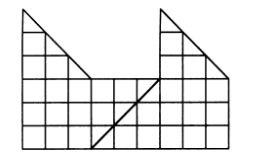
6.7. У Ивана-царевича был волшебный ковер-самолет размером 9х12м², Змей Горыныч подкрался и отрезал от ковра маленький коврик размером 1х8 м². Иван-царевич очень расстроился, т. к. волшебный ковер-самолет мог летать, лишь имея прямоугольную форму. Поэтому он решил еще отрезать кусок 1х4 м², чтобы получился прямоугольник 8х12м², но Василиса Премудрая предложила поступить по-другому. Она разрезала ковер на три части, из которых волшебными нитками сшила квадратный ковер-самолет размером 10х10м². Как переделала ковер Василиса Премудрая?

Решение:

На рис. 5 показан ковер-самолет после того, как его испортил Змей Горыныч. На рис. 6 показан ковер-самолет, который разрезала Василиса Премудрая. На рис. 7 показан ковер-самолет, который сшила Василиса Премудрая.

Рис.5Рис.6Рис.7

6.8. Когда Гулливер попал в Лилипутию, то обнаружил, что там всё ровно в 12 раз короче, чем на его родине. Сможете ли вы сказать, сколько лилипутских спичечных коробков помещается в спичечной коробке Гулливера?

Решение: В гулливерском спичечном коробке должно поместиться 12 лиллипутских коробков в ширину, 12 — в длину, 12 — в высоту. Всего 12 ⋅ 12 ⋅ 12 = 1728 (коробков).

6.10. Имеются чашечные весы без гирь и 3 одинаковые по внешнему виду монеты. Одна из монет фальшивая, причем неизвестно, легче она настоящих монет или тяжелее (одинаковы монеты одного веса). Сколько надо сделать взвешиваний, чтобы определить фальшивую монету? Решите эту же задачу в случаях, когда имеется 4 монеты и 9 монет.

Ответ: 2;2;3

6.11. Плоскость раскрашена в 2 цвета. Докажите, что найдутся 2 точки на расстоянии 1 метр друг от друга, окрашенные в одинаковый цвет.

Решение:

Рассмотрим на плоскости треугольник, все стороны которого равны по 1 метру. По принципу Дирихле, из трех вершин треугольника две каких-то будут окрашены одинаково.

6.12. Имеется 5 закрытых чемоданов и 5 ключей к ним. При этом неизвестно, к какому чемодану подходит какой ключ. Какое наименьшее число попыток надо сделать, чтобы наверняка определить, какой ключ подходит к какому чемодану?

Решение:

Будем первым ключом открывать по очереди все чемоданы. Если один из чемоданов открылся — прекрасно, отставляем в сторону этот чемодан с этим ключом. Если среди первых четырех чемоданов ни один не открылся, то этот ключ непременно будет соответствовать пятому чемодану. Таким образом, мы использовали не более четырех попыток. С оставшимися четырьмя чемоданами и четырьмя ключами поступаем аналогично. Таким образом, мы получим, что понадобится 4 + 3 + 2 + 1 = 10 (попыток).

6.13. На волшебной яблоне выросли 3 банана и 4 апельсина. Если сорвать один из плодов — вырастет такой же; если одновременно 2 одинаковых плода — вырастет апельсин, а если одновременно сорвать 2 разных плода — вырастет банан. В каком порядке надо срывать плоды, чтобы на яблоне остался ровно один? Можно ли определить, какой это будет плод? Можно ли срывать плоды так, чтобы на яблоне ничего не осталось?

Решение:

Рассмотрим, что будет получаться в каждом из различных случаев. Если сорвать банан, на дереве снова вырастет банан. Если сорвать апельсин, снова вырастет апельсин. Т.е если срывать по одному плоду, ничего не меняется. Сорвем 2 банана, тогда на дереве будет 1 банан и 5 апельсинов, т. е. плодов стало на 1 меньше, бананов уменьшилось, апельсинов увеличилось. Больше по 2 банана не сорвать. Сорвем 2 апельсина, на дереве останется 3 банана и 3 апельсина. Сорвем банан и апельсин, тогда на дереве будет 3 банана и 3 апельсина. Таким образом, срывая по 2 плода, мы получаем, что число плодов уменьшится на 1, причем число бананов остается все время нечетным. Можно предложить такой вариант для ответа на 1 вопрос: срывать 4 раза по банану и апельсину вместе, в итоге останется лишь 1 банан. Так как на яблоне всегда остается один плод, то не сделать так, чтобы ничего не осталось.

6.15. Проехав половину всего пути, пассажир лег спать и спал до тех пор, пока не осталось проехать половину того пути, который он проспал. Какую часть всего пути пассажир проехал бодрствующим?

Решение:

Изобразим путь пассажира отрезками (см. рис. 8).

Рис.8

Обозначим за S длину отрезка CD, тогда ВС = 2S (пока спал), всего BD = 3S, но АВ = BD, значит, AD = 6S. Бодрствовал он на АВ и CD, АВ + CD = 3S + S = 4S. Пассажир бодрствовал  (пути).

6.16. Отличник Вася решил купить себе в магазине одну ручку за 1 руб 80 коп и 6 стержней. Продавец потребовал с Васи 5 руб, на что Вася ответил тому, что он ошибся. Прав ли Вася и почему?

Решение:

Да, так как 5 руб—1 руб 80 коп = 3 руб 20 коп = 320 коп; а 320 не делится на б нацело.

6.17. Дима с собакой пошел встречать папу. Когда собака увидела папу, она побежала к нему со скоростью 5 м/с. Добежав до него, она сразу же побежала обратно к Диме. Добежав до Димы, собака снова побежала к папе и т. д. Какое расстояние пробежала собака, если Дима и папа двигались со скоростью 1,5 м/с, а первоначальное расстояние между ними было равно 300 м?

Решение:

Так как Дима и папа двигались со скоростью каждый по 1,5 м/с, то скорость сближения будет равна 3 м/с и они встретятся через 300 м : 3 м/с = 100 с. Т. к. скорость собаки 5 м/с, то за 100 с она пробежит 500 м.

6.18. Вычислите:

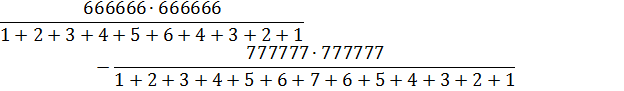
Решение: Найдя значения знаменателей и сократив первую дробь на 6 ⋅ 6, а вторую на 7 ⋅ 7, получим: 111111² - 111111² = 0

6.19. Если треть числа разделить на его семнадцатую часть, в остатке будет 100. Найдите это число.

Решение: Так как у числа есть треть и семнадцатая часть, то оно делится на 51, т. е. имеет вид 51x. Тогда треть его будет 17x:, а семнадцатая часть — Зx . По условию задачи составим уравнение: 17x = 3px + 100. Выразим х:  Учитывая, что x и p натуральные, подбором найдем p=5. Тогда x = 50.

В итоге получим, что число будет 2550.

6.19. Сумма 2008 натуральных чисел — нечетное число. Каким числом, четным или нечетным, является произведение этих чисел?

Решение:

2002 натуральных чисел могут быть все четными; все нечетными; или четными и нечетными. Два первых случая не могут быть, так как сумма — нечетное число. Значит, среди 2002 натуральных чисел есть четные и нечетные числа, поэтому произведение будет числом четным.

6.20. Разрежьте изображенную на рис. 9 фигуру на две одинаковые части.

Рис. 9

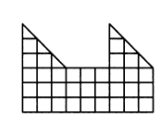
Решение:

Рис.10

6.21 В какой системе счисления справедливо равенство: 4 ⋅ 13 = 100

Решение:

В шестеричной системе счисления.

7 класс

7.1. В классе 25 учеников, а сумма их возрастов составляет 270 лет. Найдутся ли в классе 20 учащихся, сумма возрастов которых больше 260?

Решение:

Пусть такие 20 учащихся найдутся. Тогда сумма возрастов оставшихся 5 учеников будет не больше 10 лет. То есть средний возраст этих «учеников» должен быть не больше 2 лет, что противоречит возрасту учащегося школы (меньше 5 лет возраст ученика быть не может). Таким образом, таких учащихся не найдется.

7.2. Изменится ли частное и остаток, если делимое и делитель увеличить в 3 раза?

Решение:

Так как a = bq + r, то 3a = 3bq + 3r. Значит, остаток увеличился в 3 раза, а частное не изменилось.

7.3. Улитка ползает по столбу высотой 10 м. За день она поднимается на 5 м, а за ночь опускается на 4 м. За какое время улитка доберется от подножия до вершины столба?

Решение:

К концу первых суток улитка поднимется на 1 м, к середине вторых суток — на б м, к середине 3-х — на 7 м.,к середине 5-х — на 9 м, к середине б-х — на 10 м. Таким образом, ответом будет 5,5 суток.

7.4. Сколько раз в сутки часовая и минутная стрелки образуют прямой угол?

Решение:

Условию отвечает положение стрелок в 3 часа, в 9 часов, в 15 часов, в 21 час. Также условие будет сохраняться через поворот часовой стрелки по циферблату на  полного угла. Таким образом, всего за сутки таких положений будет

11 ⋅ 4=44.

7.5. Переписывая с доски числовое выражение a⁵ ⋅ b², ученик допустил ошибку и был очень удивлен, когда выяснилось, что записанное им число a5b2 является значением заданного выражения. Какими могут быть цифры a и b?

Решение:

а = 2, b = 9. Другие варианты не подходят.

7.6. На соревнованиях по фигурному катанию все 9 судей поставили за технику исполнения и артистизм спортсмена только оценки 5,6 и 5,7. Сумма всех оценок оказалась равной 101,9. Сколько оценок 5,7 получил спортсмен?

Ответ: 11

7.7. Для проведения водопровода в дом нужно 167 м труб. В наличии имеются трубы лишь длиной 5 м и 7 м. Сколько надо взять тех и других труб, чтобы сделать наименьшее число соединений?

Ответ: Надо взять 21 трубу длиной по 7 м и 4 трубы длиной по 5 м.

7.8. Жители трех домов решили вырыть общий колодец так, чтобы от каждого дома до колодца было одинаковое расстояние. Покажите на рис. 11, где нужно расположить колодец?

Рис.11

Решение:

Колодец надо вырыть в центре окружности, проходящей через три указанные точки.

7.9 Пришел Иван-царевич в подземелье к Кощею Бессмертному Василису Прекрасную освобождать. В подземелье три темницы. В одной из них томится Василиса, в другой расположился Змей Горыныч, а третья темница — пустая. На дверях есть надписи, но все они ложные. На первой темнице написано: «Здесь Василиса Прекрасная»; на второй темнице: «Темница № 3 не пустая»; на третьей темнице написано: «Здесь Змей Горыныч». В какой же темнице Василиса?

Решение:

Василиса Прекрасная не может быть в первой темнице, значит она во второй или третьей темнице. Так как темница 3 — пустая, то Василиса Прекрасная будет во второй темнице.

7.10. Докажите, что 13 + 13² + 13³ + ... + 13²⁰⁰⁹ + 13²⁰¹⁰ делится нацело на 7.

Решение: 13 + 13² + 13³ + ... + 13²⁰⁰⁹ + 13²⁰¹⁰ = 13 (1 + 13) + 13² (1 + 13) + ... + 13²⁰⁰⁹ (1 + 13) = 14 (13 + 13² + 13³ ... +13²⁰⁰⁹)

Так как 14 делится на 7, то и само число делится нацело на 7.

7.12. Расставьте в записи 4 ⋅ 12 + 18 : 6 + 3 скобки таким образом, чтобы получилось:

а) число 50;

б) возможное наименьшее число;

в) возможное наибольшее число.

Решение:

а) 4 ⋅ 12 + 18 : (6 + 3);

б) 4 ⋅ (12 + 18 : 6 + 3);

в) (4 ⋅ 12 + 18) : (6 + 3).

7.13. 101 лошадь разместили в 15 конюшнях. Почему хотя бы в одной конюшне будет обязательно нечетное число лошадей?

Решение:

Докажем задачу методом от противного. Пусть в каждой конюшне находится четное число лошадей, тогда сумма четных чисел — число четное. А по условию всего лошадей 101 — число нечетное. Таким образом, получили противоречие. Значит, хотя бы в одной конюшне будет нечетное число лошадей.

7.14. Из куба 3x3x3 удалили центральный кубик и восемь угловых кубиков. Можно ли оставшуюся фигуру из 18 кубиков составить из 6 брусков 3x1x1?

Решение: Можно

Рис.12

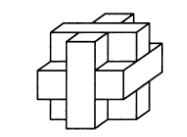
7.15. За два года предприятие снизило объем выпускаемой продукции на 51%. При этом каждый год объем продукции снижался на одно и то же число процентов. На сколько?

Решение: Пусть ежегодно выпуск продукции снижался на х %. Примем первоначальный объем продукции за 1. Тогда через год продукции будет выущено  a через два года — . По условию это число равно , откуда и x = 30

7.16. Во всех подъездах дома одинаковое число этажей, и на каждом этаже одинаковое число квартир. При этом число квартир на этаже меньше числа этажей, но больше числа подъездов, а число подъездов больше одного. Сколько в доме этажей, если всего в доме 60 квартир?

Решение: Обозначим число подъездов в доме, квартир на этаже и число этажей соответственно за х, у, г. Разложим 60 на простые множители: 60 = 2 ⋅ 2 ⋅ 3 ⋅ 5. Так как подъездов больше одного и меньше, чем число квартир и число этажей, то их может быть 2 или 3. Составляя произведение из трех множителей, каждый из которых больше предыдущего, а произведение равно 60, получим следующие варианты: 60 = 2 ⋅ 3 ⋅ 10 = 2 ⋅ 5 ⋅ 6 = 3 ⋅ 4 ⋅ 5. А это означает, что в доме может быть 5, 6 или 10 этажей.

7.17. Существует ли такое натуральное число n, что число 2⁶ + 2⁹ +2ⁿ является полным квадратом?

Решение: Да, например, n = 10,2⁶ + 2 ⋅ 2⁸ + 2¹⁰ = (2³ + 2⁵)²

7.18. В треугольнике ABC угол А равен 40°, угол В равен 20°, а AB-BC = 4. Найдите длину биссектрисы угла С.

Решение: Выполним дополнительное построение: отложим на стороне АВ отрезок BD = ВС и соединим точки D и С (см. рис. 13). Тогда треугольник BCD будет равнобедренным. Поэтому углы DCB и CDB будут равны 80°. Пусть СЕ — биссектриса треугольника ABC. Так как угол C = 120°, то угол ACE = 60°.

Рис.13

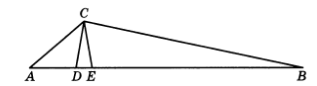
Поэтому угол АЕС = 80°. Таким образом, в треугольнике DEC два угла равны 80°, поэтому он будет равнобедренным. Тогда угол при вершине С данного треугольника будет равен 20°, поэтому угол ACD = 60°-20° = 40°. Значит, треугольник АСD также является равнобедренным, поэтому СЕ = CD = AD = AB-BC = 4.

7.19. Одновременно были зажжены две свечи одинаковой длины: одна потолще (сгорающая за 4 часа), другая потоньше (сгорающая за 2 часа). Через некоторое время обе свечи были потушены. Оказалось, что огарок толстой свечи в 3 раза длиннее огарка тонкой свечи. Сколько времени горели свечи?

Решение:

Обозначим за х часов — время горения свечей. Тогда сгорело  толстой свечи и  тонкой свечи. Так как огарок толстой свечи длиннее огарка тонкой свечи в 3 раза, то получим уравнение:

Решением данного уравнения будет x = 1,6 (часа). Таким образом, свечи горели 1 час 36 минут.

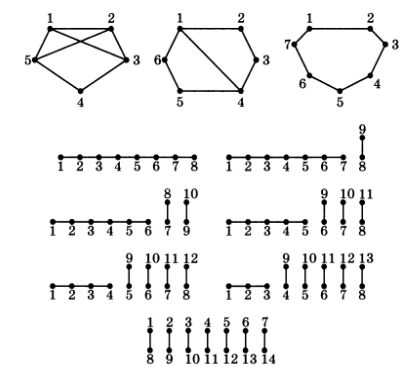
7.20. В некотором государстве имеется несколько городов. Из каждого города выходит хотя бы одна дорога, и между любыми двумя городами не больше одной дороги. Сколько городов может быть в этом государстве, если дорог всего 7?

Решение:

Определим наименьшее и наибольшее число городов в данном государстве. Если в государстве 4 города, то, соединяя все города, получим б дорог. При меньшем числе городов дорог будет еще меньше. Таким образом, наименьшее возможное число городов может быть 5. Теперь оценим число городов сверху. Так как каждая дорога соединяет 2 города, а дорог — 7, то больше 14 городов быть не может. Таким образом, в этом государстве может быть от 5 до 14 городов. Возможные расположения дорог между городами показаны на рис. 14) (цифрами обозначены города).

Рис.14

8 класс

8.1. Постройте треугольник по трем медианам.

Решение:

Возможный план построения:

1. Строим вспомогательный треугольник АОО₁ такой, что
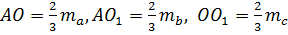
2. Проведем медиану из вершины А, удвоим ее и получим АВ — основание исходного треугольника.
3. Удвоим отрезок О₁О, получим О₁С. Точка С будет третьей вершиной треугольника ABC.

8.2. Какой знак следует поставить между дробями  и , чтобы в результате получить дробь  равную каждой из дробей и ?

Ответ. Знак «=»

8.3. Можно ли разрезать разносторонний треугольник на два равных треугольника?

Решение:

Пусть АВС разрезан на 2 равных треугольника (см. рис. 15). Тогда угол ADB в ADB должен быть равен одному из углов АОС. Но угол ADB не может равняться углу ACD или углу CAD, так как внешний угол треугольника всегда больше внутреннего угла треугольника, не смежного с ним. Если же угол ADB = углу ADC, то угол ADB = углу ADC = 90°, значит, AD является высотой. Но в равных треугольниках против равных углов лежат равные стороны, значит, АВ = АС, что противоречит тому, что АВС разносторонний.

Рис.15

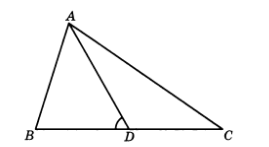
Поэтому разносторонний треугольник разрезать на 2 равных треугольника нельзя.

8.4. Сравните числа: √2011 + √2009 и 2√2010

Решение:

Пусть A = √k + 1 + √k - 1 B = 2√k, (где k = 2010). Тогда A² - B² = 2k + 2√k² - 1 - 4k = 2 (√k² - 1 - k) < 0. Поэтому A < B

8.5. Часы показывают полдень. Через какое время часовая и минутная стрелки снова совпадут?

Решение: Стрелки совпадут снова в 1 ч  мин. Возможный вариант решения может быть такой. До совпадения часовая стрелка опишет угол х градусов, а минутная — (х +360) градусов. Так как минутная стрелка движется в 12 раз быстрее часовой стрелки, то получим уравнение 12x = x + 360, из которого находим . Переведя угол в часы и минуты, получим в 1 ч мин

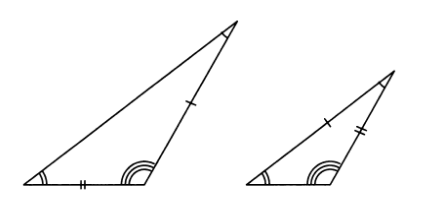
8.6. Равны ли 2 треугольника, если они имеют по 3 равных угла и по 2 равных стороны?

Решение:

Не всегда (рис.16)

Рис.16

8.7. 4 черные коровы и 3 рыжие дают за 5 дней столько молока, сколько 3 черные коровы и 3 рыжих за 4 дня. У каких коров удои больше — у черных или у рыжих?

Решение:

Из условия следует, что 20 черных коров и 15 рыжих дают за 1 день столько же молока, что и 12 черных и 20 рыжих коров. Тогда 8 черных коров дают столько же молока, сколько 5 рыжих. Поэтому у рыжих коров удои больше.

8.8. На какую цифру оканчивается число 2009²⁰¹¹?

Решение: Так как нас интересует последняя цифра результата, то определим последнюю цифру числа 9²⁰¹¹. Число 9 при возведении в степень дает 2 варианта последней цифры — 9 (если показатель степени нечетный) и 1 (если показатель степени четный). Так как 2011 — число нечетное, то 9²⁰¹¹ оканчивается цифрой 9.

8.9. За круглым столом сидят 20 человек, причем более половины юношей. Докажите, что какие-то два юноши сидят напротив друг друга.

Решение:

Объединяя 2 человек, сидящих друг напротив друга в пары, получим 10 пар. Так как юношей больше 10, то в одной из пар будут только юноши.

8.10. В классе 37 учеников. Докажите, что среди них найдутся 4 ученика, отмечающих день рождения в один месяц.

Решение: Если в каждый месяц родилось не более 3 учеников, то всего учеников будет не больше 36. А по условию их 37, значит, такого быть не может. Поэтому найдется 4 ученика, отмечающиеся день рождения в один месяц.

8.11. Три подруги-ученицы: отличница Белова, хорошистка Чернова и троечница Рыжова собирались на дискотеку. Вдруг черноволосая заметила: «Как интересно, одна из нас — имеет белые волосы, другая — черноволосая, а третья — рыжая. Но ни у кого из нас цвет волос не совпадает с фамилией». «Да, ты права», — поддержала отличница. Какого цвета волосы были у хорошистки?

Решение:

Черноволосой не может быть отличница, так как отличница подтвердила слова черноволосой. Поэтому черные волосы у Рыжовой. Тогда Белова будет иметь рыжие волосы, а Чернова — белые.

8.13. Сосчитайте:

Решение: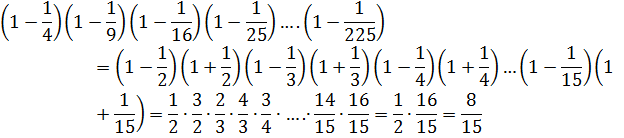

8.14. Как построить угол в 1°, имея шаблон угла величиной в 19°?

Решение: Так как 1 = 19- 19-360, то для построения угла 1° надо 19 раз отложить угол 19° таким образом, чтобы все время одна из сторон у 2 соседних углов была общей. При девятнадцатом откладывании первый и девятнадцатый углы в пересечении дадут 1°.

8.15. Кощей Бессмертный зарыл клад на глубину 1 м. Этого ему показалось недостаточно, он откопал клад, углубил колодец до 2 м и снова зарыл. Этого ему снова показалось мало, он отрыл клад, углубил яму до 3 м и зарыл. Затем он проделал то же, углубив колодец до 4 м, потом до 5 м, до 6 м и т. д. Известно, что колодец глубиной п метров Кощей выкапывает за n² . Известно также, что на 1001-й день Кощей умер от непосильной работы. На какой глубине остался клад? (Временем, необходимым для закапывания колодца, пренебречь.)

Решение:

Через 1² + 2² + 3² + ... + 13² = 819 дней Кощей зарыл клад на глубину 13 м. Зарыть клад на глубину 14 м он не успел, так как 819 + 14² = 1015, а 1015 > 1001.

Но открыть клад и выложить его на землю Кощей успел, так как 819 +13²= 988 и 988 < 1001. Значит, клад будет на глубине 0 м, то есть на земле.

8.16 Докажите, что n² + n + 1 при любом натуральном n:

а) есть число нечетное;

б) не является квадратом никакого другого натурального числа.

Решение а) n² + n + 1 = n (n + 1)². Так как n (n +1) - число четное, то n (n +1) + 1 - будет нечетным числом

б) Ближайшие к числу n² + n + 1 квадраты находятся среди натуральных чисел n² и (n + 1)², но n² + n + 1 < (n + 1)²

Так как n² и (n + 1) — квадраты последовательных натуральных чисел, а число n² + n + 1 находится между указанными квадратами, то оно само не может быть квадратом натурального числа.

8.16. Среди 81 монеты имеется 1 фальшивая (более легкая). Как ее найти, используя всего 4 взвешивания?

Решение:

Разделим монеты на три кучки по 27 монет. Взвесим первую и вторую кучки. Если весы в равновесии, то фальшивая монета в третьей кучке. Если весы не в равновесии, то фальшивая монета в той кучке, которая легче. После этого разбиваем кучку из 27 монет (в которой есть фальшивая монета) на три кучки по 9 монет и вторым взвешиванием определяем более легкую кучку. Третьим взвешиванием определяем наиболее легкую тройку монет. И наконец, четвертым взвешиванием определяем фальшивую искомую монету.

8.17. Пусть а,b — катеты прямоугольного треугольника, а с — гипотенуза. Что больше: a³ + b³ или с³?

Решение:

Равенство a² + b² = c² умножим на с: a²c + b²c. Так как  c > a и c > b, то a²c > a³, b²c > b³. Тогда a²c + b²c > a³ + b³, но a²c + b²c = c³, следовательно a³ + b³ > c³

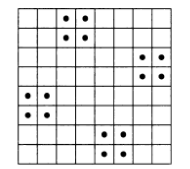
8.18. Можно ли в центры клеток шахматной доски 8x8 вбить 16 гвоздей так, чтобы никакие три гвоздя не лежали на одной прямой?

Решение:

Возможный вариант рис.17

Рис.17

8.20. Бригада лесорубов решила вырубить сосновый лес, но экологи запротестовали. Тогда бригадир успокоил экологов, сказав им: «В нашем лесу сосны составляют 99% от всего леса. После рубки леса сосны будут составлять 98% всех деревьев». Какую часть леса вырубит бригада?

Решение:

При рубке сосен количество деревьев других пород не изменится. Вначале эти деревья составляли 1% леса, а после рубки составят 2% леса. Но если доля прочих деревьев возрастет в 2 раза, то это означает, что лес уменьшится в 2 раза. Поэтому бригада вырубит половину леса.

9 класс

9.1. Решите систему уравнений: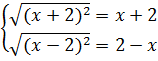

Решение:

Ответ -2 ≤ x ≤ 2

9.2. Найдите сумму коэффициентов многочлена, получающегося после раскрытия скобок и приведения подобных членов в выражении (4 - 5x + x²)²⁰¹⁰ = (4 + 5x + x²)²⁰¹¹.

Решение:

Поскольку = A(1) = (4 - 5 ⋅ 1 + 1²)²⁰¹⁰ (4 + 5 ⋅ 1 + 1²)²⁰¹¹ = 0

9.3. Иван сказал в этом году: «Мне будет n лет, когда пойдет n² год». В каком году родился Иван?

Решение:

Иван родился в 1980 году. Ему будет 45 лет в 2025 году.

9.4. Решите уравнение: x² + xy + y² - 2x + 2y + 4 = 0

Решение:

x² + xy + y² - 2x + 2y + 4 = 0. Умножим обе части уравнения на 2 и сгруппируем (x² + 2xy + y²) + (x² - 4x + 4) + (y² + 4y + 4) = 0.

(x + y)² + (x - 2)² + (y + 2)² = 0, x = 2, y = -2

Ответ: (2;-2)

9.5. Дома Винни-Пуха, Пятачка, Кролика и Совы расположены на окружности. Где нужно построить дом ослику Иа, чтобы сумма расстояний от него до домов остальных была наименьшей?

Решение: В точке пересечения диагоналей четырехугольника, вершинами которого являются домики друзей ослика Иа.

9.6. Цены снизили на 20%. На сколько процентов больше можно купить товаров на те же деньги?

Ответ: на 25%

9.8. Разрежьте квадрат на 5 прямоугольников так, чтобы у соседних прямоугольников стороны не совпадали.

Решение:

Рис.18

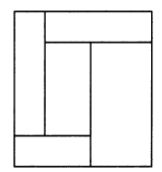
9.9. Известно, что а+b+с=5, ab+bc+ac =5 Чему может равняться a² + b² + c²?

Решение:

Возвести обе части равенства а+b+с=5 в квадрат.

Ответ: 15.

9.10. Четверо ребят — Алексей, Борис, Владимир и Григорий участвовали в лыжных гонках. На следующий день, на вопрос кто какое место занял, они ответили так:

Алексей: «Я не был ни первым и ни последним».

Борис: «Я не был последним».

Владимир: «Я был первым».

Григорий: «Я был последним».

Известно, что три из этих ответов были правдивыми, а один — ложью. Кто сказал правду? Кто был первым?

Решение:

Предположим, что солгал Алексей. Тогда получается, что он был первым или последним. Значит, солгали еще Владимир или Григорий. А это противоречит тому, что солгал всего один из ребят. Пусть солгал Борис. Тогда он был последним. Но Григорий также утверждал, что он был последним. Значит, данного случая также не может быть. Пусть солгал Владимир. Тогда он был не первым. В этом случае все получается и первым тогда будет Борис. Последний случай, когда солгал Григорий, быть не может, так как тогда последним никто из ребят не был.

Ответ: правду сказали Алексей, Борис, Григорий. Первым был Борис.

9.11. В очереди в школьный буфет стоят Вика, Соня, Боря, Денис и Алла. Вика стоит впереди Сони, но после Аллы; Боря и Алла не стоят рядом; Денис не находится рядом ни с Аллой, ни с Викой, ни с Борей. В каком порядке стоят ребята?

Решение:

Из того, что Вика стоит впереди Сони, но после Аллы, порядок девочек следующий: Алла, Вика, Соня. Так как Денис не находится рядом ни с Аллой, ни с Викой, то Алла стоит первой, Вика — второй, а Денис может стоять лишь крайним справа. Но так как Алла и Боря не стоят рядом, а Борис не находится рядом с Денисом, то место Бориса — после Вики. Тогда порядок будет такой: Алла, Вика, Борис, Соня, Денис.

9.12. Верно ли, что ?

Решение:

, а , то

9.13. Сравните числа без помощи калькуляторов, таблиц: √66 и √7 + √30

Решение:

Пусть a= √66, b = √7 + √30.

Тогда a² = 66, b² = 37 + 2√210.

Сравним a² - 37 = 29 и b² - 37 = 2√210.

Снова возведем в квадрат a² - 37 и b² - 37.

Получим 29² = 841, (2√210)² = 840 следовательно √66 > √7 + √30

9.16. Освободитесь от иррациональности в знаменателе

дроби:

Решение: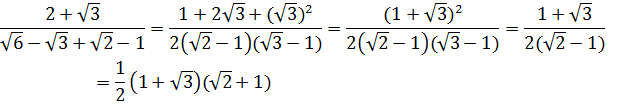

9.17. Найдите двузначное число, равное удвоенному произведению его цифр.

Решение:

Пусть двузначное число имеет вид 10y + x. Так как 10y + x = 2xy — четное число, то и x — цифра четная. Разделив обе части уравнения 10y + x = 2xy на 2y, получим откуда х>5. Учитывая, что x — четная цифра, получим х = 6 или x = 8. Если х = 8, то  и  что невозможно.

Если же x = 6, то у = 3. Тогда искомое число будет 36.

9.18. Докажите, что число ababab делится на 21.

Решение:

ababab = 100000a + 10000b + 1000a + 100b + 10a + b = 101010a + 10101b = 10101 (10a + b). Поскольку 10101 делится на 21, то и ababab делится на 21

9.19. Две стороны треугольника равны 49 см и 99 см, а угол между ними 59°. Каким является этот треугольник: остроугольным, прямоугольным или тупоугольным?

Решение: Пусть АС = 49 см, АВ = 99 см, /ВАС = 59° (см. рис. 19).

Рис.19

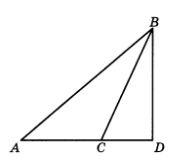
Опустим из вершины В высоту BD на сторону АС. Тогда AD = АВ cos(ВАС )= 99 см cos 59°. Так как косинус убывает на отрезке [0; ], то cos 59° > cos 60° = . Таким образом, AD > 49,5 > АС и, поэтому основание высоты будет на продолжении стороны АС, значит, АВС — тупоугольный.

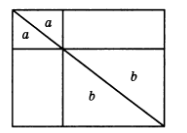
9.20. На диагонали прямоугольника выбрали точку и провели через нее прямые, параллельные сторонам. По разные стороны от диагонали образовались два прямоугольника. Докажите, что их площади равны.

Решение:

Диагональ делит исходный прямоугольник и два внутренних прямоугольника на равные треугольники (рис. 20). Отнимая от равных треугольников равные, получим фигуры равной площади.

Рис.20

10 класс

10.1. Из двух равных трапеций сложите параллелограмм. Как применить данный результат к выводу формулы площади трапеции?

Решение:

На рис. 21 показано, как нужно сложить трапеции.

Рис.21

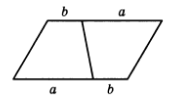
S_пар = (a + b)h, значит, .

10.2. Упростите: .

Решение

=

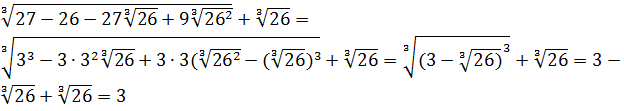
10.3. Прямая, параллельная основанию треугольника, делит его площадь пополам. В каком отношении она делит боковые стороны треугольника?

Решение:

Пусть (рис 21)

Рис.22

Ответ: (√2 - 1) : 1

10.4. Сколько диагоналей в правильном 37-угольнике?

Решение:

10.5. Каждая сторона одного треугольника больше каждой стороны другого треугольника. Верно ли, что площадь первого обязательно больше площади второго?

Решение:

Нет, пример приведен на рис. 23 (площадь △ABC меньше площади △MNK).

Рис.23

10.6. В уравнении (x2 + ...)(x + 1) = (x⁴ + 1)(x + 2) одно число стерто и заменено точками. Найдите стертое число, если известно, что один из корней этого уравнения равен 1.

Решение:

Заменим х на 1. Получим, что стертое число равно 2

10.7. Хулиган Витя вырезал из школьной стенгазеты в форме квадрата все то, что ему не понравилось. В итоге остался кусок в форме правильного восьмиугольника. Можно ли по этому восьмиугольнику узнать размеры школьной стенгазеты, если отрезанных кусков было 5, и они имели форму многоугольника?

Решение:

Так как оставшийся кусок имеет форму правильного восьмиугольника, а отрезанных кусков — пять, то они могут иметь не больше одной общей стороны со стороной восьмиугольника. Значит, минимум три стороны восьмиугольника принадлежат квадрату. Поэтому форма искомой стенгазеты будет квадрат со стороной, равной расстоянию между противоположными сторонами восьмиугольника. Вырезанные же многоугольники будут: пять треугольников или четыре треугольника и один четырехугольник, причем два треугольника (один треугольник и четырехугольник) будут в сумме составлять один из оставшихся трех треугольников.

10.8. Найдите четырехзначное простое число, цифры которого образуют арифметическую прогрессию.

Решение:

Разность прогрессии может быть равной лишь 1,-1, 2,-2. Так как четной цифрой число заканчиваться не может, то начинаться оно должно с четной цифры (при разности 1 или -1) или нечетной цифры (при разности 2 или -2). Рассматривая возможные варианты: 2345, 4567, 6789, 8765, 6543, 4321, 1357, 3579, 9753, 7531 — находим единственное простое число: 4567.

10.9. От 2 кусков сплавов с разным содержанием свинца массой 6 кг и 12 кг отрезали по куску равной массы. Каждый из отрезанных кусков сплавили с остатком другого сплава, после чего процентное содержание свинца в обоих сплавах стало одинаковым. Каковы массы отрезанных кусков?

Решение:

Пусть в первом куске процентное содержание свинца будет а%, а во втором — b%. Пусть от первого и второго кусков отрезали по х кг. Тогда получим процентное содержание свинца в первом сплаве:

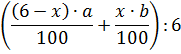
а во втором:

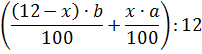
Так как они равны, то получим уравнение:

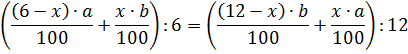
Произведя упрощения, получим: 3x (a - b) = 12 (a - b). Так как (a - b) ≠ 0, то х=4 (кг). Массы отрезанных кусков равны 4 кг.

Ответ: 4 кг.

10.10. Дан круг. Постройте круг, площадь которого была бы больше площади данного круга в 10 раз.

Решение:

Обозначим радиус данного круга за r. Тогда радиус искомого круга R = √10r = √r² + 9r². Его можно найти как длину гипотенузы прямоугольного треугольника с катетами r и 3r.

10.11. Можно ли расположить по кругу цифры 1,2,3,..., 9 так, чтобы сумма никаких 2 соседних чисел не делилась ни на 3, ни на 5, ни на 7?

Решение:

Можно. Начнем с 1. Соседними с ней могут быть только 3 и 7. Соседним с 7 могут быть 4 или 6 или 9.

Выберем 4, тогда вторым соседним числом с 4 может быть только 9. Рассуждая далее аналогично, получим такое расположение чисел: 3-1-7-4-9-2-6-5-8-3.

10.12. В магазине продается краска, расфасованная в банки по 3 кг и 5 кг. Докажите, что в этом магазине покупатель всегда может купить нужное, больше 7, число килограммов краски.

Решение:

Обозначим число килограммов краски, которое надо купить, за N. Тогда N будет иметь вид 3n, Зn + 1, или Зn + 2.

Рассмотрим числа вида Зn. Тогда надо брать число банок n, все массой по 3 кг.

Рассмотрим числа вида Зn + 1. Минимальное число килограммов краски этого вида будет 10 кг. Тогда 10 = 5+5. Если Зn + 1 > 10, то берем 2 банки краски по 5 кг и (n-3) банки краски по 3 кг (З(n-З) + 10 = Зn + 1).

Рассмотрим числа вида Зn + 2. Тогда минимальное число такого вида, большее 7, будет 8 = 3+5. Если же Зn + 2 > 8, то берем 1 банку по 5 кг и n-l банку по 3 кг (3(n-1) + 5 = 3n-3 + 5 = 3n + 2).

10.13. По горизонтальной дороге мотоциклист ехал со скоростью 60 км/ч. На пути ему встретился подъем протяженностью 2 км, за которым следовал спуск протяженностью также 2 км. На подъеме мотоциклист ехал со скоростью 30 км/ч. С какой скоростью мотоциклист должен ехать на спуске, чтобы средняя скорость на подъеме и на спуске составляла 60 км/ч?

Решение: Достичь требуемого невозможно. Следуя со скоростью 60 км/ч, мотоциклист проезжает за минуту 1 км, а за 4 мин — 4 км. При скорости 30 км/ч он проезжает подъем протяженностью 2 км за 4 мин. Поэтому на спуск ему времени не остается.