1Ықтималдық теориясының элементтері_дидактикалық материал

1-топ.

Екі тиынды лақтырғанда олардың жақтарының түсуінің барлық мүмкін жағдайларын әртүрлі тәсілдермен көрсетіңіз.

а) қысқаша жазып шығу арқылы: ЕЕ, ЕС, СЕ, СС.

б) екі өлшемді жазықтықты қолдану арқылы:

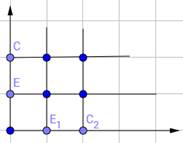
в) талдау ағашы арқылы

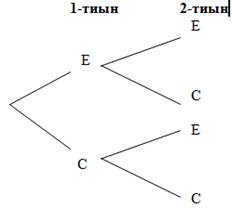
Енді оқушылар осы тапсырма бойынша ықтималдықты таба алады, мысалы: екі тиынның да елтаңба жағының түсу ықтималдығы  екені анық көрінеді немесе екеуінің біреуінде елтаңба жағының түсуі  екені белгілі болады, өйткені барлық жағдайлар саны 4, ал қолайлы жағдайлар саны 2.

2-топ.

Ойын сүйегінің жақтарында 0, 0, 1, 1, 4 және 5 сандары белгіленген. Егер ойын сүйегі екі рет тасталған болса, онда

а) түскен жақтарының қосындысы 5 болу ықтималдығын табыңыз;

ә) екі рет те бірдей сандар түсу ықтималдығын табыңыз. 

Екі өлшемді жазықтықты қолдану арқылы табуға болатынын көрсетіңіз:

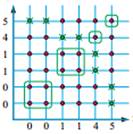
Жауабы: а)  ; ә)

3-топ.

1-тоқсанда өткен «Жиындар теориясы» тақырыбын еске түсіріп, сол арқылы оқиғаның ықтималдығын табайық:

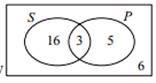
Сыныпта 30 оқушы бар. Оның 19-ы спортпен шұғылданады, 8-і пианинода ойнайды, 3 оқушы спортпен де шұғылданады және пианино ойнайды. Осы ақпаратты Эйлер-Венн диаграммасында бейнелеп, кездейсоқ алынған оқушының:

а) спортпен шұғылдану және пианинода ойнау ықтималдығын табыңыз;

ә) спортпен шұғылдану немесе пианинода ойнау ықтималдығын табыңыз;

б) спортпен шұғылданып, бірақ пианинода ойнамау ықтималдығын табыңыз;

в) тек бір ғана спортпен шұғылдану немесе пианинода ойнау ықтималдығын табыңыз;

г) спортпен де шұғылданбау, пианинода да ойнамау ықтималдығын табыңыз;

ғ) пианинода ойнайтын, егер ол оқушы спортпен шұғылданатыны белгілі болса.

Жауабы: а) ; ә) ; б) ; в) ; г) ; ғ)  (егер оқушының спортпен шұғылданатынын білетін болсақ, онда сол оқушылардың ішінен ғана пианинода ойнайтын оқушыларды қарастырамыз).

Тапсырма:

   1) Телефон номерін теріп жатқанда абонент бір цифра ұмытып қалады, және оны кездейсоқ тереді. Керек цифраны тергенінің ықтималдығын тап

Жауабы: .

  2) Жәшікте  15 бұйымдар бар, оның 10 боялған. Жинақтаушы кездейсоқ 3-ін алады. Алынған  бұйымдар боялған болатынының ықтималдығын табыңыз.

Жауабы: .

3) Жәшікте  100 бұйымдар бар, оның 10 жарамсыз. Кездейсоқ 4 бұйым алынған. Алынған бұйымдардың ішінде: а) жарамсыз жоқ; б) пайдалысы жоқ екенінің ықтималдығын табыңыз.

Жауабы: а) ≈0,65

б) ≈0,00005.

 4) Ойын “сүйегі” (кубигі) лақтырылды. Жұп ұпай саны түсетінінің ықтималдығы қандай.

Жауабы: 0,5.

5) Жәшіктен 1-ден бастап 100-ге дейін нөмерленген жетондар суырылған. Бірінші алынған жетонның нөмірінің ішінде 5 цифрасы болмайтындығының ықтималдығын тап:

Жауабы: 0,81.

6) Қаптың ішінде 5 бірдей кубиктер бар. Әр кубиктің барлық жағында мына әріптердің біреуі жазылған:  о, п, р, с, т. Бір сызық бойында жатқан және бір-бірден алынған кубиктерден  «спорт» сөзін оқып шығуға болатындығының ықтималдығын тап.

Жауабы: .

7) Барлық жақтары боялған куб, бірдей өлшемді 1000 кубиктерге бөлінген, олар содан соң араластырылған. Кездейсоқ алынған кубиктің боялған жақтары а) бір; б) екі; в) үш болатынының ықтималдығын табыңыз. Жауабы: а) 0,384; б) 0,096; в) 0,008.

8) 100 бөлшегі бар ұйымнан техникалық бақылау бөлімі 5стандартты емес бөлшек тапқан. Стандартты емес бөлшектердің шығуының салыстырмалы ықтималдығын тап

Жауабы: 0,05.

9) Жазықтықта радиустары сәйкесінше 5 және 10 см-ге тең екі шеңбер сызылған. Кездейсоқ үлкен доңгелекке лақтырылған нүкте шеңберлер арасындағы сақинаның ішіне түсетінің ықтималдығын табыңыз. Нүктенің жазық фигураның ішіне түсетінінің ықтималдығы фигураның ауданына пропорционал және оның орналасуына тәуелді емес.

Жауабы: 0,75.

10) Радиусы R-ға тең дөңгелек ішіне нүкте лақтырылған. Дөңгелекке іштей сызылған: а)  шаршының; б) дұрыс үшбұрыштың в)  дұрыс алтыбұрыштың ішінде нүкте болатынының ықтималдығын тап. Нүктенің дөңгелек бөлігінің ішіне түсу ықтималдығы  осы бөліктің ауданына пропорционал және оның дөңгелек арқылы орналасуына тәуелді емес.