2x2 біматрічні ігри. Ситуація рівноваги

2x2 біматрічні ігри. Ситуація рівноваги

Ми припускаємо приділити основну увагу злучаю, коли у кожного з гравців є рівно дві стратегії, тобто злучаю т = п = 2. Тому нам здаеться доречним виписати приведені вище формули саме для такого випадку. У 2 ´ 2 біматрічній грі платіжні матриці гравців мають наступний вигляд

1)     

2)                    ,     ,

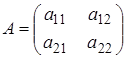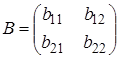ввірогідності

а середнє виграшу знаходять за формулами

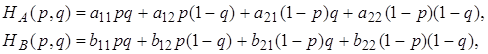
де

,

1.      

2.     Сформулюємо визначення

Визначення. Будемо вважати, що пара чисел

,     ,    

визначає рівнозважену ситуацію, якщо для р и q, підлеглих умовам   одночасно виконується наступні нерівності

                                                                                       (1)

Пояснення. Виписані нерівності (1) означають наступне: ситуація, визначаємо змішаною стратегією (р*, q*), є рівноважною, якщо відхилення від неї одного з гравців за умови, що інший зберігає свій вибір, призводить до того, що виграш гравця, що відхилився, може тільки зменшитися. Тим самим, виходить, що якщо рівноважна ситуація існує, то відхилення від неї невигідно самому гравцеві.

Теорема 1 (Дж. Неш). Всяка біматрічна гра має хоч би одну рівноважну ситуацію (точку рівноваги) в змішаних стратегіях.

Отже, рівноважна ситуація існує. Але як її знайти?

Якщо деяка пара чисел (р*, q*) претендує на те, щоб визначати ситуацію рівноваги, то для того, щоб переконатися в обґрунтованості цих претензій, або, навпаки, довести їх необґрунтованість, необхідно перевірити справедливість нерівностей (1) для будь-якого р в межах від 0 до 1 і для будь-якого q в межах від 0 до 1. У загальному випадку число таких перевірок нескінченне. І, отже, діючий спосіб визначення рівноважної ситуації потрібно шукати десь в іншому місці.

Теорема 2. виконати нерівність

                                                                                           (1)

Рівносильне виконанню нерівностей

                                                    (2)

Іншими словами, для того, щоб переконатися в обґрунтованості претензій пари (р*, q*) на те, щоб визначати рівноважну ситуацію, потрібно перевірити справедливість нерівності

тільки для двох чистих стратегій гравця А (р = 0 і р = 1) і нерівності

тільки для двох чистих стратегій гравця В (q = 0 і q= 1).

Чотири нерівності (2) дозволяють провести пошук точки рівноваги цілком конструктивно. Запишемо середні виграші гравців А і У в зручнішій формі.

Маємо

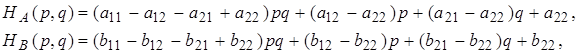
Звернемося до першої з отриманих формул.

Вважаючи в ній спочатку р = 1, а потім р = 0, отримуємо

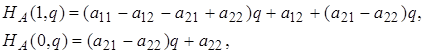
Розглянемо різниці

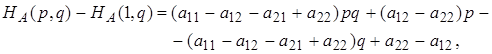
Вважаючи

отримаємо для них наступні вирази

только для двух чистых стратегий игрока В (q = 0 и q= 1).

Чотири нерівності (2) дозволяють привести точки рівноваги цілком конструктивно.

Запишемо середні виграші гравців А і В в більш зручній формі. Маємо:

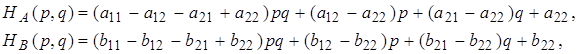
У випадку, якщо пара  (р, q)  визначає точку рівноваги, ці різності негативні отрицательній

Тому отримуємо

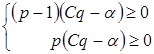
З формул для функцій маємо н_в ( р, q) при q = 1 и q = 0 відповідно маємо

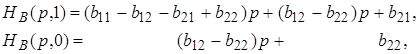
Різності

 и

З урахуванням позначень

 .

Приводяться до виду

абсолютно так само, як відповідні різниці для функції Н_А.

Якщо пара (р, q)  визначає точку рівноваги, то ці різності не негативні

тому

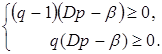
Висновки

Для того , щоб у біматричній грі

,     ,

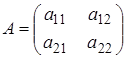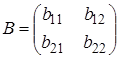пара (р, q)  визначала рівноважну ситуацію, необхідно й досить одночасне виконання  наступних нерівностей

,    ,

,    ,

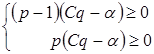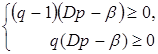де

    .