«Диофантовы уравнения»
Содержание:
1. Введение
2. Диофант Александрийский
3. Уравнение
4. Диофантовы уравнения
5. Заключение
6. Список используемых источников
Введение
Станет ли кто в наше время отрицать настоятельную необходимость самого широкого распространения и популяризации математических знаний? Первоначальные математические познания должны входить с самых ранних лет в наше образование и воспитание.
Алгебра – один из больших разделов математики. Она возникла как наука об уравнениях в связи с потребностями практики, в результате поиска общих приемов однотипных задач. Само слово «алгебра» (аль – джебр) является начальным словом в названии одного из сочинений известного узбекского математика 9 века Мухаммеда аль Хорезми (аль – джебр означает один из приемов преобразования уравнений).
Уравнение одно из важнейших понятий математики. В большинстве практических и научных задач, где какую – то величину нельзя непосредственно измерить или вычислить по готовой формуле, удается найти эту величину благодаря уравнениям.
Диофантовы уравнения – это уравнения в целых числах. В качестве примера может послужить задача о размере рубля монетами разных достоинств. Решение уравнений в целых числах – очень увлекательная задача.
Это один из самых красивых разделов математики. Ни один крупный математик не прошел мимо теории диофантовых уравнений.
Диофант Александрийский
 Диофант
Александрийский — древнегреческий математик, живший
предположительно в III веке н. э. О подробностях его жизни практически
ничего не известно. С одной стороны, Диофант цитирует Гипсикла (II век
до н. э.); с другой стороны, о Диофанте пишет Теон
Александрийский (около 350 года н. э.), — откуда можно сделать
вывод, что его жизнь протекала в границах этого периода. Возможное уточнение
времени жизни Диофанта основано на том, что его Арифметика посвящена
«достопочтеннейшему Дионисию». Полагают, что этот Дионисий — не кто иной,
как епископ Дионисий Александрийский, живший в середине III в.
н. э.
Диофант
Александрийский — древнегреческий математик, живший
предположительно в III веке н. э. О подробностях его жизни практически
ничего не известно. С одной стороны, Диофант цитирует Гипсикла (II век
до н. э.); с другой стороны, о Диофанте пишет Теон
Александрийский (около 350 года н. э.), — откуда можно сделать
вывод, что его жизнь протекала в границах этого периода. Возможное уточнение
времени жизни Диофанта основано на том, что его Арифметика посвящена
«достопочтеннейшему Дионисию». Полагают, что этот Дионисий — не кто иной,
как епископ Дионисий Александрийский, живший в середине III в.
н. э.
Его «Арифметика» стала поворотным пунктом в развитии алгебры и теории чисел. Именно здесь произошёл окончательный отказ от геометрической алгебры. В начале своего труда Диофант поместил краткое введение, ставшее первым изложением основ алгебры. В нём строится поле рациональных чисел и вводится буквенная символика. Там же формулируются правила действий с многочленами и уравнениями. Труды Диофанта имели фундаментальное значение для развития алгебры и теории чисел. С именем этого учёного связано появление и развитие алгебраической геометрии, проблемами которой впоследствии занимались Леонард Эйлер, Карл Якоби и другие авторы.
Уравнение.
Уравнением называется равенство, содержащее одну или несколько букв, под которым подразумевается неизвестные числа. Уравнение имеет вид.
![]()
или, в приведённой форме
![]()
где ![]() и
и ![]() — функции (в общем случае — векторные)
одного или нескольких аргументов.
— функции (в общем случае — векторные)
одного или нескольких аргументов.
Решение уравнения — задача по нахождению таких значений аргументов, при которых это равенство достигается. На возможные значения аргументов могут быть наложены дополнительные условия. Аргументы заданных функций (иногда называются «переменными») в случае уравнения называются «неизвестными». Значения неизвестных, при которых это равенство достигается, называются решениями или корнями данного уравнения. Про корни говорят, что они удовлетворяют данному уравнению. Решить уравнение означает найти множество всех его решений (корней) или доказать, что корней нет.
Различают алгебраические, параметрические, трансцендентные, функциональные, дифференциальные и другие виды уравнений.
Некоторые классы уравнений имеют аналитические решения, которые удобны тем, что не только дают точное значение корня, а позволяют записать решение в виде формулы, в которую могут входить параметры. Аналитические выражения позволяют не только вычислить корни, а провести анализ их существования и их количества в зависимости от значений параметров, что часто бывает даже важнее для практического применения, чем конкретные значения корней.
К уравнениям, для которых известны аналитические решения, относятся алгебраические уравнения, не выше четвёртой степени: линейное уравнение, квадратное уравнение, кубическое уравнение и уравнение четвёртой степени. Алгебраические уравнения высших степеней в общем случае аналитического решения не имеют, хотя некоторые из них можно свести к уравнениям низших степеней.
Уравнение, в которые входят трансцендентные функции, называются трансцендентными. Среди них аналитические решения известны для некоторых тригонометрических уравнений, поскольку нули тригонометрических функций хорошо известны.
В общем случае, когда аналитического решения найти не удается, применяют численные методы. Численные методы не дают точного решения, а только позволяют сузить интервал, в котором лежит корень, до определенного заранее заданного значения.
С алгебраическими выражениями, входящими в уравнения, можно выполнять операции, которые не меняют его корней, в частности:
· В любой части уравнения можно раскрыть скобки.
· В любой части уравнения можно привести подобные слагаемые.
· Любой член уравнения можно перенести из одной части в другую, заменив его знак на противоположный.
· К обеим частям уравнения можно прибавить одно и то же выражение.
· Из обеих частей уравнения можно вычесть одно и то же выражение.
· Обе части уравнения можно умножать или делить на одно и то же число, отличное от нуля.
Уравнения, которые являются результатом этих операций, являются эквивалентными начальному уравнению. Однако для свойств 4 и 5 существует ограничение: в случае прибавления к обеим частям уравнения одного и того же выражения (или в случае вычитания из обеих частей уравнения одного и того же выражения), содержащего неизвестное и теряющего смысл при неизвестном, принимающим значения корней данного уравнения, получится уравнение, неэквивалентное исходному (начальному). Но если к обеим частям уравнения прибавить одно и то же выражение (или из обеих частей уравнения вычесть одно и то же выражение), содержащее неизвестное и теряющее смысл лишь при значениях неизвестного, не являющихся корнями данного уравнения, то получится уравнение, эквивалентное начальному.
Умножение или деление обеих частей уравнения на выражение, содержащее неизвестное, может привести, соответственно, к появлению посторонних корней или к потере корней.
Возведение обеих частей уравнения в квадрат может привести к появлению посторонних корней.
Диофантовы уравнения
Диофантовыми уравнениями называются алгебраические уравнения или системы алгебраических уравнений с целыми коэффициентами, для которых надо найти целые или рациональные решения. При этом число неизвестных в уравнениях должно быть не менее двух. Диофантовы уравнения имею, как правило, много решений, поэтому их называют неопределенными уравнениями. К диофантовым уравнениям приводят задач, по смыслу которых неизвестные значения величин могут быть только целыми числами. В качестве примера задача на составления диофантовых уравнений, может служить задача о размере рубля монетами достоинством в 1; 2; 3; 5; 10; 15 и 50 копеек. Соответствующее уравнение имеет вид:
50 Х8 + 20Х7 + 15Х6 + 10Х5 + 5Х4 + 3Х3 + 2Х2 + 1Х1 = 100
Решить такое уравнение – это значит найти все такие наборы.
Х8 Х7 Х6 Х5 Х4 Х3 Х2 Х1 удовлетворяющие 50 Х8 + 20Х7 + 15Х6 + 10Х5 + 5Х4 + 3Х3 + 2Х2 + 1Х1 = 100.
Число наборов, удовлетворяющих этому уравнению примерно равно
510 * 107. Названы эти уравнения по имени греческого математика. Его книга «Арифметика» содержала большое количество интересных задач, его изучали математики всех поколений. Книга сохранилась до наших дней, её можно найти в русском переводе в библиотеке. К диофантовым уравнениям приводят задачи, по смыслу которых неизвестные значения величин могут быть только целыми числами.
Для линейных уравнений с двумя неизвестными, т.е. уравнение вида
ax + by = c, где a, b, c – целые числа, а x, y – целочисленные решения уравнения. для данного уравнения справедливы следующие утверждения:
1) Если коэффициенты a и b уравнения ax + by = c являются взаимно простыми числами (их наибольший общий делитель d=1), то это уравнение имеет, по крайней мере, одно целочисленное решение.
2) Если d≠1, то уравнение ax + by = c не имеет целочисленных решений.
3) Если d=1/ то уравнение ax + by = c имеет бесконечное множество целочисленных решений, которые задаются формулами
х = α + bt, y = β – at,
Где (α ; β ) – некоторое целочисленное решении уравнения ax + by = c , at t – произвольное целое число.
Долгое время надеялись отыскать общий решения любого диофантова уравнения. Однако в 1970 году ленинградский математик Ю.В. Матиясевич доказал, что такого общего способа быть не может.
Рассмотрим решение системы диофантовых уравнений первой степени на конкретном примере:
Решить в целых числах систему уравнений:
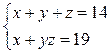
Решение: вычтем из второго уравнения первое, получим yz-y-z=5
или (y-1)(z-1)=6. Число 6 можно разложить на целые множители четырьмя способами:
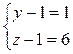
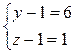
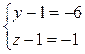
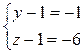
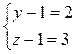
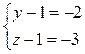
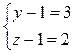
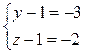
Эти системы дают тройки значений
(x;y;z): (5;2;7), (5;7;2), (7;4;3), (7;3;4), (19;-5;0), (17;-2;-1), (17; -1;-2).
Диофантовы уравнения решаются методом перебора (один из самых древнейших методов решения математических задач возникающих на практике).
А так же нужно помнить, что если число d есть наибольший делитель целых чисел a и b, то существует такие числа k и 1, что d=ka + lb. Алгоритм Евклида позволяет вычислить целые числа k и 1.
Линейное диофантово уравнение ax + by = c не будет иметь решений, если числа с и d взаимно простые. Если число с кратно числу d, то одно из решений уравнения будет иметь вид: x=pk и y=pl.
Если целое число c делится на D(a;b), то уравнение ax + by = c имеет целые решения (если некоторые из чисел a, b и с отрицательны, то вместо них берем их модули).
Рассмотрим, как искать эти решения на следующем примере:
Найти целые решения уравнения: 28x – 40y=60
Это уравнение может иметь целые решения, так как D(28;40)=4, а число 60 делится на цело, на 4. Ясно, что любое целое решение уравнения
28x – 40y=60 удовлетворяют и уравнению 7x – 10y = 15 из заданного сокращения обеих частей на 4. Обратно любое целое решение уравнения
7x – 10y = 15, является и целым решением заданного уравнения.
У получившегося после сокращения на 4 уравнение 7x – 10y = 15 коэффициенты при неизвестных взаимно просты, т.е. D(7;10) равно 1.
Применим к этим коэффициентам алгоритм Евклида. Мы видим, что при делении числа 7 на 3 получилось неполное частное 2 и остаток 1, а потому 7 = 2*3 + 1. Значит 1=7-2*3. таким же путем устанавливаем, что 10=1*7+3, а потому 3=10-1*7. Подставляя это выражение в равенство 1=7-2*3, получаем 1=7-2(10-1*7).
Раскрывая скобки, получаем x=3 и y=2 дают целые решения уравнения
7x – 10y = 15. Чтобы получить целые решения уравнения 7x – 10y = 15, надо оба этих числа умножить на 15. Таким путем мы получим одно решение уравнения 7x – 10y = 15: х=45, y=30. Другие целые решения того же уравнения имеют вид: х=45+10t, y=30 + 7t, где t – любое число.
Чтобы выделить целые неотрицательные решения заданного уравнения, надо найти такие значения t, при которых 45 +10t>0 и 30+7t>0. Из этих неравенств находим, что должны выполняться условия t>-4,5, t>-30/7, из которых вытекает, что t>-4.
Итак, данное уравнение имеет бесконечно много целых неотрицательных решений, задаваемых формулами х=45+10t, y=30 + 7t, где t принимает значение -4, -3,-2, …
Заключение
Решение уравнений в целых числах – один из самых красивых разделов математики. Ни один крупный математик не прошел мимо теории диофантовых уравнений. Ферма, Эйлер, Лагранж, Дирихле и Гаусс, Чебышев и Риман оставили неизгладимый след в этой интереснейшей теории.
Список используемых источников
1.Абрамов А.М., Абрамов В.М., «Математика от А до Я» - Москва, 2002.
2.Колягин Ю.М. «Алгебра и начала математического анализа 10 класс» - Просвещение, 2010.
3. Калкин Р.А. «Алгебра и элементарные функции» - Москва, 1975.
4. Касаткин В.Н. «Математика» - Москва,1989.
5. Петраков И.Н. «справочник по математике» - Москва, 1981.
6. http://ru.wikipedia.org
Скачано с www.znanio.ru
© ООО «Знанио»
С вами с 2009 года.
![]()


