
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
Цикловая комиссия физико-математических дисциплин
Уколова Ю.В.
ФИЗИКА
ПРАКТИКУМ
для курсантов специальности
26.02.05 Эксплуатация судовых энергетических установок
профиля: технического
очной форм обучения
Керчь, 2016 г.

СОДЕРЖАНИЕ
ВВЕДЕНИЕ 4
Практическое занятие №1. Тема: Кинематика и динамика поступательного 6
движения твердого тела.
Практическое занятие №2. Тема: Кинематика и динамика вращательного 20
движения твердого тела. Законы сохранения
Практическое занятие №3. Тема: Молекулярно – кинетическая теория 37
идеальных газов.
47
Практическое занятие №4. Тема: Основы термодинамики
Практическое занятие №5. Тема: Электростатика. Постоянный 60
электрический ток
Практическое занятие №6. Тема: Магнитное поле. Электромагнитная 83
индукция.
98
CПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
99
Приложение А. Таблица вариантов индивидуальных работ
103
Приложение Б. Справочные материалы. Табличные данные.
Знание законов физики предполагает умение не только формулировать эти законы, но и применять их при решении конкретных практических задач. Умение решать задачи способствует приобщению студентов к самостоятельной творческой работе, учит анализировать изучаемые явления, выделять главные факторы, их обусловившие. Наибольшую пользу приносит процесс решения задач при условии самостоятельности этого процесса, которую и призвано обеспечить данное методическое руководство
В этой связи, главная цель, поставленная в данном пособии, состоит в том, чтобы как можно полнее показать пути использования и способы применения на практике теоретического материала по дисциплине «Физика», изучаемого на лекциях. Изложенный материал нацелен на решение следующих дидактических задач:
– глубокое усвоение и закрепление в памяти студентов (курсантов) основных теоретических положений и законов по указанному разделу физики;
– формирование практических умений и навыков применения теории в процессе решения задач;
– знакомство с различными математическими приемами и способами получения решения физической задачи в общем виде;
Предлагаемое пособие содержит материал к практическим занятиям по физике, включающий:
1)предлагаемые студентам для теоретической подготовки к занятиям вопросы;
2)подробные методические указания по решению широкого спектра задач;
3)задачи для самостоятельного индивидуального решения;
3)в конце пособия имеются приложения, содержащие дополнительный материал, справочные таблицы.
Согласно рабочей программе, на практические занятия отводится 12аудиторных часа.
Сознательное решение задач возможно при условии усвоения соответствующего теоретического материала. Для этого по каждой теме приводятся контрольные вопросы, позволяющие заострить внимание студентов при подготовке к занятиям на краеугольные проблемы темы или раздела и глубже разобрать их.
Пользуясь данным пособием, студент должен:
Ø целенаправленно, по контрольным вопросам и указанной литературе, изучить предлагаемый раздел;
Ø самостоятельно, опираясь на изученную теорию, методические указания и примеры, выполнить домашнее задание в соответствии с указанным преподавателем вариантом.
При решении задач целесообразно руководствоваться следующими правилами:
1.Прежде всего, внимательно прочесть условие, вникнуть в него. Если характер задачи позволяет, обязательно сделать пояснительный рисунок.
2.Произвести анализ задачи, выяснить, о каких объектах или процессах идет речь, какие величины его определяют, каким физическим закономерностям подчиняются рассматриваемые явления.
3.Выбрать оптимальный метод решения задачи.
4.Решение задачи проводить сначала в общем виде, при этом искомая величина должна быть выражена через заданные в условии величины.
5.Подстановка числовых данных должна производиться в одной системе единиц – системе СИ.
![]()
![]() 6.При
подстановке в расчетную формулу, а также при записи ответа числовые значения
физических величин следует записывать как десятичной дроби с одной значащей
цифрой пред запятой на соответствующую степень десяти. Например, вместо 5460
надо записать 5,46 103
, вместо 0,00263 записать 2,63
10 3 и т.п. Вычисления по расчетной формуле следует проводить
с соблюдением правил приближенных вычислений. Как правило, окончательный ответ
следует записывать с точностью до 0,01.
6.При
подстановке в расчетную формулу, а также при записи ответа числовые значения
физических величин следует записывать как десятичной дроби с одной значащей
цифрой пред запятой на соответствующую степень десяти. Например, вместо 5460
надо записать 5,46 103
, вместо 0,00263 записать 2,63
10 3 и т.п. Вычисления по расчетной формуле следует проводить
с соблюдением правил приближенных вычислений. Как правило, окончательный ответ
следует записывать с точностью до 0,01.
7.В конце решения производиться проверка соответствия единиц измерения.
8.При оформлении домашнего задания используемые законы и формулы должны быть кратко, но исчерпывающе пояснены.
9.Если представляется возможным, оценить правдоподобность полученного численного ответа.
Критерии оценивания индивидуальных практических заданий.
Оценка «5» ставится за работу, выполненную полностью без ошибок и недочётов.
Оценка «4» ставится за работу, выполненную полностью, но при наличии в ней не более одной негрубой ошибки и одного недочёта, не более трёх недочётов.
Оценка «3» ставится, если студент (курсант) правильно выполнил не менее 2/3 всей работы или допустил не более одной грубой ошибки и двух недочётов, не более одной грубой и одной негрубой ошибки, не более трёх негрубых ошибок, одной негрубой ошибки и трёх недочётов, при наличии четырёх-пяти недочётов.
Оценка «2» ставится, если число ошибок и недочётов превысило норму для оценки «3» или правильно выполнено менее 2/3 всей работы.
1. Незнание определений основных понятий, законов, правил, основных положений теории, формул, общепринятых символов обозначения физических величин, единиц измерения.
2. Неумение выделить в ответе главное.
3. Неумение применять знания для решения задач и объяснения физических явлений.
4. Неумение читать и строить графики и принципиальные схемы.
1. Неточности формулировок, определений, понятий, законов, теорий, вызванные неполнотой охвата основных признаков определяемого понятия, ошибки, вызванные несоблюдением условий проведения опыта или измерений.
2. Ошибки в условных обозначениях на принципиальных схемах, неточности чертежей, графиков, схем.
3. Пропуск или неточное написание наименований единиц физических величин.
4. Нерациональный выбор хода решения.
1. Нерациональные записи при вычислениях, нерациональные приёмы в вычислении, преобразовании и решении задач.
2. Арифметические ошибки в вычислениях, если эти ошибки грубо не искажают реальность полученного результата.
3. Отдельные погрешности в формулировке вопроса или ответа.
4. Небрежное выполнение записей, чертежей, схем, графиков.
5. Орфографические и пунктуационные ошибки.
Тема: Кинематика и динамика поступательного движения твердого тела.
Цель: обобщение и систематизация знаний, умений по данной теме; формирование практических навыков при решении задач; развитие познавательных возможностей, памяти, трудолюбия.
Краткие теоретические сведения
Таблица 1.1 - Основные законы и формулы
|
Физические законы, переменные |
Формулы |
|
Мгновенная скорость: r r dr
производная радиус – вектора материальной точки. |
r
dt |
|
Модуль вектора скорости: где S – путь |
dt |
|
Модуль средней скорости: |
|
|
Мгновенное
ускорение: |
r a
|
|
Модуль вектора ускорения при прямолинейном движении: |
a
|
|
Скорость и путь при движении: 1) равномерном,2) равнопеременном, υ0 – начальная скорость, а>0 при равноускоренном движении, а<0 при равнозамедленном движении. |
2)
|
|
Основное уравнение динамики поступательного движения (II закон
где
F -
результирующая сила. |
rr
|
|
Силы в природе: 1) сила притяжения, закон всемирного тяготения, где G = 6,67·10-11Н·м2/кг2, m1,m2 – массы тел, r- расстояние между ними. |
m m
r |
|
2) сила тяжести, где g =9,8 м/с2 – ускорение свободного падения, m – масса тела, 3) вес тела, если υ = const, если тело движется с ускорение вверх, если тело движется с ускорение вниз, 4) сила упругости, закон Гука: где k – коэффициент упругости (жесткость), Δх – абсолютное удлинение, 5) сила трения, где μ – коэффициент трения, N – сила реакции опоры. |
2)
3)
4)
5) FTP |
1.Первую половину времени своего движения автомобиль двигался со скоростью 80км/ч, а вторую половину времени - со скоростью 60км/ч. Какова средняя скорость движения автомобиля в км/ч?
Дано:
υ1 = 80 км/ч, υ2 = 60 км/ч, t1=t2=t/2/
Найти:
υср – ?
Решение
Средняя скорость движения поезда
![]() S
S
,
t
где S – путь, t – время движения на всем участке пути.
Длина пути складывается из двух разных участков пути: на первом автомобиль движется со скоростью υ1 и длина участка пути


![]() x2 x1
x2 x1
t0=?
Решение:
![]() Определим
время встречи, тогда x1x2
Определим
время встречи, тогда x1x2
![]() 5t0 150 10t0
5t0 150 10t0
15t0 150
![]() t0
t0 ![]() 10c
10c
Место встречи
![]() х0 5t0 5 10 50м
х0 5t0 5 10 50м
Построим графики движения
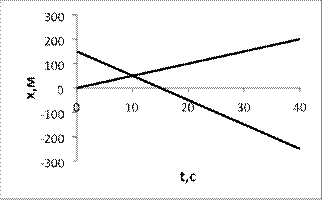
![]()
![]() Ответ: t010c, х050м
Ответ: t010c, х050м
3.Вагон движется равнозамедленно с ускорением -0,5 м/с2. Начальная скорость вагона 54 км/ч. Через сколько времени вагон остановится и какой путь пройдет до остановки?
Дано: а = -0,5 м/с2, υ0 = 54 км/ч = 15 м/с, υ=0.
Найти: t– ?
S– ?
Решение
Скорость при равноускоренном движении описывается выражением:
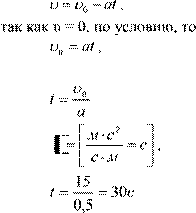 отсюда
отсюда
Путь при равнозамедленном движении вычисляется по формуле:
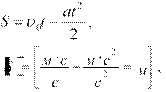
![]()
![]() S 15 30225м .
S 15 30225м .
![]() Ответ: t 30с, S 225м.
Ответ: t 30с, S 225м.
4.Лыжник спускается с горы длиной 100 м. Начальная скорость 10 м/с, ускорение
2
0,5 м/с . Сколько времени длился спуск? Дано: S = 100 м, υ0 = 10 м/с, a = 0,5 м/с2.
Найти:
t– ?
Решение
Лыжник движется равноускорено. Перемещение лыжника можно определяется по формуле:
![]() 2
2
S.
2
По условию задачи S = 100 м, υ0 = 10 м/с, a = 0,5 м/с2, тогда
 D 200
D 200
t1,2 t1
t2 48c (не удовлетворяет условию задачи)
5.Зависимость пройденного телом прямолинейного пути от времени задается
движения.
Дано:
![]() S 2t 2t2 4t3, м, t =
5 c.
S 2t 2t2 4t3, м, t =
5 c.
Найти: υ – ?
а – ?
Решение
Скорость, первая производная от перемещения ко времени dS
![]() v,
dt
v,
dt
тогда
![]() 2 4t 12t2 2 4 5 12 52 282 м
2 4t 12t2 2 4 5 12 52 282 м
с
Ускорение, первая производная от скорости материальной точки, тогда
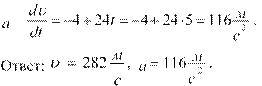
6.Автомобиль массой 1 т трогается с места и через 20 с достигает скорости 30 м/с. Найти силу тяги, если коэффициент сопротивления равен 0,05. Дано:
m=1 т=103 кг, t=20 c, υ = 30 м/с, υ0 = 0, μ = 0,05.
Найти:
Fтяг - ?
Решение
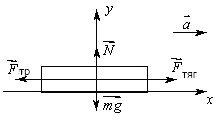
r r
На автомобиль действуют четыре силы: сила тяжести mg , сила реакции опоры N , сила
r r
тяги двигателя Fтяг и сила трения Fтр.За положительное направление оси х примем направление движения автомобиля, а ось у направим вертикально вверх. Так как движение равноускоренное, то вектор ускорения направлен в сторону движения и совпадает с направлением оси х. Для решения задачи воспользуемся вторым законом Ньютона и определением силы трения скольжения.
![]()
![]() mg , то Fтр mg , тогда
mg , то Fтр mg , тогда
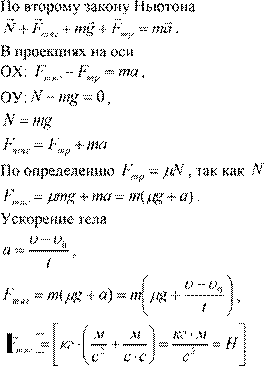 ,
,
Fтяг ![]() 2kH
2kH
Ответ: Fтяг=2кН. 7. Через блок перекинута нить, на концах которой подвешены грузы общей массой
2
10 кг. После освобождения грузы приходят в движение с ускорением 1 м/с . Найти массу каждого груза.
Дано:
m1 +m2 =10 кг, a = 1 м/с2.
Найти:
m1 – ?
m2 – ?
Решение
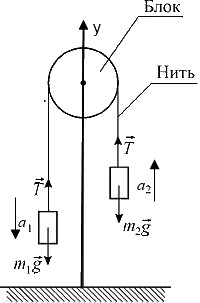
Предположим, что нить и блок невесомы и нет трения в оси блока. Тогда силы, действующие на грузы 1 и 2 со стороны нити, равны между собой (рис.) Из нерастяжимости нити следует равенство по модулю ускорений грузов 1 и 2. Запишем уравнение движение грузов. По второму закону Ньютона для каждого тела в проекции на вертикалью ось ОУ:
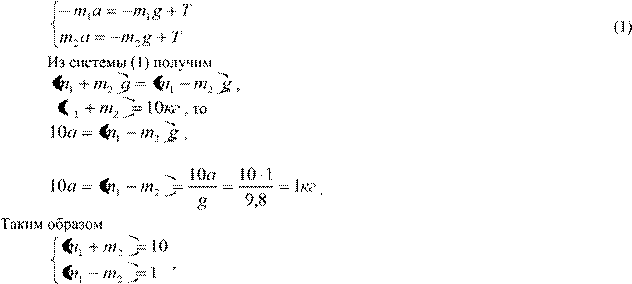 так как m отсюда
так как m отсюда
m1 10 m2
,
10 m2 m2 1
10 2m2 1,
 2m2 1 10, m2 4,5кг , m1 10 4,5 5,5кг
2m2 1 10, m2 4,5кг , m1 10 4,5 5,5кг
Ответ: m1 5,5кг m2 4,5кг .
8. Два медных шарика ( с плотностями ρ = 8,6·103кг/м3) с диаметрами D1 =4 см и D2 = 6 см находятся в соприкосновении друг с другом. Найти силу гравитационного взаимодействия этой системы.
Дано:
ρ = 8,6·103кг/м3, D1 =4 см = 0,04 м,
D2 = 6 см = 0,06 м Найти: F – ?
Решение
Из закона всемирного тяготения, сила притяжения шаров
![]() m1 m2 , (1)
m1 m2 , (1)
F G r2
где G гравитационная постоянная, r – расстояние между центрами шаров, m1 и m2 - массы шариков
 m , (2) m
(3)
m , (2) m
(3)
r (4)
F
F
9.Студент подвесил на недеформированную вертикально расположенную пружину груз массой 300 г. Пружина удлинилась на 4 см. Какой массы груз следует добавить к первому грузу, чтобы удлинение пружины стало равным 6 см? Дано:
m1 = 300 г = 0,3 кг,
Δx1 = 4 см = 0,04м,
Δx2 = 6 см = 0,06 м.
Найти: Δm– ?
Решение
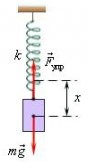
На груз, подвешенный на пружине, действуют силы: сила
тяжести mg , направленная
![]() вниз, сила
упругости Fупр,
направленная вверх.
вниз, сила
упругости Fупр,
направленная вверх.
По закону Гука сила упругости
![]() Fупр k x ,
(1)
Fупр k x ,
(1)
![]() где k – жесткость пружины,
Δх – удлинение. (знак «минус» говорит о том, что Fупр – возвращающая
сила).
где k – жесткость пружины,
Δх – удлинение. (знак «минус» говорит о том, что Fупр – возвращающая
сила).
![]() Так как груз находится в
равновесии, то Fупр k x mg , отсюда
коэффициент жесткости для груза:
Так как груз находится в
равновесии, то Fупр k x mg , отсюда
коэффициент жесткости для груза:
(2)
 после добавления
груза, массу обозначим m2, жесткость же пружины не изменилась, т.е
после добавления
груза, массу обозначим m2, жесткость же пружины не изменилась, т.е
(3)
Таким образом, чтобы удлинение пружины стало равным 6 см, следует добавить, к первому грузу массу Δm
![]() m m2 m1 0,45 0,3 0,15кг .
m m2 m1 0,45 0,3 0,15кг .
Ответ: m 0,15кг .
10.Камень массой 1,05 кг, скользящий по поверхности льда со скоростью 2,44 м/с, под действием силы трения останавливается через 10 с. Найти силу трения, считая ее постоянной.
Дано:
m = 1,05 кг, υ0 = 2,44 м/с, υ =0, t = 10 с.
Найти:
Fтр– ?
Решение
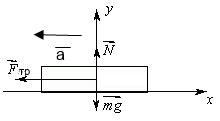
На камень действуют силы: сила тяжести mg , направленная
вниз, сила реакции опоры
![]()
![]() N , направленная вверх, сила трения Fтр,
направленная противоположно движению. По второму закону Ньютона
N , направленная вверх, сила трения Fтр,
направленная противоположно движению. По второму закону Ньютона
 тогда Задачи для
решения на занятии
тогда Задачи для
решения на занятии
1.По графику зависимости скорости движения тела от времени определить характер движения тела, начальную скорость и ускорение на каждом участке
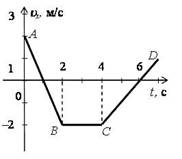
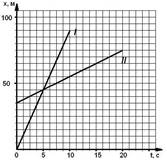
2.Найти место и время встречи двух тел 2 способами (графически и аналитически).
(Ответ: t = 5 c, х = 45 м)
![]() 3.Зависимость
пройденного телом пути от времени задается уравнением S A Bt Ct2 Dt3, где А =1 м, В = 1,5
м/с, С = 0,1 м/с2, D = 0,03 м/с3.
Определить путь, пройденный телом за 10 с и скорость в этот момент времени. (Ответ:
S = 56 м, υ = 12,5 м/с)
3.Зависимость
пройденного телом пути от времени задается уравнением S A Bt Ct2 Dt3, где А =1 м, В = 1,5
м/с, С = 0,1 м/с2, D = 0,03 м/с3.
Определить путь, пройденный телом за 10 с и скорость в этот момент времени. (Ответ:
S = 56 м, υ = 12,5 м/с)
4.
![]()
![]() Движение двух тел описывается
уравнением x1 0,75t3 2,25t2 t , x2 0,25t3 3t2 1,5t. Определить
величину скоростей этих тел и момент времени, когда ускорения их будут
одинаковы, а также значение ускорения в этот момент времени. (Ответ: υ1
= 3,81 м/с, υ2 = 4,69 м/с, а = 6,75 м/с2)
Движение двух тел описывается
уравнением x1 0,75t3 2,25t2 t , x2 0,25t3 3t2 1,5t. Определить
величину скоростей этих тел и момент времени, когда ускорения их будут
одинаковы, а также значение ускорения в этот момент времени. (Ответ: υ1
= 3,81 м/с, υ2 = 4,69 м/с, а = 6,75 м/с2)
5.
![]() Под действием силы F=10 Н
тело движется прямолинейно так, что зависимость пройденного телом пути от
времени задается уравнением S
A Bt Ct2 ,
где С=1 м/с2. Найти массу m тела. (Ответ: m = 5 кг)
Под действием силы F=10 Н
тело движется прямолинейно так, что зависимость пройденного телом пути от
времени задается уравнением S
A Bt Ct2 ,
где С=1 м/с2. Найти массу m тела. (Ответ: m = 5 кг)
![]() 6.Тело движется вниз равноускоренно
по наклонной плоскости, и зависимость пройденного пути от времени задается
уравнением S 2t 1,6t2 . Найти коэффициент
трения μ тела о плоскость, если угол наклона плоскости к горизонту равен
300.(Ответ: μ = 0,2)
6.Тело движется вниз равноускоренно
по наклонной плоскости, и зависимость пройденного пути от времени задается
уравнением S 2t 1,6t2 . Найти коэффициент
трения μ тела о плоскость, если угол наклона плоскости к горизонту равен
300.(Ответ: μ = 0,2)
7.К нити подвешен груз массой m = 500 г. Определите силу натяжения нити, если нить с грузом: 1) поднимать с ускорением 2 м/с2; 2) опускать с ускорением 2 м/с2. (Ответ: 1) Т=5,9 Н; 2) Т = 3,9 Н).
8.По графику зависимости проекции силы упругости от удлинения (рис.1.8) найдите жесткость резинового шнура.(Ответ: k≈300 Н/м)
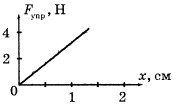
Рисунок 1.8. 9.Невесомый блок укреплен в вершине наклонной плоскости, составляющей с горизонтом угол α = 300. Гири 1 и 2 одинаковой массы m1 = m2 =1 кг соединены нитью и перекинуты через блок найти ускорение а, с которым движутся гири, и силу натяжения нити Т. Трением гири о наклонную плоскость и трением в блоке пренебречь.(Ответ: а=2,45 м/с2; Т=
7,35 Н)
10. Тело массой m = 2 кг падает в воздухе с ускорением а=9,3 м/с2. Определите силу сопротивления FС воздуха. (Ответ: FС =1Н).
1. Дайте определения кинематических характеристик поступательного движения (перемещение, траектория, путь, скорость, ускорение).
2. Какое прямолинейное движение называют равноускоренным, равнозамедленным?
3. Чем отличаются понятия средних и мгновенных скоростей и ускорений?
4. Дайте определения динамических характеристик поступательного движения (сила, масса, импульс).
5. Какова задача динамики? Сформулируйте три закона Ньютона. В каких системах отсчета они справедливы?
6. Сформулируйте закон всемирного тяготения.
7. В чем заключается физический смысл гравитационной постоянной.
8. Дайте определение веса тела.
9. Какое состояние тела называют невесомостью?
10. Куда направлена сила трения скольжения и чему она равна?
11. Какие силы называют силами упругости?
12. Сформулируйте закон Гука.
1.1 Первую
половину времени своего движения автомобиль двигался со скоростьr ю
υ1, а  вторую половину времени - со скоростью
υ км/ч. Какова средняя скорость
вторую половину времени - со скоростью
υ км/ч. Какова средняя скорость
1.2 Прямолинейное движение тела вдоль оси ОХ описывается уравнением x(t). Определите: 1) характер движения тела; 2) мгновенную скорость тела через время t от начала движения.
|
Вариант |
а |
б |
в |
г |
|
д |
|
|
x(t), м |
|
|
|
|
x |
|
|
|
t, с |
1 |
4 |
2 |
1 |
|
2 |
|
|
Вариант |
е |
ж |
з |
и |
|
к |
|
|
x(t), м |
x |
|
|
|
x |
|
t2 |
|
t, с |
3 |
5 |
10 |
15 |
|
6 |
|
1.3По графику зависимости скорости движения тела от времени построить графики
зависимости ах(t), Sx(t)υх, м/с
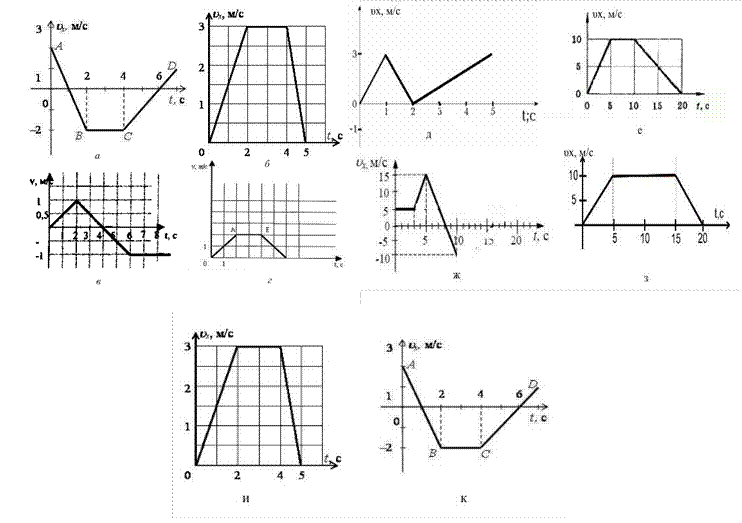
1.4 Прямолинейное движение тела вдоль оси ОХ описывается уравнением x(t). Определите: 1) характер движения тела; 2) мгновенную скорость тела через время t от начала движения.
|
Вариант |
а |
б |
в |
г |
|
д |
|
|
x(t), м |
|
|
|
|
x |
|
|
|
t, с |
1 |
4 |
2 |
1 |
|
2 |
|
|
Вариант |
е |
ж |
з |
и |
|
к |
|
|
x(t), м |
x |
|
|
|
x |
|
t2 |
|
t, с |
3 |
5 |
10 |
15 |
|
6 |
|

1.6 Автомобиль массой m движется с постоянной скоростью по прямой горизонтальной дороге. Коэффициент трения шин о дорогу равен μ. Определите силу тяги, развиваемую двигателем.

1.7 Тело скользит равномерно по наклонной плоскости с углом наклона α. Определить коэффициент трения тела о плоскость.
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
α |
30 |
20 |
25 |
35 |
40 |
30 |
45 |
35 |
25 |
40 |
1.8 По наклонной плоскости длиной L и высотой h находится груз массой m. Коэффициент трения μ. Какую силу, направленную вдоль плоскости, надо приложить к грузу, чтобы втаскивать его с ускорением а?
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
L, м |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
h, м |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
m,кг |
50 |
60 |
70 |
80 |
90 |
100 |
10 |
15 |
20 |
25 |
|
μ |
0,1 |
0,2 |
0,15 |
0,25 |
0,3 |
0,35 |
0,1 |
0,2 |
0,15 |
0,25 |
|
а, м/с2 |
0,5 |
0,7 |
1 |
1,2 |
1,4 |
1,6 |
1,5 |
1,7 |
1,9 |
2 |
1.9 С вершины наклонной плоскости высотой h и углом наклона к горизонту α начинает соскальзывать тело. Определите скорость тела в конце спуска, если коэффициент трения тела о плоскость равен μ.
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
h, м |
5 |
6 |
7 |
8 |
9 |
2 |
3 |
3.5 |
4 |
4,5 |
|
α0 |
25 |
30 |
35 |
40 |
45 |
50 |
55 |
15 |
20 |
25 |
|
μ |
0,1 |
0,2 |
0,15 |
0,25 |
0,3 |
0,35 |
0,1 |
0,2 |
0,15 |
0,25 |
1.10 Через блок перекинута нить, на концах которой подвешены грузы общей массой 10 кг. После освобождения грузы приходят в движение с ускорением 1 м/с2 . Найти массу каждого груза.
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
m, кг |
7 |
8 |
15 |
20 |
30 |
35 |
45 |
50 |
55 |
100 |
|
а, м/с2 |
2 |
1 |
1,8 |
1,5 |
2,5 |
1,5 |
2 |
2,25 |
1,75 |
2,7 |
1.11 Человек массой m поднимается в лифте равнозамедленно, вертикально вверх с ускорением а. Определите силу давления человека на пол кабины лифта.
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
m, кг |
60 |
50 |
65 |
70 |
80 |
75 |
90 |
85 |
55 |
95 |
|
а, м/с2 |
2 |
1 |
1,8 |
1,5 |
2,5 |
1,5 |
2 |
2,25 |
1,75 |
2,7 |
1.12 Как изменится сила всемирного тяготения между двумя телами, если при неизменной массе расстояние между ними увеличить в n раз.
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
n |
5 |
10 |
20 |
2 |
4 |
3 |
6 |
7 |
8 |
9 |
1.13 Тело массой m падает в воздухе с ускорением а. Найти силу сопротивления воздуха.
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
m, кг |
7 |
8 |
15 |
20 |
30 |
35 |
45 |
50 |
55 |
100 |
|
а, м/с2 |
2 |
1 |
1,8 |
1,5 |
2,5 |
1,5 |
2 |
2,25 |
1,75 |
2,7 |
1.14 Для растяжения пружины на n1 необходимо приложить силу F1. какую силу необходимо приложить, чтобы растянуть на n2 две такие пружины, соединенные параллельно?
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
n1, см |
1 |
1,5 |
2 |
2,5 |
3 |
3,5 |
4 |
4,5 |
5,5 |
6 |
|
n2, см |
0,5 |
1 |
1,5 |
2 |
2,5 |
3 |
2 |
2,5 |
1,5 |
3 |
|
F1., Н |
2 |
3 |
4 |
4.5 |
5 |
5,5 |
6 |
6,5 |
7 |
7,5 |
1.15 Сани массой m буксируют с помощью троса с жесткостью k, причем его удлинение равно Δx. С каким ускорением движутся сани, если коэффициент трения равен μ?
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
m, кг |
200 |
300 |
250 |
350 |
400 |
450 |
320 |
430 |
500 |
550 |
|
k,кН/м |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
Δx,мм |
15 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
|
μ |
0,01 |
0,02 |
0,03 |
0,04 |
0,05 |
0,015 |
0,025 |
0,035 |
0,045 |
0,055 |
Номера задач, для индивидуального решения, выбираются согласно таблице вариантов (Приложение А, таблица А1).
1.Дмитриева В.Ф. Физика для профессий и специальностей технического профиля. Сборник задач: учеб.пособие для студ. учреждений сред. проф. образования / В.Ф. Дмитриева. – 4ё–е изд., стер. – М.: Издательский центр «Академия», 2014. – 256 с.
2.Дмитриева В.Ф. Физика для профессий и специальностей технического профиля. Контрольные материалы: учеб.пособие для студ. учреждений сред. проф. образования/ В.Ф.
Дмитриева, Л. И. Васильев. – 3–е изд., стер. – М.: Издательский центр «Академия», 2014. – 112
с.
Тема: Кинематика и динамика вращательного движения твердого тела. Законы сохранения.
Цель: сформировать у курсантов физические представления о равнопеременном вращательном движении, моментах сил, моментах инерции тел, законах изменения и сохранения момента импульса, и применении данных физических представлений и законов для решения практических задач; развить мышление, память, интерес к изучению физики.
Краткие теоретические сведения
Таблица 2.1 – Основные законы и формулы
|
Физические законы, формулы, переменные |
Формулы |
|
Ускорение при криволинейном движении: 1) нормальное где R – радиус кривизны траектории, 2) тангенциальное,3) вектор полного ускорения,4) модуль полного ускорения. r |
3)a
|
|
1) угловое перемещение d . r 2) угловая скорость : где dt – интервал времени. r 3) угловое ускорение : рад рад
с с |
|
|
Равномерное вращение: 1) период вращения Т: 2) частота вращения ν: Единицы
измерения: |
2) |
|
Равноускоренное вращение β=const: 1) уравнение углового перемещения где ω0 – начальная угловая скорость 2)уравнение угловой скорости: где R – радиус – расстояние от центра вращения до материальной точки; 3) нормальное ускорение: 4) тангенциальное ускорение: 5)полное ускорение: |
|
|
Связь линейной υ и угловой скорости ω: |
|
|
1)Момент инерции J материальной точки относительно оси вращения: где mi– масса точки, ri – расстояние от оси вращения до |
1)
2) i 1 |
|
материальной точки; 2) Момент инерции системы (тела) относительно оси вращения:[1]
|
|
|||||||
|
Теорема Штейнера: где JZ– момент инерции относительно произвольной оси Z, JC– момент инерции относительно параллельной оси, проходящей через центр масс С, а – расстояние между осями. |
|
|||||||
|
1)Кинетическая энергия вращения ЕВР: где JZ - момент инерции тела относительно произвольной оси Z; ω – угловая скорость материальных точек тела. 2)Полная кинетическая энергия тела: ЕК – кинетическая энергия поступательного движения тела, m– масса тела, υ –скорость тела. |
|
|||||||
|
r r 1) Момент силы M : где r – радиус – вектор, проведенный в точку r приложения силы F ; 2) Модуль момента силы: r r где α – угол между векторами r и F , l – плечо силы.
|
|
r r r 1)
2) |
||||||
|
Основное уравнение динами вращательного движения r твердого тела: где M – момент силы, J – главный момент инерции тела(
момент инерции относительно главной оси), – угловое ускорение. |
|
|
||||||
|
1) Импульс тела:
2) |
|
|
||||||
|
r 1)Момент импульса материальной точки L : r r
–скорость точки, 2) Момент импульса твердого тела относительно оси Z: где mi – масса отдельной части твердого тела, υi – r скорость частицы, ri – радиус – вектор, ω – угловая
3) Закон сохранения момента импульса: |
LiZ |
r r r r r
2)
, r
|
||||||
|
Работа силы F: где Fs – проекция силы на ось, направленную вдоль движения, S – модуль перемещения, α - угол между вектором силы и направлением перемещения |
|
|
||||||
|
|
м |
|
|
|||||
|
Мощность N: r dA – элементарная работа, r dt – rинтервал времени, F – вектор силы, dr - перемещение, - скорость тела.
с |
r r r r dA F dr
|
|||||||
|
|
K
|
|||||||
|
Потенциальная энергия П: 3) тела, поднятого над землей на высоту h; 4) упруго деформированной пружины, жесткостью k.
|
1)
kx2 2) П 2 |
|||||||
|
Закон сохранения энергии: |
E |
|||||||
|
КПД (коэффициент полезного действия): где Апол - полезная работа, Азат - затраченная работа. |
зат |
|||||||
![]() 1. Материальная точка движется
по окружности радиусом 1 м согласно уравнению S 8t 0,2t3. Найти скорость,
тангенциальное, нормальное и полное ускорение в момент времени t = 2с.
1. Материальная точка движется
по окружности радиусом 1 м согласно уравнению S 8t 0,2t3. Найти скорость,
тангенциальное, нормальное и полное ускорение в момент времени t = 2с.
Дано:
![]() S 8t 0,2t3,
S 8t 0,2t3,
R = 1м, t = 2с.
Найти: υ – ? аτ – ? аn – ?
а –?
Решение
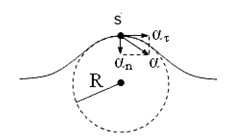
Скорость движения материальной точки равна первой производной от перемещения во времени тогда,
s/ 8 0,6t 2 ,
8 0,6 4 5,6 м
с
 Тангенциальное
ускорение найдем, взяв первую производную от скорости во времени, d м
Тангенциальное
ускорение найдем, взяв первую производную от скорости во времени, d м
a dt 1,2t 1,2 2с 2,4с2 ,
Нормальное ускорение определяется по формуле an ![]() ,
,
R
м2
![]() 31,14мс2 31,4см2
31,14мс2 31,4см2
an
Вектор полного ускоренияa равен геометрической сумме векторов at и an . Модуль ускорения же,
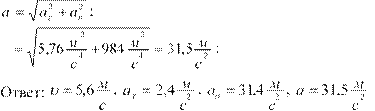 a
a
2.Точка начинает двигаться по окружности радиуса R=16 м с тангенциальным ускорением aτ=10 м/с2. 1)Чему равно полное ускорение точки через три секунды t=3с после начала движения? Решение поясните рисунком.2)Чему равна величина угловой скорости и углового ускорения при этом движении в этот момент времени? Дано: R = 16 м t= 3 с aτ = 10 м/с2
Найти:
а=? ω=? ε=?
Решение:
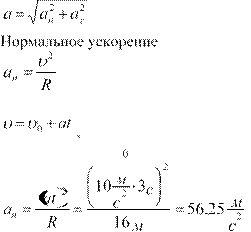 1) Полное
ускорение а можно определить по тереме Пифагора. где υ – скорость через t=
3 с. Из формулы равноускоренного движения
1) Полное
ускорение а можно определить по тереме Пифагора. где υ – скорость через t=
3 с. Из формулы равноускоренного движения
где υ – скорость точки, υ – начальная скорость точки, тогда
![]() a 56,252 м42 100 м42 57,13 м2 с с с
a 56,252 м42 100 м42 57,13 м2 с с с
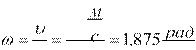 2)Угловая
скорость ω равна 30
2)Угловая
скорость ω равна 30
.
R 16м с
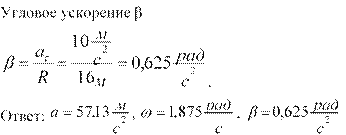
3.Колесо, вращаясь равноускорено, достигло угловой скорости ω=20 рад/с и через N=10 оборотов после начала вращения. Найти угловое ускорение β колеса. Дано:
ω=20 рад/с, N=10
Найти: β – ?
Решение
Запишем уравнения движения для равноускоренного вращательного движения:
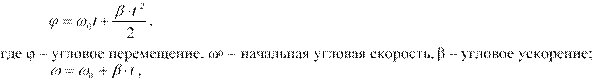
где ω – угловая скорость.
Так как по условию задачи ω0 = 0, тогда уравнения движения примут вид:
 ,
(1)
,
(1)
(2)
Выразим из уравнения (1) угловое ускорение ε
(3)
2 N , где N – число оборотов колеса, тогда уравнение (3) можно
(4)
отсюда

4.Найти радиус R вращающегося колеса, если известно, что линейная скорость v1 точки, лежащей на ободе, в 2,5 раза больше скорости v2 точки, лежащей на расстоянии r=5 см ближе к оси колеса.
Дано:
![]() 2,5,
2,5,
r=5 см = 5·10-2м. Найти: R– ?
Решение
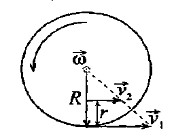
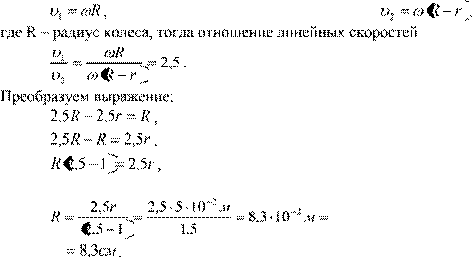 Поскольку
угловые скорости всех точек колеса одинаковы, то величины линейных скоростей
будут определяется выражениями: отсюда
Поскольку
угловые скорости всех точек колеса одинаковы, то величины линейных скоростей
будут определяется выражениями: отсюда
8,3см. Ответ: R
5. Колесо, вращаясь равнозамедленно, уменьшило за время 1 мин частоту вращения от 300 об/ мин до 180 об/мин. Найти число оборотов, сделанных колесом за это время.
Дано:
t = 1 мин =60 с, ν1 = 300 об/ мин = 5 об/с, ν2 = 180 об/мин = 3 об/с.
Найти:
N– ?
Решение
Число оборотов N, сделанных колесом за время t:
 где φ – угол поворота
за время t, равный при равнозамедленном движении ω0 – начальная
угловая скорость, β – угловое ускорение.
где φ – угол поворота
за время t, равный при равнозамедленном движении ω0 – начальная
угловая скорость, β – угловое ускорение.
,
 N ,
N ,
N
Ответ: N
k=40 см = 0,4 м, m= 0,6 кг,
![]() Bt3 ,
Bt3 ,
А=1 рад/с, В=0,1 рад/с3, t = 2 с.
Найти: М – ?
Решение
Согласно уравнению динамики вращательного движения твердого тела:
M ![]() , (1)
где М – вращающий момент, β – угловое ускорение, J – момент инерции
стержня.
, (1)
где М – вращающий момент, β – угловое ускорение, J – момент инерции
стержня.
Момент инерции прямого тонкого стержня длиной k, вращающегося вокруг своей оси, проходящей через середину стержня
J mk2 . (2)
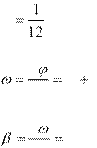 По
определению угловая скорость d A 3Bt2 . dt
По
определению угловая скорость d A 3Bt2 . dt
Угловое ускорение d
6Bt .
dt
![]() В момент
времени t = 2 с, 6Bt ,
тогда с учетом (2)
В момент
времени t = 2 с, 6Bt ,
тогда с учетом (2)
![]()
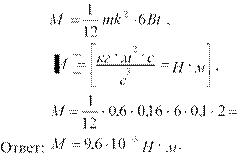 0,0096 9,6
10 3Н м.
0,0096 9,6
10 3Н м.
7.Чему равен момент инерции J тонкого прямого стержня длиной L=0,5 м и массой m=0,2 кг относительно оси, перпендикулярной к его длине и проходящей через точку стержня, которая удалена на l=0,15 м от одного из его концов. Дано: L=0,5 м m=0,2 кг l=0,15 м
Найти:
J-?
Решение:
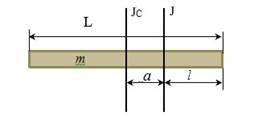
Момент инерции стержня находим по теореме Штейнера. ![]() ma2,
ma2,
где J – момент инерции тела относительно произвольной оси, JC– момент инерции относительно параллельной оси проходящей через его центр масс, m – масса стержня, а – расстояние между осями.
Момент инерции стержня
JmL2 ,
![]() где L – длина стержня. al
где L – длина стержня. al
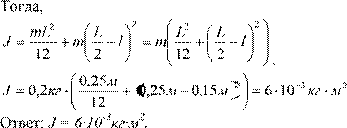
0
8.Шар скатывается по наклонной плоскости с углом наклона α=30 . Какую скорость v будет иметь центра шара относительно наклонной плоскости через t=1,5 с.
Если его начальная скорость была равно нулю? Дано:
α=300, t=1,5 с, υ0 = 0 м/с.
Найти: υ– ?
Решение:
По закону сохранения энергии
 где J mR
− момент инерции шара,
где J mR
− момент инерции шара,![]() − связь линейной и угловой
скорости,h=lsinα, R
− связь линейной и угловой
скорости,h=lsinα, R
l − так как движение происходит под действием постоянной силы, то движение 2 равноускоренное.
![]()
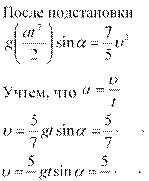 , после
замены, имеем 9,8 1,5sin 300
5,3 м
с
, после
замены, имеем 9,8 1,5sin 300
5,3 м
с
Ответ: 9,8 1,5sin 300 5,3 м
7 7 с
3 (рад). Момент инерции маховика 5
9.Маховик вращается по закону φ = 10 t + t
2 кг·м . Определить момент силы, действующий на маховик, в момент времени 1с.
Дано: φ = 10 t + t3рад, J=5 кг·м2, t=1c,
Найти: М=?
Решение:
Из основного уравнения динамики для вращательного движения
M J ,
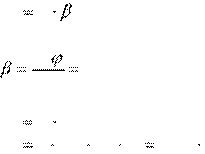 где
момент инерции J, β – угловое ускорение. d2 2
6t , dt
где
момент инерции J, β – угловое ускорение. d2 2
6t , dt
Тогда момент силы
M J 6t Н M 6 5кг м2 1с 30Н м
Ответ: М=30 Н·м.
10.Однородный стержень длиной l=1 м и массой m=0,5 кг вращается в вертикальной плоскости вокруг горизонтальной оси, проходящей через середину стержня.
С каким угловым ускорением ε вращается стержень, если на него действует момент сил М=98,1мН·м?
Дано:
l=1 м, m=0,5 кг,
М=98,1мН·м = 98,1·10-3Н·м. Найти: β– ?
Решение
Из основного уравнения динамики вращательного движения момент сил равен:

![]() 11. Колесо
радиуса 0,2 м с равномерно распределенной по ободу массой 5 кг вращается относительно
неподвижной оси, перпендикулярной его плоскости
и проходящей через его центр, так, что зависимость угла поворота колеса от
времени задается уравнением = 5+4t2–t3 (рад). Определить
для момента времени t = 1 с момент импульса L колеса; момент M действующей
силы; кинетическую энергию T колеса. Дано: R = 0,2 м, m = 5
кг,
11. Колесо
радиуса 0,2 м с равномерно распределенной по ободу массой 5 кг вращается относительно
неподвижной оси, перпендикулярной его плоскости
и проходящей через его центр, так, что зависимость угла поворота колеса от
времени задается уравнением = 5+4t2–t3 (рад). Определить
для момента времени t = 1 с момент импульса L колеса; момент M действующей
силы; кинетическую энергию T колеса. Дано: R = 0,2 м, m = 5
кг,
![]() = 5+4t2–t3
(рад), t = 1 с.
= 5+4t2–t3
(рад), t = 1 с.
Найти: L – ?
M – ? T – ?
Решение
Угловая скорость вращения равна первой производной от угла поворота по времени:
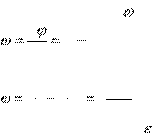 d 8t 3t2(рад/с), dt
d 8t 3t2(рад/с), dt
для момента времени t = 1 с
8 1 3 12 5 рад .
с
Угловое ускорение вращения равно первой производной от угловой скорости по времени:
![]() ,
,
dt
для момента времени t = 1 с
![]() 8 6 1 2 рад2
8 6 1 2 рад2
с
![]() При
вращении абсолютно твердого тела вокруг неподвижной оси каждая точка тела
движется по окружности постоянного радиуса Ri, со скоростью υi, перпендикулярной
радиусу. Момент импульса отдельной частицы равен Li mi i Ri
При
вращении абсолютно твердого тела вокруг неподвижной оси каждая точка тела
движется по окружности постоянного радиуса Ri, со скоростью υi, перпендикулярной
радиусу. Момент импульса отдельной частицы равен Li mi i Ri
Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц:

На основании основного уравнения динамики вращательного движения
 М
М
М
Т
Т
Т
12.Горизонтальная платформа массой m = 80 кг и радиусом R= 1м вращается с угловой частотой ν1= 20 об/мин. В центре платформы стоит человек и держит в расставленных руках гири. С какой частотой ν2 будет вращаться платформа, если человек опустит руки, уменьшит свой момент от J1=2,94 до J2=0,98 кг·м2? Считать платформу однородным диском.
Дано:
m = 80 кг, R= 1м, ν1= 20 об/мин = 1/3 об/с,
J1=2,94 кг·м2, J2=0,98 кг·м2.
Найти:
ν2 – ?
Решение
Момент импульса платформы и человека с расставленными руками

![]() 13. Молот массой m1=200
кг падает на поковку, масса m2 которой вместе с наковальней равна
2500 кг. Скорость 1
молота в момент удара равна 2 м/с. Найти: кинетическую энергию молота в момент
удара; энергию, переданную фундаменту; энергию, затраченную на деформацию
поковки; КПД удара молота о поковку. Удар считать абсолютно неупругим.
13. Молот массой m1=200
кг падает на поковку, масса m2 которой вместе с наковальней равна
2500 кг. Скорость 1
молота в момент удара равна 2 м/с. Найти: кинетическую энергию молота в момент
удара; энергию, переданную фундаменту; энергию, затраченную на деформацию
поковки; КПД удара молота о поковку. Удар считать абсолютно неупругим.
Дано:
m1=200 кг, m2 = 2500 кг,
1
![]() = 2 м/с.
= 2 м/с.
Найти:
Т1 – ?
Т – ?
η – ?
Решение.
Кинетическую энергию молота в момент удара найдем по формуле:
m1 12 200кг 22 мс22 400Дж.
T1
2 2
Запишем закон сохранения импульса при неупругом ударе: m1 1 m2 2 (m1 m2) ,
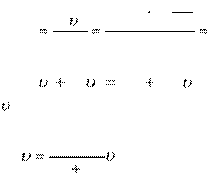
![]() где 2 – скорость поковки перед
ударом, - скорость молота и поковки после удара. Так как наковальня с поковкой
покоились, то 2=0. Следовательно, m1 m1 m2 1.
где 2 – скорость поковки перед
ударом, - скорость молота и поковки после удара. Так как наковальня с поковкой
покоились, то 2=0. Следовательно, m1 m1 m2 1.
Энергия, переданная фундаменту, равна кинетической энергии системы после удара:
![]() (m1 m2)
2 m12 12 m1 T 200кг 400Дж 29,6
(m1 m2)
2 m12 12 m1 T 200кг 400Дж 29,6
T2 1 Дж .
2 (m1 m2) 2 (m1 m2) 2700кг
На деформацию поковки идет разность кинетических энергий:
Т = Т1 - Т2 = 370 Дж.
КПД удара равно отношению энергии, потраченной на деформацию поковки, к первоначальной энергии, т.е.
![]() Т 370Дж
Т 370Дж
0,926 или 92,6%.
Т1 400Дж
Ответ: 400 Дж; 29,6 Дж; 370 Дж; 92,6%.
1.Найти угловую скорость ω: а) суточного вращения Земли; б) часовой стрелки на часах; в) минутной стрелки на часах; г) искусственного спутника Земли, движущегося по круговой орбите с периодом вращения Т=88 мин. Какова линейная скорость υ движения этого искусственного спутника, если известно, что его орбита расположена на расстоянии h = 200 км от поверхности Земли? (Ответ: а) ω = 72,7·10-6рад/с; б) ω = 145,4·10-6рад/с; в) ω = 1,74·10-6рад/с; г) ω = 1,19·10-3рад/с, υ = 7,83км/ч.
![]() 2.Зависимость
угла поворота от времени для точки, лежащей на ободе колеса радиуса R, задается
уравнением t3 0,5t2 2t 1. К концу
третьей секунды эта точка получила
2.Зависимость
угла поворота от времени для точки, лежащей на ободе колеса радиуса R, задается
уравнением t3 0,5t2 2t 1. К концу
третьей секунды эта точка получила
нормальное ускорение, равное 153 м/с2. Определите радиус колеса. (Ответ: R =0,15 м)
3.Найти момент инерции J и момент импульса L земного шара относительно оси
вращения.(Ответ: J = 97,3·1036кг·м2; L = 7,07·1033кг·м/с2)
4. На вал массой 10 кг намотана нить, к концу которой привязан груз массой 2 кг. Определить ускорение груза, опускающегося под действием силы тяжести. Трения нет. (Ответ: а= 2,8 м/с2)
5.Диск диаметром D = 60 см и массой m = 1 кг вращается вокруг оси, проходящей через центр перпендикулярно к его плоскости с частотой ν = 20 об/с. какую работу А надо совершить, чтобы остановить диск? (Ответ: А=355 Дж)
6.Вентилятор вращается с частотой ν = 900 об/мин. После выключения вентилятор, вращаясь равнозамедленно, сделал до остановки N = 75 об. Работа сил торможения А =44,4 Дж. Найти момент инерции J вентилятора и момент сил торможения М. (Ответ: J = 0,016 кг·м2; М=94·10-3Н·м).
7. Граната, летящая со скоростью υ = 10 м/с, разорвалась на два осколка. Больший осколок, масса которого составляла 0,6 массы всей гранаты, продолжал двигаться в прежнем направлении, но с увеличенной скоростью u1 = 25 м/с. Найти скорость u2 меньшего осколка. (Ответ: u2 = -12,5 м/с).
8. Найти кинетическую энергию велосипеда, едущего со скоростью υ = 9 км/ч. Масса велосипедиста вместе с велосипедом m = 78 кг, причем на колеса приходится масса m1 = 3 кг.
Колеса считать тонкими обручами.(Ответ: К =253 Дж)
9. Определите скорость поступательного движения сплошного цилиндра, скатившегося с наклонной плоскости высотой h= 20см.(Ответ:1,63 м/с)
10.Горизонтальная платформа массой m = 100 кг вращается вокруг вертикальной оси, проходящей через центр платформы, с частотой ν1 = 10 об/мин. Человек массой m0 = 60 кг стоит при этом на краю платформы. С какой частотой ν2 начнет вращаться платформа, если человек перейдет от края платформы к ее центру? считать платформу однородным диском, а человека – точечной массой.(Ответ: ν2 = 22 об/мин)
1. Сформулируйте понятия углового перемещения, угловой скорости и углового ускорения.
2. Запишите формулы, связывающие линейные и угловые величины.
3. Какая физическая величина называется моментом силы? Назовите единицы измерения момента силы в Системе интернациональной измерения физических величин.
4. Какая физическая величина называется моментом импульса? Назовите единицы измерения момента импульса в Системе интернациональной измерения физических величин.
5. Сформулируйте правило правого винта для определения направления векторов момента силы и момента импульса.
6. Выведите основное уравнение динамики вращательного движения. При каких условиях это уравнение выполняется?
7. Выведите закон сохранения момента импульса. При каких условиях этот закон выполняется?
8. Дайте определение момента инерции твердого тела.
9. Сформулируйте теорему Гюйгенса-Штейнера.
10. Чему равна кинетическая энергия вращательного движения?
11. Сформулируйте определение работы силы. В каких единицах измеряется работа?
12. При каких условиях работа силы положительная? отрицательная? равна нулю?
13. Дайте определение мощности. В каких единицах измеряется мощность?
14. Сформулируйте определение энергии. В каких единицах измеряется энергия?
15. Дайте определение кинетической энергии?
16. Приведите определение потенциальной энергии системы тел?
17. Чему равна энергия потенциальная энергия упругодеформированного тела?
18. Чему равна полная механическая энергия системы тел?
19. При каких условиях полная механическая энергия системы сохраняется?
20. Какой удар называют абсолютно неупругим? упругим?
2.1 Точка движется по окружности радиусом R с постоянным тангенциальным ускорением аτ . Найти тангенциальное ускорение точки, если известно, что к концу n –го оборота после начала движения линейная скорость точки υ
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
R, см |
10 |
12 |
14 |
15 |
17 |
19 |
20 |
22 |
24 |
25 |
|
n,об |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
υ, см/с |
79,2 |
80 |
82,6 |
87,4 |
90,2 |
96,4 |
100,1 |
112,5 |
115,8 |
120,3 |
2.2 Колесо, вращаясь равноускоренно, через время t после начала вращения приобретает частоту ν. Найти угловое ускорение ε колесо и число оборотов N колеса за это время.
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
t, мин |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
ν,об/мин |
500 |
600 |
550 |
650 |
700 |
800 |
900 |
1000 |
1100 |
1200 |
2.3 Точка движется по окружности радиусом R с постоянным тангенциальным ускорением аτ. Через какое время t после начала движения нормальное ускорение аn точки будет: а) равно тангенциальному; б) вдвое больше тангенциального?
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
R,см |
10 |
15 |
20 |
12 |
17 |
22 |
25 |
28 |
14 |
21 |
|
аτ., см/с2 |
0,4 |
0,3 |
0,2 |
0,5 |
0,6 |
0,45 |
0,35 |
0,7 |
0,55 |
0,65 |
![]() 2.4 Точка движется по
окружности радиусом R. Зависимость пути от времени задается уравнением S A
Ct 3 .
Найти нормальное аn и тангенциальное аτ
ускорения точки в момент, когда линейная скорость точки υ.
2.4 Точка движется по
окружности радиусом R. Зависимость пути от времени задается уравнением S A
Ct 3 .
Найти нормальное аn и тангенциальное аτ
ускорения точки в момент, когда линейная скорость точки υ.
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
С, см/с3 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1 |
|
R,см |
1 |
1,5 |
2 |
1,2 |
1,7 |
2,2 |
2,5 |
2,8 |
1,4 |
2,1 |
|
υ, м/с |
40 |
46 |
22 |
50 |
52 |
53 |
30 |
28 |
38 |
48 |
2.5 На барабан массой m0 намотан шнур, к концу которого привязан груз массой m. Найти ускорение а груза. Барабан считать однородным цилиндром. Трением пренебречь.
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
m0,кг |
10 |
15 |
20 |
12 |
17 |
22 |
25 |
28 |
14 |
21 |
|
m, кг |
2 |
4 |
4,5 |
3 |
3,5 |
5 |
4,7 |
5.7 |
3,8 |
2,9 |
2.6 Определите момент инерции J тонкого однородного стержня длиной l и массой m, относительно оси, перпендикулярной стержню и проходящей через: 1) конец стержня; 2) точку, отстоящую от конца стержня на 1/3 его длины.
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
m, г |
200 |
300 |
250 |
350 |
400 |
450 |
150 |
100 |
270 |
330 |
|
l, см |
40 |
46 |
22 |
50 |
52 |
53 |
30 |
28 |
38 |
48 |
2.7 Диск массой m катится без скольжения по горизонтальной плоскости со скоростью υ. Найти кинетическую энергию К диска.
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
m,кг |
1 |
1,5 |
2 |
1,2 |
1,7 |
2,2 |
2,5 |
2,8 |
1,4 |
2,1 |
|
υ, м/с |
4 |
4,6 |
2,2 |
5 |
5,2 |
5,3 |
3 |
2,8 |
3,8 |
4,8 |
![]() 2.8 Шар радиусом R и массой
m вращается вокруг оси симметрии согласно уравнению A Bt2 Ct3, А, В, С – постоянные.
Определите момент сил М для момента времени t
2.8 Шар радиусом R и массой
m вращается вокруг оси симметрии согласно уравнению A Bt2 Ct3, А, В, С – постоянные.
Определите момент сил М для момента времени t
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
R, см |
10 |
12 |
15 |
18 |
20 |
22 |
25 |
27 |
30 |
32 |
|
m,кг |
5 |
7 |
9 |
10 |
11 |
12 |
15 |
17 |
19 |
20 |
|
В, рад/с2 |
2 |
2,2 |
2,4 |
2,5 |
2,7 |
3 |
3,2 |
3,5 |
3,7 |
4 |
|
С, рад/с3 |
-0,5 |
-0,7 |
-,08 |
-1 |
-04 |
-1,1 |
-1,2 |
-1,4 |
-1,5 |
-1,7 |
|
t, с |
3 |
4 |
2 |
5 |
6 |
1 |
5 |
4 |
3 |
2 |
2.9 Маховик, момент инерции которого J вращается с угловой скоростью ω. Найти момент сил торможения М, под действием которого маховик останавливается через время t с. Маховик считать однородным диском.
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
J, кг·м2 |
63,6 |
55,4 |
48,2 |
61,7 |
59,3 |
71,2 |
58,4 |
49,5 |
64,9 |
53,1 |
|
ω, рад/с |
31,4 |
29,4 |
38,5 |
41,6 |
34,6 |
44,7 |
23,9 |
34,5 |
41 |
39 |
|
t, с |
20 |
10 |
15 |
30 |
25 |
16 |
24 |
26 |
18 |
19 |
2.10 Какова энергия упругой деформации пружины при ее сжатии на Δх1, если для ее сжатия на Δх2необходима сила F?
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
Δх1, см |
10 |
12 |
15 |
17 |
20 |
22 |
25 |
27 |
30 |
33 |
|
Δх2, см |
1 |
1,5 |
2 |
2,5 |
3 |
3,5 |
4 |
4,5 |
5 |
5,5 |
|
F, Н |
100 |
150 |
200 |
250 |
270 |
300 |
330 |
350 |
400 |
450 |
2.11 Шар массой m1 движется со скоростью υ1 и сталкивается с покоящимся шаром массой m2. Какая работа будет совершена при деформации шаров? Удар считайте абсолютно неупругим, прямым, центральным.
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
m1, кг |
1 |
1,2 |
1,5 |
1,7 |
2 |
2,2 |
2,5 |
2,7 |
3 |
3,3 |
|
m2, кг |
3 |
3,2 |
2,7 |
2,5 |
3,5 |
4 |
4,2 |
4,5 |
5 |
5,5 |
|
υ1, м/с |
1 |
1,5 |
2 |
2,5 |
2,7 |
3 |
3,3 |
3,5 |
4 |
4,5 |
2.12 Человек массой М кг и тележка массой m движутся навстречу друг другу. Скорость человека υ1ч, скорость тележки – υ2. Человек прыгает на тележку и останавливается. Найти скорость тележки вместе с человеком.

2.13 При горизонтальном полете со скоростью υ снаряд массой m разорвался на две части. Большая часть массой m1 получила скорость u1 в направлении полёта снаряда. Определите модуль и направление скорости u2 меньшей части снаряда.

2. 14.Из пружинного пистолета был произведен выстрел пулей массой m. Определить скорость пули при вылете её из пистолета, если пружина была сжата на Δx, а её жесткость k
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
m, г |
5 |
6 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
|
Δx, см |
3 |
3,2 |
2,7 |
2,5 |
3,5 |
4 |
4,2 |
4,5 |
5 |
5,5 |
|
k, Н/м |
100 |
150 |
200 |
250 |
270 |
300 |
330 |
350 |
400 |
450 |
2.15. Горизонтальная платформа массой m и радиусом R вращается с частотойν1. В центре платформы стоит человек и держит в расставленных руках гири. С какой частотой ν2 будет вращаться платформа, если человек, опустив руки, уменьшит свой момент инерции от J1 до J2. Считать платформу однородным диском.
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
m, кг |
80 |
70 |
55 |
60 |
65 |
85 |
75 |
62 |
74 |
84 |
|
R, м |
2 |
3 |
1 |
1,5 |
1,7 |
2 |
3,5 |
2,5 |
1,3 |
1,2 |
|
ν1, об/мин |
10 |
20 |
15 |
25 |
30 |
35 |
17 |
24 |
31 |
25 |
|
J1, кг·м2 |
2,4 |
2,5 |
3 |
3,5 |
4 |
4,5 |
3,3 |
3,2 |
4,5 |
4 |
|
J2, кг·м2 |
1 |
0,98 |
1,72 |
1,4 |
1,98 |
2 |
1,3 |
1,6 |
2,3 |
2 |
Номера задач, для индивидуального решения, выбираются согласно таблице вариантов
(Приложение А, таблица А1).
1.Дмитриева В.Ф. Физика для профессий и специальностей технического профиля. Сборник задач: учеб.пособие для студ. учреждений сред. проф. образования / В.Ф. Дмитриева. – 4ё–е изд., стер. – М.: Издательский центр «Академия», 2014. – 256 с.
2.Дмитриева В.Ф. Физика для профессий и специальностей технического профиля.
Контрольные материалы: учеб.пособие для студ. учреждений сред. проф. образования/ В.Ф.
Дмитриева, Л. И. Васильев. – 3–е изд., стер. – М.: Издательский центр «Академия», 2014. – 112 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №3
Тема: Молекулярно - кинетическая теория идеальных газов
Цель: закрепить знания об идеальном газе, изопроцессах; сформировать умение решать задачи на применение уравнения состояния идеального газа; привить интерес к решению задач по физике.
Краткие теоретические сведения
Таблица 3.1 – Основные законы и формулы
|
Физические законы переменные |
Формулы |
|
Число ν молей вещества, m – масса, μ – молярная масса |
|
|
Масса m0 одной молекулы газа, NA – число Авогадро |
m0
|
|
Число молекул N в некоторой массе т газа |
N |
|
Закон Дальтона для смеси газов: где р – давление смеси газов; рn – давление n – го компонента смеси (парциальное давление); n – число компонентов смеси. |
|
|
Основное уравнение молекулярно – кинетической теории газов: где р – давление газа; m0 – масса одной N
число молекул в единице объема, средняя квадратичная скорость молекул |
1
3 |
|
Средняя кинетическая энергия Ек теплового движения молекул газа; i – число степеней свободы, k – постоянная Больцмана |
i
2 |
|
Формула связывающая давление газа и среднюю кинетическую энергию поступательного движения молекул: |
|
|
Уравнение Менделеева – Клапейрона, р – давление, V – объём, R – универсальная газовая постоянная, Т - температура |
m
|
|
Уравнение Клапейрона(уравнение состояния газа): |
T1 T2
|
|
Изопроцессы: 1)изотермический процесс m = const, Т= const; 2) изобарный процесс m = const,р= const; 3) изохорный процесс m = const,V= const;
|
1) p1V1 p2V2 ; V T 2) 1 1 ;
3) 1 1 p2 T2 |

Примеры решения задач
1.Найти массу атомов: 1) водорода; 2) гелия. 3) молекулы СО2 Дано:
1) водород (Н2)
2) гелия (Не)
3) молекулы СО2 Найти:
1) m0 (Н2) – ?, 2) m0 (Не) – ?, 3) m0 (СО2) – ?
![]() 0
0
27кг ,
![]()
![]()
![]() Ответ: m0 Н2 3,3 10 27кг , m0 Не 6,6 10 27кг , m0 Не 73 10 27кг
Ответ: m0 Н2 3,3 10 27кг , m0 Не 6,6 10 27кг , m0 Не 73 10 27кг
2. Какова средняя кинетическая энергия молекулы газа, если его давление равно
5.104 Па, а в объеме 12 л содержится 6.1024 молекул? Дано:
р=5.104 Па
V=12 л=12·10-3м3
N=6·1024
Найти: Ek=?
Решение:
Из основного уравнения молекулярно-кинетической теории

3
3 Определите массу газа, объем которого 5 м , давление 3 атм, а средняя квадратичная скорость молекул 1500 м/с. Дано:
V=5 м3,
Р=3 атм = 3·105Па, ![]() 1500м/с .
1500м/с .
Найти: m– ?
Решение
Средняя квадратичная скорость молекул
![]() , (1)
, (1)
где R – универсальная газовая постоянная, T – термодинамическая температура, μ – молярная масса газа.
Возведем к квадрат уравнение (1) получим:
![]() .
(2)
.
(2)
Из уравнение Менделеева – Клапейрона
или
(3)

4. Газ при температуре t=150С и давлении р= 200 кПа имеет плотность ρ = 0,34
3 кг/м . Найти молярную массу μ газа.
Дано:
t=150С, Т=273+15=288 К, р= 200 кПа=2·105Па, ρ = 0,34 кг/м3. Найти: μ – ?
Решение
Из уравнения Менделеева – Клапейрона m
pV RT ,
где V – объем газа, R – универсальная газовая постоянная,
m 1 p RT .
V
![]() Плотность газа m
Плотность газа m
,
Тогда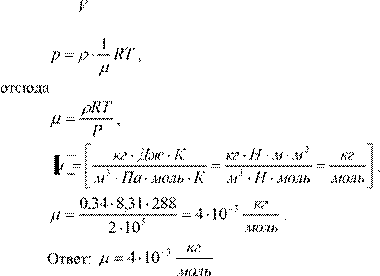
5. Какой объем занимает смесь азота массой 2 кг и гелия массой 1 кг при нормальных условиях. Чему равна молярная масса смеси? Дано:
m1 = 2 кг, m2 = 1 кг, Т = 273К, р = 105Па, μ1(N2)=28·10-3кг/моль, μ2(Не) = 4·10-3кг/моль. Найти: V– ?
μ– ?
Решение
Объем смеси газов
![]() V V1 V2,
V V1 V2,
где V1 – объем азота, V2 – объем гелия. Объемы газов найдем из уравнения Менделеева – Клапейрона: m
![]() pV1 1 RT ,
pV1 1 RT ,
M1
m
pV2 2 RT , M2
отсюда
![]() V1RT ,
V1RT ,
V2RT ,
где R – универсальная газовая постоянная, р – давление газа, Т – термодинамическая температура, тогда
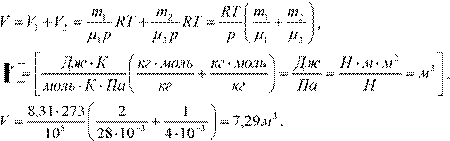
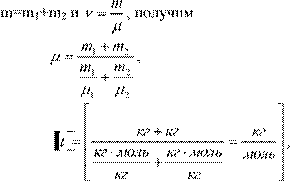
Молярная масса смеси μ есть отношение массы смеси m к количеству вещества смеси
ν,т.е
m
![]() . v
. v
Масса смеси равна сумме масс компонентов смеси m=m1+m2. Количество вещества m
![]() смеси
равно сумме количеств вещества компонентов. Подставив в формулу , выражения
смеси
равно сумме количеств вещества компонентов. Подставив в формулу , выражения
v
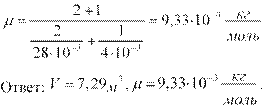
6. Баллон ёмкостью 10 л содержит водород массой 1 г. Найти среднюю длину свободного пробега молекул.
Дано: Н2 d=0,28·10-9м
V=10 л=0,01м3 m=1 г=10-3кг Найти:
λ=?
Решение:
Средняя длина свободного пробега молекулы
1
, (1)
2 d 2n
![]() где d
– эффективный диаметр молекул водорода; n – концентрация молекул.
где d
– эффективный диаметр молекул водорода; n – концентрация молекул.
N
n
V
Так как
N m
![]() Na M mNa n
Na M mNa n
MV
М=0,002 кг/моль – молярная масса водорода, Na=6,022·1023 – число Авогадро.
Тогда,
![]()
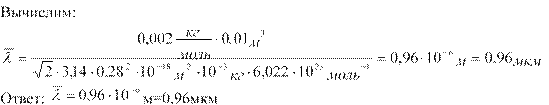
![]() 7. Определить среднее
число соударений в секунду z и длину свободного пробега молекул
водорода при температуре t = 270С и давлении Р = 1·10-3
мм.рт.ст. Дано:
7. Определить среднее
число соударений в секунду z и длину свободного пробега молекул
водорода при температуре t = 270С и давлении Р = 1·10-3
мм.рт.ст. Дано:
t = 270С,
Р = 1·10-3 мм.рт.ст. = 133,3·10-3 Па, d = 0,23·10-9 м,
М(Н2) = 2·10-3 кг/моль Найти:
![]() z –
?,
z –
?,
–?
Решение
Средняя длина свободного пробега молекулы
![]() , (1)
, (1)
где d – эффективный диаметр молекул водорода; n – концентрация молекул. Из основного уравнения молекулярно – кинетической теории
![]() имеем p
имеем p
n , (2) kT
где p – давление, k – постоянная Больцмана, T – термодинамическая температур., Т = 273+27 = 300 К
Тогда, с учетом (2), выражение (1) можно записать в виде
 (3)
(3)
(4)
![]() Средняя арифметическая скорость вычисляется по формуле
Средняя арифметическая скорость вычисляется по формуле
, (5)
где R – универсальная газовая постоянная, T– термодинамическая температура, M – молярная масса водорода.
Таким образом, с учетом (5) запишем выражение (4)
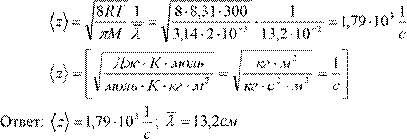
1. Сколько молекул газа содержится в колбе вместимостью 500 см3 при нормальных условиях? (Ответ: 1,34·1022)
2. Сколько молекул содержится при нормальных условиях в 1 кг кислорода? Плотность кислорода при нормальных условиях приять равной 1,43 кг/м3. (Ответ: 1,9·1025)
3. Определите давление водорода, если средняя квадратичная скорость его молекул 800 м/с, а его плотность 2,4 кг/м3. (Ответ: 0,512 МПа).
4.Найти температуру газа при давлении 100 кПа и концентрации молекул 1025м-3. (Ответ: 724 0К)
5.Найти среднюю квадратичную скорость молекул воздуха при температуре 170С. молярная масса воздуха 0,029 кг/моль. (Ответ: 500 м/с)
6. Найти среднюю длину свободного пробега молекул углекислого газа при температуре 1000С и давлении 13,3 Па. Диаметр молекул углекислого газа 0,32 нм.(Ответ:850 мкм)
7. Найти среднее число столкновений в единицу времени молекул углекислого газа при температуре 1000С, если средняя длина свободного пробега 870 мкм. (Ответ: 4,87·105 с-1)
1. Сформулируйте основные положения молекулярно – кинетической теории.
2. Что такое относительная молекулярная масса?
3. Что называют количеством вещества? Единица измерения.
4. Каков физический смысл постоянной Авогадро?
5. В чем измеряется молярная масса?
6. Какой газ называется идеальным?
7. Что такое давление? Чем оно обусловлено?
8. Что называется термодинамическим процессом? изопроцессом?
9. Сформулируйте законы Бойля – Мариотта, Гей – Люссака, Шарля.
10. Какая температура называется термодинамической?
11. Какой физический смысл имеет газовая постоянная и постоянная Больцмана?
12. Какова связь между кинетической энергией поступательного движения молекул газа и его термодинамической температурой?.
13. Какую величину называют длиной свободного пробега молекул?
3.1.Вычислить массу m0 одной молекулы газа.
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
газ |
О3 |
СН4. |
О2 |
N2 |
CO2 |
He |
Kr |
Xe |
Ar |
Ne |
3.2.Определить массу m газа, взятого в количестве ν(моль).
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
газ |
О3 |
СН4. |
О2 |
N2 |
CO2 |
He |
Kr |
Xe |
Ar |
Ne |
|
ν, моль |
100 |
50 |
20 |
35 |
40 |
55 |
75 |
120 |
110 |
90 |
3.3.Какое давление создает m газа, занимающая объем V при температуре Т
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
m, г |
5 |
4 |
3 |
2 |
6 |
2,5 |
3,5 |
4,5 |
5,5 |
6,5 |
|
V, см3 |
765 |
786 |
790 |
779 |
755 |
756 |
800 |
732 |
880 |
765 |
|
Т, 0С |
8 |
5 |
7 |
6 |
4 |
9 |
10 |
2 |
3 |
11 |
|
газ |
|
|
|
|
|
|
|
|
|
|
3.4.Сосуд откачен до давления Р, температура воздуха t. Найти плотность воздуха в
сосуде.
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
Р, нПа |
1,33 |
2 |
2,4 |
2,7 |
1 |
1,5 |
3 |
3,2 |
3,7 |
4 |
|
t, 0С |
10 |
12 |
15 |
17 |
20 |
9 |
8 |
7 |
6 |
5 |
3.5.Определить сколько киломолей и молекул газа содержится в объеме V под давлением Р при температуре Т. Какова плотность газа
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
V, л |
50 |
40 |
30 |
20 |
60 |
25 |
35 |
45 |
55 |
65 |
|
Р, мм.рт.ст |
765 |
786 |
790 |
779 |
755 |
756 |
800 |
732 |
880 |
765 |
|
Т, 0С |
18 |
25 |
20 |
8 |
30 |
45 |
13 |
10 |
12 |
15 |
|
газ |
|
|
|
|
|
|
|
|
|
|
3.
6.В сосуде находится газ. Какое давление Р он производит на
стенки сосуда, если масса газа m, его объем V, средняя квадратичная скорость
молекул ![]() .
.
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
m, г |
5 |
12 |
10 |
50 |
32 |
67 |
25 |
4 |
7 |
9 |
|
V, л |
1 |
1,5 |
2 |
2,5 |
3 |
3,5 |
4 |
4,5 |
5 |
6 |
|
|
500 |
550 |
520 |
498 |
480 |
510 |
525 |
530 |
517 |
523 |
3.7. Определите температуру Т газа, если средняя кинетическая энергия поступательного движения его молекул равна Ек
|
Вариант |
а |
б |
в |
г |
д |
|
Ек, Дж |
1,6·10-19 |
2·10-19 |
2,6·10-19 |
3·10-19 |
4·10-19 |
|
Вариант |
е |
ж |
з |
и |
к |
|
Ек, Дж |
4,5·10-19 |
6·10-19 |
7·10-19 |
8·10-19 |
9·10-19 |
3. 8.В сосуде объемом V, находится смесь m1 гелия и m2 водорода при температуре T. Определить давление и молярную массу смеси газов.
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
V, м3 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
1 |
10 |
|
m1,кг |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
12 |
10,5 |
9,5 |
|
m2, кг |
2 |
2,5 |
1,5 |
2,2 |
1,7 |
1,8 |
2,6 |
3 |
3,2 |
1,9 |
|
T, 0С |
27 |
22 |
24 |
23 |
19 |
28 |
29 |
21 |
20 |
18 |
3.9.
![]() Найти
плотность газа, если молекула за время 1 с испытывает z столкновений при
температуре Т. Какова средняя длина свободного пробега молекул?
Найти
плотность газа, если молекула за время 1 с испытывает z столкновений при
температуре Т. Какова средняя длина свободного пробега молекул?
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
d·10-10, м |
2,3 |
2,9 |
3,1 |
1,9 |
3,5 |
4 |
3,1 |
1,9 |
3,5 |
4 |
|
|
2,05 |
2 |
2,1 |
2,5 |
2,6 |
3 |
5 |
7 |
8 |
9 |
|
Т1, 0С |
12 |
15 |
7 |
28 |
25 |
10 |
35 |
50 |
40 |
55 |
|
газ |
|
|
|
|
|
|
|
|
|
|
3.10. Определить среднюю длину свободного пробега молекул и число соударений за время 1 с, происходящих между всеми молекулами газа, находящегося в сосуде емкостью V при температуре Т и давлении Р.
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
V, л |
2 |
3 |
4 |
5 |
6 |
7 |
4,5 |
2,5 |
3,5 |
4,5 |
|
Р, кПа |
100 |
93 |
74 |
42 |
52 |
45 |
13 |
35 |
49 |
60 |
|
d·10-10, м |
2,3 |
2,9 |
3,1 |
2,3 |
2,9 |
3,1 |
2,3 |
2,9 |
3,1 |
2,3 |
|
Т, 0С |
27 |
35 |
42 |
40 |
50 |
60 |
65 |
35 |
75 |
48 |
|
газ |
|
|
|
|
|
|
|
|
|
|
Номера задач, для индивидуального решения, выбираются согласно таблице вариантов (Приложение А, таблица А2).
1.Дмитриева В.Ф. Физика для профессий и специальностей технического профиля. Сборник задач: учеб.пособие для студ. учреждений сред. проф. образования / В.Ф. Дмитриева. – 4ё–е изд., стер. – М.: Издательский центр «Академия», 2014. – 256 с. 2.Дмитриева В.Ф. Физика для профессий и специальностей технического профиля. Контрольные материалы: учеб.пособие для студ. учреждений сред. проф. образования/ В.Ф.
Дмитриева, Л. И. Васильев. – 3–е изд., стер. – М.: Издательский центр «Академия», 2014. – 112 с.
Тема: Основы термодинамики
Цель: установить связь между изменением внутренней энергии системы, работой и количеством теплоты, переданной системе, сформировать понятие о первый закон термодинамики как законе сохранения энергии в тепловых процессах; развивать сравнительные, аналитические и синтетические навыки; научное мировоззрение.
Краткие теоретические сведения
Таблица 4.1 – Основные законы и формулы
|
Физические законы, переменные |
Формулы |
|
|
Внутренняя энергия U газа массой m; i – число степеней свободы; μ – молярная масса газа; R - универсальная газовая постоянная; Т - температура |
i m
2 |
|
|
Изменение внутренней энергии dU идеального газа при изменении температуры на величину dT |
i m
2 |
|
|
Элементарная работа по расширению и сжатию газа: где р – давление газа, dV – изменение объема газа. |
|
|
|
Полная работа |
A pdV V1 |
|
|
Работа газа при изотермическом расширении |
|
|
|
Работа газа при изобарном расширении |
A |
|
|
Работа газа при изохорном процессе: |
A |
|
|
Количество теплоты Q, необходимой для нагревания тела массой m; c – удельная теплоёмкость |
|
|
|
Первый закон термодинамики: где Q – количество теплоты, подводимое к системе; ΔU – изменение внутренней энергии; А – работа, совершаемая системой против внешних сил. |
Q
|
|
|
Удельная теплоемкость: |
dQ c
|
|
|
Молярная теплоемкость: 1) молярная теплоемкость изохорная; 2) молярная теплоемкость изобарная где R - универсальная газовая постоянная, i – число степеней свободы |
1)C R ; 2)CPR ; 2 |
|
|
Уравнение Майера: |
СP |
|
|
Уравнение политропы: |
|
|
|
Показатель политропы: |
n |
|
|
Работа газа при политропном процессе: |
|
|
|
Показатель адиабаты (коэффициент Пуассона): |
|
|
|
Уравнение адиабаты: |
p1V1 |
|
|
Коэффициент полезного действия η тепловой машины; Q1 – теплота, передаваемая рабочему телу нагревателем; Q2 – теплота, передаваемая рабочим телом холодильнику |
|
|
|
Коэффициент полезного действия ηк идеальной тепловой машины, работающей по циклу Карно; Т1 - температура нагревателя, и Т2 - температура холодильника |
|
k T1 |
|
Изменение энтропии при переходе из состояния 1 в состояние 2: где dQ – количество теплоты, Т – термодинамическая температура. |
S2 |
1
|
1. Внутренняя энергия некоторого количества азота при температуре 20º равна 4·103 Дж. Определить массу газа.
Дано:
μ2(N2)=24·10-3кг/моль, t = 20ºC, Т = 273+20=293 К U = 4·103 Дж.
Найти: m– ?
Решение
Внутренняя энергия газа
U ![]() RT ,
RT ,
где m – масса газа, μ – молярная масса газа, R – универсальная газовая постоянная, T – термодинамическая температура, i – число степеней свободы молекулы, так как азот двухатомный, то i=5, тогда
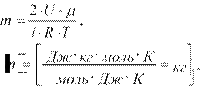
![]() 2 4 103 24 10 3 3
2 4 103 24 10 3 3
m 9,1 10 кг
5 8,31 293
Ответ: m 9,1 10 3кг .
![]() 2. Одноатомный газ был
нагрет при постоянном давлении р = 90 кПа. В результате его объем увеличился на
V = 2 см2. Найти: 1) совершенную газом работу, 2) приращение
внутренней энергии U газа, 3) количество теплоты Q, сообщенное газу. Дано:
2. Одноатомный газ был
нагрет при постоянном давлении р = 90 кПа. В результате его объем увеличился на
V = 2 см2. Найти: 1) совершенную газом работу, 2) приращение
внутренней энергии U газа, 3) количество теплоты Q, сообщенное газу. Дано:
р = 90 кПа = 90·103Па,
![]() V = 2 см3
= 2·10-6м3, p=const, i = 3.
V = 2 см3
= 2·10-6м3, p=const, i = 3.
Найти:
А – ?
![]() U– ?
U– ?
Q– ?
Решение
При изобарном процессе Р = const первый закон термодинамики можно записать в виде:

где i – показатель степени свободы молекулы, i = 3, так как гелий одноатомный газ, R – универсальная газовая постоянная, μ – молярная масса гелия. Из уравнения Менделеева – Клапейрона

3.Газ расширяясь изобарно при давлении 2.105 Па, совершает работу 200 Дж.
Определить первоначальный объем газа, если конечный объем равен 2,5 л. Дано:
р=2.105 Па, А = 200 Дж, p=const,
V2 = 2,5 л = 2,5·10-3м3. Найти: V1– ?
Решение
Работа при изобарном процессе вычисляется по формуле:
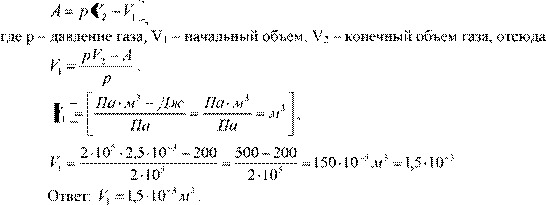 м3
м3
4. Вычислить удельные теплоемкости при постоянном объеме cv и при постоянном давлении ср неона и водорода, принимая эти газы за идеальные. Дано: i(Ne) = 3, i(H2) = 5 μ(Ne) = 20·10-3 кг/моль, μ(H2) = 2·10-3 кг/моль, Найти: cv – ?
ср – ?
Решение
Удельные теплоемкости идеальных газов выражаются
формулами cV ![]() , cP
, cP ![]() ,
,
где i – число степеней свободы молекулы газа; μ – молярная масса. Для неона (одноатомный газ) i = 3 и μ = 20·10-3 кг/моль.
Произведем вычисления:
3 8,31(Дж/ моль 2
|
К) |
||||||||
|
2 20 |
|
||||||||
|
|||||||||
![]()
![]() cv
cv ![]() 6,24 102 Дж/кг
6,24 102 Дж/кг![]() К ,
cр
К ,
cр ![]() 1,04
103 Дж/кг
1,04
103 Дж/кг![]() К .
К .
|
8,31(Дж/ моль |
К) |
|
|
2 |
|
|
|
8,31(Дж/ моль |
К) |
|
|
2 |
|
|
![]()
![]() Для водорода
(двухатомный газ) i = 5 и μ = 2·10-3 кг/моль.
Тогда: cv1,04
103 Дж/кг
К ,
Для водорода
(двухатомный газ) i = 5 и μ = 2·10-3 кг/моль.
Тогда: cv1,04
103 Дж/кг
К ,
![]() cр1,46 104 Дж/кг К .
cр1,46 104 Дж/кг К .
2
![]() Ответ:
для неона: cv 6,24 102 Дж/кг К , cр 1,04
103 Дж /кг
Ответ:
для неона: cv 6,24 102 Дж/кг К , cр 1,04
103 Дж /кг
![]() К ; для водорода:
К ; для водорода:
![]() cv 1,04 103 Дж/кг
cv 1,04 103 Дж/кг ![]() К , cр 1,46 104 Дж /кг К .
К , cр 1,46 104 Дж /кг К .
5. Кислород массой m = 2 кг занимает объем V1 = 1 м3 и находится под давлением Р1 = 0,2 МПа. Газ был нагрет сначала при постоянном давлении до объема V2 = 3 м3, а затем при постоянном объеме до давления Рз = 0,5 МПа. Найти изменение ΔU внутренней энергии газа, совершенную им работу А и теплоту Q, переданную газу. Построить график процесса.
Дано:
m = 2 кг, V1 = 1 м3, Р1 = 0,2 МПа = 0,2·106Па,
V2 = 3 м3,
Рз = 0,5 МПа = 0,5·106Па Найти:
ΔU – ?
А – ?
Q – ?
Решение
Изменение внутренней энергии газа равно:
i R
U cvm T m T ,
2
где i – число степеней свободы молекул газа (для двухатомных молекул кислорода i = 5); T T3 T1 – разность температур газа в конечном (третьем) и начальном состояниях.
![]() Начальную
и конечную температуру газа найдем из уравнения состояния идеального m газа:
PV RT , откуда
Начальную
и конечную температуру газа найдем из уравнения состояния идеального m газа:
PV RT , откуда
PV
T . mR
Работа расширения газа при постоянном давлении выражается формулой: m1 .
A1 P V R T
![]()
![]() Работа газа, нагреваемого
при постоянном объеме, равна нулю: A20.
Следовательно, полная работа, совершаемая газом, A A1 A2 A1. Согласно первому началу
термодинамики, количество теплоты Q, переданное газу, равна сумме
изменения внутренней энергии ΔU и работы А:
Работа газа, нагреваемого
при постоянном объеме, равна нулю: A20.
Следовательно, полная работа, совершаемая газом, A A1 A2 A1. Согласно первому началу
термодинамики, количество теплоты Q, переданное газу, равна сумме
изменения внутренней энергии ΔU и работы А:
Q U A.
Произведем вычисления, учтя, что для кислорода μ = 32·10-3 кг/моль:
2 105Па 1м3 0,032кг / моль
Т1 385К ,
2кг 8,31Дж / моль К
2 105Па 3м3 0,032кг / моль
Т2 1155К ,
2кг 8,31Дж / моль К
5 105Па 3м3 0,032кмоль/ К
Т3 2887К .
2кг 8,31Дж/ моль К
![]() 8,31(Дж
/ моль К) 2кг (1155К 385К) 60,4МДж,
8,31(Дж
/ моль К) 2кг (1155К 385К) 60,4МДж,
А А1 0,4 10 Дж
0,032кг / моль
U
![]()
![]() 5 8,31(Дж/ моль
К) 2кг (2887К 385К) 3,24 106 Дж3,24МДж,
5 8,31(Дж/ моль
К) 2кг (2887К 385К) 3,24 106 Дж3,24МДж,
2 0,032кг/ моль
Q U A 0,4 106 Дж 3,24 106 Дж 3,64 106 Дж 3,64МДж.
Ответ: U 3,24МДж, А 0,4МДж, Q 3,64МДж.
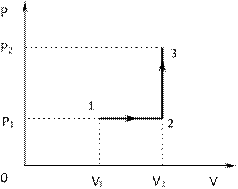
График термодинамического процесса 6. В цилиндре под поршнем находится водород массой m = 0,02 кг при температуре Т1 = 300 К. Водород сначала расширился адиабатно, увеличив свой объем в n1 = 5 раз, а затем был сжат изотермически, причем объем газа уменьшился в n2 = 5 раз. Найти температуру в конце адиабатного расширения и работу, совершаемую газом при этих процессах. Изобразить процесс графически. Дано:
m = 0,02 кг, Т1 = 300 К, n1 = 5 раз, n2 = 5 раз.
Найти:
Т2 – ?
А1 – ?
А2 – ? Решение
Температуры и объемы газа, совершающего адиабатный процесс, связаны между собой соотношением:
1
T2 V1 или ,
![]() T1 V1 1 1
T1 V1 1 1
![]() где γ –
отношение теплоемкостей газа при постоянном давлении и постоянном объеме; n1 V2 V1 . Отсюда
получаем следующее выражение для конечной температуры: T2 T1 n1 1 .
где γ –
отношение теплоемкостей газа при постоянном давлении и постоянном объеме; n1 V2 V1 . Отсюда
получаем следующее выражение для конечной температуры: T2 T1 n1 1 .
Работа А1 газа при адиабатном расширении может быть определена по формуле: m m i
A1 CV T1 T2 R T1 T2 ,
2
где Cv – молярная теплоемкость газа при постоянном объеме. Работа А2 газа при изотермическом процессе может быть выражена в виде:
![]()
![]() V1 или A2 mRT2 ln 1 , RT2 ln
V1 или A2 mRT2 ln 1 , RT2 ln
V2 n2
где n2
Найдем числовые значения искомых величин, учитывая, что для водорода как двухатомного газа γ = 1,4, i = 5 и μ = 2·10-3 кг/моль:
300K 300K 300K
![]() T2 51,4 1 50,4 1,91 157K
.
T2 51,4 1 50,4 1,91 157K
.
![]()
![]() A1 0,02кг 5
8,31Дж / моль К 300К 157К 29,8 103 Дж29,8кДж ,
A1 0,02кг 5
8,31Дж / моль К 300К 157К 29,8 103 Дж29,8кДж ,
|
2 |
|
2 |
|
|
0,02кг |
5 |
8,31Дж / моль |
|
![]()
![]() A2 2
10 3кг / моль К
157К ln 15 21 103 Дж21кДж .
A2 2
10 3кг / моль К
157К ln 15 21 103 Дж21кДж .
Знак «минус» показывает, что при сжатии работа газа совершается над газом внешними силами.
График процесса приведен на рисунке
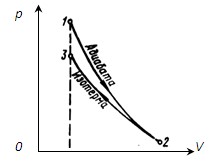
![]()
![]() Ответ:
T2157K , A1 29,8кДж , A2 21кДж
Ответ:
T2157K , A1 29,8кДж , A2 21кДж
7. 10 г кислорода находятся под давлением 3 бар при температуре 10о С. После нагревания при постоянном давлении газ занял объем 10 л. Найти: 1) количество тепла, полученного газом; 2) энергию теплового движения газа до и после нагревания.
Дано:
m=10г =10-2кг, р=3 бар =3·105Па, V =10 л = 10-2м3. Найти: ΔQ – ?
W1 – ?
W2 – ?
Решение
1 Количество тепла, полученного газом, найдем по формуле:
![]()
m
Чтобы Т2, запишем уравнение состояния газа до нагревания: pV1 RT1 и после
![]()
![]() mV2 , где V1 mRT1 . нагревания: pV2 RT2 . Из этих уравнений
получаем: T21
mV2 , где V1 mRT1 . нагревания: pV2 RT2 . Из этих уравнений
получаем: T21
V1 p
Следовательно,
![]() T2 mRV2p 0,03210кг/моль10
3кг 810,3110Дж3м/ моль3 3 10К5Па 1155К .
T2 mRV2p 0,03210кг/моль10
3кг 810,3110Дж3м/ моль3 3 10К5Па 1155К .
Таким образом, (T2 T1) 1155K 283K 873K ,
![]() Q m
i 2 R(T2 T1) 10 10 3кг 5 2 8,31Дж /
моль К 873К 7,9 103 Дж .
Q m
i 2 R(T2 T1) 10 10 3кг 5 2 8,31Дж /
моль К 873К 7,9 103 Дж .
2 0,032кг / моль 2
2 Энергия газа до нагревания может быть найдена по формуле:
![]() W1 m i RT1 10
10 3кг 5
8,31Дж / моль К 283К 1,8 103 Дж.
W1 m i RT1 10
10 3кг 5
8,31Дж / моль К 283К 1,8 103 Дж.
2 0,032кг / моль 2
Энергия газа после нагревания:
![]()
![]()
![]() m i 10 10 3кг 53 .
W2 RT2 8,31Дж /
моль К 1155К 7,6 10 Дж
m i 10 10 3кг 53 .
W2 RT2 8,31Дж /
моль К 1155К 7,6 10 Дж
2 0,032кг / моль 2
![]() Ответ: Q 7,9
103 Дж ,
W1 1,8
103 Дж ,
W2 7,6
103 Дж .
Ответ: Q 7,9
103 Дж ,
W1 1,8
103 Дж ,
W2 7,6
103 Дж .
8. В закрытом сосуде объемом 10 л находится воздух при давлении 105 Па. Какое 5 Па? количество тепла надо сообщить воздуху, чтобы повысит давление до 5·10 Дано: V = 10л =10-2м3, р1 = 105Па, р2 = 5·105Па.
Найти: Q – ?
Решение
![]()
![]() Количество теплоты, которое необходимо сообщить воздуху,
находится по формуле:
Количество теплоты, которое необходимо сообщить воздуху,
находится по формуле:
i
![]()
![]() Теплоемкость воздуха при
постоянном объеме определяется формулой: CVR , где 2 i5
- число степеней свободы для двухатомного газа (воздух принимается за
двухатомный
Теплоемкость воздуха при
постоянном объеме определяется формулой: CVR , где 2 i5
- число степеней свободы для двухатомного газа (воздух принимается за
двухатомный
газ). Подставляя два последних уравнения в первую формулу, получим:
Q
![]()
![]()
![]() Q (5
105Па 1
105Па) 1
104 Дж .
Q (5
105Па 1
105Па) 1
104 Дж .
Ответ: Q
9. Какой должна быть температура нагревателя, для того чтобы в принципе стало возможным достижение значения КПД тепловой машины 80%, если температура
0 холодильника 27 С?
Дано:
η=80%,
Т2 = 270С.
Найти: Т1 – ?
Решение
КПД идеальной тепловой машины:
![]() 100%, (1)
100%, (1)
Т1
где Т1 – температура нагревателя, Т2 – температура холодильника. Преобразуем выражение (1)
![]() Т1 Т1 Т2 ., Т2 Т1 Т1,
Т1 Т1 Т2 ., Т2 Т1 Т1,
Т2 Т1 1 ,
Т2 ,
Т1
1
Т2 = 27+273=300К,
300K
![]() Т11500К .
Т11500К .
1 0,8
Ответ: Т1 1500К .
10.Идеальная тепловая машина работает по циклу Карно. Определить к.п.д. цикла, если известно, что за один цикл была произведена работа, равная 3000 Дж, и 4 Дж теплоты. холодильнику было передано 1,35·10 Дано:
А = 3000 Дж,
Q2 = 1,35·104 Дж. Найти: η – ?
Решение
КПД тепловой машины
![]() 100%
100%
Q1 , (1)
где А – совершаемая работа, Q1 – количество теплоты полученное от нагревателя. Работа равна:
![]() 2
2
тогда
18%.
11. В процессе работы тепловой машины за некоторое время рабочим телом было получено от нагревателя количество теплоты Q1=1,5·106Дж, передано холодильнику Q2=-
6
1,2·10 Дж. Вычислите КПД машины и сравните его с максимально возможным КПД
0 машины, если температура нагревателя и холодильника соответственно равны 250 С и 300С. Дано: Q1=1,5·106Дж,
Q2=-1,2·106Дж, Т1 = 2500С, Т2= 300С.
Найти: η1 – ?
η2 – ?
Решение
КПД тепловой машины
![]() 100%
100%
Q1 ,
где Q1 – количество теплоты, полученное от нагревателя, Q2 – количество теплоты, преданное холодильнику,
1,5 106 Дж 1,2 106 Дж
1
![]() 1,5
106 Дж 100% 20%
1,5
106 Дж 100% 20%
КПД идеальной тепловой машины:
2 T1 T2 100%,
Т1
где Т1 – температура нагревателя, Т2 – температура холодильника.
Т1 = 250+273=523К, Т2 = 30+273=303К, тогда
523К 303К
![]() 2 100% 42%.
2 100% 42%.
523К
Ответ: 1 20%, 2 42%
1.Найти внутреннюю энергию двухатомного газа, находящегося в сосуде объемом 2 л под давлением 150 кПа. (Ответ: 750 Дж)
2. Найти удельную теплоемкость кислорода: 1) при V= const и 2) при р = const.(Ответ: сv=650 Дж/кг·К; ср=910 Дж/кг·К)
3. Какое количество теплоты надо сообщить массе 12 г кислорода, чтобы нагреть его на 500С при постоянном давлении.(Ответ: 545 Дж)
4. В сосуде объемом 5 л находится газ при давлении 200 кПа и температуре 170С. при изобарическом расширен газа была совершена работа 196 Дж. На сколько нагрели газ? (Ответ:
57 К)
5.Количество 1 кмоль многоатомного газа нагревается на 100 К в условиях свободного расширении. Найти количество теплоты, сообщаемое газу, изменение его внутренней энергии и работу А расширения газа.(Ответ: А= 831 кДж; ΔU= 2,49 МДж; Q=3,32 МДж).
6.Масса 10,5 г азота изотермически расширяется при температуре -230С, причем его давление изменится от 250 кПа до 100 кПа. найти работу А, совершенную газом при расширении. (Ответ: 713,85 Дж)
7. Найти изменение энтропии при плавлении массы 1 кг льда (температура льда 00С)
(Ответ: 1209 Дж/кг)
8.Масса 10,5 г азота изотермически расширяется от объема 2 л до объема 5 л. Найти изменение энтропии при этом процессе.(Ответ: 2,85 Дж/К)
9. Температура нагревателя тепловой машины 500 К. Температура холодильника 400 К. Определить КПД тепловой машины, работающей по циклу Карно, и полезную мощность машины, если нагреватель ежесекундно передает ей 1675 Дж теплоты. (Ответ: 335 Дж, 335 Вт)
10. Тепловая машина работает по циклу Карно. Определить работу тепловой машины за один цикл, если она в течении цикла получает от нагревателя количество теплоты Q1=2085 Дж. Температура нагревателя Т1=500 К, температура холодильника Т2=300 К.
1. Дайте определение внутренней энергии. Из чего состоит внутренняя энергия газа?
2. Как может быть изменена внутренняя энергия?
3. Как зависит сила взаимодействия между молекулами от расстояния?
4. Какими уравнениями определяется внутренняя энергия и ее изменение?
5. Что характеризует число степеней свободы?
6. Как определяется работа в термодинамике?
7. Какой физический процесс называется теплопередачей? Какие способы теплопередачи Вы знаете?
8. Какую физическую величину называют количеством теплоты? В каких единицах измеряется количество теплоты?
9. Какую физическую величину называют энтропией? В каких единицах измеряется энтропия?
10. Сформулируйте первый закон термодинамики. Какой фундаментальный смысл несет этот закон?
11. Как первый закон термодинамики формулируется для различных изопроцессов?
12. Какой изопроцесс называется адиабатным?
13. От чего зависит КПД тепловой машины?
14. Сформулируйте второе начало термодинамики.
15. Приведите примеры известных вам тепловых двигателей.
4.1.Какова внутренняя энергия газа, заполняющего аэростат объемом Vпри давлении Р?
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
V, м3 |
10 |
20 |
30 |
15 |
35 |
40 |
50 |
25 |
60 |
55 |
|
Р, кПа |
30 |
15 |
20 |
25 |
40 |
35 |
40 |
45 |
50 |
60 |
|
|
|
|
|
|
|
|
|
|
|
|
4. 2.Какую работу совершает идеальный газ количеством вещества ν при его изобарном нагревании на ΔТ?
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
ν, кмоль |
1 |
5 |
2 |
3,5 |
4 |
5,5 |
7,5 |
12 |
11 |
9 |
|
ΔТ, К |
3 |
7 |
5 |
6 |
8 |
9 |
12 |
10 |
13 |
11 |
4.3. Определите удельные теплоемкости cv и ср смеси газов, содержащей газ массой m1 и газ массой m2
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
m1, г |
1 |
2 |
3 |
1,5 |
3,5 |
4 |
5 |
2,5 |
6 |
5,5 |
|
m2, г |
3 |
1,5 |
2 |
2,5 |
4 |
3,5 |
4 |
4,5 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4.4. В закрытом сосуде объемом V находится воздух при давлении P1. Какое количество тепла надо сообщить воздуху, чтобы повысит давление до P2.
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
V, м3 |
10 |
20 |
30 |
15 |
35 |
40 |
50 |
25 |
60 |
55 |
|
Р1, кПа |
300 |
150 |
200 |
250 |
400 |
350 |
400 |
450 |
500 |
600 |
|
Р2, кПа |
500 |
300 |
350 |
500 |
600 |
550 |
700 |
650 |
800 |
850 |
4.5. Количество ν многоатомного газа нагревается на ΔТ в условиях свободного расширении. Найти количество теплоты, сообщаемое газу, изменение его внутренней энергии и работу А расширения газа

4.6.Под давлением р при температуре Т находятся V воздуха. Какая работа будет совершена при его изобарном нагревании на ΔT?
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
р, кПа |
10 |
12 |
14 |
15 |
17 |
19 |
20 |
22 |
24 |
25 |
|
Т, К |
273 |
300 |
280 |
290 |
310 |
320 |
295 |
305 |
296 |
312 |
|
V, м3 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
ΔТ, К |
10 |
12 |
14 |
15 |
17 |
20 |
22 |
25 |
27 |
30 |
4.7.В цилиндре под поршнем находится азот массой m. Газ был нагрет от температуры t1 до температуры t2 при постоянном давлении. Определить теплоту Q, переданную газу, совершаемую работу А и приращение ΔU внутренней энергии.
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
m,г |
10 |
12 |
14 |
15 |
17 |
19 |
20 |
22 |
24 |
25 |
|
t1,0С |
20 |
30 |
40 |
50 |
60 |
70 |
15 |
25 |
35 |
45 |
|
t2, 0С |
180 |
185 |
190 |
195 |
200 |
150 |
225 |
210 |
300 |
175 |
4.8.Найти изменение энтропии при изотермическом расширении массы m водорода от давления Р1 до давления Р2.
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
m,г |
10 |
12 |
14 |
15 |
17 |
19 |
20 |
22 |
24 |
25 |
|
Р1, кПа |
200 |
300 |
400 |
500 |
600 |
700 |
150 |
250 |
350 |
450 |
|
Р2, кПа |
100 |
150 |
200 |
250 |
300 |
350 |
75 |
125 |
175 |
225 |
4. 9.Совершая цикл Карно, газ отдал охладителю теплоту Q1. Работа цикла А. Определить температуру нагревателя, если температура охладителя t.
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
Q1, кДж |
1 |
1,2 |
1,4 |
1,5 |
1,7 |
1,9 |
2 |
2,2 |
2,4 |
2,5 |
|
А, кДж |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
1,5 |
1,1 |
|
t,0С |
27 |
27,5 |
28 |
28,5 |
29 |
29,5 |
30 |
30,5 |
31 |
31,5 |
4.10. Газ, совершающий цикл Карно, отдал теплоприемнику 65% теплоты, полученной от теплоотдатчика. Определить температуру T2 теплоприемника, если температура теплоотдатчика T1.
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
Т1, К |
400 |
420 |
430 |
450 |
500 |
520 |
540 |
550 |
570 |
600 |
Номера задач, для индивидуального решения, выбираются согласно таблице вариантов
(Приложение А, таблица А2).
1.Дмитриева В.Ф. Физика для профессий и специальностей технического профиля. Сборник задач: учеб.пособие для студ. учреждений сред. проф. образования / В.Ф. Дмитриева. – 4ё–е изд., стер. – М.: Издательский центр «Академия», 2014. – 256 с. 2.Дмитриева В.Ф. Физика для профессий и специальностей технического профиля. Контрольные материалы: учеб.пособие для студ. учреждений сред. проф. образования/ В.Ф.
Дмитриева, Л. И. Васильев. – 3–е изд., стер. – М.:
Издательский центр «Академия», 2014. – 112 с.
Тема: Электростатика. Постоянный электрический ток
Цель: обобщение и углубление знаний курсантов об электрическом поле и токе, о направлении и условиях существования тока, о действиях тока, о силе тока, об электрическом напряжении, сопротивлении, удельном сопротивлении, о законе Ома; развитие интеллектуальных умений: аналитических, проектировочных, конструктивных; воспитание профессионально значимых качеств: самостоятельности, ответственности, точности, творческой инициативы.
Краткие теоретические сведения
Таблица 5.1 – Основные законы и формулы
|
Физические законы, переменные |
Формулы |
|
Закон сохранения электрического заряда q: q1,q2,qn – заряды частиц. |
|
|
Закон Кулона:
|
FK |
|
r Напряжённость E электростатического поля: r где F – сила, с которой поле действует на точечный заряд |
|
|
Напряжённость электрического поля точечного заряда: |
E |
|
Связь между векторами электрической индукции и напряжённости электрического поля: |
|
|
Принцип суперпозиции напряжённостей электрических полей: |
|
|
Потенциал электростатического поля: |
q0 |
|
Потенциал поля точечного заряда: |
|
|
Работа сил электрического поля по перемещению заряда q из точки с потенциалом φ1 в точку с потенциалом φ2: |
|
|
Связь между напряжённостью и потенциалом неоднородного и однородного полей: |
E
|
|
Электроёмкость уединённого проводника: |
C |
|
Электроёмкость сферы: |
C |
|
Электроёмкость плоского конденсатора: |
C
|
|
Электроёмкость последовательно соединённых конденсаторов: |
|
||
|
Электроёмкость параллельно соединённых конденсаторов: |
|
||
|
Энергия заряженного конденсатора: |
1
2 |
||
|
Объёмная плотность энергии электрического поля: |
wE 2 |
||
|
Сила тока:
|
|
dq
dt |
|
|
Плотность тока:
1 n 3 ; j А2 ; e 1,6 10 19Кл м м |
|
j |
|
|
Сопротивление проводника: где ρ – удельное сопротивление проводника; l – длина проводника; S – площадь поперечного сечения проводника.
|
|
R S |
|
|
Электродвижущая сила (ЭДС): где Аст – работа сторонних сил, при перемещении единичного положительного заряда q.
|
|
q |
|
|
Закон Ома: 1) для однородного участка цепи: 2) в дифференциальной форме: где j – плотность тока, E – напряженность электрического поля; ρ–удельное сопротивление проводника 3) для участка цепи, содержащего ЭДС: где ε – электродвижущая сила источника тока; R – внешнее сопротивление; r – внутреннее сопротивление; 4) для замкнутой цепи: |
3) I |
|
|
|
Последовательное соединение проводников: где n–
число проводников, алгебраическая
сумма напряжений, на каждом проводнике, |
I1 |
U R |
|
|
Параллельное соединение проводников: где n– число проводников,
|
|
||
|
алгебраическая сумма сил токов, на каждом проводнике. |
|
||
|
Температурная зависимость сопротивления: где ρ и ρ0, R иR0 – соответственно удельные сопротивления и сопротивления проводника при температуре t и 00С 9шкала Цельсия), α – температурный коэффициент сопротивления |
|
|
|
|
Работа тока: где I– сила тока, U– напряжение, Δt – интервал времени.
|
A |
|
|
|
Мощность тока:
|
|
||
|
Закон Джоуля – Ленца: где Q – количество теплоты, выделившейся в проводнике за время t при прохождении тока, I – сила тока в проводнике, R – сопротивление проводника.
|
|
||
|
Законы Кирхгофа для разветвлённых цепей: 1) Первый закон Кирхгофа: алгебраическая сумма токов, сходящихся в узле, равна нулю: 2) Второй закон Кирхгофа: в любом замкнутом контуре, произвольно выбранном в разветвленной электрической цепи, алгебраическая сумма произведений сил токов Iiна сопротивление Ri соответствующих участков этого контура равна алгебраической сумме ЭДС εn, встречающихся в этом контуре: |
1)
2) |
||
1. Перед составлением уравнений необходимо произвольно выбрать: а) направление токов на всех участках цепи и указать их стрелками на чертеже; б) направление обхода контуров.
2. При составлении уравнений по первому закону Кирхгофа надо считать токи, подходящие к узлу, положительными, отходящие от узла, - отрицательными. Число уравнений, составляемых по первому закону Кирхгофа, должно быть на единицу меньше числа узлов, содержащихся в цепи.
3.При составлении уравнений по второму закону Кирхгофа необходимо соблюдать правило знаков: а) если ток по направлению совпадает с выбранным направлением обхода контура, то соответствующее падение напряжения IR входит в уравнение со знаком плюс. В противном случае произведение IR берется со знаком минус; 3) ЭДС входит в уравнение со знаком плюс, если оно повышает потенциал в направлении обхода контура, т.е двигаясь по контуру, сначала встречаем отрицательный полюс источника тока, затем положительный, в противном случае ЭДС берется со знаком минус.
4. Чтобы все уравнения, составленные на основании второго закона Кирхгофа, были независимыми, необходимо каждый раз рассматривать контуры, содержащие хотя бы одну ветвь, не входящую в уже использованные контуры.
5. Общее число независимых уравнений, составленных по первому и второму закону Кирхгофа, должно быть равно числу токов, текущих в контуре.
6. Для упрощения выкладок, связанных с решением системы уравнений, необходимо предварительно подставить числовые значения всех известных величин.
Если при решении уравнений получены отрицательные значения силы тока или сопротивления, то это означает, что, в действительности, ток через данное сопротивление течет в направлении, противоположном произвольно выбранному.
1.Определите силу взаимодействия электрона с ядром в атоме водорода, если
-8 расстояние между ними равно 0,5·10 см. Дано: r = 0,5·10-8см = 0,5·10-10м, q1 = –1,6·10-19 Кл , q2 = 1,6·10-19 Кл. Найти: F– ? Решение
В ядре атома водорода находится протон, поэтому взаимодействие электрона и протона можно рассматривать, как взаимодействие двух точечных зарядов.
Сила взаимодействия между двумя точечными зарядами определяется по закону Кулона
 Н .
Н .
![]() 2. Во сколько раз кулоновская
сила взаимодействия электрона с ядром в атоме водорода больше силы их
гравитационного взаимодействия? Масса электрона me 9,11 10 31кг , а масса протона mР 1,67 10 27кг.
Гравитационная постоянная
2. Во сколько раз кулоновская
сила взаимодействия электрона с ядром в атоме водорода больше силы их
гравитационного взаимодействия? Масса электрона me 9,11 10 31кг , а масса протона mР 1,67 10 27кг.
Гравитационная постоянная
2
G 6,67 10 11 Н м2
кг Дано:
![]() me 9,11 10 31кг , mР 1,67 10 27кг,
me 9,11 10 31кг , mР 1,67 10 27кг,
G 6,67 10 11 Н м2 2
кг ,
qе = –1,6·10-19 Кл , qр = 1,6·10-19 Кл.
Найти:
Fк
![]()
F гр – ?
Решение
В ядре атома водорода находится протон, поэтому взаимодействие электрона и протона можно рассматривать, как взаимодействие двух точечных зарядов.
Сила взаимодействия между двумя точечными зарядами определяется по закону Кулона:

Гравитационная сила взаимодействия между частицами
![]()
![]() масса протона.G 6,67
10 11 Н м2 2 гдеme кг–
масса протона.G 6,67
10 11 Н м2 2 гдеme кг–
кг
39.
3.Два одинаковых маленьких шарика подвешены на невесомых нитях длиной l =
12 см каждая в одной точке. Когда им сообщили одинаковые заряды Q = 4 нКл, шарики
0 разошлись на угол α = 20 . Найти силу натяжения каждой нити, если между шариками находится некоторая среда ε = 7,8.
Дано:
l = 12 см = 0,12 м, Q = 4 нКл = 4·10-9 Кл,
α = 200, ε = 7,8.
Найти:
![]()
Т - ?
Решение
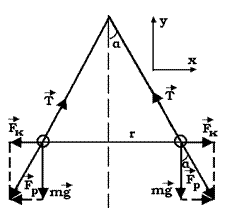
Сделаем чертеж к задаче. На каждый из отклоненных шариков действуют силы: сила
r r
тяжести - mg , сила натяжения нитиT и сила взаимодействия (отталкивания) шариков, то есть
r
сила Кулона Fk .
Так как модули сил, действующие на шарики, одинаковы, то более подробно можно рассматривать только один из шариков, например правый (см рис).
![]()
![]() Шарики находятся в
равновесии под действием приложенных сил, поэтому согласно первому закону
Ньютона, запишем это условие равновесия: R0
- результирующая сила, или m
Шарики находятся в
равновесии под действием приложенных сил, поэтому согласно первому закону
Ньютона, запишем это условие равновесия: R0
- результирующая сила, или mg
T Fк 0. (1)
Выберем прямоугольную систему координат, связанную с одним из шариков, и перепишем это уравнение проекциях на оси координат.
Проекции сил на оси
![]() (2)
(2)
(3)
F (4)
0 постоянная,
sin
отсюда
r (5)
отсюда
T
T H
![]() Ответ:
T 8 10 6 Н.
Ответ:
T 8 10 6 Н.
4.Найти напряженность электрического поля в точке, лежащей посередине между точечными зарядами q1=18·10-9 Кл и q2=16·10-9 Кл. Расстояние между зарядами равно r =
0,2 м.
Дано:
q1=18·10-9 Кл, q2=16·10-9 Кл, r = 0,2 м.
Найти: Е – ?
Решение
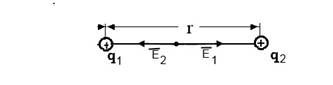
Для решения задачи воспользуемся формулой напряженности поля точечного заряда
Е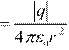 (где ε0
– электрическая постоянная) и принципом суперпозиции, в соответствии с
(где ε0
– электрическая постоянная) и принципом суперпозиции, в соответствии с
которым, напряженность поля, созданного в данной точке несколькими точечными зарядами, является векторной суммой напряженностей, создаваемых каждым зарядом в отдельности.
![]()
Каждый из зарядов q1 и q2 создает в указанной точке поля с напряженностями Е1и Е2 соответственно. Векторы напряженности изображены на рисунке
![]()
Поскольку векторы напряженности Е1и Е2 направлены в разные стороны, величина напряженности результирующего поля равна
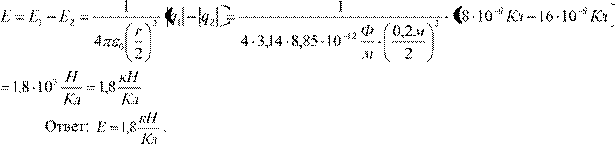
5. Какую работу совершают силы электрического поля, если одноименные заряды 1 и 2 нКл, находившиеся на расстоянии 1 см, разошлись на расстояние 10 см? Дано:
q1 = 1 нКл= 10-9Кл, q2 = 2 нКл =2·10-9Кл, r1 = 1 см= 10-2м, r2 = 10 см = 0,1 м Найти: А – ? Решение
Удобно считать один из шариков неподвижным, образующим электрическое поле, а другой движущимся в поле первого шарика.
Пусть заряд q1 шарика создает поле, тогда шарик с зарядом q2 движется в этом поле из точки, находящейся на расстоянии r1 от шарика q1, в точку, находящуюся на расстоянии r2 от него.
Работа, совершаемая внешней силой:
А ![]() q ,
q ,
где φ1 и φ2 – потенциалы начальной и конечной точек поля. Поле образовано точечными зарядами, поэтому:
где k 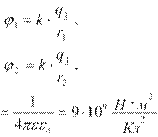 , так как ε = 1 –
диэлектрическая проницаемость среды, ε0 =
, так как ε = 1 –
диэлектрическая проницаемость среды, ε0 =
8,85·10-12Кл2/Н·м2 – электрическая постоянная.
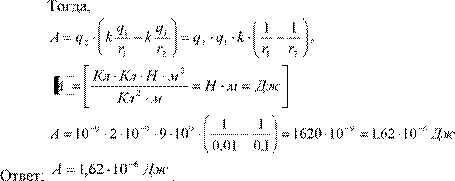
6. Площадь пластин воздушного конденсатора S = 100 см2, расстояние между пластинами d = 5 мм. К пластинам приложена разность потенциалов U = 600 В. После отключения питания конденсатор погружают в керосин. Какой стала разность потенциалов между пластинами?
Дано:
S = 100 см2 = 100·10-4м2, d = 5 мм = 5·10-3м, U1 = 600 В, εк = 2,1.
Найти: U2 – ?
Решение
Емкость плоского конденсатора
С
![]() , (1)
, (1)
d
где ε0 – электрическая постоянная, ε – диэлектрическая проницаемость среды. С другой стороны, емкость конденсатора, по определению q
![]() С.
(2)
С.
(2)
U
Заряд q на обкладках после отключения от источника и погружении конденсатора в керосин не изменится, т.е
q1 q2, (3)
![]() Тогда
из формулы (2) получим C1U1 C2U2, Отсюда,
Тогда
из формулы (2) получим C1U1 C2U2, Отсюда,
C1U1 ,
U2
C2
С учетом (1)
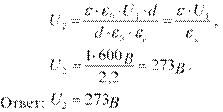
7. Энергия плоского воздушного конденсатора 0,4 нДж, разность потенциалов на обкладках 600 В, площадь пластин 1 см2. Определить расстояние между обкладками, напряженность и объемную плотность энергии поля конденсатора. Дано:
W=0,4 нДж=0,4·10-9Дж,
U=600 В,
S=1 см2=10-4м2 Найти:
d=? E=? w=?
Решение:
Энергия плоского конденсатора
CU 2
![]() W
W
2
Емкость плоского конденсатора
0S ,
С
d
где ε0 – электрическая постоянная, ε – диэлектрическая проницаемость среды. Тогда
![]() d
d
d E
w
w
8.Найти падение напряжения в проводнике, если за время t= 1 мин по нему прошел электрический заряд, равный Q= 80 Кл, а его сопротивление R=1,5Ом. Дано:
t= 1 мин=60с, Q= 80 Кл, R=1,5 Ом.
Найти: U=?
Решение:
По закону Ома для однородного участка цепи:
![]() I
I
U
Ответ: U=2В
9. Плотность тока в никелиновом проводнике длиной 25 м равна 1 МА/м2.
Определить разность потенциалов на концах проводника. Дано:
l=25 м j=1 МА/м2=106 А/м2 Найти: U=?
Решение:
Плотность тока по определению
I
![]() j
j
S
где I - сила тока, S площадь сечение проводника. По закону Ома
![]()
где R - электрическое сопротивление, ρ=0,4·10-6 Ом·м – удельное сопротивление S
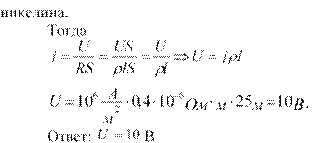
10. На баллоне электрической лампы написано 220 В, 100 Вт. Для измерения сопротивления нити накала в холодном состоянии на лампу подали напряжение U = 2 В, при этом сила тока была I = 54 мА. Найти температуру накала T вольфрамовой нити. Дано:
U1 = 220 В,
U2 = 100 Вт, U = 2 В,
I = 54 мА =54·10-3А.
Найти:
T=?
Решение:
Зависимость сопротивления от температуры
![]()
R2
где α=0,0048К-1 температурный коэффициент сопротивления. Мощность лампы
![]() P1 U12 R1 U12 48400В2 484Ом.
P1 U12 R1 U12 48400В2 484Ом.
R1 P1 100Вт
По закону Ома
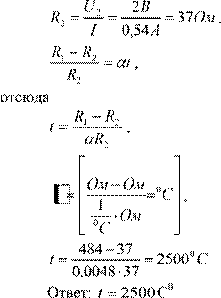
11.Две группы из трех последовательно соединенных элементов соединены параллельно. ЭДС ε каждого элемента равна 1,2В, внутреннее сопротивление r=0,2Ом. Полученная батарея замкнута на внешнее сопротивление R=1,5 Ом. Найти силу тока I во внешней цепи.
Дано:
ε = 1,2В, r=0,2Ом, R=1,5 Ом, n=3, m=2
Найти: I =?
Решение:
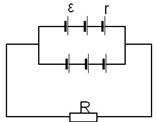
Закон Ома для замкнутой цепи:
I ![]() ,
,
где I – сила тока,ε – электродвижущая сила, R – внешнее сопротивление, r – внутреннее сопротивление

12. Определить число электронов, проходящих в секунду через единицу площади поперечного сечения железной проволоки длиной 20 м при напряжении на ее концах 16В. Дано: S=1м2, t=1c,
l=20 м, U=16В, ρ=9,8·10-8Ом·м Найти: N=?
Решение:
Число электронов q
![]() n e
n e
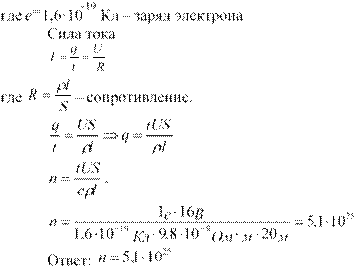
13. Найти токи I, в отдельных ветвях мостика Уитстона при условии, что через гальванометр идет ток IГ = 0. ЭДС элемента ε = 2 В, сопротивления R1 = 30 Ом, R2 = 45 Ом и R3 = 200 Ом Дано:
IГ = 0,
ε = 2 В,
R1 = 30 Ом,
R2 = 45 Ом, R3 = 200 Ом
Найти:
I1– ?
I2– ?
I3– ?
I4– ?
![]() Решение
Решение
Рисунок 5.4 Рисунок 5.5
Для решения задачи воспользуемся законами Кирхгофа.
Сначала необходимо выбрать (произвольно) направления токов в ветвях. Если мы ошиблись в выборе направления какого–нибудь тока, то в окончательном решении этот ток получится отрицательным, если же случайно выбрано правильное направление тока, то он получится положительным.
Так как IГ = 0, то потенциалы в точках 1 и 2 одинаковые, следовательно, можно рассматривать упрощенную эквивалентную схему (рис 20) По первому закону Кирхгофа для узла 1 имеем:
I
![]() I3 (1)
I3 (1)
Применим второй закон Кирхгофа для контуров KLBCMN и KLADMN запишем:
![]() (2)
(2)
(3)
Поскольку UAD=UВС, а также I1=I2, I3 = I4, то падения потенциалов на сопротивлениях R2и R4 равны между собой, то
I1R2 = I3R4 (4)
![]()
![]() Из уравнения (2) находим, что
Из уравнения (2) находим, что
Из уравнения (4) находим, что
![]() I1R2 (7)
I1R2 (7)
R4
I3
Подставляя (5) в (7), получаем
R2 (8)
R4
I3 R1 R2
Решая совместно уравнения (6) и (8) и учитывая, что I3 = I4, окончательно получаем
R1 (9)
I3 I4
R3 R1 R2
Вычислим:
|
30Ом |
2В |
|
|
200Ом |
|
|
![]()
![]()
![]() I3 I40,004А4мА.
I3 I40,004А4мА.
Ответ:
I1 I2 26,7мА, I3 ![]() 4мА.
4мА.
14.ЭДС элементов ε1 =2,1 В и ε2 = 1,9 В, сопротивления R1 = 45 Ом, R2 = 10 Ом, R3 = 10 Ом. Найти токи I во всех участках цепи. Дано: ε1 =2,1 В, ε2 = 1,9 В, R1 = 45 Ом,
R2 = 10 Ом, R3 = 10 Ом.
Найти:
I1– ?
I2– ?
I3– ?
Решение
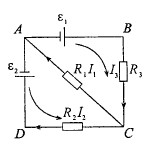
На рисунке стрелками указано выбранное направление токов. Для узла А согласно первому закону Кирхгофа запишем:
I1 ![]() I3. для контуров АВС и
ACD по второму правилу Кирхгофа имеем:
I3. для контуров АВС и
ACD по второму правилу Кирхгофа имеем:
![]() I3R3,
I3R3,
I1R1.
![]() Подставляя числовые данные,
получим систему уравнений: I3 I1 I2,
Подставляя числовые данные,
получим систему уравнений: I3 I1 I2,
10I3 45I1 2,1,
45I1 10I2 1,9
![]() Решая
эту систему, получим: I1 0,04A,
Решая
эту систему, получим: I1 0,04A,
I2 0,01A,
![]() I30,03A.
I30,03A.
![]()
![]()
![]() Знак «-» у тока I2
указывает на то, что его направление противоположно выбранному. Ответ: I10,04A, I2 0,01A,
I30,03A.
Знак «-» у тока I2
указывает на то, что его направление противоположно выбранному. Ответ: I10,04A, I2 0,01A,
I30,03A.
15. Два элемента с одинаковыми ε1 =ε2 =2 В и внутренними сопротивлениями r1= 1 Ом и r2 = 2 Ом замкнуты на внешнее сопротивление R. Через элемент ЭДС ε1 течет ток I1 = 1 А. Найти сопротивление R и ток I2, текущий через элемент с ЭДС ε2. какой ток I течет через сопротивление R?
Дано: ε1 =ε2 =2 В, r1= 1 Ом, r2 = 2 Ом, I1 = 1 А.
Найти:
I2– ? R– ? I– ?
Решение
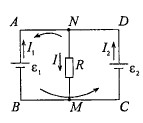
Выберем и рассмотри два контура ABCDи ABMN. Для каждого из них выберем направление обхода.
Предположительно определим направление токов в каждом из элементов схемы. по второму закону Кирхгофа для контура ABCD имеем:
2 1 I2r2 I1r1 (1)
для контура ABMN имеем
1 I1r1 IR (2)
По первому закону Кирхгофа для узла N имеем
I I1 I2 (3)
Из уравнения (1) ток
2 1 I1r1 (4)
I2
r2
Вычислим:
![]() I2 2В 2В 1А
1Ом 0,5А.
I2 2В 2В 1А
1Ом 0,5А.
2Ом
Решаем систему уравнений методом подстановки, так как у нас есть три уравнения и три неизвестных.
Подставим найденное значение тока I2в уравнение (3), найдем ток
![]() I I1 I2, I 1A 0,5A
1,5A.
I I1 I2, I 1A 0,5A
1,5A.
Из уравнения (2) сопротивление
![]() I1r1 .
I1r1 .
R
I
Вычислим:
![]() R 2В
1A 1Ом 0,67Ом.
R 2В
1A 1Ом 0,67Ом.
1,5A
Ответ: I2 0,5А, I 1,5A, R 0,67Ом.
16. Чему равна сила тока в двигателе насоса, если при КПД 85 % насос ежеминутно подает 200 л воды на высоту 40 м? Напряжение питания двигателя 220 В. Дано:
η=85%, t = 1 мин=60 с, V = 200 л=0,2м3, h = 40 м,
U = 220 В.
Найти:
I– ?
Решение
КПД насоса
![]() А
А
П , (1)
АЗ
Полезная работа равна изменению потенциальной энергии
![]() АПmgh (2) m – масса воды, g –
ускорение свободного падения, h – высота на которую поднимают воду.
АПmgh (2) m – масса воды, g –
ускорение свободного падения, h – высота на которую поднимают воду.
Затраченная работа по закону Джоуля – Ленца
![]() АЗ I U t
(3)
АЗ I U t
(3)
![]() отсюда
отсюда
(4)
(5)
17. Электрический камин изготовлен из никелинового провода длиной 50,0 м и
2 сечением 1,4 мм . Определить мощность, потребляемую камином, и стоимость израсходованной за 2 ч энергии, если напряжение в сети 120 В, а тариф 1,24 руб. за 1 кВт·ч.
Дано:
l=50,0 м
S=1,4 мм2=1,4·10-6м2, t=2 ч,
U=120 В
Найти:
N=? ω=?
Решение:
Мощность потребляемую каминам найдем по формуле:
U 2
![]() N
N
R
где R – электрическое сопротивление провода.
l
R
S
где ρ=0,42·10-6 Ом·м – удельное сопротивление никелина.
U2S
N ,
l
1202В2 1,4 10 6 м2
![]()
![]() N 0,42
10 6Ом м 50м 960Вт0,96кВт
N 0,42
10 6Ом м 50м 960Вт0,96кВт
Стоимость израсходованной за 2 ч энергии
1,24Nt 1,24 0,96Вт 2ч 2,38руб
Ответ: N 0,96кВт , 2,38руб
1. Маленький шарик массой 2·10-3кг, подвешенный на тонкой нити, несет на себе заряд 3·10-7 Кл. На какое расстояние снизу к нему следует поднести другой маленький шарик с зарядом 5·10-7 Кл, чтобы натяжение нити уменьшилось в 2 раза? (Ответ: 37 см).
2. Заряды q1 = q2=q=1·10-6Кл расположены в вершинах равностороннего треугольника со сторонами 20 см. Найдите силу, действующую на один из этих зарядов со стороны двух других в воздухе. (Ответ: 0,38 Н).
3. Капелька массой 10-4г находится в равновесии в электрическом поле с напряженностью 98 Н/Кл. Найти величину заряда капельки. (Ответ: 10-8Кл).
4. Какую скорость приобретает электрон, пролетающий ускоряющую разность потенциалов 104В? (Ответ: 6·107 м/с).
5. Определите электроемкость конденсатора, для изготовления которого использовали ленту алюминиевой фольги длиной 157 см и шириной 90 мм. Толщина парафиновой бумаги 0,1 мм. Какая энергия запасена в конденсаторе, если он заряжен до рабочего напряжения 4·102В? (Ответ: 0,025 мкФ; 2 мДж).
6.Через поперечное сечение проводника каждую секунду протекает 12×109 свободных электронов. Определить силу тока в проводнике.
7.Какова э.д.с. источника напряжения, если сторонние силы совершают работу 10 Дж при разделении зарядов +5 и -5 Кл?
8.Э.д.с. источника тока равна 1,5 В. При замыкании источника сопротивлением 2 Ом сила тока составляет 0,3 А. Определить силу тока короткого замыкания.
9. Определить общее сопротивление участка цепи, в каждом из случаев, изображённых на рисунке. Сопротивление каждого проводника R = 1 Ом.
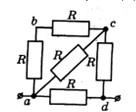
10. Определить силу токов, текущих в ветвях, если ε1 = 1 В, ε2 = 2 В, ε3 = 3В, r1 = 1 Ом, r2 =0,5 Ом, r3=1/3 Ом, R4 =1 Ом, R5 = 1/3Ом.
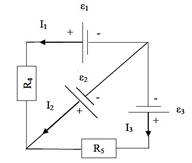 Рисунок
5.9 Вопросы для самоконтроля
Рисунок
5.9 Вопросы для самоконтроля
1. Что такое электрический заряд?
2. Чему равен заряд электрона?
3. Сформулируйте закон Кулона.
4. Что представляет собой электрическое поле и какими свойствами оно обладает?
5. Что называют напряженностью поля в данной его точке?
6. Что называют электрической силовой линией?
7. Какое поле называют однородным?
8. Сформулируйте принцип суперпозиций полей.
9. Зависит ли работа, совершаемая электрическим полем при перемещении заряда, от формы пути?
10. Что называют потенциалом поля в данной его точке?
11. Что называют эквипотенциальной поверхностью?
12. Как связаны напряженность и разность потенциалов электрического поля?
13. Что характеризует электрическая емкость проводника, от чего она зависит?
14. Какой конденсатор называют плоским? Чему равна его емкость?
15. Как рассчитать электрическую емкость батареи при параллельном и последовательном соединении конденсаторов?
16. Какое физическое явление называется электрическим током? Какими частицами в различных веществах создается электрический ток?
17. Какая физическая величина называется силой тока? В каких единицах измеряется сила тока? Какая физическая величина называется плотностью тока? В каких единицах измеряется плотность тока?
18. Какая физическая характеристика называется сопротивлением? В каких единицах измеряется? Чему равно сопротивление длинного проводника? Что характеризуется удельное сопротивление?
19. Как зависит сопротивление проводника от температуры? Какое физическое явление называется сверхпроводимостью?
20. Сформулируйте закон Ома для участка цепи.
21. Сформулируйте закон Ома в дифференциальной форме.
22. Какие силы называют сторонними? Приведите примеры сторонних сил. Что характеризует ЭДС? В каких единицах измеряется ЭДС?
23. Сформулируйте закон Ома для неоднородного участка цепи.
24. Сформулируйте закон Ома для замкнутой цепи.
25. Сформулируйте законы последовательного и параллельного соединения проводников и правила Кирхгофа.
5.1.Два одинаковых маленьких металлических шарика, имеющих заряды q1л и q2 , сближают в воздухе до соприкосновения, после чего разъединяют. Найдите силу взаимодействия F между шариками после удаления их на расстояние r друг от друга.

5. 2.В электрическом поле, вектор напряженности которого направлен вертикально вверх, неподвижно «весит» песчинка, заряд которой равен q. Масса песчинки равна m. Чему равен модуль вектора напряженности электрического поля.
|
Вариант |
а |
б |
в |
г |
д |
|
q, Кл |
2·10-11 |
2,5·10-11 |
3·10-11 |
3,5·10-11 |
4·10-11 |
|
m, кг |
10-6 |
1,5·10-6 |
1,2·10-6 |
1,7·10-6 |
2·10-6 |
|
Вариант |
е |
ж |
з |
и |
к |
|
q, Кл |
4,5·10-11 |
5·10-11 |
5,5·10-11 |
6·10-11 |
6,5·10-11 |
|
m, кг |
2,2·10-6 |
1,9·10-6 |
1,8·10-6 |
2,1·10-6 |
1,3·10-6 |
5.3. Два одинаковых шарика массой mкаждый подвешены на нитях длинойl. После того как шарикам были сообщены одинаковые заряды, они разошлись на расстояние r. Определить заряды шариков.
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
m, г |
0,5 |
0,3 |
0,35 |
0,4 |
0,17 |
0,22 |
0,33 |
0,24 |
0,19 |
0,2 |
|
l, см |
40 |
50 |
20 |
17 |
12 |
16 |
19 |
18 |
15,5 |
16,5 |
|
r, см |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
5,5 |
5.4. Расстояние между зарядами q1и q2равно r1. Какую работу надо совершит, чтобы перенести второй заряд в точку, находящуюся от первого заряда на расстоянии r2?
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
q1, нКл |
1 |
1,3 |
1,5 |
2 |
2,7 |
2,2 |
3 |
4 |
5 |
2,5 |
|
q2, нКл |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
7,5 |
8,5 |
9,5 |
|
r1, см |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
55 |
60 |
|
r2, м |
1 |
1,5 |
1,7 |
1,9 |
2 |
2,2 |
2,5 |
3 |
3,1 |
3,5 |
5.5.С каким ускорением движется электрон в поле с напряженностью Е? Заряд электрона 1,6·10-19Кл, масса электрона 9,1·10-31кг.
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
Е, кВ/м |
50 |
30 |
35 |
40 |
17 |
22 |
33 |
24 |
19 |
20 |
5. 6.Частица массой mи зарядомq, имеющая скорость υ, влетает в однородное электрическое поле напряженностью Eв направлении силовых линий поля. Какой путь она пролетит до остановки? Силой тяжести частицы пренебречь.
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
m, мг |
5 |
3 |
3,5 |
4 |
1,7 |
2,2 |
3.3 |
2,4 |
1,9 |
2 |
|
q, мКл |
-1,4 |
-1,5 |
-1,2 |
-1,7 |
-2 |
-2,2 |
-1,9 |
-1,8 |
-2,1 |
-1,3 |
|
υ, км/с |
1,5 |
2 |
2,5 |
3 |
3,5 |
4 |
4,5 |
5 |
5,5 |
6 |
|
Е, В/м |
100 |
120 |
130 |
150 |
170 |
200 |
250 |
350 |
300 |
400 |
5.7. Сколько электронов содержит заряд пылинки массой m, если она находится в состоянии равновесия в плоском конденсаторе, заряженном до напряжения U? Расстояние между пластинами равно d.
|
Вариант |
а |
б |
в |
г |
д |
|
m, мг |
2·10-6 |
2,5·10-6 |
3·10-6 |
3,5·10-6 |
4·10-6 |
|
U, В |
100 |
150 |
200 |
250 |
300 |
|
d, мм |
5 |
6 |
7 |
8 |
9 |
|
Вариант |
е |
ж |
з |
и |
к |
|
m, мг |
4,5·10-6 |
5·10-6 |
5,5·10-6 |
6·10-6 |
6,5·10-6 |
|
U, В |
350 |
400 |
450 |
500 |
550 |
|
d, мм |
10 |
11 |
12 |
13 |
14 |
5.8.Три конденсатора емкостью С1,С2 и С3соединен, как показано на схеме. Определить емкость системы конденсаторов.
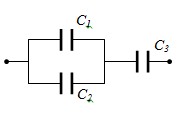
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
С1, мкФ |
5 |
3 |
3,5 |
4 |
1,7 |
2,2 |
3,3 |
2,4 |
1,9 |
2 |
|
С2, мкФ |
6 |
4 |
5 |
5 |
3 |
4 |
5,5 |
6 |
6,5 |
7 |
|
С3, мкФ |
7 |
8 |
9 |
10 |
8,5 |
9,5 |
10 |
7,7 |
8,6 |
9,2 |
5.9. Плоский конденсатор состоит из двух пластин площадью S каждая, расположенных на расстоянии d друг от друга. Между пластинами находится слой диэлектрика ε. Какой наибольший заряд можно сообщить конденсатору, если допустимое напряжение U.
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
S, см2 |
100 |
120 |
150 |
170 |
200 |
220 |
250 |
300 |
350 |
370 |
|
d, мм |
1 |
1,5 |
2 |
2,5 |
3 |
3,5 |
4 |
4,5 |
5 |
5,5 |
|
ε |
1 |
81 |
2,1 |
2,5 |
2,2 |
4,3 |
3,3 |
2 |
6 |
7 |
|
U, кВ |
1 |
1,5 |
2 |
2,5 |
3 |
3,5 |
2,8 |
3,1 |
3,6 |
2 |
5.10. Площадь пластины плоского воздушного конденсатора S, расстояние между ними d1, напряжение U. Конденсатор отключен от источника напряжения. На сколько изменится энергия конденсатора после раздвижения пластин до расстояния d2 между ними?
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
S, см2 |
100 |
120 |
150 |
170 |
200 |
220 |
250 |
300 |
350 |
370 |
|
d1, мм |
1 |
1,5 |
2 |
2,5 |
3 |
3,5 |
4 |
4,5 |
5 |
5,5 |
|
d2, мм |
1,5 |
2 |
2,5 |
3 |
3,5 |
4 |
4,5 |
5 |
5,5 |
6 |
|
U, В |
10 |
15 |
20 |
25 |
30 |
35 |
28 |
31 |
36 |
20 |
5.11.Что покажет гальванометр, если через него за время t прошел зарядq? Сколько электронов должно пройти в единицу времени через поперечное сечение проводника, чтобы включенный в цепь гальванометр показал силу токаI.
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
t, мин |
7 |
10 |
12 |
15 |
17 |
20 |
22 |
24 |
25 |
30 |
|
q,Кл |
1 |
1,5 |
3 |
3,2 |
3,5 |
3,7 |
4 |
5 |
6 |
10 |
|
I,A |
1 |
1,5 |
1,7 |
1,8 |
2 |
2,2 |
2,5 |
2,7 |
3 |
3,5 |
5.12.Найти сопротивление стального
проводника сечением S, если к нему приложено напряжение U. Средняя скорость
упорядоченного движения электронов в проводнике ![]() , а их
концентрация n.
, а их
концентрация n.
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
S, мм2 |
1 |
2 |
3 |
3,5 |
4 |
4,5 |
5 |
5,5 |
3,7 |
3 |
|
U,В |
50 |
55 |
60 |
65 |
70 |
75 |
80 |
85 |
90 |
100 |
|
|
1·10-4 |
1,5·10-4 |
2·10-4 |
2,5·10-4 |
3·10-4 |
3,5·10-4 |
4·10-4 |
5·10-4 |
6·10-4 |
7·10-4 |
|
n, м-3 |
4·1028 |
4,5·1028 |
5·1028 |
5,5·1028 |
6·1028 |
6,51028 |
7·1028 |
7,5·1028 |
8·1028 |
9·1028 |
5. 13.Катушка из медной проволоки имеет сопротивление R. Масса медной проволоки m. Сколько метровlпроволоки и какого диаметра d намотано на катушке? Плотность меди 8.6·103 кг/м3, удельное сопротивление меди 1,7·10-8 Ом·м.
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
R, Ом |
10 |
20 |
30 |
35 |
40 |
45 |
50 |
55 |
37 |
30 |
|
m,кг |
5 |
5,5 |
6 |
6,5 |
7 |
7,5 |
8 |
8,5 |
9 |
4 |
5.14. Определить силу тока короткого замыкания батареи, ЭДС которой ε, если при подключении к ней сопротивления R сила тока в цепи составляет I.
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
ε, B |
10 |
20 |
30 |
35 |
40 |
45 |
50 |
55 |
37 |
30 |
|
R, Ом |
5 |
5,5 |
6 |
6,5 |
7 |
7,5 |
8 |
8,5 |
9 |
4 |
|
I, A |
4 |
4,5 |
5 |
5,5 |
6 |
6,5 |
7 |
7,5 |
8 |
3 |
5.15. Найти сопротивление участка цепи, если сопротивление R.
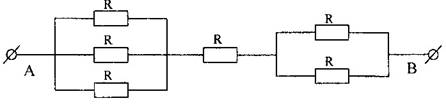
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
R, Ом |
1 |
2 |
3 |
3,5 |
4 |
4,5 |
5 |
5,5 |
3,7 |
2,5 |
5.16.Обмотка катушки из медной проволоки при температуре t имеет сопротивление R1. После пропускания тока сопротивление обмотки стало равно R2. До какой температуры нагрелась обмотка? Температурный коэффициент меди равен 4,15 10-3К-1
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
t, 0С |
10 |
20 |
30 |
35 |
40 |
45 |
50 |
55 |
37 |
30 |
|
R1, Ом |
5 |
5,5 |
6 |
6,5 |
7 |
7,5 |
8 |
8,5 |
9 |
4 |
|
R2, Ом |
7 |
8 |
8,5 |
9 |
9,5 |
10 |
10,5 |
11 |
11,5 |
6 |
5.17.Что показывает амперметр, включенный в цепь, если ЭДС источника ε, внутреннее сопротивление r, все сопротивления внешней цепи одинаковы и равны по 12 Ом?
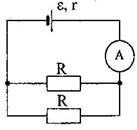
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
ε, B |
10 |
20 |
30 |
35 |
40 |
45 |
50 |
55 |
37 |
30 |
|
r, Ом |
5 |
5,5 |
6 |
6,5 |
7 |
7,5 |
8 |
8,5 |
9 |
4 |
5.18. Определить силу тока I в цепи (рисунке 5.13), если у каждого элемента ЭДС ε, а внутреннее сопротивление r.R1 = R2, R3, R4 ИR 5.
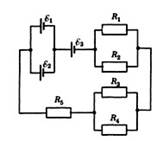
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
ε, B |
1 |
2 |
3 |
3,5 |
4 |
4,5 |
5 |
5,5 |
3,7 |
3 |
|
r, мОм |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
50 |
55 |
60 |
|
R1 =R2, Ом |
1 |
2 |
2,5 |
3 |
3,5 |
4 |
4,5 |
5 |
5,5 |
6 |
|
R3, Ом |
4 |
5 |
6 |
7 |
8 |
9 |
3,5 |
1,5 |
1,7 |
1,5 |
|
R4, Ом |
2 |
3 |
4 |
4,5 |
5 |
5,5 |
2,5 |
1 |
1,2 |
1 |
|
R5, Ом |
0,2 |
0,4 |
0,5 |
0,7 |
0,8 |
1 |
1,1 |
1,2 |
1,4 |
0,75 |
5.19. В схеме, изображённой на рисунке , ε1 , ε 2, R1 , и R2,R 3. Определить силу тока для каждого участка цепи. Внутренним сопротивлением источников тока пренебречь.
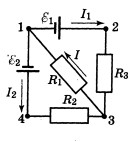
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
ε1, B |
1 |
2 |
3 |
3,5 |
4 |
4,5 |
5 |
5,5 |
3,7 |
3 |
|
ε2, B |
1,5 |
1,7 |
2 |
2,5 |
3 |
3,5 |
4 |
5 |
2,2 |
1,5 |
|
R1, Ом |
30 |
40 |
45 |
50 |
55 |
60 |
65 |
70 |
75 |
80 |
|
R2, Ом |
10 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
55 |
60 |
|
R3, Ом |
15 |
25 |
30 |
35 |
40 |
45 |
50 |
55 |
60 |
65 |
5.20. Аккумулятор с ЭДС ε и внутренним сопротивлением r,замкнут сопротивлением R.
Найдите мощность тока на внешнем участке цепи
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
ε, B |
1 |
2 |
3 |
3,5 |
4 |
4,5 |
5 |
5,5 |
1,5 |
2,5 |
|
r, Ом |
0,5 |
0,55 |
0,6 |
0,65 |
0,7 |
0,75 |
0,8 |
0,85 |
0,9 |
0,4 |
|
R, Ом |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
Номера задач, для индивидуального решения, выбираются согласно таблице вариантов
(Приложение А, таблица А3).
1.Дмитриева В.Ф. Физика для профессий и специальностей технического профиля. Сборник задач: учеб.пособие для студ. учреждений сред. проф. образования / В.Ф. Дмитриева. – 4ё–е изд., стер. – М.: Издательский центр «Академия», 2014. – 256 с. 2.Дмитриева В.Ф. Физика для профессий и специальностей технического профиля. Контрольные материалы: учеб.пособие для студ. учреждений сред. проф. образования/ В.Ф.
Дмитриева, Л. И. Васильев. – 3–е изд., стер. – М.: Издательский центр «Академия», 2014. – 112 с.
Тема: Магнитное поле. Электромагнитная индукция.
Цель: рассмотреть общие свойства магнитного поля и его характеристики; сформировать сознательное отношение к процессу обучения, стремление к самостоятельной работе; развить интерес к учебной дисциплине, содействовать активизации мышления и памяти у курсантов.
Краткие теоретические сведения
Таблица 6.1 – Основные законы и формулы
|
Физические законы, переменные |
|
Формулы |
|
|
Поле линейного проводника с током: где В – индукция магнитного поля; r – расстояние до проводника с током; I – сила тока:
r Направление B определяется по правилу буравчика (правого винта): направление вектора магнитной индукции совпадает с направлением вращения ручки буравчика (правого винта), который закручивают в направлении тока. r Направление B также определяется по правилу правой руки: если расположить пальцы правой руки так, чтобы большой палец указывал направление тока, то остальные четыре пальца покажут направление вектора магнитной индукции.
|
|
B |
I
|
|
Поле в центре витка с током: где R – радиус витка.
|
|
B |
|
|
Поле внутри соленоида: где N – число витков; l – длина соленоида. |
|
B |
|
|
Связь напряженности и индукции магнитного r поля: где H - вектор напряженности магнитного r поля; B - вектор индукции магнитного поля; μ0 = 4π·10-7Гн/м – магнитная постоянная,μ – магнитнаяпроницаемость
|
|
B |
r
|
|
Физические законы, переменные |
|
Формулы |
|
|
Сила Ампера: где I – сила тока; Δl – длина участка; В – модуль вектора магнитной индукции, α – угол r между вектором B и направлением тока в проводнике. |
FA |
|
|
|
r Направление FA определяется по правилу левой руки: если ладонь левой руки r расположить так, чтобы в нее «входил» B , а четыре вытянутых пальца расположить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы Ампера |
|
|
|
Сила Лоренца: где υ – скорость заряда, В – модуль вектора магнитной индукции, α – угол между r r r r
r
r Направление FЛ определяется по правилу левой руки: если ладонь левой руки r расположить так, чтобы в нее «входил» B , а четыре вытянутых пальца расположить по направлению скорости положительной частицы в проводнике, то отогнутый большой палец покажет направление силы Лоренца. |
|
|
|
Движение заряженной частицы в магнитном поле: 1) Радиус окружностиR, описываемой r
2) период вращения T, при условии, что
|
|
|
|
Магнитная проницаемость вещества: r r где B - магнитное поле в однородной среде; B0 - магнитное поле в вакууме. |
|
r
B0 |
|
Магнитный поток: где Ф – магнитный поток; S – площадь контура, α – угол между вектором магнитной индукции и нормалью к плоскости площадки.
|
Ф |
|
|
Физические законы, переменные |
Формулы |
|
|
Закон электромагнитной индукции: где εi – ЭДС индукции; N – число витков в катушке; ΔФ=Ф2– Ф1 – изменение магнитного потока; Δt – время. Правило Ленца: индукционный ток своим |
|
|
|
магнитным поем противодействует изменению магнитного потока, которым он вызван. |
|
|
|
ЭДС индукции в движущемся проводнике: В – модуль вектора магнитной индукции, Δl – длина участка; υ – скорость движения проводника; α – угол между вектором магнитной индукции и нормалью к плоскости площадки. |
|
|
|
Индуктивность катушки:
|
L
|
|
|
ЭДС самоиндукции: |
|
|
|
Энергия магнитного поля тока:
|
Wм
|
|
1.Определить значение модуля магнитной индукции в точке поля, удаленной на 3 см от бесконечно длинного проводника, по которому проходит ток 6 А.
Дано:
r = 3 см = 0,03м , I = 6 A
Найти: В– ?
Решение.
Магнитная индукция поля прямого проводника вычисляется по формуле:
В = 0I
2 r
Подставим числовые значения физических величин:
12,56 10 7 Гн 6А
B м 4 10 5Тл
![]() 2 3,14 0,03м Ответ:
В = 4 10 5 Тл.
2 3,14 0,03м Ответ:
В = 4 10 5 Тл.
2. Как расположены магнитные полюсы соленоида, подключенного к источнику тока?
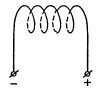
Решение

Вспомним, что за положительное направление тока принято направление от положительного полюса источника к отрицательному. Покажем направление тока на чертеже.
Направление вектора магнитной индукции, а следовательно, и магнитного полюса соленоида можно определить по правилу буравчика: если ввинчивать в соленоид буравчик так, чтобы вращение ручки буравчика совпадало с направлением тока в соленоиде, тогда поступательное движение буравчика будет совпадать с направлением вектора магнитной
индукции. Видно, что вектор магнитной индукции направлен справа налево, то есть буравчик r ввинчивают в этом направлении. Учитывая, что за направление вектора B принимается направление от южного полюса Sк северному полюсу N, то слева – северный полюс соленоида, справа – южный.
3.На проводник длиной 50 см, находящийся в однородном магнитном поле с магнитной индукцией 0,1 Тл, действует сила 0,05 Н. Вычислите угол между направлением силы тока и вектором магнитной индукции, если сила тока равна 2 А. Дано:
l = 50 см = 0,5 м,
В = 0,1 Тл, FА = 0,05Н, I = 2 А. Найти: α – ?
Решение
![]() На проводник
в магнитном поле, действует сила Ампера, модуль которой отсюда
На проводник
в магнитном поле, действует сила Ампера, модуль которой отсюда
4.Направление скорости движения электрона и полярность магнита указаны на рисунке. Определите направление силы, действующей на электрон.
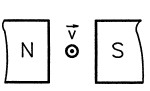
Решение.
На электрон, движущийся в магнитном поле, действует сила Лоренца, направление которой определим по правилу левой руки. Покажем на чертеже направление вектора магнитной индукции.
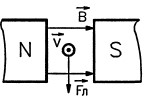
r Напомним, что вектор B направлен от северного полюса магнита N к южномуS.
r
![]() Электрон
движется на наблюдателя, так как на рисунке вектор изображен точкой. Левую
располагаем так, чтобы вытянутые четыре пальца указывали направление скорости
движения положительной частицы, то есть противоположное направление скорости заряда.
Вытянутые r четыре пальца должны
быть направлены от наблюдателя, вектор B упирается в ладонь.
Следовательно, сила Лоренца направлена вертикально вниз, как и отогнутый на 900
большой палец.
Электрон
движется на наблюдателя, так как на рисунке вектор изображен точкой. Левую
располагаем так, чтобы вытянутые четыре пальца указывали направление скорости
движения положительной частицы, то есть противоположное направление скорости заряда.
Вытянутые r четыре пальца должны
быть направлены от наблюдателя, вектор B упирается в ладонь.
Следовательно, сила Лоренца направлена вертикально вниз, как и отогнутый на 900
большой палец.
5.Протон, ускоренный разностью потенциалов U = 0,6кВ, влетая в однородное магнитное поле с магнитной индукцией В = 6 мТл, движется по окружности. Определите радиус этой окружности.
Дано:
U = 0,6кВ = 0,6·103В,
В = 6 мТл = 6·10-3Тл, Найти: R– ? Решение.
На протон в магнитном поле действует сила Лоренца
Fл q Bsin ,
где q – заряд протона, B – индукция магнитного поля, υ – скорость протона.
![]() Fл ,
тогда α = 900, sinα = 1, и
Fл ,
тогда α = 900, sinα = 1, и
Fл q B . (1)
Протон под действием силы Лоренца в магнитном поле движется по окружности с центростремительным ускорением. Согласно второму закону Ньютона
Fл, (2)
![]() Приравнивая уравнения
(1) и (2) получим m
Приравнивая уравнения
(1) и (2) получим m
отсюда
![]() .
(3)
.
(3)
(4).

Ответ: 0,6 м.
6.Круговой проволочный виток площадью S = 0,01 м2 находится в однородном магнитном поле, индукция которого В = 1 Тл. Плоскость витка перпендикулярна к направлению магнитного поля. Найти среднюю э.д.с. ε, возникающую в витке при выключении поля в течении t = 10 мс.
Дано:
S = 0,01 м2 В = 1 Тл t = 10 мс=0,01с Найти:
ε=?
Решение:
ЭДС индукции,возникающая в проволочном витке,равна скорости изменения магнитного потока: dФ i
dt
Изменение магнитного потока dФ BdS
![]() Таким
образом, искомая ЭДС индукции будет равна i B2 B1 S B1S dt t
Таким
образом, искомая ЭДС индукции будет равна i B2 B1 S B1S dt t
1Тл 0.01м2
i 1В
0,01с
Ответ: i 1В
7.Какое направление будет иметь индукционный ток в проводнике cd, если цепь с проводником ab замкнуть? разомкнуть? если ток в проводнике ab увеличить? уменьшить?
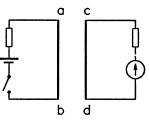
При замыкании цепи с проводником ab ток в ней устанавливается в направлении от a к b.
И вокруг проводника возникает магнитное поле, расположенное перпендикулярно плоскости r чертежа, а вектор магнитной индукции направлен на наблюдателя (направление вектора B определили по правилу буравчика).
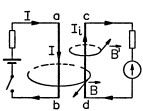
При замыкании цепи магнитный поток нарастает, ΔФ>0. По правилу Ленца устанавливаем, что индукционный ток должен иметь такое направление, чтобы создать
Br / . В данном магнитное поле с противоположным направлением вектора магнитной индукции случае вектор Br / будет направлен от наблюдателя.
По правилу буравчика определили, что ток в проводнике направлен от dк с. Такое направление будет иметь индукционный ток и в случае увеличения тока в цепи ab.
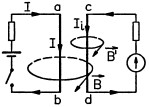
При размыкании цепи ab или при уменьшении тока в ней магнитный поток уменьшается, то есть ΔФ<0 и индукционный ток должен создавать магнитное поле, поддерживающее магнитное поле проводника ab (следуя правилу Ленца). Следовательно, вектор магнитной индукции поля, созданного индукционным током, и вектор магнитной индукции внешнего поля имеют одинаковое направление.
По правилу буравчика установили, что индукционный ток в проводнике cd направлен от
с к d.
8.Прямолинейный проводник с активной длиной l=0,45 м перемещается в однородном магнитном поле со скоростью υ=36 м/с под углом 70° к линиям поля. ЭДС, наведенная в нем, Е= 14,6 В. Определить напряженность магнитного поля. Дано:
l=0,45 м, υ=36 м/с, α = 70°, ε= 14,6 В.
Найти:
Н – ?
Решение
Для однородной изотропной среды вектор магнитной индукции:
![]()
где Н – вектор напряженности магнитного поля, μ0 – магнитная постоянная, μ –
магнитная проницаемость среды (в нашем случае μ =1), отсюда
Н
![]() . (1)
. (1)
Таким образом, для определения напряженности магнитного поля необходимо определить магнитную индукцию поля.
![]() При движении
проводника в магнитном поле в нем возникает ЭДС индукции где В – индукция
магнитного поля, l – длина активной части проводника, υ – скорость
При движении
проводника в магнитном поле в нем возникает ЭДС индукции где В – индукция
магнитного поля, l – длина активной части проводника, υ – скорость
(2)
.
9. Какая ЭДС самоиндукции возникает в катушке с индуктивностью 68 мГн, если ток 3,8 А исчезает в ней за 0,012 с?
Дано:
L = 68 мГн = 68·10-3Гн, ΔI = 3,8 А,
Δt = 0,012 с.
Найти:
εci – ?

10. Определить энергию магнитного поля катушки, в которой при токе 7,5 магнитный поток равен 2,3·10-3Вб. число витков в катушке 120. как изменится энергия поля, если сила тока изменится вдвое?
Дано:
I = 7,5 А, Ф=2,3·10-3Вб, N = 120.
Найти: W– ?

Подставим это выражение в формулу энергии магнитного поля. Получим,
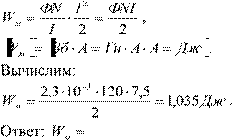 1,035Дж . Если сила тока уменьшится вдвое, то энергия поля
уменьшится в
1,035Дж . Если сила тока уменьшится вдвое, то энергия поля
уменьшится в
4 раза.
1.Зная направление вектора магнитной индукции, найти направление тока.
2.Какова индукция магнитного поля, в котором на проводник с током 25А действует сила 0,05Н? Длина активной части проводника 5см. Направления линий индукции и тока перпендикулярны.
3.Электрическая цепь, состоящая из четырех прямолинейных горизонтальных проводников (1-2, 2-3, 3-4, 4-1) и источника постоянного тока, находится в однородном r
магнитном поле, вектор магнитной индукции которого B направлен вертикально вверх (см.рис., вид сверху). Куда направлена вызванная этим полем сила Ампера, действующая на проводник 4-1?
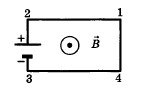
3.В однородное магнитное поле, линии индукции которого направлены от нас, влетает сверху протон. Как называется и как вычисляется сила, действующая со стороны магнитного поля на движущийся в нем электрический заряд? Нарисовать траекторию движения протона. Найдите скорость движения протона, если протон в поле с индукцией 0,01Тл, описал окружность радиусом 10см. Заряд протона равен 1.6·10-19кл, масса протона -1.67·10-27кг.
4.Плоскость замкнутого контура расположена под углом 450 к силовым линиям однородного магнитного поля. Что происходит с магнитным потоком при увеличении площади контура в 4 раза, и уменьшении магнитной индукции в 2 раза, если его ориентация не меняется.
5. Магнитный поток, пронизывающий контур проводника, равномерно изменился на 0,6 Вб за 0,5 с. Сопротивление проводника 0,24 Ом. Найдите силу индукционного тока.
6. Квадратная рамка со стороной 6,8 см, сделанная из медной проволоки с площадью поперечного сечения 1 мм2, помещена в однородное магнитное поле перпендикулярно линиям индукции. Индукция магнитного поля равномерно изменяется на 0,002 Тл за 0,1 с. Чему равна при этом сила тока в рамке? Удельное сопротивление меди 1,7·10-8Ом·м.
7. Замкнутая катушка из 100 витков помещена в однородное магнитное поле перпендикулярно ее оси. При изменении магнитного поля на 0,1 Тл за 0,1 св катушке выделяется 0,002 Дж тепла. Чему равно сопротивление катушки, если площадь поперечного сечения катушки 10 см2?
8. Проводник длиной 20 см движется в однородном магнитном поле со скоростью 3 м/с перпендикулярно силовым линиям. Найдите величину индукции магнитного поля, если на концах проводника возникает разность потенциалов 0,06 В.
9.На рисунке представлен график изменения силы тока с течением времени в катушке индуктивностью L = 6 мГн. Определите значение ЭДС самоиндукции.
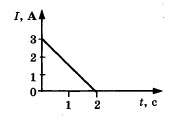
10.В катушке сила тока равномерно увеличивается со скоростью 2 А/с. при этом в ней возникает ЭДС самоиндукции 20 В. Какова энергия магнитного поля катушки при силе тока в ней 5 А?
1.Назовите условия существования магнитного поля. Охарактеризуйте магнитное поле.
2.Какая физическая величина называется магнитной индукцией? Как определяется направление вектора магнитной индукции?
3.В чем заключается принцип суперпозиции для магнитного поля?
4.Сформулируйте закон Ампера. Как определяется направление силы Ампера?
5.Сформулируйте закон Лоренца. Как определяется направление силы Лоренца?
6.Какая физическая величина называется потоком вектора магнитной индукцией? Как определяется поток вектора магнитной индукции?
7.В чем заключается явление электромагнитной индукции?
8.Сформулируйте закон электромагнитной индукции.
9.В чем заключается правило Ленца?
10.Какие токи называются вихревыми?
11.В чем заключается явление самоиндукции?
12.Чему равен коэффициент самоиндукции? В каких единицах измеряется коэффициент самоиндукции?
13.В чем заключается явление взаимной индукции?
14.Как определяется энергия магнитного поля?
15.Что характеризует объемная плотность энергии? Чему равна объемная плотность энергии электромагнитного поля?
6.1.Определите направление индукции магнитного поля в пространстве для случаев, показанных на рисунках.

(а) (б) (в) (г) (д) (е)
(ж) (з) (и) (к)
6.2.Прямолинейный проводник длиной l, по которому течет ток I, находится в
r однородном магнитном поле с индукцией В и расположен перпендикулярно вектору B . Каков модуль силы, действующей на проводник со стороны магнитного поля?
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
l, см |
10 |
15 |
17 |
20 |
22 |
25 |
30 |
32 |
35 |
40 |
|
I, А |
1 |
1,5 |
1,7 |
2 |
2,2 |
2,5 |
2,8 |
3 |
3,5 |
4 |
|
В, Тл |
0,1 |
0,3 |
0,5 |
0,8 |
1 |
1,2 |
1,5 |
1,7 |
2 |
2,5 |
6.3. На проводник длиной l, находящийся в однородном магнитном поле индукцией В, действует сила F. Вычислите угол между направлением силы тока и вектором магнитной индукции, если сила тока равна I.
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
l, см |
10 |
15 |
17 |
20 |
22 |
25 |
30 |
32 |
35 |
40 |
|
I, А |
1 |
1,5 |
1,7 |
2 |
2,2 |
2,5 |
2,8 |
3 |
3,5 |
4 |
|
В, Тл |
0,1 |
0,3 |
0,5 |
0,8 |
1 |
1,2 |
1,5 |
1,7 |
2 |
2,5 |
|
F, Н |
0,01 |
0,02 |
0,03 |
0,04 |
0,05 |
0,06 |
0,07 |
0,08 |
0,09 |
0,1 |
6.4.Проводник массой m и длиной l находится в равновесии в однородном магнитном поле индукцией В. Определите силу тока I, текущего по проводнику. Вектор магнитной индукции направлен горизонтально, перпендикулярно проводнику.
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
l, см |
10 |
15 |
17 |
20 |
22 |
25 |
30 |
32 |
35 |
40 |
|
m,г |
5 |
10 |
15 |
2 |
2,5 |
3 |
3,5 |
4 |
4,5 |
7 |
|
В, Тл |
0,1 |
0,3 |
0,5 |
0,8 |
1 |
1,2 |
1,5 |
1,7 |
2 |
2,5 |
6.5.Определите направление силы Ампера для случаев, показанных на рисунках
(а) (б) (в) (г)
 (д) (е) (ж) (з)
(д) (е) (ж) (з)
(и) (к)
6.6.Электрон движется по окружности радиусом R в однородном магнитном поле, имея импульс p. Определите модуль магнитной индукции поля. Заряд электрона e=-1,6·10-19 Кл.
|
Вариант |
а |
б |
в |
г |
д |
|
R, см |
0,5 |
0,8 |
1 |
1,2 |
1,5 |
|
p, кг·м/с |
2·10-23 |
3·10-23 |
4·10-23 |
4,5·10-23 |
5·10-23 |
|
Вариант |
е |
ж |
з |
и |
к |
|
R, см |
1,7 |
2 |
2,4 |
2,8 |
3 |
|
p, кг·м/с |
5,5·10-23 |
6·10-23 |
6,5·10-23 |
7·10-23 |
7,5·10-23 |
6.7.В однородном магнитном поле, индукция которого равна В, движется равномерно проводник длиной l. По проводнику течет ток I. Скорость движения проводника υ и направлена перпендикулярна к направлению магнитного поля. Найти работу перемещения проводника за время t.
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
l, см |
10 |
15 |
17 |
20 |
22 |
25 |
30 |
32 |
35 |
40 |
|
I, А |
1 |
1,5 |
1,7 |
2 |
2,2 |
2,5 |
2,8 |
3 |
3,5 |
4 |
|
В, Тл |
0,1 |
0,3 |
0,5 |
0,8 |
1 |
1,2 |
1,5 |
1,7 |
2 |
2,5 |
|
υ, см/с |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
|
t, с |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
6. 8.Электрон движется в вакууме в однородном магнитном поле с индукцией В. Радиус окружности, по которой он движется, равен R. Определите модуль скорости движения электрона, если она направлена перпендикулярно к линиям индукции.
|
Вариант |
а |
б |
в |
г |
д |
|
В, Тл |
10-3 |
3·10-3 |
4·10-3 |
5·10-3 |
6·10-3 |
|
R, см |
0,5 |
0,8 |
1 |
1,2 |
1,5 |
|
Вариант |
е |
ж |
з |
и |
к |
|
В, Тл |
7·10-3 |
8·10-3 |
9·10-3 |
10·10-3 |
15·10-3 |
|
R, см |
1,7 |
2 |
2,4 |
2,8 |
3 |
6.9. α – частица, кинетическая энергия которой Ек, влетает в однородное магнитное поле, перпендикулярное ее движению. Индукция магнитного поля В. Найти силу F, действующую на α – частицу, радиус R окружности, по которой движется α – частица, и период обращения Т α – частицы.
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
Ек, эВ |
100 |
150 |
200 |
250 |
300 |
350 |
400 |
450 |
500 |
550 |
|
В, Тл |
0,1 |
0,3 |
0,5 |
0,8 |
1 |
1,2 |
1,5 |
1,7 |
2 |
2,5 |
6.10.Контур площадью поперечного сечения S, помещен в однородное магнитное поле с индукцией В. Определите магнитный поток Ф, пронизывающий плоскость контура, если вектор индукции и нормаль к контуру: 1) сонаправлены; 2) противоположно направлены.
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
S, см2 |
50 |
70 |
80 |
100 |
120 |
150 |
170 |
200 |
220 |
250 |
|
В, мТл |
50 |
60 |
70 |
80 |
90 |
100 |
120 |
150 |
170 |
200 |
6.11.Найдите скорость изменения магнитного потока в соленоиде из N витков при возбуждении в нем ЭДС индукции ε.
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
N |
1000 |
1500 |
2000 |
2500 |
3000 |
3500 |
4000 |
4500 |
5000 |
5500 |
|
ε, В |
50 |
100 |
150 |
170 |
200 |
250 |
300 |
350 |
400 |
500 |
6. 12.Какой заряд пройдет через поперечное сечение витка, сопротивление которого R, при уменьшении магнитного потока внутри витка на ΔФ.
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
R, Ом |
0,01 |
0,02 |
0,03 |
0,04 |
0,05 |
0,06 |
0,07 |
0,08 |
0,09 |
0,1 |
|
ΔФ, мВб |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
25 |
30 |
35 |
6.13. Проводник длиной l движется в однородном магнитном поле со скоростью υ, направленной под углом αк линиям магнитной индукции. Найдите ЭДС индукции, возникающую в проводнике, если индукция магнитного поля В.
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
l, см |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
55 |
|
α0 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
60 |
70 |
|
υ, м/с |
1 |
3 |
5 |
7 |
8 |
9 |
10 |
12 |
14 |
15 |
|
В, мТл |
5 |
7 |
8 |
9 |
10 |
12 |
15 |
17 |
20 |
25 |
6.
14.Проводящее кольцо, площадью S и сопротивлением R, помещено в
однородное магнитное поле так, что плоскость кольца перпендикулярна линиям
индукции поля. Какое количество теплоты выделится в кольце за Δt, если
индукция магнитного поля убывает со скоростью ![]() .
.
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
S, м2 |
0,1 |
0,15 |
0,2 |
0,25 |
0,3 |
0,35 |
0,4 |
0,45 |
0,5 |
0,55 |
|
R, Ом |
0,001 |
0,002 |
0,003 |
0,004 |
0,005 |
0,006 |
0,007 |
0,008 |
0,009 |
0,01 |
|
Δt, с |
0,1 |
0,3 |
0,5 |
0,8 |
1 |
1,2 |
1,5 |
1,7 |
2 |
2,5 |
|
|
0,02 |
0,04 |
0,06 |
0,08 |
0,1 |
0,15 |
0,2 |
0,25 |
0,3 |
0,35 |
6.15. В катушке, состоящей из 75 витков, магнитный поток равен 4,8·10-3 Вб. За какое время должен исчезнуть этот поток, чтобы в катушке возникла средняя ЭДС индукции 0,74 В?
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
N |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
120 |
|
Ф, Вб |
2·10-3 |
3·10-3 |
4·10-3 |
5·10-3 |
6·10-3 |
7·10-3 |
8·10-3 |
10·10-3 |
11·10-3 |
12·10-3 |
|
ε, В |
0,5 |
0,7 |
0,9 |
1 |
1,2 |
1,4 |
1,5 |
1,7 |
1,9 |
2 |
6.16. Катушка диаметром d находится в переменном магнитном поле, силовые линии которого параллельны оси катушки. При изменении индукции поля на ΔB в течении Δt в катушке возникла ЭДС ε. Сколько витков имеет катушка.
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
d, см |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
12 |
|
ΔВ, Тл |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Δt, c |
5 |
7 |
8 |
9 |
10 |
12 |
15 |
17 |
20 |
25 |
|
ε, В |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
6.17.Катушка из N витков площадью витка S расположена в однородном магнитном
r
поле индукцией В перпендикулярно вектору B . За время Δt магнитный поток сквозь катушку убыл до нуля, при этом возникла ЭДС индукции ε . сколько витков N содержит катушка.
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
S, м2 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
55 |
|
В, Тл |
0,5 |
0,1 |
0,15 |
0,2 |
0,25 |
0,3 |
0,35 |
0,4 |
0,45 |
0,5 |
|
Δt, с |
0,01 |
0,03 |
0,05 |
0,08 |
1 |
1,2 |
1,5 |
1,7 |
2 |
2,5 |
|
ε, В |
0,2 |
0,4 |
0,6 |
0,8 |
0,1 |
0,15 |
0,2 |
0,25 |
0,3 |
0,35 |
6.18.В катушке, индуктивность которой равна L, возникла ЭДС самоиндукции, равная ε.
Рассчитайте изменение силы тока и энергии магнитного поля катушки, если это произошло за
Δt.
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
L, Гн |
0,1 |
0,15 |
0,2 |
0,25 |
0,3 |
0,35 |
0.4 |
0,45 |
0,5 |
0,55 |
|
ε, В |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
55 |
60 |
65 |
|
Δt, с |
0,1 |
0,3 |
0,5 |
0,8 |
1 |
1,2 |
1,5 |
1,7 |
2 |
2,5 |
6.19.Определите индуктивность проводника, в котором равномерное изменение силы тока на ΔIв течение времени Δtс возбуждает ЭДС самоиндукции ε.
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
ΔI, А |
1 |
1,5 |
2 |
2,5 |
3 |
3,5 |
4 |
4,5 |
5 |
5,5 |
|
Δt, с |
0,1 |
0,3 |
0,5 |
0,8 |
1 |
1,2 |
1,5 |
1,7 |
2 |
2,5 |
|
ε, мВ |
20 |
40 |
60 |
80 |
100 |
120 |
140 |
160 |
180 |
200 |
6.20.При силе тока в катушке I энергия магнитного поля в ней равна Wм. Определите магнитный поток, идущий через катушку.
|
Вариант |
а |
б |
в |
г |
д |
е |
ж |
з |
и |
к |
|
I, А |
0,1 |
0,15 |
0,2 |
0,25 |
0,3 |
0,35 |
0,4 |
0,45 |
0,5 |
0,55 |
|
Wм, Дж |
0,1 |
0,3 |
0,5 |
0,8 |
1 |
1,2 |
1,5 |
1,7 |
2 |
2,5 |
Номера задач, для индивидуального решения, выбираются согласно таблице вариантов
(Приложение А, таблица А4).
1.Дмитриева В.Ф. Физика для профессий и специальностей технического профиля. Сборник задач: учеб.пособие для студ. учреждений сред. проф. образования / В.Ф. Дмитриева. – 4ё–е изд., стер. – М.: Издательский центр «Академия», 2014. – 256 с.
2.Дмитриева В.Ф. Физика для профессий и специальностей технического профиля. Контрольные материалы: учеб.пособие для студ. учреждений сред. проф. образования/ В.Ф.
Дмитриева, Л. И. Васильев. – 3–е изд., стер. – М.: Издательский центр «Академия», 2014. – 112 с.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
Основные источники:
1.Дмитриева В.Ф. Физика для профессий и специальностей технического профиля:
учебник для образоват. учреждений нач. и сред.проф. образования/ В.Ф. Дмитриева. – 5–е изд., стер. – М.: Издательский центр «Академия», 2014. – 448 с.
2.Дмитриева В.Ф. Физика для профессий и специальностей технического профиля. Сборник задач: учеб.пособие для студ. учреждений сред. проф. образования / В.Ф. Дмитриева. – 4ё–е изд., стер. – М.: Издательский центр «Академия», 2014. – 256 с.
3.Дмитриева В.Ф. Физика для профессий и специальностей технического профиля. Контрольные материалы: учеб.пособие для студ. учреждений сред. проф. образования/ В.Ф.
Дмитриева, Л. И. Васильев. – 3–е изд., стер. – М.: Издательский центр «Академия», 2014. – 112 с.
4.Попова Т.Н.,Кузьменко С.Н.,Масленникова Д.Ю.,Прудкий А.С.,Гаджилов М.В.Конспект лекцийдля студентов дневной и заочной форм обучения,обучающихся по направлению:6.040106 –Экология, охрана окружающей среды и сбалансированное природопользование, 2014 г.
Дополнительные источники:
1.Самойленко П.И. Физика учебник для средних специальных заведений/ П.И
Самойленко, - Ф.В.Сергеева Москва «Академия»2014. - 321 с
2.Самойленко П.И. Физика учебник для средних специальных заведений/ П.И Самойленко, - Ф.В.Сергеева Москва «Академия»2014. - 268 с
3.Трофимова Т.И. Курс физики с примерами решения задач в 2 т. Т. 1-2: учебник/ Т.И. Трофимова, А.В. Фирсов. – М: КНОРУС, 2015.
Интернет -источники:
1.Министерство образования и науки РФ www.mon.gov.ru
2. Российский образовательный портал www.edu.ru
3. Департамент образования Тверской области www.edu.tvel.ru
4.Тверской областной институт усовершенствования www.tiuu.ru
5.Представление опыта работы, класс физика physicam.ru>profskill/22/50.htm
Таблица вариантов для индивидуальной работы №А1
|
Вариант |
|
|
|
|
Номер задачи |
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
1 |
1.1а |
1.4и |
1.6к |
1.9з |
1.13а |
2.2д |
2.5а |
2.8б |
2.11б |
2.14е |
|
2 |
1.2и |
1.5а |
1.8а |
1.11б |
1.14е |
2.3е |
2.6а |
2.9в |
2.12а |
2.15в |
|
3 |
1.2з |
1.5г |
1.8ж |
1.12и |
1.15а |
2.1а |
2.4к |
2.7а |
2.10ж |
2.13в |
|
4 |
1.1г |
1.4б |
1.7а |
1.10г |
1.13з |
2.3д |
2.6в |
2.9г |
2.12е |
2.15д |
|
5 |
1.3ж |
1.6а |
1.9ж |
1.12б |
1.15з |
2.1к |
2.4а |
2.7и |
2.10а |
2.13к |
|
6 |
1.1е |
1.4г |
1.8е |
1.10и |
1.13ж |
2.2и |
2.5з |
2.8а |
2.11в |
2.14д |
|
7 |
1.3е |
1.6з |
1.9и |
1.11ж |
1.14ж |
2.1з |
2.4и |
2.7ж |
2.10е |
2.13и |
|
8 |
1.1з |
1.4е |
1.7з |
1.12к |
1.15и |
2.3г |
2.6б |
2.9д |
2.12к |
2.15к |
|
9 |
1.3д |
1.6д |
1.9б |
1.11и |
1.14д |
2.2е |
2.5ж |
2.8з |
2.11г |
2.14к |
|
10 |
1.2а |
1.4з |
1.7б |
1.10д |
1.13к |
2.3ж |
2.6г |
2.9е |
2.12б |
2.15г |
|
11 |
1.2б |
1.5в |
1.8б |
1.12в |
1.15е |
2.1в |
2.4б |
2.7з |
2.10к |
2.13а |
|
12 |
1.3в |
1.6е |
1.9е |
1.11г |
1.14б |
2.2к |
2.5б |
2.8в |
2.11а |
2.14ж |
|
13 |
1.2д |
1.4в |
1.7и |
1.10к |
1.13и |
2.3а |
2.6д |
2.9к |
2.12ж |
2.15ж |
|
14 |
1.3а |
1.6г |
1.10а |
1.12г |
1.15б |
2.1е |
2.4з |
2.7б |
2.10д |
2.13б |
|
15 |
1.3к |
1.7в |
1.10з |
1.12а |
1.15ж |
2.3з |
2.6е |
2.9ж |
2.12з |
2.15и |
|
16 |
1.1ж |
1.4к |
1.6б |
1.9а |
1.13б |
2.2а |
2.5е |
2.8ж |
2.11д |
2.14и |
|
17 |
1.2ж |
1.5д |
1.8в |
1.11е |
1.14в |
2.1и |
2.4в |
2.7е |
2.10б |
2.13ж |
|
18 |
1.1д |
1.6ж |
1.9в |
1.12д |
1.15в |
2.2б |
2.5и |
2.8г |
2.11е |
2.14г |
|
19 |
1.3и |
1.7е |
1.10е |
1.12е |
1.15д |
2.3и |
2.6к |
2.9з |
2.12в |
2.15е |
|
20 |
1.1в |
1.6и |
1.9д |
1.12з |
1.15к |
2.1б |
2.4ж |
2.7в |
2.10з |
2.13г |
|
21 |
1.2в |
1.5е |
1.8и |
1.11д |
1.14а |
2.2ж |
2.5в |
2.8е |
2.11ж |
2.14а |
|
22 |
1.5к |
1.8г |
1.3б |
1.11а |
1.14и |
2.3б |
2.6и |
2.9б |
2.12и |
2.15з |
|
23 |
1.1б |
1.4д |
1.7г |
1.10в |
1.13е |
2.1д |
2.4г |
2.7к |
2.10и |
2.13з |
|
24 |
1.3г |
1.6в |
1.9г |
1.11в |
1.14з |
2.3к |
2.6ж |
2.9и |
2.12г |
2.15б |
|
25 |
1.2г |
1.5и |
1.8д |
1.12ж |
1.15г |
2.2з |
2.5к |
2.8д |
2.11з |
2.14в |
|
26 |
1.1и |
1.4ж |
1.7д |
1.10ж |
1.13д |
2.2в |
2.5г |
2.8и |
2.11к |
2.14з |
|
27 |
1.3з |
1.5ж |
1.8к |
1.11з |
1.14к |
2.1г |
2.4д |
2.7г |
2.10в |
2.13е |
|
28 |
1.2е |
1.5б |
1.8з |
1.11к |
1.14г |
2.3в |
2.6з |
2.9а |
2.12д |
2.15а |
|
29 |
1.1к |
1.4а |
1.7ж |
1.10б |
1.13г |
2.1ж |
2.4е |
2.7д |
2.10г |
2.13д |
|
30 |
1.2к |
1.5з |
1.7к |
1.9к |
1.13в |
2.2г |
2.5д |
2.8к |
2.11и |
2.14б |
А2
|
Вариант |
|
|
|
Номер задачи |
|
|
||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
1 |
3.1а |
3.4и |
3.6к |
3.9з |
4.2д |
4.5а |
4.8б |
4.5з |
|
2 |
3.2и |
3.5а |
3.8а |
3.6з |
4.3е |
4.6а |
4.9в |
4.7ж |
|
3 |
3.2з |
3.5г |
3.8ж |
3.4в |
4.1а |
4.4к |
4.7а |
4.10ж |
|
4 |
3.1г |
3.4б |
3.7а |
3.10г |
4.3д |
4.6в |
4.9г |
4.4б |
|
5 |
3.3ж |
3.6а |
3.9ж |
3.7в |
4.1к |
4.4а |
4.7и |
4.10а |
|
6 |
3.1е |
3.4г |
3.8е |
3.10и |
4.2и |
4.5з |
4.8а |
4.7з |
|
7 |
3.3е |
3.6з |
3.9и |
3.5д |
4.1з |
4.4и |
4.7ж |
4.10е |
|
8 |
3.1з |
3.4е |
3.7з |
3.10е |
4.3г |
4.6б |
4.9д |
4.5б |
|
9 |
3.3д |
3.6д |
3.9б |
3.8и |
4.2е |
4.5ж |
4.8з |
4.9к |
|
10 |
3.2а |
3.4з |
3.7б |
3.10д |
4.3ж |
4.6г |
4.9е |
4.7б |
|
11 |
3.2б |
3.5в |
3.8б |
3.3б |
4.1в |
4.4б |
4.7з |
4.10к |
|
12 |
3.3в |
3.6е |
3.9е |
3.7г |
4.2к |
4.5б |
4.8в |
4.6е |
|
13 |
3.2д |
3.4в |
3.7и |
3.10к |
4.3а |
4.6д |
4.9к |
4.8ж |
|
14 |
3.3а |
3.6г |
3.10а |
3.9г |
4.1е |
4.4з |
4.7б |
4.10д |
|
15 |
3.3к |
3.7в |
3.10з |
3.5ж |
4.3з |
4.6е |
4.9ж |
4.7е |
|
16 |
3.1ж |
3.4к |
3.6б |
3.9а |
4.2а |
4.5е |
4.8ж |
4.6к |
|
17 |
3.2ж |
3.5д |
3.8в |
3.9в |
4.1и |
4.4в |
4.7е |
4.10б |
|
18 |
3.1д |
3.6ж |
3.9в |
3.8к |
4.2б |
4.5и |
4.8г |
4.6к |
|
19 |
3.3и |
3.7е |
3.10е |
3.6е |
4.3и |
4.6к |
4.9з |
4.5в |
|
20 |
3.1в |
3.6и |
3.9д |
3.4а |
4.1б |
4.4ж |
4.7в |
4.10з |
|
21 |
3.2в |
3.5е |
3.8и |
3.7ж |
4.2ж |
4.5в |
4.8е |
4.6ж |
|
22 |
3.5к |
3.8г |
3.3б |
3.4ж |
4.3б |
4.6и |
4.9б |
4.7к |
|
23 |
3.1б |
3.4д |
3.7г |
3.10в |
4.1д |
4.4г |
4.7к |
4.10и |
|
24 |
3.3г |
3.6в |
3.9г |
3.5б |
4.3к |
4.6ж |
4.9и |
4.8и |
|
25 |
3.2г |
3.5и |
3.8д |
3.9е |
4.2з |
4.5к |
4.8д |
4.6з |
|
26 |
3.1и |
3.4ж |
3.7д |
3.10ж |
4.2в |
4.5г |
4.8и |
4.7г |
|
27 |
3.3з |
3.5ж |
3.8к |
3.4в |
4.1г |
4.4д |
4.7г |
4.10в |
|
28 |
3.2е |
3.5б |
3.8з |
3.2ж |
4.3в |
4.6з |
4.9а |
4.5д |
|
29 |
3.1к |
3.4а |
3.7ж |
3.10б |
4.1ж |
4.4е |
4.7д |
4.10г |
|
30 |
3.2к |
3.5з |
3.7к |
3.9к |
4.2г |
4.5д |
4.8к |
4.4ж |
А3
|
Вариант |
|
|
Номер задачи |
|
|||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
1 |
5.1а |
5.4и |
5.6к |
5.9з |
5.13а |
5.16к |
5.19д |
|
2 |
5.2и |
5.5а |
5.8а |
5.11б |
5.14е |
5.16з |
5.19и |
|
3 |
5.2з |
5.5г |
5.8ж |
5.12и |
5.15а |
5.17б |
5.20а |
|
4 |
5.1г |
5.4б |
5.7а |
5.10г |
5.13з |
5.17и |
5.20е |
|
5 |
5.3ж |
5.6а |
5.9ж |
5.12б |
5.15з |
5.18а |
5.19ж |
|
6 |
5.1е |
5.4г |
5.8е |
5.10и |
5.13ж |
5.18е |
5.20з |
|
7 |
5.3е |
5.6з |
5.9и |
5.11ж |
5.14ж |
5.16ж |
5.19е |
|
8 |
5.1з |
5.4е |
5.7з |
5.12к |
5.15и |
5.17е |
5.18е |
|
9 |
5.3д |
5.6д |
5.9б |
5.11и |
5.14д |
5.18б |
5.20и |
|
10 |
5.2а |
5.4з |
5.7б |
5.10д |
5.13к |
5.18д |
5.17г |
|
11 |
5.2б |
5.5в |
5.8б |
5.12в |
5.15е |
5.18ж |
5.19к |
|
12 |
5.3в |
5.6е |
5.9е |
5.11г |
5.14б |
5.16е |
5.18г |
|
13 |
5.2д |
5.4в |
5.7и |
5.10к |
5.13и |
5.17в |
5.19а |
|
14 |
5.3а |
5.6г |
5.10а |
5.12г |
5.15б |
5.18з |
5.17а |
|
15 |
5.3к |
5.7в |
5.10з |
5.12а |
5.15ж |
5.17а |
5.19з |
|
16 |
5.1ж |
5.4к |
5.6б |
5.9а |
5.13б |
5.16д |
5.20б |
|
17 |
5.2ж |
5.5д |
5.8в |
5.11е |
5.14в |
5.18и |
5.17б |
|
18 |
5.1д |
5.6ж |
5.9в |
5.12д |
5.15в |
5.16и |
5.20д |
|
19 |
5.3и |
5.7е |
5.10е |
5.12е |
5.15д |
5.18г |
5.17в |
|
20 |
5.1в |
5.6и |
5.9д |
5.12з |
5.15к |
5.17к |
5.19б |
|
21 |
5.2в |
5.5е |
5.8и |
5.11д |
5.14а |
5.16в |
5.20в |
|
22 |
5.5к |
5.8г |
5.3б |
5.11а |
5.13и |
5.18к |
5.20ж |
|
23 |
5.1б |
5.4д |
5.7г |
5.10в |
5.13е |
5.16г |
5.18д |
|
24 |
5.3г |
5.6в |
5.9г |
5.11в |
5.14з |
5.17г |
5.19в |
|
25 |
5.2г |
5.5и |
5.8д |
5.12ж |
5.15г |
5.16б |
5.18в |
|
26 |
5.1и |
5.4ж |
5.7д |
5.10ж |
5.13д |
5.17д |
5.19г |
|
27 |
5.3з |
5.5ж |
5.8к |
5.11з |
5.14к |
5.18в |
5.20г |
|
28 |
5.2е |
5.5б |
5.8з |
5.11к |
5.14г |
5.16а |
5.20к |
|
29 |
5.1к |
5.4а |
5.7ж |
5.10б |
5.13г |
5.17ж |
5.18а |
|
30 |
5.2к |
5.5з |
5.7к |
5.9к |
5.13в |
5.17з |
5.18б |
А4
|
Вариант |
|
|
Номер задачи |
|
|||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
1 |
6.1а |
6.4и |
6.6к |
6.9з |
6.13а |
6.16к |
6.19д |
|
2 |
6.2и |
6.5а |
6.8а |
6.11б |
6.14е |
6.16з |
6.19и |
|
3 |
6.2з |
6.5г |
6.8ж |
6.12и |
6.15а |
6.17б |
6.20а |
|
4 |
6.1г |
6.4б |
6.7а |
6.10г |
6.13з |
6.17и |
6.20е |
|
5 |
6.3ж |
6.6а |
6.9ж |
6.12б |
6.15з |
6.18а |
6.19ж |
|
6 |
6.1е |
6.4г |
6.8е |
6.10и |
6.13ж |
6.18е |
6.20з |
|
7 |
6.3е |
6.6з |
6.9и |
6.11ж |
6.14ж |
6.16ж |
6.19е |
|
8 |
6.1з |
6.4е |
6.7з |
6.12к |
6.15и |
6.17е |
6.18е |
|
9 |
6.3д |
6.6д |
6.9б |
6.11и |
6.14д |
6.18б |
6.20и |
|
10 |
6.2а |
6.4з |
6.7б |
6.10д |
6.13к |
6.18д |
6.17г |
|
11 |
6.2б |
6.5в |
6.8б |
6.12в |
6.15е |
6.18ж |
6.19к |
|
12 |
6.3в |
6.6е |
6.9е |
6.11г |
6.14б |
6.16е |
6.18г |
|
13 |
6.2д |
6.4в |
6.7и |
6.10к |
6.13и |
6.17в |
6.19а |
|
14 |
6.3а |
6.6г |
6.10а |
6.12г |
6.15б |
6.18з |
6.17а |
|
15 |
6.3к |
6.7в |
6.10з |
6.12а |
6.15ж |
6.17а |
6.19з |
|
16 |
6.1ж |
6.4к |
6.6б |
6.9а |
6.13б |
6.16д |
6.20б |
|
17 |
6.2ж |
6.5д |
6.8в |
6.11е |
6.14в |
6.18и |
6.17б |
|
18 |
6.1д |
6.6ж |
6.9в |
6.12д |
6.15в |
6.16и |
6.20д |
|
19 |
6.3и |
6.7е |
6.10е |
6.12е |
6.15д |
6.18г |
6.17в |
|
20 |
6.1в |
6.6и |
6.9д |
6.12з |
6.15к |
6.17к |
6.19б |
|
21 |
6.2в |
6.5е |
6.8и |
6.11д |
6.14а |
6.16в |
6.20в |
|
22 |
6.5к |
6.8г |
6.3б |
6.11а |
6.13и |
6.18к |
6.20ж |
|
23 |
6.1б |
6.4д |
6.7г |
6.10в |
6.13е |
6.16г |
6.18д |
|
24 |
6.3г |
6.6в |
6.9г |
6.11в |
6.14з |
6.17г |
6.19в |
|
25 |
6.2г |
6.5и |
6.8д |
6.12ж |
6.15г |
6.16б |
6.18в |
|
26 |
6.1и |
6.4ж |
6.7д |
6.10ж |
6.13д |
6.17д |
6.19г |
|
27 |
6.3з |
6.5ж |
6.8к |
6.11з |
6.14к |
6.18в |
6.20г |
|
28 |
6.2е |
6.5б |
6.8з |
6.11к |
6.14г |
6.16а |
6.20к |
|
29 |
6.1к |
6.4а |
6.7ж |
6.10б |
6.13г |
6.17ж |
6.18а |
|
30 |
6.2к |
6.5з |
6.7к |
6.9к |
6.13в |
6.17з |
6.18б |
Справочные материалы. Табличные данные.
Таблица Б1 – Основные физические постоянные (округленные значения)
|
Физическая постоянная |
Обозначение |
Значение |
|
Нормальное ускорение свободного падения |
g |
9,81 м/с2 |
|
Гравитационная постоянная |
G |
6,67·10-11 м2/кг·с2 |
|
Средний радиус Земли |
R |
6,37·106 м |
|
Постоянная Авогадро |
NA |
6,02·1023 моль-1 |
|
Универсальная газовая постоянная |
R |
8,31 Дж/моль·К |
|
Молярный объем идеального газа при нормальных условиях |
Vm |
22,4·10-3 м3/моль |
|
Нормальное атмосферное давление |
P0 |
101325Па = 760 мм рт. ст. = = 1 Бар = 1 атм ≈ 1·105 Па |
|
Постоянная Больцмана |
k |
1,38·10-23 Дж/к |
|
Элементарный заряд |
e |
1,6·10-19 Кл |
|
Скорость света в вакууме |
c |
3·108 м/с |
|
Электрическая постоянная |
ε0 |
8,85·10-12 Ф/м |
|
Магнитная постоянная |
μ0 |
4π·10-7 Гн/м (Н/А2) |
|
Атомная единица массы |
mаем |
1 а.е.м=1,66·10-27 кг = = 931,42 МэВ |
|
Масса нейтрона |
mn |
1,66·10-27 кг = 939,57 МэВ |
|
Масса протона |
mp |
1,673·10-27 кг = 938,28 МэВ |
|
Масса электрона |
me |
9,1·10-31 кг = 0,511 МэВ |
Таблица Б2– Моменты инерции однородных тел массой m, имеющих правильную геометрическую форму и равномерное распределение массы по объему
|
Тело |
Положение оси вращения |
Момент инерции |
|
Полый тонкостенный цилиндр радиуса R |
Ось симметрии |
mR2 |
|
Сплошной цилиндр или диск радиуса R |
Ось симметрии |
|
|
Прямой тонкий стержень длиной l |
Ось перпендикулярна стержню и проходит через его середину |
|
|
Шар радиусом R |
Ось проходит через центр шара |
|
|
Вещество |
α (К-1) |
Вещество |
k (К-1) |
|
Вольфрам |
4,6·10-3 |
Нихром Х20Н80 |
0,2·10-3 |
|
Константан |
0,1·10-3 |
Реотан |
0,4·10-3 |
|
Манганин |
0,03·10-3 |
Фехраль |
0,1·10-3 |
|
Никелин |
0,02·10-3 |
Таблица Б3 – Множители и приставки СИ для образования десятичных кратных и дольных единиц и их наименований
|
Множитель |
Приставка |
Обозначение |
|
1018 |
экса |
Э |
|
1015 |
пета |
П |
|
1012 |
тера |
Т |
|
109 |
гига |
Г |
|
106 |
мега |
М |
|
103 |
кило |
к |
|
102 |
гекто |
г |
|
101 |
дека |
да |
|
10-1 |
деци |
д |
|
10-2 |
санти |
с |
|
10-3 |
милли |
м |
|
10-6 |
микро |
мк |
|
10-9 |
нано |
н |
|
10-12 |
пико |
п |
|
10-15 |
фемто |
ф |
|
10-18 |
атто |
а |
Таблица Б4 – Диэлектрическая проницаемость некоторых веществ
|
Вещество |
ε |
Вещество |
ε |
|
Анилин |
84 |
Лед (при – 18 оС) |
3,2 |
|
Бензин |
2,3 |
Масло трансформаторное |
2,2÷2,5 |
|
Вакуум |
1 |
Мрамор |
8÷9 |
|
Вода |
81 |
Парафин |
2,0 |
|
Вода (при 0оС) |
88 |
Резинка |
2÷3 |
|
Водород |
1,0003 |
Рутил |
130 |
|
Воздух (при 1 атм.) |
1,0006 |
Сера |
3,6÷4,3 |
|
Воздух (при 100 атм.) |
1,055 |
Слюда |
6÷9 |
|
Воск |
5,8 |
Стекло |
5÷10 |
|
Глицерин |
39 |
Фарфор |
4÷7 |
|
Дерево |
3,5÷5,0 |
Эбонит |
2,7 |
|
Керосин |
2,0 |
Янтарь |
2,8 |
Таблица Б5 – Физические свойства некоторых твердых тел
|
Твердое тело |
|
|
Удельная теплоемкость при 20 оС |
Удельная теплота плавления (при температуре плавления) |
||
|
Дж/кг·К |
Кал/г·град |
Дж/кг· |
Кал/г |
|||
|
Алюминий |
2600 |
659 |
896 |
0,314 |
3,22·105 |
77 |
|
Железо |
7900 |
1530 |
500 |
0,119 |
1,25·105 |
30 |
|
Латунь |
8400 |
900 |
386 |
0,092 |
– |
– |
|
Лед |
900 |
0 |
2100 |
0,5 |
3,35·105 |
80 |
|
Медь |
8600 |
1100 |
395 |
0,094 |
1,76·105 |
42 |
|
Олово |
7100 |
232 |
230 |
0,055 |
5,86·104 |
14 |
|
Платина |
21400 |
1770 |
117 |
0,028 |
1,13·105 |
27 |
|
Свинец |
11300 |
327 |
126 |
0,030 |
2,26·104 |
5,4 |
|
Серебро |
10500 |
960 |
234 |
0,056 |
8,8·104 |
21 |
|
Сталь |
7700 |
1300 |
460 |
0,11 |
– |
– |
|
Цинк |
7000 |
420 |
391 |
0,093 |
1,17·105 |
28 |
Таблица 6 – Физические свойства некоторых жидкостей
|
Жидкость |
Плотность, кг/м3 |
Удельная теплоемкость при 20 оС |
Коэффициент поверхностного натяжения при |
|
|
|
|
|||
|
|
|
Дж/кг·К |
Кал/г·град |
20 оС, Н/м |
|
Бензол |
880 |
1720 |
0,41 |
0,03 |
|
Вода |
1000 |
4190 |
1,0 |
0,073 |
|
Глицерин |
1200 |
2430 |
0,58 |
0,064 |
|
Керосин |
800 |
2140 |
0,051 |
0,03 |
|
Ртуть |
13600 |
138 |
0,033 |
0,5 |
|
Спирт |
790 |
2510 |
0,5 |
0,02 |
Таблица 8 – Удельное сопротивление некоторых веществ
|
Вещество |
ρ (Ом·м) |
Вещество |
ρ (Ом·м) |
|
Алюминий |
2,7·10-8 |
Олово |
1,13·10-7 |
|
Вольфрам |
5,3·10-8 |
Осмий |
9,5·10-8 |
|
Железо |
9,9·10-8 |
Платина |
2,03·10-7 |
|
Золото |
2,2·10-8 |
Реотан |
4,5·10-7 |
|
Константан |
4,7·10-7 |
Ртуть |
9,54·10-7 |
|
Латунь |
6,3·10-8 |
Свинец |
2,07·10-7 |
|
Манганин |
3,9·10-7 |
Серебро |
1,58·10-8 |
|
Медь |
1,68·10-8 |
Уголь |
(4,0÷5,0)·10-5 |
|
Никелин |
4,2·10-7 |
Фехраль |
1,118·10-6 |
|
Никель |
7,3·10-8 |
Цинк |
3,388·10-7 |
|
Нихром |
1,05·10-6 |
Уколова Юлия Валериевна
ПРАКТИКУМ
для курсантов специальности
26.02.05 Эксплуатация судовых энергетических установок очной формы обучения
Судомеханический техникум ФГБОУ ВО
«Керченский государственный морской технологический университет»
298309 г. Керчь, Орджоникидзе, 123
[1] Моменты инерции однородных тел массой m, имеющих правильную геометрическую форму и равномерное распределение массы по объему см. Приложение Б2
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.