Гра m x n

Гра m x n

У принципі рішення будь-якої матричної гри зводиться до рішення стандартного завдання лінійного програмування й, тим самим, може бути знайдено методами лінійного програмування. При цьому необхідний обсяг обчислень прямо залежить від числа чистих стратегій гравців (росте з його збільшенням й, виходить, зі збільшенням розмірів матриці гри). Тому будь-які прийоми попереднього аналізу гри, що дозволяють зменшувати розміри її платіжної матриці або ще якось спрощувати цю матрицю, не наносячи збитку рішенню, грають на практиці досить важливу роль.

Правило домінування

У цілому ряді випадків аналіз платіжної матриці виявляє, що деякі чисті стратегії не можуть внести ніякого внеску в шукані оптимальні змішані стратегії. Відкидання подібних стратегій дозволяє замінити первісну матрицю на матрицю виграшів менших розмірів.

Опишемо одну з таких можливостей більш докладно.

Нехай

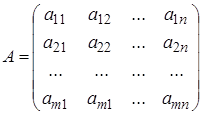
- довільна m х n -матриця. Будемо говорити, що i-я рядок матриці А

не більше j-й рядка цієї матриці

якщо одночасно виконані наступні п нерівностей

При цьому кажуть також, що j-я рядок домінує i-ю рядок, або що стратегія  A_j гравця А домінує стратегію Ai.

Зауваження. Гравець діятиме розумно, якщо буде уникати стратегій, яким у матриці гри відповідають домінуючі рядки.

Якщо в матриці А один з рядків (j-я) домінує інший рядок (i-ю), то число рядків у матриці А можна зменшити шляхом відкидання домінуючого рядка (i-й).

Далі, будемо говорити, що k-й стовбець матриці А

не менше l-го стовпця цієї матриці

якщо одночасно виконані наступні m нерівностей

При цьому говорять також, що l-й стовбець домінує k-й стовбець, або що стратегія В_l гравця В домінує стратегію Bk.

Зауваження. Гравець У діятиме розумно, якщо буде уникати стратегій, яким у матриці гри відповідають домінуючі стовбці.

Якщо в матриці А один зі стовбців (l-й) домінує інший стовбець (k-й), то число стовбців у матриці А можна зменшити шляхом відкидання домінуючого  стовпця (k-гo).

1.        Зауваження. Оптимальні змішані стратегії в грі з матрицею, отриманої усіканням вихідної за рахунок домінуючих рядків і стовпців, дадуть оптимальне рішення у вихідній грі: Домінуючі чисті стратегії гравців у змішанні не беруть участь - відповідні їм імовірності варто взяти рівними нулю.

Аффинне правило

При пошуку рішення матричних ігор часто виявляється корисним наступна властивість.

Припустимі перетворення матриці гри і її ціна. Оптимальні стратегії в матричних ігор, елементи матриць А и С яким зв'язані рівностями

де , а – довільно, мають однакові рівноважні ситуації (або в чистих, або в змішаних стратегіях), а їхньої ціни задовольняють наступній умові

Основні етапи пошуку рішення матричних ігор

1-й етап – перевірка наявності (або відсутності) рівноваги в чистих стратегіях (при наявності рівноважної ситуації вказуються відповідні оптимальні стратегії гравців і ціна гри).

2-й етап – пошук домінуючих стратегій (у випадку успіху цього пошуку — відкидання домінуючих рядків і стовпців у вихідній матриці гри).

3-й етап – заміна гри на її змішане розширення й відшукання оптимальних змішаних стратегій і ціни гри.