Ігри 2 x 2

Ігри 2 x 2

Найбільш простим випадком кінцевої гри є гра 2x2, де в кожного гравця є дві стратегії. Розглянемо гру 2x2 з матрицею:

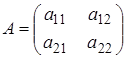
Тут можуть зустрітися 2 ситуації:

1.        гра має сідлову точку;

2.         гра не має сідлову точку.

У першому випадку рішення очевидно: це пари стратегій, що перетинаються в сідловій. Якщо ж сідловок точки немає, то рішення повинне бути в змішаних стратегіях.

Знайдемо його, тобто пари оптимальних змішаних стратегій гравців А и В

,     

Спочатку визначимо оптимальну змішану стратегію для гравця А.

Якщо ми будемо дотримуватися цієї стратегії, то незалежно від способу дій супротивника, виграш буде залишатися рівним ціні гри . У грі 2x2 обидві стратегії супротивника є активними. Виходить, якщо ми дотримуємося своєї оптимальної стратегії , то супротивник може, не міняючи виграшу, застосовувати кожну зі своїх чистих стратегій.

На підставі теореми про активні стратегії для гравця , що застосовує оптимальну змішану стратегію  й гравця , що застосовує свою чисту стратегію , ціна гри буде така ж , тому

.

Для випадку, коли  приймає стратегію , а гравець  приймає свою чисту стратегію , ціна гри буде теж , тому

.

Звідси маємо два рівняння:

                                                                                              (1)

з яких, беручи до уваги рівність , одержимо систему:

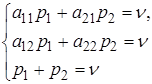                                                                                            (2)

Рішенням гри  будуть вираження:

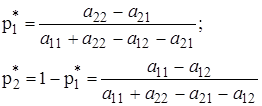                       ;                                                (3)

Ціну гри  знайдемо, підставляючи в кожне з рівнянь (1) значення :

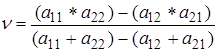                                           .                                      (4)

Аналогічно міркуючи, можна одержати систему рівнянь для знаходження оптимальної змішаної стратегії гравця  й ціну гри:

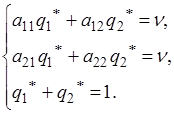                                                                                           (5)

Звідки одержуємо:

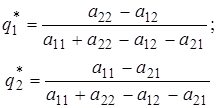                                                   .                            (6)