Гри 2 x n

Гри 2 x n

1.        Наші розгляди ми почнемо з матричних ігор, число стратегій хоча б одного із гравців у яких дорівнює двом.

Для побудови рішень 2 х п и тх2 ігор існує ефективний метод, заснований на простих геометричних міркуваннях. Цей метод називають графічним.

Нехай А=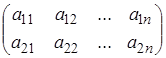 – платіжна матриця 2 х п гри.

Відповідно до теореми про подвійний опис гри (теорема 2) знаходження ціни гри й оптимального значення р° для гравця А рівносильне рішенню рівняння

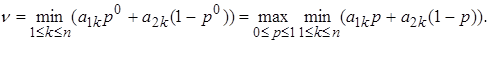
Опишемо загальну схему, що приводить до шуканого результату. Максимум функції           

                                                                                        (1)                                                     

найпростіше знайти, побудувавши її графік.

Для цього надходять у такий спосіб. Припустимо, що гравець А вибрав змішану стратегію Р = {р, 1 – р}, а гравець В – k-ю чисту стратегію, k = 1, 2, ... , п. Тоді середній виграш гравця А в ситуації {Р, k} виявляється рівним

На площині (р, w) рівняння (k) описує пряму. Тим самим, кожної чистої стратегії гравця В на цій площині відповідає своя пряма. Тому спочатку на площині (w, р) послідовно й акуратно рисуються всі прямі (мал. 2).

Потім для кожного значення р, 0 £ р£ 1, шляхом візуального порівняння відповідних йому значень w на кожній з побудованих прямих визначається й відзначається мінімальне з них (мал. 3).

У результаті описаної процедури виходить ламана, яка і є графіком функції (1) (виділена жирним на мал. 4). Ця ламана як би обгинає знизу все сімейство побудованих прямих, і із цієї причини її прийнято називати нижньою. огибающей цього сімейства.

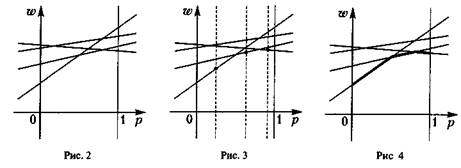
Верхня точка побудованої нижньої що обгинає визначає й ціну гри – v й оптимальну стратегію гравця А – Р° = {р°, 1 – р⁰} .

Зауваження. Описана процедура може розглядатися як деякий аналог максимінного підходу при відсутності сідлової точки.

2.        Однак у ряді випадків виявляється важливим знати оптимальні змішані стратегії обох гравців.

Як шукається оптимальна змішана стратегія гравця А, ми вже описали. Покажемо тепер, як відшукати оптимальну змішану стратегію гравця В.

1.        Тут, залежно від форми нижньої що обгинає, може виникти кілька випадків.

А). Нижня що обгинає має рівно одну найвищу крапку (р°, w°):

А. 1) Якщо р° = 0 (оптимальна стратегія гравця А – чиста стратегія А₂), те гравцеві У вигідно застосовувати чисту стратегію, що відповідає номеру прямої, що проходить через крапку (0, w°) і яка має найбільший негативний нахил (мал. 8).

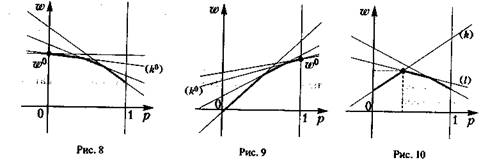
А. 2) Якщо р° = 1 (оптимальна стратегія гравця А – чиста стратегія А₁), то оптимальною для гравця В є чиста стратегія, що відповідає номеру прямої, що проходить через крапку (1, w°) і яка має найменший позитивний нахил (мал. 9).

А. 3) Якщо 0 < р° < 1, то в найвищій крапці нижньої що обгинає перетинаються, щонайменше, дві прямі, одна з яких (k-я) має позитивний нахил, а інша (l-я) – негативний (мал. 10), і оптимальна змішана стратегія гравця У виходить, якщо покласти

де q – рішення рівняння

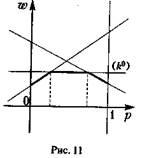
Б). Нижня що обгинає містить горизонтальну ділянку, що відповідає чистої стратегії k° гравця В, що й є оптимальною для нього (мал. 11).

1.3. m x 2 гри.

Нехай тепер у матричній грі дві чисті стратегії має гравець В, а число чистих стратегій у гравця А довільно (дорівнює m). Це означає, що платіжна матриця такої гри має вигляд

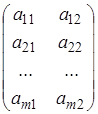
Аналіз такої гри багато в чому нагадує міркування, описані для гри 2 х n.

Нехай  – довільна змішана стратегія гравця В. Якщо гравець А вибирає i-ю чисту стратегію,  i = 1, 2, ... , т, те середній виграш гравця В у ситуації {i, Q} буде рівним

                                                                (2)

Залежність цього виграшу від змінної q описується прямій.

Графіком функції

є верхня огибающая сімейства прямих (2), що відповідають чистим стратегіям гравця А (мал. 12).

Абсцисою нижньої точки отриманої ламаної буде значення q°, що визначає оптимальну змішану стратегію гравця В, а ординатою w° – ціна гри.

Зауваження. Відшукання оптимальної змішаної стратегії гравця А проводиться по тій же схемі, що дозволяє знаходити оптимальну змішану стратегію гравця В у грі 2 х n.