
Модели повышенной сложности.
1. Стохастические модели.
При изучении экономических явлений часто используют модели вероятностного типа. Они отличаются от детерминических моделей. Детерминические модели не использую случайных явлений и их связи во времени.
Стохастические модели используют взаимозависимость случайных явлений во времени. Стохастические модели существуют со времени возникновения теории вероятностей. Примерами таких моделей можно считать схему бросания кости или выбор карты.
Если в относительных величинах анализируемых детерминистскими моделями существует стабильность а случайными отклонениями пренебрегают, то в стохастических моделях учитываются случайные отклонения.
Задание: подготовить проект одной стохастической модели, которая включает в себя случайное отклонение.
В экономике стохастические модели имеют наибольшее применение, т.к. экономические отклонения на рынке распространены и они имеют случайный характер.
Кроме экономики случайные процессы моделируются в психологии и педагогике, биологии. Для модели соответствующей данному предмету приходится генерировать случайное число, либо в языках программирования, либо в прикладных сферах. Но генерация случайных чисел, это не создание модели полностью.
При вычислении площади криволинейной трапеции используется формула учитывающая случайности (метод Монте-Карло)
Рассмотрим пример экономической задачи, в которой присутствует случайное отклонение.
Если рассмотреть экономическую модель, то она моделирует поведение групп станков поточной линии. Перед каждым станком имеется страховой задел (Si). Этот задел содержит детали необходимые для обеспечения станка необходимыми деталями. При недостатке страхового задела станки будут простаивать и это приведёт к снижению производительности линии. Задача сводится к нахождению страхового задела, который минимизирует издержки производства. Пусть линия состоит из m станков, zi – число полуфабрикатов поступающих на i станок после i-1 операции.
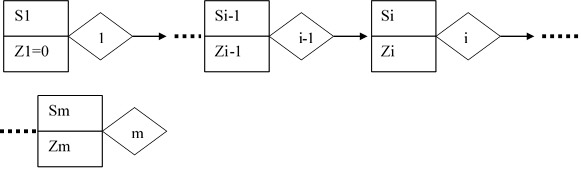 |
Будем предполагать, что поломки любого станка распределяются равномерно в течении главного периода работы (Т) линии . Исправление неисправности станка занимает небольшое время по сравнению с Т работой линии. Задача: найти оптимальный страховой задел s1,s2,s3,…,sm.
В такой постановке задача может быть решена методом динамического программирования, который основан на двух принципах:
1. Пошаговое конструктивное решение
2. Оптимальность
Этапность решения задачи следующая: конструируется целевая функция на первом шаге для последнего станка, находится оптимальный страховой задел Sm. На втором шаге записывается целевая функция для двух последних станков и находится Sm-1 и …Sm. И так далее пока не найдём S1.
Обозначим через ti – время работы i-го станка за период Т. Для задания этой величины надо задать закон распределения ti.
Fi(t) - плотность распределения ti.
Pi – штраф i-го станка в единицу времени.
Hi – стоимость детали после i-1 операции.
λi – производительность i-го станка в единицу времени.
τi – простой i-го станка.
Выводим τi следующим образом:
τi =![]()
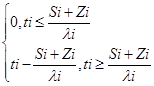
τi – случайная величина.
По формуле из теории вероятностей определяется математическое ожидание затрат для i-го станка из-за его простоев:
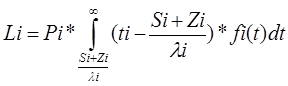 -
математическое ожидание затрат для i –го
станка.
-
математическое ожидание затрат для i –го
станка.
Обозначим через ri число неиспользованных деталей после окончания работы линии.
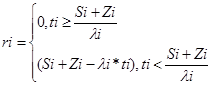
Определим по готовой формуле математическое ожидание неиспользованных деталей для этого станка.
L1i=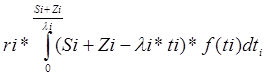 - математическое ожидание неиспользуемых деталей для i-го станка.
- математическое ожидание неиспользуемых деталей для i-го станка.
Составим уравнение характеризующее работу для поточной линии.
1. Qm=Lm+L1m – математическое ожидание затрат от простоев неиспользованных деталей. Находим min значение Qm с помощью оптимизации полученной функции.
2. Находим Qm-1=Lm-1+L1m-1 затраты для m-1 станка. Находится min оптимизационной функции
3. …
m. Q1=L1+L11
Таким образом задача сводится к системе уравнений в которых находится min целевых функций для любого станка.
Решить эти уравнения или найти целевую функцию можно либо составлением программы, либо графическим методом линейного программирования, но в любом случае система уравнений представляет собой стохастическую модель для описания экономического процесса.
Пример использования системы дифференциальных уравнений в биологии.
Примером использования системы дифференциальных уравнений в биологии является модель биоценоза с учётом введённых допущений.
![]()
![]()
N1 –число жертв.
N2 –число хищников.
α1 – коэффициент естественного прироста жертв.
α2 – коэффициент естественной убыли хищников.
β1 – коэффициент уничтожения хищниками своих жертв.
β2 – коэффициент защиты жертв от хищников.
Уравнение приводится к нормированному виду – это освобождение от всяких масштабных единиц, тогда система имеет вид:
![]()
![]()
где ![]()
![]() относительное число жертв.
относительное число жертв.
![]() относительное
число хищников.
относительное
число хищников.
τ- нормированное время.
B=![]() -
коэффициент.
-
коэффициент.
Данная система решается в среде MathCad, здесь же строятся графики зависимости х от τ и у от τ.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.