БЮДЖЕТНОЕ УЧРЕЖДЕНИЕ

ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

ХАНТЫ-МАНСИЙСКОГО АВТОНОМНОГО ОКРУГА – ЮГРЫ «СОВЕТСКИЙ ПОЛИТЕХНИЧЕСКИЙ КОЛЛЕДЖ»

УТВЕРЖДАЮ

Заместитель директора

по учебной работе

____________/Н.Н. Болдырева/

«___»_______2023г.

Комплект контрольно-оценочных средств

для оценки результатов освоения

ОДБ.07 «Математика»

  по специальности

54.02.01 Дизайн (по отраслям)

г. Советский, 2023 г.

Комплект контрольно-оценочных средств по учебной дисциплине ОДБ.07 «Математика» разработан  на основе Федерального государственного образовательного стандарта среднего общего образования (утв. приказом Министерства образования и науки РФ от «17» мая 2012 г. № 413)

Организация-разработчик: бюджетное учреждение профессионального образования Ханты -Мансийского автономного округа-Югры «Советский политехнический колледж»

Разработчик:

Невенкина О.И.,   преподаватель бюджетного учреждения профессионального образования Ханты-Мансийского автономного округа-Югры «Советский политехнический колледж»

I.   ПАСПОРТ КОМПЛЕКТА ОЦЕНОЧНЫХ СРЕДСТВ

Общие положения

Учебная дисциплина ОДБ.07 «Математика» изучается на 1 и 2 курсах.

Максимальное количество часов на реализацию программы УД – 236.

Практикоориентированность учебной дисциплины составляет 49 %.

Учебная дисциплина ОДБ.07 «Математика»  состоит из 4 разделов:

Раздел 1. Алгебра

Раздел 2. Геометрия

Раздел 3. Элементы комбинаторики, теории вероятностей и математической статистики

Раздел 4. Начала математического анализа

Профиль получаемого профессионального образования: технологический.

Реализация программы учебной дисциплины способствует формированию у обучающихся:

Личностных результатов обучения:

            Метапредметных результатов обучения:

МР01. Умение самостоятельно определять цели деятельности и составлять планы деятельности; самостоятельно осуществлять, контролировать и корректировать деятельность; использовать все возможные ресурсы для достижения поставленных целей и реализации планов деятельности; выбирать успешные стратегии в различных ситуациях;

МР02. Умение продуктивно общаться и взаимодействовать в процессе совместной деятельности, учитывать позиции других участников деятельности, эффективно разрешать конфликты;

МР03. Владение навыками познавательной, учебно-исследовательской и проектной деятельности, навыками разрешения проблем; способность и готовность к самостоятельному поиску методов решения практических задач, применению различных методов познания;

МР04. Готовность и способность к самостоятельной информационно-познавательной деятельности, владение навыками получения необходимой информации из словарей разных типов, умение ориентироваться в различных источниках информации, критически оценивать и интерпретировать информацию, получаемую из различных источников;

МР05. Умение использовать средства информационных и коммуникационных технологий (далее – ИКТ) в решении когнитивных, коммуникативных и организационных задач с соблюдением требований эргономики, техники безопасности, гигиены, ресурсосбережения, правовых и этических норм, норм информационной безопасности;

МР07. Умение самостоятельно оценивать и принимать решения, определяющие стратегию поведения, с учётом гражданских и нравственных ценностей;

МР08. Владение языковыми средствами – умение ясно, логично и точно излагать свою точку зрения, использовать адекватные языковые средства;

МР09. Владение навыками познавательной рефлексии как осознания совершаемых действий и мыслительных процессов, их результатов и оснований, границ своего знания и незнания, новых познавательных задач и средств их достижения.

      Предметных результатов:

ПРб 01. Сформированность представлений о математике как части мировой культуры и о месте математики в современной цивилизации, о способах описания на математическом языке явлений реального мира;

ПРб 02. Сформированность представлений о математических понятиях как о важнейших математических моделях, позволяющих описывать и изучать разные процессы и явления; понимание возможности аксиоматического построения математических теорий;

ПРб 03.  Владение методами доказательств и алгоритмов решения; умение их применять, проводить доказательные рассуждения в ходе решения задач;

ПРб 04. Владение стандартными приёмами решения рациональных и иррациональных, показательных, степенных, тригонометрических уравнений и неравенств, их систем; использование готовых компьютерных программ, в том числе для поиска пути решения и иллюстрации решения уравнений и неравенств;

ПРб 05. Сформированность представлений об основных понятиях, идеях и методах математического анализа;

ПРб 06. Владение основными понятиями о плоских и пространственных геометрических фигурах, их основных свойствах; сформированность умения распознавать на чертежах, моделях и в реальном мире геометрические фигуры; применение изученных свойств геометрических фигур и формул для решения геометрических задач и задач с практическим содержанием;

ПРб 07. Сформированность представлений о процессах и явлениях, имеющих вероятностный характер, о статистических закономерностях в реальном мире, об основных понятиях элементарной теории вероятностей; умений находить и оценивать вероятности наступления событий в простейших практических ситуациях и основные характеристики случайных величин;

ПРб 08. Владение навыками использования готовых компьютерных программ при решении задач.

ПРу 01. Сформированность представлений о необходимости доказательств при обосновании математических утверждений и роли аксиоматики в проведении дедуктивных рассуждений;

ПРу 02. Сформированность понятийного аппарата по основным разделам курса математики; знаний основных теорем, формул и умения их применять; умения доказывать теоремы и находить нестандартные способы решения задач;

ПРу 03. Сформированность умений моделировать реальные ситуации, исследовать построенные модели, интерпретировать полученный результат;

ПРу 04. Сформированность представлений об основных понятиях математического анализа и их свойствах, владение умением характеризовать поведение функций, использование полученных знаний для описания и анализа реальных зависимостей;

ПРу 05. Владение умениями составления вероятностных моделей по условию задачи и вычисления вероятности наступления событий, в том числе с применением формул комбинаторики и основных теорем теории вероятностей; исследования случайных величин по их распределению.

Общие компетенции:

ОК 01. Выбирать способы решения задач профессиональной деятельности применительно к различным контекстам;

ОК 02. Использовать современные средства поиска, анализа и интерпретации информации и информационные технологии для выполнения задач профессиональной деятельности;

ОК 03. Планировать и реализовывать собственное профессиональное и личностное развитие, предпринимательскую деятельность в профессиональной сфере, использовать знания по финансовой грамотности в различных жизненных ситуациях;

ОК 04. Эффективно взаимодействовать и работать в коллективе и команде;

ОК 05.  Осуществлять устную и письменную коммуникацию на государственном языке Российской Федерации с учетом особенностей социального и культурного контекста;

ОК 06. Проявлять гражданско-патриотическую позицию, демонстрировать осознанное поведение на основе традиционных общечеловеческих ценностей, в том числе с учетом гармонизации межнациональных и межрелигиозных отношений, применять стандарты антикоррупционного поведения;

ОК 07. Содействовать сохранению окружающей среды, ресурсосбережению, применять знания об изменении климата, принципы бережливого производства, эффективно действовать в чрезвычайных ситуациях.

Контроль формируемых знаний и умений проводится в процессе текущего контроля. Промежуточная аттестация предусмотрена в форме экзамена на втором курсе в четвертом семестре.

Матрицы логических связей между объектами (предметами) контроля и разделами (темами) учебной дисциплины ОУД.05 «Математика»

II. Комплект оценочных средств

2.1. Комплект материалов для оценки сформированности личностных, метапредметных и предметных результатов по дисциплине ОДБ.07 «Математика»

2.1.1 Задания для входного контроля

Шкала оценки образовательных достижений

ВАРИАНТ № 1

В1. В результате сравнения чисел  -4/7 и -5/8  получилось: а) -4/7> - 5/8;  б) -4/7<-5/8; в) -4/7= -5/8.

В2. Разложите на множители:                                                                                                                 а) 1 – 64в²;  б) а³ – 4а;  в) 2х² + 5х – 3.

В3. Летом килограмм клубники стоит 70 рублей. Маша купила 3 кг 200 г клубники. Сколько рублей сдачи она должна получить с 250 рублей?

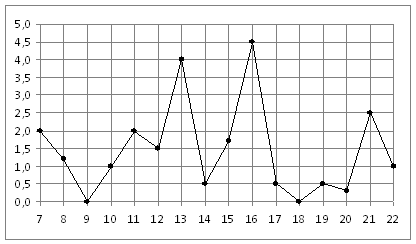
В4. На рисунке жирными точками показано суточное количество осадков, выпадавших в Мурманске с 7 по 22 ноября 1995 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какое наибольшее количество осадков выпадало в период с 7 по 14 февраля. Ответ дайте в миллиметрах.

В5.  Чему равно значение выражения   при а=?

                   1) - 9;          2) - ;           3)  ;           4) 9.

В6.

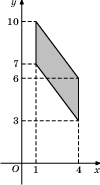
В7. Найдите площадь параллелограмма, вершины которого имеют координаты (1;7), (4;3), (4;6), (1;10).

В8. В прямоугольном треугольнике один из катетов равен 10, а острый угол, прилежащий к нему, равен . Найдите площадь треугольника.

В9. Лодка в 5:00 вышла из пункта А в пункт В, расположенный в 30 км от А. Пробыв в пункте В 2 часа, лодка отправилась назад и вернулась в пункт А в 23:00 того же дня. Определите (в км/ч) скорость течения реки, если известно, что собственная скорость лодки равна 4 км/ч.

В10. Какое из данных чисел не входит в область определения выражения   ?

                   1) 2;          2) 0;           3)  -4;           4) -2.

В11. Решите уравнение:  а) х (х -5) = - 4.   б)

В12. Решите неравенство х² + х – 6 < 0.

В13. Найдите вершину параболы:  а) у = - х² -4х + 1.

В14. Запишите координаты точек пересечения графика функции у = 3х² + 5х – 2  с осью ординат.

В15. Решите систему уравнений 

ВАРИАНТ № 2

В1.    В результате сравнения чисел  - 7/9  и  - 4/9  получилось:  а)  -7/9 > - 4/5   б)  -7/9 =- 4/5  в)  -7/9< - 4/5

В2.    Разложите на множители:  а) 6ах² – 12ах³;  б) с – 16с³;  в) 3х² +5х + 2;

В3. В летнем лагере 172 ребенка и 24 воспитателя. В автобус помещается не более 30 пассажиров. Сколько автобусов требуется, чтобы перевезти всех из лагеря в город?

В4. На рисунке жирными точками показано суточное количество осадков, выпадавших в Казани с 3 по 15 февраля 1909 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько дней из данного периода выпадало более 3 миллиметров осадков.

 В5.  Чему равно значение выражения   при  а=.

В6. Для транспортировки 3 тонн груза на 50 км можно воспользоваться услугами одной из трех фирм-перевозчиков. Стоимость перевозки и грузоподъемность автомобилей для каждого перевозчика указана в таблице. Сколько рублей придется заплатить за самую дешевую перевозку?

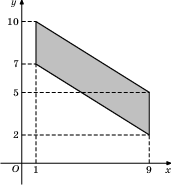
В7. Найдите площадь параллелограмма, вершины которого имеют координаты (1;7), (9;2), (9;5), (1;10).

В8. В прямоугольном треугольнике один из катетов равен 10, а угол, лежащий напротив него, равен . Найдите площадь треугольника.

В9. Баржа в 10:00 вышла из пункта А в пункт В, расположенный в 30 км от А. Пробыв в пункте В 1 час 40 минут, баржа отправилась назад и вернулась в пункт А в 21:00 того же дня. Определите (в км/ч) скорость течения реки, если известно, что собственная скорость баржи равна 7 км/ч.

В10. Какое из данных чисел не входит в область определения выражения   ?

                   1) 2;          2) 0;           3)  -4;           4) -2.

В11. Решите уравнение:   а) (х – 1) (5х - ) = 0.  б)

В12.    Решите неравенство:  а) 5х – 2(х-4) ≥ 9х + 23.

В13.    Найдите вершину параболы:   а) у = х² + 5х – 6.

В14. Запишите координаты точек пересечения графика функции                                                      у = 4х² + 8х – 5  с осью абсцисс.

В15.  Решите систему уравнений: .

             2.1.2 Задания к текущей аттестации

             Текущий контроль проводятся во время аудиторных занятий по математике в соответствии с учебным планом и рабочей программы ОДБ.07  «Математика» по всем разделам программы. Текущий контроль состоит из двух частей: теоретической и практической. При этом обучающиеся получают две отметки.

Теоретическая часть проходит в форме устных ответов: обучающиеся вытягивают пять карточек с вопросами, дают полный ответ (со списком вопросов обучающиеся знакомятся в начале изучения раздела).

Шкала перевода баллов в отметки по пятибалльной системе

Для выполнения контрольной работы дается два академических часа.

Критерии оценки контрольной работы

Отметка «5» если: работа выполнена полностью; в рассуждениях и обосновании решения нет пробелов и ошибок; (возможна одна неточ­ность, описка, не являющаяся следствием незнания или непо­нимания учебного материала).

 Отметка «4» если: работа выполнена полностью, но обоснования шагов решения; допущена одна ошибка или 2-3 недочета в выкладках, ри­сунках, чертежах или.

 Отметка «3» если: допущены более одной ошибки или более двух-трех недоче­тов в выкладках, чертежах или графиках, но учащийся владеет обязательными умениями по проверяемой теме. 

Отметка «2» если: допущены существенные ошибки, показавшие, что учащийся не владеет обязательными умениями по данной теме в полной мере. 

Показатели оценки: правильность решения задания, рациональность распределения времени на выполнение задания.

Тема «Основы тригонометрии. Тригонометрические функции»

Вопросы для повторения

1. Что называется радианом?

2. Как перевести градусную меру в радианную и, обратно, как перевести радианную меру угла в градусную?

3. Как определяются тригонометрические функции числового аргумента?

4. Какие знаки имеют тригонометрические функции в координатных четвертях?

5. Какие тригонометрические функции являются четными, а какие нечетными?

6. Что называется периодом функции? Какие периоды имеют тригонометрические функции?

7. Какими отношениями связаны тригонометрические функции одного и того же аргумента?

8. Сформулируйте формулы для синуса суммы и разности двух углов.

9. Сформулируйте формулы для косинуса суммы и разности двух углов.

10. Сформулируйте формулы для тангенса суммы и разности двух углов.

11. Сформулируйте формулы для котангенса суммы и разности двух углов.

12. Как выражаются тригонометрические функции двойных углов?

13. Как выражаются тригонометрические функции половинных углов?

14. По каким формулам преобразуются суммы и разности тригонометрических функций в произведение?

15. Сформулируйте формулы приведения.

16. Как построить графики тригонометрических функций?

17.Перечислите обратные тригонометрические функции, области определения и множества значений.

18. По каким формулам находятся решения простейших тригонометрических уравнений?

19. Какие методы решения тригонометрических уравнений вы знаете?

Контрольная работа «Основы тригонометрии. Тригонометрические функции»

Вариант 1

1.   Выберите верный ответ:

1.               Отношение абсциссы точки на окружности к длине радиуса называется………
А. …синусом угла        В …..косинусом угла    С….тангенсом угла        D…..котангенсом угла

2.               В какой четверти расположен угол 250˚?
A….I          B……II        C…..III      D……IV

3.               Найдите значение tg 30˚?
A                    B   1                  С             D   

4.               Какое из чисел меньше нуля.
A    sin140˚         B   cos140˚      C   sin50˚         D  cos50˚

5.               Углом, какой четверти является угол α, если sin α<0,  cosα<0.
A  I                 B   II                   C   III              D   IV

6.               Какое выражение не имеет смысла?
A     cos90 ˚           B   tg0˚          C   ctg90 ˚          D   tg90˚

7.                Вычислить, используя тригонометрический круг cos 210⁰
А               B -             C            D  -

2.   Упростить выражение:

a.                            1+sin² x + cos² x

b.                          

c.                            arctg  +arcsin (-1)

3.   Решите уравнение:

1.             cos x=

2.             sin

3.             2sin² x + 3sin x +1=0

4.2sin² x- 3sin x cos x+ cos² x=0

4.При движении автомобиля по дороге с поперечным уклоном возникает опасность его опрокидывания. Определить критический угол косогора, при достижении которого автомобиль может опрокинуться, если  tg β =  , где β – критический угол наклона ; В – расстояние между средними линиями колёс автомобиля, h – высота центра тяжести. В данной задаче  В =1.2 м , h = 0.6 м. Воспользоваться таблицами Брадиса.

Вариант  2

1.               Выберите верный ответ:

1.               Отношение ординаты точки на окружности к ее абсциссе называется…….
А……синусом угла.     В .косинусом угла.     С……тангенсом угла.     D. котангенсом угла.

2.               В какой четверти расположен угол 320˚
A   I                  B   II                 C    III          D    IV

3.               Найдите значение sin45˚
A                B  1                 C                        D     

4.               Какое из чисел больше нуля?
A  sin140˚         B cos140 ˚            C  sin250˚         D cos250˚

5.                Углом какой четверти является угол α, если sin α>0, cosα<0?
A   I                   B     II              C   III              D      IV

6.               .Какое из выражений не имеет смысла?
A cos0˚              B tg0 ˚              C  ctg0 ˚           D ctg90˚

1.   Вычислить, используя тригонометрический круг cos 1500
1)   1/2    2) - 1/2    3)   √3/2     4) - √3/2

2.               Упростить выражение:

a.               1- sin² x -  cos² x

b.              

c.               arcctg  +arccos  (-1)

3.      Решите  уравнение:

a.                cos x =

b.               sin

c.                2cos² x + 5cos x -3=0

d.               2sin² x + 3sin x cos x + cos² x=0

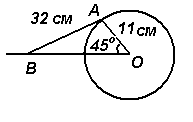
4. На рис. ниже показан кривошипно-шатунный механизм бензинового двигателя. Плечо ОА имеет длину 11 см и вращается по часовой стрелке вокруг О. Шатун АВ имеет длину 32 см, и конец В движется горизонтально. Определить угол между шатуном АВ и горизонталью и длину ОВ в положении, показанном на рис.

Тема «Степени и корни. Степенная функция»

Вопросы для повторения

1. Дайте определение возведения в степень числа с рациональным

2. Сформулируйте свойства возведения в степень с рациональным показателем.

3. Дайте определение операции по извлечению корня из числа.

4. Перечислите свойства арифметического корня.

5. Дайте определение степенной функции. Приведите примеры.

6. Сформулируйте свойства степенной функции. Приведите примеры.

7. Дайте определение показательной функции. Приведите примеры.

8. Сформулируйте свойства показательной функции. Приведите примеры.

9. Какие уравнения называются равносильными? Приведите примеры.

10. Какое уравнение называется следствием другого. Приведите примеры.

11. Какие методы преобразования уравнений вы знаете?

Контрольная работа «Степени и корни. Степенная функция»

Вариант 1

1.     Вычислите:

а)

б)

в)

г)

д)

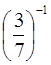
2. Упростите выражение:

а)

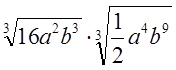
б)

в)

г)

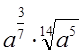
д)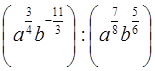

3. Постройте график функции

4. Расположите в порядке возрастания

5. Упростите выражение

6.Скорость автомобиля, разгоняющегося в местах старта по прямолинейному отрезку пути длиной l(в километрах) с постоянным ускорением а (в км/кв.ч), вычисляется по формуле

Определите наименьшее ускорение, с которым должен двигаться автомобиль, чтобы, проехав один километр, приобрести скорость не менее 100 км/ч. Ответ выразите в км/кв. ч.

Вариант 2

1.     Вычислите:

а)

б)

в)

г)

д)

2. Упростите выражение:

а)

б)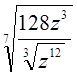

в)

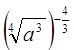
г)

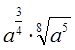
д)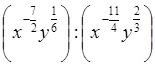 

3. Постройте график функции

4. Расположите в порядке возрастания

 , ,

5. Упростите выражение

6.Скорость автомобиля, разгоняющегося в местах старта по прямолинейному отрезку пути длиной l(в километрах) с постоянным ускорением а (в км/кв.ч), вычисляется по формуле

Определите наименьшее ускорение, с которым должен двигаться автомобиль, чтобы, проехав один километр, приобрести скорость не менее 120 км/ч. Ответ выразите в км/кв. ч.

Тема «Показательная функция»

Вопросы для повторения

1. Дайте определение показательной функции. Приведите примеры.

2.  Сформулируйте свойства показательной функции. Приведите примеры.

3. Приведите примеры графиков показательных функций.

4. Какие простейшие приемы решения показательных уравнений вы знаете?

5. Какие условия должны выполняться при решении показательных неравенств?

Контрольная работа «Показательная функция»

Вариант 1

А1. Какая функция является возрастающей?

1.      2.     3.     4.

А2. Найдите область значения функции 

1.. 2.. 3.. 4. .

А3. Решите уравнение

1. −2.       2.− 6.         3.2.           4.3.

А4. Решите неравенство .

1. .     2. .      3. .    4. .

А5. Определите наибольшее из чисел.

1.       2.      3. 1.     4..

В1. решите уравнение    

В2. решите неравенство

В3. Решите систему уравнений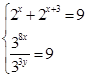

В4. Необходимо вычислить стоимость оборудования станции технического обслуживания через пять лет , если ее первоначальная стоимость ,

а ежегодный процесс амортизации равен 5,7%

Вариант2

А1. Какая функция является убывающей?

1.      2.      3.      4..

А2. Найдите область значения функции .

1.       2.     3.     4.

А3. Решите уравнение .

1.−2               2.4               3.2                    4.3

А4. Решите неравенство  .

1.      2.     3.     4.

А5. Определите наименьшее из чисел

1.           2.             3.           4.1

В1. Решите уравнение

В2. Решите неравенство

В3. Решите систему уравнений

В4. Стоимость оборудования автомастерской равна 500 тыс. р. Известно, что через x=10 лет стоимость этого оборудования вследствие амортизации будет равна B=200 тыс. р. Найдите процент ежегодной амортизации оборудования p, если стоимость оборудования через x лет находится по формуле:

В =

Тема «Логарифмы. Логарифмическая функция»

Вопросы для повторения

1. Дайте определение логарифмической функции. Приведите примеры.

2. Сформулируйте свойства логарифмической функции.

3. Сформулируйте определения логарифма числа. Какой логарифм называется десятичным? Какой логарифм называется натуральным?

4. Сформулируйте основное логарифмическое тождество.

5. Напишите свойства логарифмов.

6. Напишите формулу перехода к другому основанию.

7. В чем заключается суть метода потенцирования при решении логарифмических уравнений?

8. В чем заключается суть метода логарифмирования при решении логарифмических уравнений?

9. Какие условия должны выполняться при решении логарифмических неравенств?

Контрольная работа «Логарифмы. Логарифмическая функция»

Вариант 1

1. Вычислите:

а). ;      б). ;  в). ;  г). ;   д). ;

2. Постройте график функции: ;

3. Решите уравнение: ;

4. Решите систему уравнений: ;

5.Решите неравенство: .

6. Для обогрева помещения, температура в котором поддерживается на уровне  через радиатор отопления пропускают горячую воду. Расход проходящей через трубу радиатора воды  кг/с. Проходя по трубе расстояние x, вода охлаждается от начальной температуры  до температуры T, причём  где  — теплоёмкость воды,  — коэффициент теплообмена, а  — постоянная. Найдите, до какой температуры (в градусах Цельсия) охладится вода, если длина трубы радиатора равна 140 м.

Вариант 2.

1. Вычислите:

а). ;    б). ; в).;   г). ;    д). ;

2. Постройте график функции: ;

3. Решите уравнение: ;

4. Решите систему уравнений: ;

5.Решите неравенство: .

6.Ёмкость высоковольтного конденсатора в телевизоре  Ф. Параллельно с конденсатором подключeн резистор с сопротивлением  Ом. Во время работы телевизора напряжение на конденсаторе  кВ. После выключения телевизора напряжение на конденсаторе убывает до значения U (кВ) за время, определяемое выражением  (с), где  − постоянная. Определите напряжение на конденсаторе, если после выключения телевизора прошло 21 с. Ответ дайте в киловольтах.

Тема «Производная функции, ее применение»

Вопросы для повторения

1. Дайте определение производной функции.

2. Перечислите правила нахождения производной функции.

3. Какие функции называются дифференцируемыми?

4. Что называется угловым коэффициентом функции в данной точке?

5. Что называется касательной к линии в данной точке?

6. Чему равна производная постоянной?

7. Чему равна производная сложной функции?

8. Чему равна производная степенной функции?

9. Чему равна производная показательной функции?

10.Чему равна производная логарифмической функции

11. Чему равна производная синуса?

12. Чему равна производная косинуса?

13. Чему равна производная тангенса?

14. Дайте определения возрастания и убывания функции. Как найти промежутки монотонности с помощью производной?

15.  Дайте определение экстремума функции. Как найти точки экстремума с помощью производной?

16. Как найти наибольшее и наименьшее значения функции?

17. Сформулируйте общую схему исследования функции и построение графика.

     Контрольная работа «Производная функции, ее применение»

Вариант 1

1. Найдите производную функции в точке :

a)  ,  ;     б)  ;

в) ;    г)  , =4.

2. Используя формулу производной  суммы, найдите производную функции:

а) ;         б) .

3. Используя формулы производной произведения или частного, найдите производную функции:

а) ;   б)  .

4. Напишите уравнение касательной к графику функции      в  точке

5. Найдите точки экстремума функции и промежутки возрастания и убывания  f(x)=0,5.

6. Найдите наибольшее и наименьшее значения функции f(x)= 4x+, на отрезке [-1;0].

7. Исследовать функцию с помощью производной и построить ее график .

8. Закон прямолинейного движения задан уравнением s=-t3+9t2-24t-8. Найти

максимальную скорость движения тела (s- в метрах, t- в секундах).

9.Требуется изготовить поддон для слива отработанного ГСМ - открытую сверху коробку, вырезая по углам равные квадратики. Прямоугольный лист жести имеет длину 64 см и ширину 40 см. Каковы должны быть стороны вырезаемых квадратиков, чтобы вместимость поддона была максимальной.

Вариант 2

1. Найдите производную функции в точке :

a)  ,  ;     б)  ;

в) ;    г)  , =9.

2. Используя формулу производной  суммы, найдите производную функции:

а) ;         б) .

3. Используя формулы производной произведения или частного, найдите производную функции:

а) ;   б)  .

4. Напишите уравнение касательной к графику функции   y=   в  точке

5. Найдите точки экстремума функции и промежутки возрастания и убывания  f(x)=1,5.

6. Найдите наибольшее и наименьшее значения функции f(x)=  -, на отрезке [0;3].

7. Исследовать функцию с помощью производной и построить ее график .

8. Тело движется по закону s(t) =18t2+10t-2t3 (s- в метрах,t-в секундах). Найдите максимальную скорость движения тела.

9. Каким должно быть отношение диаметра основания к высоте закрытой

цилиндрической цистерны, чтобы при заданном объеме на изготовление цистерны шло как можно меньше материала?

Тема «Первообразная функции, ее применение»

Вопросы для повторения

1. Что называется первообразной? Перечислите свойства первообразной.

2. Что называется неопределенным интегралом?

3. Какие свойства неопределенного интеграла вы знаете?

4. Перечислите основные формулы интегрирования?

5. Какие методы интегрирования вы знаете?

6. В чем заключается суть формулы Ньютона-Лейбница?

7. Дайте определение определенного интеграла.

8. По какой формуле вычисляется площадь поверхности вращения?

9. По какой формуле вычисляется объем тела?

  Контрольная работа «Первообразная функции, ее применение»  

                                                         Вариант 1

 1. Найдите все первообразные функции .

 2. Найдите первообразную функции, график которой проходит через    точку с координатами (3;4).         

 3.  Для функции  найдите общий вид первообразных.

 4.Найдите площадь фигуры (предварительно сделайте рисунок), ограниченную:

1)    а=-1, b=2, f(x)=x+1 и осью Ох;

2)    Вычислите площадь фигуры, ограниченной линиями ; ;;.

     3) графиками функции y= осью ординат и y=1;

4) графиком функции y=, осью Ох и прямыми х =π/4, х = π/3.

                                                            Вариант 2

   1. Найдите все первообразные функции .

   2. Найдите первообразную функции, график которой проходит через точку с координатами (3;10).

   3. Для функции  найдите общий вид первообразных.

4.Найдите площадь фигуры (предварительно сделайте рисунок), ограниченную:

1) а=1,  b=3,  f(x)=x+4 и осью Ох;

2)графиками функции y= и y=1;

3)    Вычислите площадь фигуры, ограниченной линиями ; ;;.

4)  графиком функции y=, осью Ох и прямыми x=π/4, х = π/3

Тема «Уравнения и неравенства»

Вопросы для повторения

1. Какое уравнение называется линейным? Приведите пример.

2. Какое неравенство называется линейным? Приведите пример.

3. Что называется решением линейного уравнения и линейного неравенства?

4. Какие уравнения и системы уравнений называют равносильными?

5. Какие уравнения называют квадратными? Приведите пример.

6. При каких значениях дискриминанта квадратное уравнение имеет два различных решения, два совпадающих решения и не имеет решений?

7. Какие уравнения называются иррациональными?

8. Какие методы решения систем линейных уравнений вы знаете?

                          Контрольная работа «Уравнения и неравенства»

Вариант1

1.        Решите уравнение:

a.        (х²-1)⁶=(5-х)⁶

b.       х⁴-7х²+12=0

c.        3^2х-3∙3^х-54=0

d.   

          e. (х²-4)2-10(х²-4)+9=0

2.        Решите неравенство:

a.        100^2х+1≥0,1

b.   

            c. 

3.        Решите графически уравнение
3^х=4-х

4.        Применяя графический метод,

 определите, сколько решений имеет
 система уравнений:

    5. Решите систему неравенств:

    6. Решите системы уравнений:

a)   

7.     Ремонт одного и того же автомобиля Виктор и Алексей делают за 8 дней, как и Андрей вместе с Виктором, при этом Алексей с Андреем могут выполнить этот ремонт за 12 дней. Сколько дней длиться ремонт, если все три автомеханика будут работать одновременно?

8.     Коэффициент полезного действия (КПД) некоторого двигателя определяется формулой  где  − температура нагревателя (в градусах Кельвина),  − температура холодильника (в градусах Кельвина). При какой минимальной температуре нагревателя  КПД этого двигателя будет не меньше  если температура холодильника  К? Ответ выразите в градусах Кельвина.

Вариант2

1.     Решите уравнение:

a.      (х²-3х)⁸=(х-3)⁸

b.     х⁴-8х²-9=0

c.       2^2х+8∙2^х-9=0

 d.

    e. (x²-9)²-4(x²-9)+3=0

2.                 Решите неравенство:

a. 4^2х+3≤8^х-1

b.

      с. а) (x+5)(2x-1)(x-1)² ≤ 0

3.     Решите графически уравнение
                    2^х=3-х

4.     Применяя графический метод,

 определите, сколько решений имеет
 система уравнений:  

   5. Решите систему неравенств:

   6. Решите системы уравнений:

  7. Первые два часа автомобиль ехал со скоростью 95 км/ч, следующие два часа — со скоростью 45 км/ч, а затем один час — со скоростью 40 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

8. В боковой стенке высокого цилиндрического бака у самого дна закреплeн кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нeм, выраженная в метрах, меняется по закону  где t — время в секундах, прошедшее с момента открытия крана,  м — начальная высота столба воды,  — отношение площадей поперечных сечений крана и бака, а g — ускорение свободного падения (считайте  м/с). Через сколько секунд после открытия крана в баке останется четверть первоначального объeма воды?

Тема «Элементы комбинаторики, статистики и теории вероятностей»

Вопросы для повторения

1. «Комбинаторика – это…».

2. Какие множества называют упорядоченными?

3. Сформулируйте правило произведения.

4. Что называется перестановкой элементов множества? По какой формуле вычисляется число перестановок?

5. Что называется размещением? По какому правилу вычисляется число размещений?

6. Что называется сочетанием? По каким формулам вычисляется число сочетаний?

7. Перечислите свойства сочетаний.

8. Что такое треугольник Паскаля?

9. Напишите формулу бинома Ньютона.

10. Что называют опытом или испытанием?

11. Что называют событием, случайным, достоверным и невозможными событиями?

12. Какие события называют совместными и несовместными?

13. Какие события называют противоположными?

14. Что называют полной группой событий?

15. Сформулируйте теорему сложения для несовместных событий.

16. Сформулируйте теорему умножения для независимых событий.

17. Что называется условной вероятностью?

18. Напишите формулу полной вероятности.

19. Напишите формулу Байеса.

20. Напишите формулу Бернулли.

21. Что называется дискретной случайной величиной?

22. Что такое закон распределения дискретной случайной величины?

23. Перечислите характеристики дискретной случайной величины.

24. Что такое дисперсия случайной величины и среднее квадратичное отклонение.

Контрольная работа «Элементы комбинаторики, статистики и теории вероятностей» 

                                                                 Вариант 1

1.   Для каждого из этих событий определить, каким оно является: невозможным, достоверным или случайным.

а)     В результате броска игрального кубика появилось число 5.

б)    В результате броска игрального кубика появилось число больше 5.

в)     В результате броска игрального кубика появилось число меньше 7.

г)     Бросается игральный кубик 2 раза. Сумма выпавших чисел равна 13.

д)    При комнатной температуре и нормальном атмосферном давлении медь оказалась в жидком состоянии.

2.     Вычислить  

3.     Сколькими способами 4 человека могут разместиться на четырехместной скамейке?

4.     Вычислить 

5.     Сколько существует четырехзначных номеров, не содержащих цифр 0, 7, 8?

6.     Вычислить

7.     В классе изучают 8 предметов естественно-научного цикла. Сколькими способами можно составить расписание на пятницу, если в этот день должны быть 5 уроков из пяти разных предметов?

8.     а) В ящике 250 яиц, из которых 20 бракованных. Какова вероятность, что первое взятое из корзины яйцо не окажется бракованным?

б) Из 30 учеников спорткласса, 11 занимается футболом, 6 – волейболом, 8 – бегом, а остальные прыжками в длину. Какова вероятность того, что один произвольно выбранный ученик класса занимается игровым видом спорта?

     в) Какова вероятность, что ребенок родится 7 числа?

9.     Дан ряд чисел:

110; 120; 125; 130; 140; 125; 120; 130; 125; 130; 110; 120; 125; 125.

Укажите моду, медиану, размах, среднее арифметическое ряда чисел. Составьте таблицу распределения по частотам. Изобразить многоугольник распределения.

   10.Электронный прибор содержит 2 микросхемы. Вероятность выхода из строя первой микросхемы в течение определенного (достаточно большого) времени равна 0,2, а второй – 0,1. Известно, что из строя вышла одна микросхема. Какова вероятность того, что это первая микросхема?

                                                             Вариант 2

1.     Для каждого из этих событий определить, каким оно является: невозможным, достоверным или случайным.

а)     В результате броска игрального кубика появилось число 6.

б)    В результате броска игрального кубика появилось число больше 4.

в)     В результате броска игрального кубика появилось число меньше 8.

г)     Бросается игральный кубик 2 раза. Сумма выпавших чисел равна 17.

д)    При комнатной температуре и нормальном атмосферном давлении вода оказалась в жидком состоянии.

2.     Вычислить

3.     Курьер должен разнести пакеты в 7 различных учреждений. Сколько маршрутов он может выбрать?

4.     Вычислить

5.     Из 30 учеников необходимо выбрать председателя и секретаря. Сколькими способами это можно сделать?

6.     Вычислить  

      7.  Сколько существует различных двузначных чисел, в записи которых можно использовать цифры 1, 2, 3, 4, 5, 6, если цифры в числе должны быть различными?

      8. а) Бросают две игральные кости. Найдите вероятность того, что сумма выпавших очков равна 5;

           б) На витрине магазина стоит 96 упаковок йогурта, из них 21 – с клубничной начинкой, 31 – с малиновой, 15 – с банановой. Артем взял наудачу 1 упаковку йогурта. Какова вероятность того, что это йогурт с клубничной или банановой начинкой?

      в) Какова вероятность того, что выбранное двузначное число делится  на 12?

9. Дан ряд чисел:

11; 12; 23; 11; 15; 25; 12; 11; 23; 15.

Укажите моду, медиану, размах, среднее арифметическое ряда чисел. Составьте таблицу распределения по частотам. Изобразить многоугольник распределения.

    10. Имеется 20 блоков одинаковых деталей. Вероятность того, что в одном взятом наудачу блоке детали окажутся стандартными, равна 0,75. Найти наивероятнейшее число блоков, в которых все детали стандартные.

Тема «Прямые и плоскости в пространстве»

    Вопросы для повторения

1. Перечислите основные фигуры в пространстве.

2. Аксиомы стереометрии; следствия из аксиом.

3. Перечислите способы задания плоскости.

4. Признак параллельности двух прямых.

5. Признак параллельности прямой и плоскости.

6. Признак скрещивающихся прямых.

7. Раскройте понятие «угол между прямыми».

8. Сформулируйте определение двуграного угла.

9. Сформулируйте определение трехграного угла.

10. Перечислите взаимное расположение двух прямых в пространстве

11. Какие прямые называются параллельными в пространстве?

12. Какие прямые называются скрещивающимися в пространстве?

13. Какие прямые называются перпендикулярными в пространстве?

14. Перечислите взаимное расположение прямой и плоскости в пространстве.

15. Раскройте понятие «угол между прямой и плоскостью».

16.Раскройте понятие «параллельность прямой и плоскости».

17. Раскройте понятие «перпендикулярность прямой и плоскости».

18. Перечислите взаимное расположение двух плоскостей в пространстве.

19. Раскройте понятие «угол между плоскостями».

20. Раскройте понятие «параллельность плоскостей».

21. Раскройте понятие «перпендикулярность плоскостей».

22. Как найти расстояние от точки до прямой?

23. Как найти расстояние между прямыми?

24. Как найти расстояние между плоскостями?

25. Продолжите определение: «Перпендикуляр – это…».

26. Продолжите определение: «Наклонная – это…».

27. Продолжите определение: «Проекция наклонной – это…».

28. Перечислите свойства параллельного проектирования.

29.Приведите примеры симметрий на плоскости в природе, искусстве, архитектуре.

Контрольная работа «Прямые и плоскости в пространстве»

Вариант 1

1.     Постройте чертеж по условию:

a) Прямая АВ пересекает плоскость α в точке М.

b)       Прямые MB и МС пересекают плоскость β в разных точках.

c)    a  β,  M a,  a ⊥RM. Покажите несколько способов расположения прямой RM.

d) 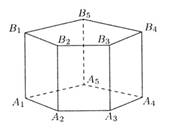        a ∥ b,   c ⊥a

2. По чертежу ответьте на вопросы:

a)     Назовите параллельные прямые;

b)    Назовите параллельные плоскости;

c)     Назовите плоскости и  параллельные им прямые;

d)    Назовите пересекающиеся прямые;

e)     Назовите скрещивающиеся прямые;

3.     Из точки к плоскости проведены перпендикуляр и наклонная, длина перпендикуляра равна 12 см, длина наклонной 13 см. Найдите:

a)      проекцию наклонной на эту плоскость;

b)    угол между наклонной и плоскостью.

4.     Опишите способ взаимного расположения прямой и плоскости в пространстве.

5.    Плоскость  a  пересекает  стороны  AB  и  BC  треугольника  ABC

соответственно  в  точках  D  и  E,  причем  AC||a.  Найдите  AC,  если  BD:AD=3:2  и  DE=9 см.  

6. В прямоугольном параллелепипеде ABCDABCD дано: АВ=ВС=см., ВD=12 см.

 Найдите: а) расстояние между прямыми ВD и АА; 

б) угол между прямой ВDи плоскостью ABC.  

Вариант 2

1.  Постройте чертеж по условию:

a)                Прямая АВ не  пересекает плоскость α.

b)       Прямые MB и МС пересекают плоскость β в одной и той же точке

c)    К ∉ β,   а  β,   КМ ∩ а = М,   b∥ KM . Покажите несколько способов расположения прямой b.

d) 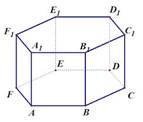      a ⊥ b,   c ⊥ b

2.     По чертежу ответьте на вопросы:

a)            Назовите параллельные прямые;

b)           Назовите параллельные плоскости;

c)            Назовите плоскости и  параллельные им прямые;

d)           Назовите пересекающиеся прямые;

e)            Назовите скрещивающиеся прямые;

3.     Из точки к плоскости проведены перпендикуляр и наклонная, длина перпендикуляра равна 4 см, длина наклонной 5 см. Найдите:

a)      проекцию наклонной на эту плоскость;

b)    угол между наклонной и плоскостью.

4.     Опишите способ взаимного расположения двух прямых в пространстве.

     5.    Плоскость  a  пересекает  стороны  AB  и  BC  треугольника  ABC

соответственно  в  точках  D  и  E,  причем  AC||a.  Найдите  AC,  если  BD:AD=5:4  и  DE=10 см.

    6. В прямоугольном параллелепипеде ABCDABCD дано: АВ=ВС=см., ВD=20 см. 

     Найдите: а) расстояние между прямыми ВD и АА; 

     б) угол между прямой ВDи плоскостью ABC.  

Тема «Координаты и векторы в пространстве»

Вопросы для повторения

1. Из чего состоит прямоугольная система координат в пространстве?

2. Раскройте понятие «вектор».

3. Перечислите и раскройте правила сложения векторов.

4. Какие векторы называются коллинеарными?

5. Какие векторы называются компланарными?

6. Как найти координаты вектора?

7. Чему равна длина вектора?

8. Чему равно скалярное произведение векторов?

9. Чему равен угол между векторами?

Контрольная работа «Координаты и векторы в пространстве».

Вариант 1

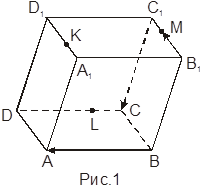1.  а) Сформулируйте понятие коллинеарных векторов;

На рис.1 изображен параллелепипед. Выпишете:

б) 5 векторов, противоположно направленных к ;

в) 5 векторов, сонаправленных с ;

г) 2 вектора, равных .

2.     Нарисуйте тетраэдр DABC. Изобразите на рисунке векторы:

а) ; б) ; в) .

3. 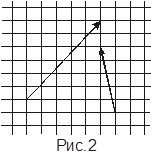    Скопируйте векторы с рис. 2 в тетрадь и постройте векторы:

а) ; б) ; в) ; г) .

4.     Упростите выражения:

           а) ;  

           б) ;

           в) .

5.     Дан параллелепипед ABCDA₁B₁C₁D₁ (рис.1). Какие из трех следующих векторов компланарны: а) ;                           б) ; в) ; г) ?

6.     Найдите  координаты  вектора  , если    А(5; -1; 3), В(2; -2; 4).

Вариант 2

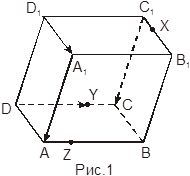
1.     На рис.1 изображен параллелепипед. Выпишете:

а) 5 векторов, сонаправленных с ;

б) 5 векторов, противоположно направленных к ;

в) Сформулируйте понятие равных векторов;

г) 2 вектора, равных .

2.     Нарисуйте тетраэдр DABC. Изобразите на рисунке векторы:

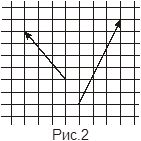а) ; б) ; в) .

3.     Скопируйте векторы с рис. 2 в тетрадь и постройте векторы:

а) ; б) ; в) ; г) .

4.     Упростите выражения: а) ;

 б);   

в).

5.     Дан параллелепипед ABCDA₁B₁C₁D₁ (рис.1). Какие из трех следующих векторов компланарны: а) ; б) ;  в) ; г) ?

6.     Найдите координаты вектора  , если  А(6; 3; -2), В(2; 4; -5).

Тема «Многогранники и тела вращения»

Вопросы для повторения

1. Что называется многогранником?

2. Что называется многогранной поверхностью?

3. Какой многогранник называют выпуклым?

4. Что называют призмой? Дайте определение граням, ребрам и вершинам призмы.

5. Что называется параллелепипедом?

6. Сформулируйте теорему о диагоналях прямоугольного параллелепипеда.

7. Чему равна боковая и полная поверхность призмы?

8. Что называется пирамидой? Дайте определение апофемы пирамиды.

9. Чему равны боковая и полная поверхность пирамиды?

10. Что называется усеченной пирамидой?

11. Чему равны боковая и полная поверхность усеченной пирамиды?

12. Какой многогранник называется правильным?

13. Перечислите все правильные многогранники. Сколько каждый из них имеет граней, ребер и вершин?

14. Дайте определение тела вращения.

15. Дайте определение цилиндра.

16. Чему равны боковая и полная поверхности цилиндра?

17. Дайте определение конуса.

18. Чему равны боковая и полная поверхности конуса?

19. Дайте определение усеченного конуса.

20. Чему равны боковая и полная поверхности усеченного конуса?

21. Дайте определение сферы.

22. Дайте определение шара.

23. Какими фигурами являются сечения сферы и шара?

24. Какая фигура получается при вращении кругового сектора?

25. Что называется шаровым поясом?

26. Какие требования предъявляются к понятию объема тела?

27. По какой формуле вычисляется объемы призмы, прямоугольного параллелепипеда, куба?

28. Сформулируйте теорему об объеме пирамиды.

29. По какой формуле вычисляется объем усеченной пирамиды?

30. Сформулируйте теорему об объеме прямого кругового цилиндра.

31. Сформулируйте теорему об объеме конуса.

32. По какой формуле вычисляется объем усеченного конуса?

33. Сформулируйте теорему об объеме шара.

34. По какой формуле находится объем шарового сегмента?

35. По какой формуле находится объем шарового сектора?

   Контрольная работа «Многогранники и тела вращения»

Вариант 1

1. Основание прямой призмы - прямоугольный треугольник с катетами 6 и 8 см. Найдите площадь боковой поверхности призмы, если ее наибольшая боковая грань - квадрат.

2.  Боковое ребро правильной четырехугольной пирамиды равно 4 см и образует с плоскостью основания пирамиды угол 45°.

а) Найдите высоту пирамиды.

б) Найдите площадь боковой поверхности пирамиды.

       3. Высота цилиндра 8 дм, радиус основания 5 дм. Цилиндр пересечен плоскостью параллельно оси так, что в сечении получился квадрат. Найдите расстояние от этого сечения до оси цилиндра.

       4.  Радиус сферы равен 15 см. Найдите длину окружности сечения, удаленного от центра сферы на 12 см.

       5.  Основанием прямой призмы является ромб со стороной 12 см и углом 60⁰. Меньшее из диагональных сечений призмы является квадратом. Найдите объем призмы.

         6. Бак в форме правильной четырехугольной пирамиды вмещает 190 л бензи­на. Найти глубину этого бака, если стороны оснований 60 и 40 см.

Вариант 2

1.  Основание прямой призмы - прямоугольный треугольник с гипотенузой 13 см и катетом 12 см. Найдите площадь боковой поверхности призмы, если ее наименьшая боковая грань - квадрат.

2.  Высота правильной четырехугольной пирамиды равна √6 см, а боковое ребро наклонено к плоскости основания под углом 60°.

а) Найдите боковое ребро пирамиды.

б) Найдите площадь боковой поверхности пирамиды.  

3.   Радиус шара равен 17 см. Найдите площадь сечения шара, удаленного от его центра на 15 см.

4.   Радиус основания конуса равен 3 м, а высота 4 м. Найдите образующую и площадь осевого сечения.

5. Осевым сечением цилиндра является квадрат, диагональ которого равна см. Найдите объем цилиндра.

6. Сколько тонн бензина можно хранить в цистерне цилиндрической формы, если ее диаметр 5 м, длина 3 м, а плотность бензина 0,7 г/м?

2.1.1 Задания к промежуточной аттестации по учебной дисциплине ОДБ.07 «Математика» в форме экзамена в четвертом семестре на втором курсе

Вариант 1

Часть 1

Ответом к заданиям В1–В 12 является целое число или конечная десятичная  дробь. Единицы измерений писать не нужно.

В1. Найдите значение выражения

В2. Найдите значение выражения ;

В3. В городе 180 000 жителей, причем 30 % - это пенсионеры. Сколько пенсионеров в этом городе?

В4. Площадь трапеции вычисляется по формуле S =, где   a и b – основания трапеции, h – её высота. Пользуясь этой формулой, найдите S, если a=3, b=8 и h=4.

В5. На день рождения полагается дарить букет из нечетного числа цветов. Хризантемы стоят 50 рублей за штуку. У Вани есть 510 рублей. Из какого наибольшего числа хризантем он может купить букет Маше на день рождения?

В6. Найдите корень уравнения .

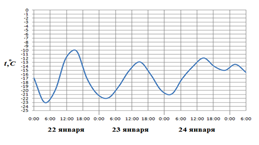
В7. На рисунке показано изменение температуры воздуха на протяжении трех суток. По горизонтали указывается дата и время суток, по вертикали — значение температуры в градусах Цельсия. Определите по рисунку разность между наибольшей и наименьшей температурами воздуха 22 января.

В8. Рейтинговое агентство определяет рейтинг соотношения «цена-качество» микроволновых печей. Рейтинг вычисляется на основе средней цены P  и оценок функциональности F, качества Q  и дизайна D . Каждый отдельный показатель оценивается экспертами по 5-балльной шкале целыми числами от 0 до 4. Итоговый рейтинг вычисляется по формуле

R=8(F+Q)+4D-0,01P

В таблице даны оценки каждого показателя для нескольких моделей печей. Определите, какая модель имеет наивысший рейтинг. В ответ запишите значение этого рейтинга.

В9. На экзамен вынесено 50 вопросов, Андрей не выучил 5 из них. Найдите вероятность того, что ему попадется выученный вопрос.

В10. Объем конуса равен 9π , а его высота равна 3. Найдите радиус основания конуса.

В11. В треугольнике АВС  угол С равен 90°, АС = 12,
АB = 20, Найдите sinA.

В12.На рисунке изображен график  — производной функции , определенной на интервале . Найдите количество точек максимума функции , принадлежащих отрезку .

Часть II

Запишите сначала номер выполняемого задания (С1,С2, и т. д.), а затем полное обоснованное решение и ответ. Ответы записывайте чётко и разборчиво.

С1. Найдите , если =0,8 и .

С2.Расстояние между городами A и B равно 150 км. Из города A в город B выехал автомобиль, а через 30 минут следом за ним со скоростью 90 км/ч выехал мотоциклист, догнал автомобиль в городе C и повернул обратно. Когда он вернулся в A, автомобиль прибыл в B. Найдите расстояние от A до C. Ответ дайте в километрах.

С3.Найдите промежутки возрастания и убывания функции и определите её точки экстремума f(x)=;

С4. а) Решить уравнение 2cos2x + 4 cos (-x)+1=0;

б) Найдите все корни этого уравнения, принадлежащие промежутку [- -].

С5. Вычислить, предварительно сделав рисунок, площадь фигуры, ограниченной линиями: .

С6.Решите неравенство

С7. Сторона основания правильной треугольной призмы  равна 4, а высота этой призмы равна 3. Найдите площадь полной поверхности призмы .

Вариант 2

Часть 1

Ответом к заданиям В1–В 12 является целое число или конечная десятичная дробь. Единицы измерений писать не нужно.

В1. Найдите значение выражения  ;

В2. Найдите значение выражения   ;

В3. Только 90% из 30 000 выпускников города правильно решили задачу № 1. Сколько выпускников из этого города правильно решили задачу №  1?

В4. Найдите m из равенства F=m, если F=84 иa=12.

В5. На день рождения полагается дарить букет из нечетного числа цветов. Чайные розы стоят 40 рублей за штуку. У Вани есть 190 рублей. Из какого наибольшего числа роз он может купить букет Маше на день рождения?

В6.  Найдите корень уравнения

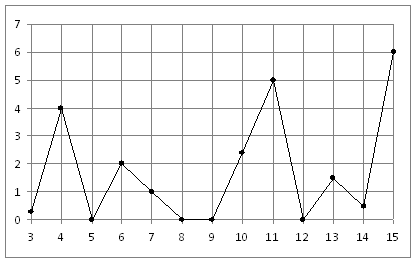
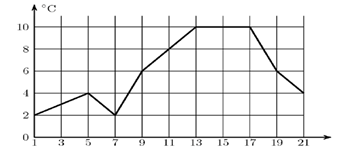
В7.  Первый посев семян петрушки рекомендуется проводить в апреле при дневной температуре воздуха не менее +6⁰ С. На рисунке показан прогноз дневной температуры воздуха в первых трех неделях апреля. Определите, в течение скольких дней за этот период можно производить посев петрушки.

В8. Рейтинговое агентство определяет рейтинг соотношения «цена-качество» микроволновых печей. Рейтинг вычисляется на основе средней цены P  и оценок функциональности F, качества Q  и дизайна D . Каждый отдельный показатель оценивается экспертами по 5-балльной шкале целыми числами от 0 до 4. Итоговый рейтинг вычисляется по формуле

R=8(F+Q)+4D-0,01P

В таблице даны оценки каждого показателя для нескольких моделей печей. Определите, какая модель имеет наивысший рейтинг. В ответ запишите значение этого рейтинга.

В 9.На экзамен вынесено 50 вопросов, Алексей не выучил 5 из них. Найдите вероятность того, что ему попадется  не выученный вопрос.

В10. Радиус основания цилиндра равен 3, высота равна 2. Найдите объем цилиндра, деленный  на  π.

В11. В треугольнике АВС угол  Сравен 90°, АВ =10
АС =. Найдите sin

 В12.На рисунке изображён график  — производной функции , определенной на интервале . В какой точке отрезка функция  принимает наибольшее значение?

II часть

Запишите сначала номер выполняемого задания (С1,С2, и т. д.), а затем полное обоснованное решение и ответ. Ответы записывайте чётко и разборчиво.

С1. Найдите , если =;;

С2.Весной катер идёт против течения реки в 1 2/3 раза медленнее, чем по течению. Летом течение становится на 1 км/ч медленнее. Поэтому летом катер идёт против течения в 1 1/2 раза медленнее, чем по течению. Найдите скорость течения весной (в км/ч).

С3.Найдите промежутки возрастания и убывания функции и определите её точки экстремума  f(x)=3;

С4. а) Решить уравнение sinx =;

б) Найдите все корни этого уравнения, принадлежащие промежутку [- -].

С5. Вычислить, предварительно сделав рисунок, площадь фигуры, ограниченной линиями:  ,осью Ох.

С6.Решите неравенство

С7. В прямоугольном параллелепипеде ребра CD, CB и диагональ боковой грани  равны соответственно 3, 4 и 5. Найдите площадь боковой поверхности параллелепипеда .

Вариант 3

Часть 1

Ответом к заданиям В1–В 12 является целое число или конечная десятичная  дробь. Единицы измерений писать не нужно.

^{В1. Вычислите значение выражения}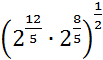

^В2. Найдите значение выражения    

В3.В сентябре 1 кг слив стоил 75 рублей. В октябре сливы подорожали на 40%. Сколько рублей стоил 1 кг слив после подорожания в октябре?

В4. Площадь треугольника вычисляется по формуле S=1/2bcsinα, где b и c — две стороны треугольника, а α — угол между ними. Пользуясь этой формулой, найдите площадь S, если b=18, c=16 и sinα=13.

В5. Для ремонта требуется 57 рулонов обоев. Какое наименьшее количество пачек обойного клея нужно для такого ремонта, если 1 пачка клея рассчитана на 5 рулонов?

В6.Решите уравнение .

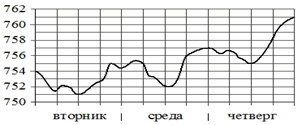
В 7. На рисунке изображён график значений атмосферного давления в некотором городе за три дня. По горизонтали указаны дни недели, по вертикали — значения атмосферного давления в миллиметрах ртутного столба.Определите по рисунку наименьшее значение атмосферного давления 
за данные три дня (в миллиметрах ртутного столба).

В8.Строительный подрядчик планирует купить 20 тонн облицовочного кирпича у одного из трёх поставщиков. Один кирпич весит 5 кг. Цена кирпича 
и условия доставки всей покупки приведены в таблице.

Во сколько рублей обойдётся наиболее дешёвый вариант покупки с доставкой?

В9. В среднем из 500 садовых насосов, поступивших в продажу, 25 подтекает. Найдите вероятность того, что случайно выбранный для контроля насос подтекает.

В 10.Объём конуса равен 25π, а его высота равна 3. Найдите радиус основания конуса.

   В 11. В треугольнике АВС угол С равен 90°, АВ =10, ВС =6. Найдите sin

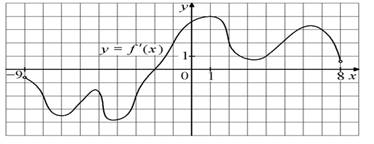
В12. На рисунке изображён график y=f′(x) — производной функции f(x), определённой на интервале (−9; 8). Найдите точку экстремума функции f(x) на отрезке [−3; 3].

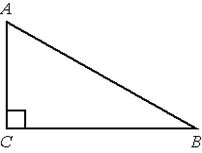
II часть

Запишите сначала номер выполняемого задания (С1, С2, и т. д.), а затем полное обоснованное решение и ответ. Ответы записывайте чётко и разборчиво.

С1 Найдите значение , если известно, что   и   <<

С2. Из пункта А в пункт В, расстояние между которыми 75 км, одновременно выехали автомобилист и велосипедист. Известно, что за час автомобилист проезжает на 40 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 6 часов позже автомобилиста. Ответ дайте в км/ч.

С3. Напишите уравнение касательной к графику функции      

в точке с абсциссой     

С4.а) Решите уравнение cos2x+ =0,75.

б) Найдите все корни этого уравнения, принадлежащие отрезку [π; 5π/2].

С5. Найдите площадь фигуры, ограниченной линиями у = 3х², у = 0,  х =  1 , х = 3.

С6. Решите неравенство  .

С7.ABCDA₁B₁C₁D₁ – прямоугольный параллелепипед, стороны основания которого 10 см и 15 см, а его боковое ребро равно 6 см. Найти   параллелепипеда.

Вариант 4

Часть 1

Ответом к заданиям В1–В 12 является целое число или конечная десятичная дробь. Единицы измерений писать не нужно.

В1. Вычислите значение выражения.

В2. ^{Вычислите значение выражения}

В3. Городской бюджет составляет 67 млн рублей, а расходы на одну из его статей составили 15%. Сколько миллионов рублей потрачено на эту статью бюджета?

В4.В фирме «Родник» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле C=6000+4100n, где n — число колец, установленных при копании колодца. Пользуясь этой формулой, рассчитайте стоимость колодца из 4 колец. Ответ дайте в рублях.

В5. Шоколадка стоит 31 рубль. В воскресенье в супермаркете действует специальное предложение: заплатив за две шоколадки, покупатель получает три (одну в подарок). Сколько шоколадок можно получить на 170 рублей в воскресенье?

В6. Решите уравнение   .

В7. На диаграмме показана среднемесячная температура воздуха 
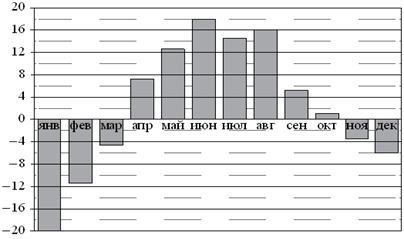
в Екатеринбурге (Свердловске) за каждый месяц 1973 года. По горизонтали указываются месяцы, по вертикали —температура в градусах Цельсия. Определите по диаграмме наибольшую среднемесячную температуру во второй половине 1973 года. Ответ дайте в градусах Цельсия.

.

В8. Для транспортировки 40 тонн груза на 1000 км можно воспользоваться услугами одной из трёх фирм-перевозчиков. Стоимость перевозки и грузоподъёмность автомобилей каждого перевозчика указаны в таблице. Во сколько рублей обойдётся наиболее дешёвый вариант перевозки.

В9. На семинар приехали 7 учёных из Норвегии, 7 из России и 6 из Испании. Каждый учёный подготовил один доклад. Порядок докладов определяется случайным образом. Найдите вероятность того, что восьмым окажется доклад учёного из России.

В10. Даны два цилиндра. Радиус основания и высота первого цилиндра равны соответственно 2 и 6, а второго — 6 и 4. Во сколько раз объём второго цилиндра больше объёма первого?

В11.

На стороне BC прямоугольника ABCD, у которого AB=12 и AD=17, отмечена точка E так, что треугольник ABE равнобедренный. Найдите ED.

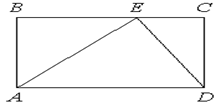
В12. На рисунке изображён график функции y=f′(x) — производной функции f(x), определённой на интервале (− 3 ; 8). Найдите точку минимума функции f(x).

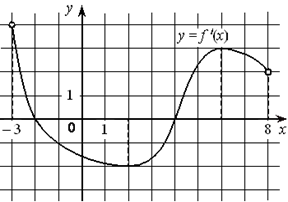
II часть

Запишите сначала номер выполняемого задания (С1, С2, и т. д.), а затем полное обоснованное решение и ответ. Ответы записывайте чётко и разборчиво.

С1 Найдите значение, если известно, что и 0<<π/2.

С2.Два велосипедиста одновременно отправились в 88-километровый пробег. Первый ехал со скоростью, на 3 км/ч большей, чем скорость второго, и прибыл к финишу на 3 часа раньше второго. Найти скорость велосипедиста, пришедшего к финишу вторым. Ответ дайте в км/ч.

С3. Найдите наименьшее значение функции y=x3−x2−8x+4 на отрезке [1; 7].

С4.а)Решите уравнение sin2x=sinx−2cosx+1.

б) Укажите корни этого уравнения, принадлежащие отрезку [3π/2; 3π].

С5. Найдите площадь фигуры (предварительно сделайте рисунок), ограниченную:

 а=1, b=3, f(x)=x+4 и осью Ох.

С6. Решите систему уравнений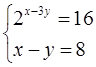

С7. Найдите объём правильной четырёхугольной пирамиды, сторона основания которой равна 8 см, а боковое ребро равно .

Эталон ответов

1 вариант

2 вариант

3 вариант

4 вариант

Шкала оценки образовательных достижений

Каждое из заданий В1–В12 считается выполненными верно, если экзаменуемый дал верный ответ в виде целого числа или конечной десятичной дроби. Каждое верно выполненное задание оценивается 1 баллом.

Количество баллов, выставленных за выполнение заданий С1–С7, зависит от полноты решения и правильности ответа.

Общие требования к выполнению заданий с развёрнутым ответом: решение должно быть математически грамотным, полным, все возможные случаи должны быть рассмотрены. Методы решения, формы его записи иформы записи ответа могут быть разными. За решение, в котором обоснованно получен правильный ответ, выставляется максимальное количество баллов. Правильный ответ при отсутствии текста решения оценивается в 0 баллов.

Перечень материалов, оборудования и информационных источников, используемых в аттестации

Основные источники:

1. Алимов Ш.А., Колягин Ю.М., Ткачева М.В. и др. Алгебра и начала математического анализа (базовый уровень) 10-11 Просвещение, 2020 г.

2. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия (базовый и профильный уровни) 10-11 Просвещение, 2020 г.

3. Гущин Д.Д., Малышев А.В. ЕГЭ 2020. Задачи прикладного содержания. – М.:МЦНМО, 2020 г.

Интернет ресурсы:

1.     www.mathematics.ru

2. http://ege.edu.ru;

3.http://www.fipi.ru.

 4.http://www.itmathrepetitor.ru

Лист согласования

Дополнения и изменения к комплекту КОС на учебный год

Дополнения и изменения к комплекту КОСна __________ учебный год по дисциплине _________________________________________________________________ 

В комплект КОС внесены следующие изменения:

____________________________________________________________________________

____________________________________________________________________________

____________________________________________________________________________

____________________________________________________________________________

____________________________________________________________________________

Дополнения и изменения в комплекте КОС обсуждены на заседании ЦМК _______________________________________________________

«_____» ____________ 20_____г. (протокол № _______ ). 

Председатель  ЦМК ________________ /___________________/

Скачано с www.znanio.ru