кругов Эйлера -Венна_ Тренировочные упражнения _Приложение 1

Тренировочные упражнения                                          Приложение 1

1.С помощью кругов Эйлера-Венна  покажите, что множество натуральных чисел  является подмножеством целых чисел. Запишите с помощью условных обозначений.

2.А) Покажите на диаграмме Эйлера-Венна множество целых чисел А,  которые  больше -5, но меньше 5.

Б) Запишите перечислением элементов множество натуральных чисел В,

которые меньше 5.

В) В каком соотношении находятся множества А и В? Обозначьте их.

3.А)Обозначьте через А множество целых однозначных чисел. Запишите множество А перечислением его элементов.

Б) Обозначьте через В множество натуральных однозначных чисел. Запишите множество В перечислением его элементов.

В) Изобразите с помощью кругов Эйлера-Венна соотношение между этими множествами.

4. Выберите из чисел 5;-7;0;;-3,7;8,6;-125;324;;-;-2;35;13;65;-79;976:

1) натуральные;                                 4) неположительные;

2) целые;                                             5) целые отрицательные;

3) положительные;                           6) дробные неотрицательные.

5. Запишите шесть целых чисел, которые не являются натуральными.

6.Верно ли утверждение:

1) положительное число;                   6)-4- рациональное число;

2) рациональное число;                     7) 0-натуральное число;

3) -4- отрицательное число;                       8)0- целое число;

4)-4-натуральное число;                             9) 0 –рациональное число;

5) -4- целое число;                                      10)0-положительное число.

Если элементы множества являются только числа, то его называют числовым.

Приведем примеры числовых множеств.

·         Множество натуральных чисел. Обозначают буквой  N.

·          Множество целых чисел. Обозначают буквой  Z.

·         Множество рациональных чисел. Обозначают буквой  Q.

Обратите внимание: все элементы множества N являются элементами множества Z .

В таких случаях говорят, что множество N является подмножеством множества Z.

Записывают (читают - подмножество Z). Понятно, что .

Наглядно это можно изобразить с помощью кругов Эйлера-Венна.

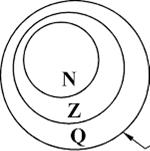  Числовые множества на кругах Эйлера-Венна.

Иногда нужно рассматривать множества, в котором нет ни одного элемента. Такое множество называют пустым. Обозначают Ø. Например, множество твоих одноклассников, побывавших на Луне- пока еще пустое множество.

Пустое множество является подмножеством любого множества.

Используемая литература:

1.Т.А. Алдамуратова Математика 6 класс, Атамура, Алматы,2006, 2-е издани

2.http://11book.ru/6-klass/150-matematika/2370-matematika-6-klass-merzlyak

Скачано с www.znanio.ru