ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ И НАУКИ БРЯНСКОЙ ОБЛАСТИ Государственное автономное профессиональное образовательное учреждение «Брянский строительно-технологический техникум имени Л.Я. Кучеева»
	Методические рекомендации по выполнению лабораторных работ по физике

 

 

 

 

 

 

 

Методические рекомендации

по выполнению лабораторных работ по физике для I курса

ОУД.П.10 Физика

по профессиям: 

 

                   08.01.06 Мастер сухого строительства

                   08.01.07 Мастер общестроительных работ

                   08.01.25 Мастер отделочных строительных и декоративных работ

                  

                  

 

 

 

 

Брянск, 2021

Содержание

Пояснительная записка. 3

Лабораторная работа № 1

Сохранение механической энергии при движении тела под действием сил тяжести и упругости  5

Лабораторная работа № 2

Изучение особенностей силы трения (скольжения) 8

Лабораторная работа № 3

Исследование движения тела под действием постоянной силы.. 10

Лабораторная работа № 4

Изучение закона сохранения импульса. 13

Лабораторная работа № 5

Сравнение работы силы с изменением кинетической энергии тела. 19

Лабораторная работа № 6

Изучение зависимости периода колебаний нитяного маятника от длины нити. 20

Лабораторная работа №7

Измерение влажности воздуха. 21

Лабораторная работа №8

Измерение поверхностного жидкости. 22

Лабораторная работа №9

Наблюдение кристаллизации. Изучение деформации растяжения. 24

Лабораторная работа №10

Изучение теплового расширения твердых тел. 26

Лабораторная работа №11

Изучение особенностей теплового расширения воды.. 27

Список использованной литературы.. 29

 

 

 

 

 

 

 

Пояснительная записка

 

Предлагаемые методические рекомендации входят в учебно-методический комплекс по дисциплине «Физика», разработаны для студентов первого и второго курсов.

Предлагаемые методические указания представляют собой практикум по лабораторным работам для обучающихся по всему курсу общей.

Основная цель пособия – способствовать формированию у обучающихся ключевых учебных и личностных компетенций, а также развитию творческих компетенций.

По своему содержанию лабораторные работы представляют собой наблюдения, измерения и опыты, тесно связанные с темой занятия. В пособие включены следующие виды заданий: 1) наблюдение и изучение физических явлений, 2) наблюдение и изучение свойств веществ, 3) измерение физических величин, 4) исследование зависимостей физическими величинами, 5) изучение физических законов.

Лабораторные работы составлены по разделам курса общей физики согласно разработанной автором рабочей программе.

Выполнение всех работ является обязательным для всех обучающихся. Лабораторные работы являются эффективным средством активизации и мотивации обучения физике, способствуют применению различных методов и приемов обучения для формирования у обучающихся системы прочных знаний, интеллектуальных и практических умений и навыков, помогают развитию мышления обучающихся, так как побуждают к выполнению умственных операций: анализу, синтезу, сравнению, обобщению и др.

Лабораторные работы составлены в виде инструкций. Каждая инструкция содержит цель работы, перечень оборудования, краткую теорию, ход выполнения работы (включая графы для составления отчета) и контрольные вопросы, обращающие внимание обучающихся на существенные стороны изучаемых явлений. Вопросы помогают глубже осмыслить производимые действия и полученные результаты и на их основе самостоятельно сделать необходимые выводы.

Основное назначение методических указаний – оказать помощь обучающимся в подготовке и выполнении лабораторных работ, а также облегчить работу преподавателя по организации и проведению лабораторных занятий.

Систематическое и аккуратное выполнение всей совокупности лабораторных работ позволит обучающемуся овладеть умениями самостоятельно ставить физические опыты, фиксировать свои наблюдения и измерения, анализировать их делать выводы в целях дальнейшего использования полученных знаний и умений.

Целями выполнения лабораторных работ является:

-    обобщение, систематизация, углубление, закрепление полученных теоретических знаний по конкретным темам дисциплины;

-    формирование умений применять полученные знания на практике, реализация единства интеллектуальной и практической деятельности;

-    развитие интеллектуальных умений у будущих специалистов; аналитических, проектировочных, конструктивных и др.

-    выработку при решении поставленных задач таких профессионально значимых качеств, как самостоятельность, ответственность, точность, творческая инициатива.

Для более эффективного выполнения лабораторных работ необходимо повторить соответствующий теоретический материал, а на занятиях, прежде всего, внимательно ознакомиться с содержанием работы и оборудованием.

В ходе работы необходимо строго соблюдать правила по технике безопасности; все измерения производить с максимальной тщательностью; для вычислений использовать микрокалькулятор.

После окончания работы каждый обучающийся должен предоставить отчет. Небрежное оформление отчета, исправление уже написанного недопустимо.

 

Лабораторная работа № 1

Сохранение механической энергии при движении тела под действием сил тяжести и упругости

Цель: 1) научиться измерять потенциальную энергию поднятого над землей тела и упруго деформированной пружины;

            2) сравнить две величины—уменьшение потенциальной энергии прикрепленного к пружине тела при его падении и увеличение потенциальной энергии растянутой пружины.

Приборы и материалы: 1) динамометр, жесткость пружины которого равна 40 Н/м; 2) линейка измерительная; 3) груз из набора по механике; масса груза равна (0,100 ±0,002) кг; 4) фиксатор; 5) штатив с муфтой и лапкой.

Основные сведения.

Если тело способно совершить работу, то говорят, что оно обладает энергией.

Механическая энергия тела – это скалярная величина, равная максимальной работе, которая может быть совершена в данных условиях.

Обозначается Е Единица энергии в СИ [1Дж = 1Н*м]

Кинетическая энергия – это энергия тела, обусловленная его движением.

Физическая величина, равная половине произведения массы тела на квадрат его скорости, называется кинетической энергией тела:

Кинетическая энергия – это энергия движения. Кинетическая энергия тела массой m, движущегося со скоростью  равна работе, которую должна совершить сила, приложенная к покоящемуся телу, чтобы сообщить ему эту скорость:

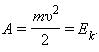
Наряду с кинетической энергией или энергией движения в физике важную роль играет понятие потенциальной энергии или энергии взаимодействия тел.

Потенциальная энергия – энергия тела, обусловленная взаимным расположением взаимодействующих между собой тел или частей одного тела. 

Потенциальная энергия тела в поле силы тяжести (потенциальная энергия тела, поднятого над землёй).

E_p = mgh

Она равна работе, которую совершает сила тяжести при опускании тела на нулевой уровень.

Растянутая (или сжатая) пружина способна привести в движение прикрепленное к ней тело, то есть сообщить этому телу кинетическую энергию. Следовательно, такая пружина обладает запасом энергии. Потенциальной энергией пружины (или любого упруго деформированного тела) называют величину

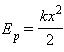, где k – жесткость пружины, х - абсолютное удлинение тела.

Потенциальная энергия упруго деформированного тела равна работе силы упругости при переходе из данного состояния в состояние с нулевой деформацией.

Потенциальная энергия при упругой деформации – это энергия взаимодействия отдельных частей тела между собой силами упругости.

Если тела, составляющие замкнутую механическую систему, взаимодействуют между собой только силами тяготения и упругости, то работа этих сил равна изменению потенциальной энергии тел, взятому с противоположным знаком:

A = –(E_p2 – E_p1).

По теореме о кинетической энергии эта работа равна изменению кинетической энергии тел:

A = E_k2 – E_k1

Следовательно   E_k2 – E_k1 = –(E_p2 – E_p1)      или        E_k1 + E_p1 = E_k2 + E_p2.

Сумма кинетической и потенциальной энергии тел, составляющих замкнутую систему и взаимодействующих между собой силами тяготения и силами упругости, остается неизменной.

Это утверждение выражает закон сохранения энергии в механических процессах. Он является следствием законов Ньютона.

Сумму E = E_k + E_p называют полной механической энергией.

Полная механическая энергия замкнутой системы тел, взаимодействующих между собой только консервативными силами, при любых движениях этих тел не изменяется. Происходят лишь взаимные превращения потенциальной энергии тел в их кинетическую энергию, и наоборот, или переход энергии от одного тела к другому.

Е = Е_к + Е_p = const 

Закон сохранения механической энергии выполняется только тогда, когда тела в замкнутой системе взаимодействуют между собой консервативными силами, то есть силами, для которых можно ввести понятие потенциальной энергии.

В реальных условиях практически всегда на движущиеся тела наряду с силами тяготения, силами упругости и другими консервативными силами действуют силы трения или силы сопротивления среды.

Сила трения не является консервативной. Работа силы трения зависит от длины пути.

Если между телами, составляющими замкнутую систему, действуют силы трения, то механическая энергия не сохраняется. Часть механической энергии превращается во внутреннюю энергию тел (нагревание).

Описание установки

Для работы используется установка, показанная на рисунке. Она представляет собой укрепленный на штативе динамометр с фиксатором 1.

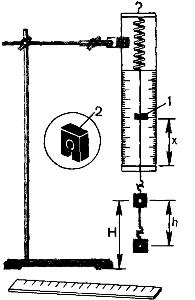
Пружина динамометра заканчивается проволочным стержнем с крючком. Фиксатор (в увеличенном масштабе он показан отдельно — помечен цифрой 2) — это легкая пластинка из пробки (размерами 5 Х 7 X 1,5 мм), прорезанная ножом до ее центра. Ее насаживают на проволочный стержень динамометра. Фиксатор должен перемещаться вдоль стержня с небольшим трением, но трение все же должно быть достаточным, чтобы фиксатор сам по себе не падал вниз. В этом нужно убедиться перед началом работы. Для этого фиксатор устанавливают у нижнего края шкалы на ограничительной скобе. Затем растягивают и отпускают.

Фиксатор вместе с проволочным стержнем должен подняться вверх, отмечая этим максимальное удлинение пружины, равное расстоянию от упора до фиксатора.

Если поднять груз, висящий на крючке динамометра, так, чтобы пружина не была растянута, то потенциальная энергия груза по отношению, например, к поверхности стола равна mgh. При падении груза (опускание на расстояние x = h) потенциальная энергия груза уменьшится на

Е₁=mgh

а энергия пружины при ее деформации увеличивается на

Е₂=kx²/2

Порядок выполнения работы

1. Груз из набора по механике прочно укрепите на крючке динамометра.

2. Поднимите рукой груз, разгружая пружину, и установите фиксатор внизу у скобы.

3. Отпустите груз. Падая, груз растянет пружину. Снимите груз и по положению фиксатора измерьте линейкой максимальное удлинение х пружины.

4. Повторите опыт пять раз. Найдите среднее значение h и х

5. Подсчитайте Е_1ср=mgh и  Е_2ср=kx²/2

6. Результаты занесите в таблицу

7. Сравните отношение Е_1ср/ Е_2ср с единицей и сделайте вывод о погрешности, с которой был проверен закон сохранения энергии.

8. Ответьте на контрольные вопросы.

Контрольные вопросы

1.Раскройте понятие механической энергии?

2.Какая энергия называется кинетической? По какой формуле она находится?

3.Какая энергия называется потенциальной? По какой формуле она находится?

4. Что называется полной механической энергией?

5.Сформулируйте закон сохранения механической энергии.

6. Как связано изменение потенциальной энергии падающего груза с изменением энергии
пружины, растянутой при его падении?

 

Вариант выполнения измерений:

1. Определяем максимальное удлинение х пружины и заносим в таблицу:

№ опыта	h=хmax, м	hср=хср, м	Е1ср, Дж	Е2ср, Дж	Е1ср/ Е2ср
1	0,048
2	0,054
3	0,052
4	0,050
5	0,052

2. Выполняем расчеты по методичке.

 

Лабораторная работа № 2

Изучение особенностей силы трения (скольжения)

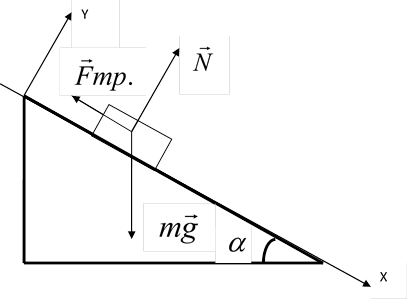
Цель работы: изучить зависимость силы трения от различных факторов и определить коэффициент трения скольжения.

Оборудование: динамометр, грузы с двумя крючками- 2 шт., лист бумаги, лист наждачной бумаги штатив, направляющая рейка, каретка, секундомер с двумя датчиками.

Краткая теория

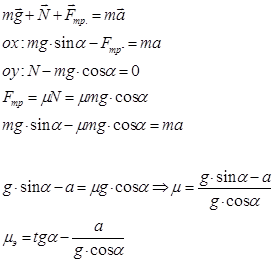(1).

 

 

 

 

 

 

 

 

 

 

Ход работы:

I.                   Изучение зависимости силы трения скольжения от рода трущихся поверхностей от силы давления и независимости от площади трущихся поверхностей.

 

Измерение силы трения скольжения

1.Измерьте силу трения скольжения бруска с двумя грузами: а) по поверхности линейки; б) по гладкой бумаге; в) по наждачной бумаге.

2. Результаты измерений запишите в таблицу:

Виды трущихся поверхностей	Сила трения скольжения, H
Дерево по дереву
Дерево по гладкой бумаге
Дерево по наждачной бумаге

3. Сделайте вывод как сила трения: а) зависит от рода трущихся поверхностей, б) зависит от шероховатости трущихся поверхностей?

4. Положите на линейку брусок большой гранью, а на него – груз и измерьте силу трения скольжения по линейке F_тр.ск= ________.

5. Положите на брусок второй груз и снова измерьте силу трения скольжения бруска по линейке F_тр.ск= ________.

6. Положите на линейку брусок меньшей гранью, поставьте на него два груза и снова измерьте силу трения скольжения бруска по линейке F_тр.ск= ________.

7.Сделайте вывод, зависит ли сила трения скольжения: а) от силы давления (и если зависит, то как), б) от площади трущихся поверхностей при постоянной силе давления?

II. Определение коэффициента трения скольжения.

1.      Установить направляющую рейку при помощи штатива под углом 30⁰, к секундомеру подключить датчики, отпустить каретку и определить время движения каретки между датчиками.

2.      Вычислить коэффициент трения, пользуясь формулой (1):

, s=____, t=_____, a=_____, =______.

Контрольные вопросы

1.      Какие виды сил трения вы знаете?

2.      От чего зависит коэффициент трения?

3.      Какими способами можно увеличить или уменьшить силу трения скольжения?

4.      Каково значение явления трения в природе и технике?

 

 

Лабораторная работа № 3

Исследование движения тела под действием постоянной силы

Цель работы: 1. выяснить, зависит ли сила трения скольжения от силы нормального давления, если зависит, то как.

                           2. Определить коэффициент трения дерева по дереву.

   Приборы и материалы: динамометр, деревянный брусок, деревянная линейка или деревянная плоскость, набор грузов по 100 г.

Теория

   Сила трения – это сила, которая возникает в том месте, где тела соприкасаются друг с другом, и препятствует перемещению тел.

   Сила трения — это сила электромагнитной природы.

   Возникновение силы трения объясняется двумя причинами:

   1) Шероховатостью поверхностей
   2) Проявлением сил молекулярного взаимодействия.

   Силы трения всегда направлены по касательной к соприкасающимся поверхностям и подразделяются на силы трения покоя, скольжения, качения.

   В данной работе исследуется зависимость силы трения скольжения от веса тела.

   Сила трения скольжения – это сила, которая возникает при скольжении предмета по какой-либо поверхности. По модулю она почти равна максимальной силе трения покоя. Направление силы трения скольжения противоположно направлению движения тела. Сила трения в широких пределах не зависит от площади соприкасающихся поверхностей. В данной работе надо будет убедиться в том, что сила трения скольжения пропорциональна силе давления (силе реакции опоры): 
   Fтр=μN, где μ - коэффициент пропорциональности, называется коэффициентом трения. Он характеризует не тело, а сразу два тела, трущихся друг о друга.        

 Ход работы

1. Определите цену деления шкалы динамометра.

2. Определите массу бруска. Подвесьте брусок к динамометру, показания динамометра — это вес бруска. Для нахождения массы бруска разделите вес на g. Принять g=10 м/с².

2. Положите брусок на горизонтально расположенную деревянную линейку. На брусок поставьте груз 100 г.

3. Прикрепив к бруску динамометр, как можно более равномерно тяните его вдоль линейки. Запишите показания динамометра, это и есть величина силы трения скольжения.

4. Добавьте второй, третий, четвертый грузы, каждый раз измеряя силу трения. С увеличением числа грузов растет сила нормального давления.

5. Результаты измерений занесите в таблицу.

№ опыта	Масса бруска,  m1 , кг	Масса груза, m2 , кг	Общий вес тела (сила нормального давления), Р=N=(m1+m2)g, Н	Сила трения, Fтр, Н	Коэффициент трения, μ	Среднее значение коэффициента трения, μср
1
2
3
4
5

6.Сделайте вывод: зависит ли сила трения скольжения от силы нормального давления, и если зависит, то как?

7. В каждом опыте рассчитать коэффициент трения по формуле: . Принять g=10 м/с².

    Результаты расчётов занести в таблицу.

8. По результатам измерений постройте график зависимости силы трения от силы нормального давления. При построении графика по результатам опытов экспериментальные точки могут не оказаться на прямой, которая соответствует формуле. Это связано с погрешностями измерения. В этом случае график надо проводить так, чтобы примерно одинаковое число точек оказалось по разные стороны от прямой. После построения графика возьмите точку на прямой (в средней части графика), определите по нему соответствующие этой точке значения силы трения и силы нормального давления и вычислите коэффициент трения . Это и будет средним значением коэффициента трения. Запишите его в таблицу.

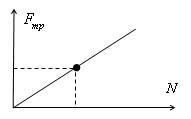
9. Исходя из цели работы, запишите вывод и ответьте на контрольные вопросы.

Контрольные вопросы

1. Что называется силой трения?

2. Какова природа сил трения?

3. Назовите основные причины, от которых зависит сила трения?

4. Перечислите виды трения.

5. Можно ли считать явление трения вредным? Почему?

   Вариант выполнения лабораторной работы:

5. Результаты измерений:

№ опыта	Масса бруска, m1 , кг	Масса груза, m2 , кг	Общий вес тела  (сила нормального давления), Р=N=(m1+m2)g, Н	Сила трения, Fтр, Н	Коэффициент трения, μ	Среднее значение коэффициента трения, μср
1	0,07	0,1		0,4
2		0,2		0,6
3		0,3		0,8
4		0,4		1
5		0,5		1,2

 

Лабораторная работа № 4

Изучение закона сохранения импульса

Цель: экспериментально проверить справедливость закона сохранения импульса тел при прямом упругом соударении

Оборудование: 1. Два металлических шарика разной массы, рама для подвеса шариков, измерительная линейка.

Теория

   Величина, равная произведению массы материальной точки на ее скорость, называется импульсом.

p=mυ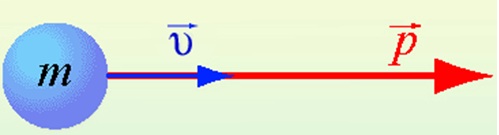  

p — импульс тела

m — масса тела

υ — скорость тела   

   Импульс тела направлен в ту же сторону, что и скорость тела.

   Единицей измерения импульса в СИ является 1 кг·м/с.

   Изменение импульса тела происходит при взаимодействии тел, например, при ударах.

   Для системы материальных точек полный импульс равен сумме импульсов. При этом следует иметь в виду, что импульс – это векторная величина, и поэтому в общем случае импульсы складываются как векторы, т.е. по правилу параллелограмма.

   Если на систему тел не действуют внешние силы со стороны других тел, такая система называется замкнутой. Замкнутая система – это система тел, которые взаимодействуют только друг с другом.

   Закон сохранения импульса: в замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой.

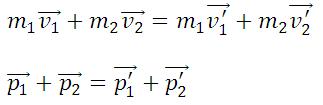
m₁, m₂ — массы взаимодействующих тел, кг

υ₁, υ₂ — скорости тел до столкновения, м/с

υ'₁, υ'₂ — скорости тел после столкновения, м/с

   Закон сохранения импульса можно сформулировать и так: если на тела системы действуют только силы взаимодействия между ними («внутренние силы»), то полный импульс системы тел не изменяется со временем, т.е. сохраняется. Этот закон применим к системе, состоящей из любого числа тел. Отметим еще раз, что импульс – величина векторная, поэтому сохранение полного импульса означает сохранение не только его величины, но и направления.

   Закон сохранения импульса выполняется при распаде тела на части и при абсолютно неупругом ударе, когда соударяющиеся тела соединяются в одно. Если распад или удар происходят в течение малого промежутка времени, то закон сохранения импульса приближенно выполняется для этих процессов даже при наличии внешних сил, действующих на тела системы со стороны тел, не входящих в нее, т.к. за малое время внешние силы не успевают значительно изменить импульс системы.

   Под ударом в механике понимается кратковременное взаимодейс­твие двух или более тел, возникающее в результате их соприкосно­вения (соударение шаров, удар молота о наковальню и др.). Самым простым является прямой (центральный) удар, то есть такой удар, при котором скорости соударяющихся тел до удара направлены по линии, соединя­ющей центры тел. При соударении взаимодействие длится такой короткий промежуток времени (иногда измеряемый тысячными долями секунды) и возни­кают столь большие внутренние силы взаимодействия, что внешними силами можно пренебречь и систему соударяющихся тел можно считать замкнутой и применять к ней закон сохранения импульса.

   В зависимости от упругих свойств тел соударения могут проте­кать весьма различно. Принято выделять два крайних случая: абсо­лютно упругий и абсолютно неупругий удары.

   Абсолютно упругим называется удар, при котором после взаимодействия тела полностью восстанавливают свою форму. Таких ударов в природе не существует, так как всегда часть энергии затрачивается на необратимую деформацию тел. Однако для некоторых тел, например стальных закаленных шаров, потерями механической энергии при столкновении можно пренебречь и считать удар абсолютно упру­гим. В случае центрального абсолютно упругого удара двух тел с массами m₁, m₂ и скоростями υ₁, υ₂ до удара и υ′₁, υ′₂ после удара можно записать закон сохранения импульса тел:

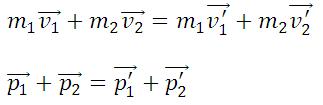
   Абсолютно неупругим называется удар, при котором после соп­рикосновения тел они не восстанавливают полностью свою форму, со­единяются вместе и движутся как единое целое с одной скоростью. При этом ударе часть их механической энергии переходит в работу деформации тел (внутреннюю энергию). Столкновение двух шаров из пластилина, когда после столкновения шары слипаются и движутся вместе, является примером абсолютно неупругого удара. В случае центрального абсолютно неупругого удара двух тел с массами m₁, m₂  движущихся со скоростями υ₁, υ₂  до удара и υ′ после удара можно записать законы сохранения импульса тел:

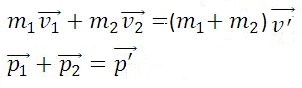
   Закон сохранения импульса служит основой для объяснения обширного круга явлений природы, применяется в различных науках:

1.      Закон строго выполняется в явлениях отдачи при выстреле, явлении реактивного движения, взрывных явлениях и явлениях столкновения тел.

2.      Закон сохранения импульса применяют: при расчетах скоростей тел при взрывах и соударениях; при расчетах реактивных аппаратов; в военной промышленности при проектировании оружия; в технике - при забивании свай, ковке металлов и т.д

Описание работы

Установка состоит из двух стальных шаров, на длинных подвесах и измерительной линейки под шарами. Центры масс соприкасающихся шаров лежат на одном уровне от точки подвеса. Отведя один из шаров (например, большей массы) в сторону и отпустив его, можно произвести прямой (центральный) удар шаров.

Если до столкновения один из шаров покоился υ₂=0, то выражение закона сохранения импульса упростится. При прямом ударе оба шара после столкновения движутся по одной прямой, поэтому от векторной формы записи закона сохранения импульса можно перейти к алгебраической и учитывая, что после столкновения оба шара движутся в одном направлении, получим:

m₁∙υ₁= m₁∙υ′₁ + m₂∙υ′₂ 

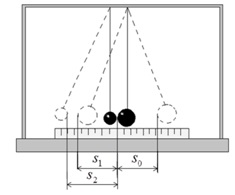
   рис. 2

   Для определения скорости первого шара υ₁ до удара  и скоростей шаров υ′₁ и υ′₂ после удара воспользуемся законом сохранения механической энергии. Потенциальная энергия шара в положении максимального отклонения равняется его кинетической энергии при ударе , отсюда .

   Высоту подъёма шара можно определить по его максимальному отклонению s от положения равновесия (рис.3а).

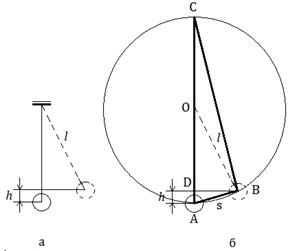
рис. 3

Треугольник АВС прямоугольный (опирается на диаметр). Катет АВ является средней пропорциональной величиной между гипотенузой АС=2l и своей проекцией на гипотенузу АD (рис.3б):  АВ²=АС·AD то есть , откуда . Следовательно, величины скоростей можно выразить так: 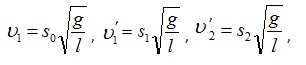где S₀, S₁ - максимальные отклонения первого шара до и после удара; S₂ - максимальное отклонение второго шара после удара.

Запишем уравнение закона сохранения через выражения скоростей:

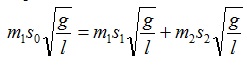  или m₁∙S₀= m₁∙S₁ + m₂∙S₂.

Таким образом, проверка закона сохранения импульса в данной работе сводится к проверке справедливости последнего уравнения.

 При малых углах отклонения шара от положения равновесия S₀, S₁ и S₂ можно заменить соответствующими величинами, отсчитанными по горизонтальной шкале.

Выполнение работы

1. Перенесите рисунок 2 в отчет по работе.

2. Подготовьте в тетради таблицу для записи результатов измерений и вычислений:

№	m1, г	m2, г	S0, мм	S1, мм	S2, мм	m1∙S0, г∙мм с	m1∙S1, г∙мм с	m2∙S2, г∙мм с	m1∙S1 + m2∙S2, г∙мм с
1
2
3

3. Определите массы шаров m₁ и m₂. Запишите их результат в таблицу.

4. Отрегулируйте подвеску шаров так, чтобы их центры и точка касания находились на одной горизонтальной линии.

5. Отклоните шар большей массы на 3 см от положения равновесия (S₀) и затем отпустите его. Заметьте максимальное отклонение шара большей массы после удара (S₁). Повторите опыт 5 раз и найдите среднее значение отклонения S_1ср. Запишите его в таблицу (S₁).

6. Повторите опыт, но теперь заметьте после удара максимальное отклонение шара с меньшей массой (S₂). Повторите опыт 5 раз, и найдите среднее значение отклонения S_2ср. Запишите его в таблицу (S₂).

7. Повторите опыт, отклоняя шар большей массы на 4 см и 5 см. Результаты измерений запишите в таблицу.

8. Используя значения S₀, S₁ и S₂, вычислите импульс шара до удара m₁∙S₀ и сумму импульсов шаров после удара m₁∙S₁ + m₂∙S₂ и внесите в таблицу их результаты.

9. Сравните импульс шара до удара с суммой импульсов шаров после удара. Запишите вывод по полученным результатам работы.

10. Ответьте на контрольные вопросы.

Контрольные вопросы

1. Что называется импульсом материальной точки? По какой формуле он находится? В каких единицах он измеряется?

2. Импульс – величина векторная или скалярная?

3. Запишите формулу и формулировку закона сохранения импульса.

4. При каких условиях выполняется закон сохранения импульса?

5. Какое соударение называется абсолютно упругим?

6. Для каких видов соударений выполняется закон сохранения импульса?

Вариант выполнения измерений

1. Определяем массы шариков m₁ и m₂ при помощи динамометра (или весов) и записываем в таблицу:

m₁=62 г

m₂=27,5 г

2. Отклоняем большой шар от положения равновесия на 3 см и отпускаем его. 

S₀=3 см=30 мм

Замечаем его максимальное отклонение после удара. Повторяем опыт 5 раз, находим среднее значение отклонения и записываем в таблицу S_1ср.

S₁=13мм   S₁=15мм   S₁=18мм    S₁=14мм   S₁=16мм

S_1ср=(13мм+15мм+18мм+14мм+16мм)/5=15,2 мм

3. Повторяем этот же опыт, но теперь замечаем после удара отклонение шара меньшей массы. Повторяем опыт 5 раз, находим среднее значение и записываем в таблицу S_2ср.

S₂=31мм   S₂=34мм   S₂=36мм    S₂=35мм   S₂=32мм

S_2ср=(31мм+34мм+36мм+35мм+32мм)/5=34мм

4. Повторяем опыт, отклоняя шар большей массы на 4 см и 5 см. 

S₀=4 см=40 мм

S₁=18 мм   S₁=19 мм   S₁=23 мм    S₁=22 мм   S₁=18 мм

S_1ср= (18 мм+19 мм+23 мм+22 мм+18 мм)/5=20 мм

S₂=43 мм   S₂=44 мм   S₂=46 мм    S₂=47 мм   S₂=45 мм

S_2ср= (43 мм + 44 мм + 46 мм + 47 мм + 45 мм)/5=45 мм

S₀=5 см=50 мм

Результаты измерений записываем в таблицу.

№	m1, г	m2, г	S0, мм	S1, мм	S2, мм	m1∙S0, г∙мм с	m1∙S1, г∙мм с	m2∙S2, г∙мм с	m1∙S1 + m2∙S2, г∙мм с
1	62,0	27,5	30	15	34
2	62,0	27,5	40	20	45
3	62,0	27,5	50	25	56

 

 

Лабораторная работа № 5

Сравнение работы силы с изменением кинетической энергии тела

Цель: сравнить изменение кинетической энергии тела при соскальзывании с наклонной плоскости с работой равнодействующей сил. Сделать вывод о выполнении теоремы о кинетической энергии.

Оборудование: штатив, широкая деревянная линейка, деревянный брусок, линейка, секундомер.

Ход работы

1)      Установите с помощью штатива широкую линейку наклонно, так чтобы брусок соскальзывал по наклонной плоскости.

Измерьте линейкой длину l и высоту h наклонной плоскости.

2)      Cпустите брусок сверху плоскости. Измерьте с помощью секундомера время соскальзывания t.

3)      Скорость тела в конце траектории: , т.к. начальная скорость равна нулю. Чтобы найти ускорение тела, используйте формулу перемещения при равноускоренном движении: .

4)      Изменение кинетической энергии тела: , где m – масса тела.

5)      Работа равнодействующей сил равна: коэффициент трения дерева по дереву.

6)      Рассчитайте: , результаты округляйте до четырёх знаков после запятой.

7)      Приравняйте работу равнодействующей сил и изменение кинетической энергии тела: .

8)      Массу тела и длину наклонной плоскости можно сократить:. Рассчитайте значения в левой и правой частях равенства, результаты округляйте до десятых.

9)      Результаты занесите таблицу:

Высота наклонной плоскости h, м	Длина наклонной плоскости l, м	Время соскальзывания тела t, с	, м/с2	, м/с2

Контрольные вопросы:

1. Как найти кинетическую энергию тела?

2. Сформулируйте закон сохранения кинетической энергии.

Лабораторная работа № 6

Изучение зависимости периода колебаний нитяного маятника от длины нити

Цель работы: установить математическую зависимость периода нитяного маятника от длины нити маятника.

Оборудование: электронный секундомер, измерительная лента, шарик с отверстием, нить, штатив с муфтой и кольцом.

Краткая теория

Математическим маятником называется материальная точка, подвешенная на невесомой и нерастяжимой нити. Моделью может служить тяжёлый шарик, размеры которого весьма малы по сравнению с длинной нити, на которой он подвешен (не сравнимы с расстоянием от центра тяжести до точки подвеса).

Учёные Галилей, Ньютон, Бессель и др. установили следующие законы колебания математического маятника:

1.Период колебания математического маятника не зависит от массы маятника и от амплитуды, если угол размаха не превышает 10^о.

2.Период колебания математического маятника прямо пропорционален квадратному корню из длины маятника и обратно пропорционален квадратному корню из ускорения свободного падения. На основании этих законов можно написать формулу для периода колебаний математического маятника:

.

Используя модель и законы колебаний математического маятника, можно пронаблюдать свободные колебания, а также с их помощью определить ускорение свободного падения для своей местности и сравнить со справочным значением g.

Ускорение свободного падения может быть вычислено по формуле

.

Ход работы

1.      Укрепить нить маятника в держателе штатива.

2.      Измерить длину маятника (длина маятника считается от точки подвеса до центра тяжести шарика).

3.      Отклонить шарик на угол не более 10° и отпустить.

4.      Определить время, за которое маятник совершил 20 колебаний.

5.      Вычислить период колебания маятника, используя формулу .

6.      Повторить опыт еще три раза, уменьшая (или увеличивая) длину нити маятника.

 

7.      Результаты занести в таблицу.

8.      Сделать вывод о зависимости периода нитяного маятника от длины его нити.

Контрольные вопросы:

1.Что называют периодом колебаний маятника?

2.Что называют частотой колебаний маятника? Какова единица частоты колебаний?

3.От каких величин и как зависит период колебаний математического маятника?

4.От каких величин и как зависит период колебаний пружинного маятника?

5.Изобразите математический маятник в крайней правой точке и покажите на чертеже силы, действующие на шарик в данной точке траектории. Нарисуйте равнодействующую сил. Как меняется величина и направление равнодействующей сил в течение периода?

Лабораторная работа №7

Измерение влажности воздуха

Цель: освоить прием определения относительной влажности воздуха, основанный на использовании психрометра.

Оборудование: 1. Психрометр.

Выполнение работы

Задание 1. Измерить влажность воздуха с помощью психрометра.

Подготовили таблицу для записи результатов измерений и вычислений:

№ опыта	tсухого, 0С	tвлажного, 0С	Δt, 0С	φ, %
1	24	21	3	77

Рассмотрели устройство психрометра.

Показания сухого термометра t_сухого =24⁰С.

Показания влажного термометра t_{влажного} =21⁰С.

Разность показаний термометров:

Δt = t_сухого - t_{влажного}

Δt = 24⁰С - 21⁰С=3⁰С

По психрометрической таблице определяем влажность воздуха φ:

Психрометрическая таблица.

tсухого,0С	Разность показаний сухого и влажного термометров
	0	1	2	3	4	5	6	7	8	9	10	11
21	100	91	83	75	67	60	52	46	39	32	26	20
22	100	92	83	76	68	61	54	47	40	34	28	22
23	100	92	84	76	69	61	55	48	42	36	30	24
24	100	92	84	77	69	62	56	49	43	37	31	26
25	100	92	84	77	70	63	57	50	44	38	33	27
26	100	92	85	78	71	64	58	51	45	40	34	29

φ=77%

Вывод: в ходе лабораторной работы определили относительную влажность воздуха в кабинете, она равна 77%. Это повышенная влажность воздуха.

Контрольные вопросы

1.Какой пар называется насыщенным? Что такое динамическое равновесие, точка росы, парциальное давление?

2.Почему показания смоченного термометра меньше, чем сухого?

3.Как, зная точку росы, можно определить парциальное давление?

4.Сухой и влажный термометры психрометра показывают одинаковую температуру. Какова относительная влажность воздуха?

 

Лабораторная работа №8

Измерение поверхностного жидкости

Цель: определить коэффициент поверхностного натяжения воды методом отрыва капель.

   Оборудование: сосуд с водой, шприц, сосуд для сбора капель.

Краткая теория

На каплю, висящую на конце узкой трубочки, действуют две силы: сила тяжести , направленная вертикально вниз, и сила поверхностного натяжения жидкости , распределенная вдоль границы жидкости с краем трубки и направленная по касательной к поверхности жидкости перпендикулярно этой границе. Сила поверхностного натяжения, действующая на небольшой участок границы длиной , равна , где σ – коэффициент поверхностного натяжения жидкости. Условие равновесия капли на конце трубочки состоит в том, что векторная сумма сил, действующих на отдельные элементы границы, равна по модулю и противоположна по направлению силе тяжести. Величина  по мере увеличения массы капли остается неизменной, но в равновесии капля принимает такую форму, что угол наклона силы поверхностного натяжения к вертикали α удовлетворяет условию , где  – длина границы жидкости с трубочкой. С увеличением массы капли угол α уменьшается и, наконец, достигает нуля, а cosα = 1. При дальнейшем увеличении массы условие равновесия капли уже не может быть выполнено, и капля отрывается. Отсюда, принимая, что , где d – внутренний диаметр трубочки, получаем:  или  (1).

Ход работы

1.Измерить внутренний диаметр d наконечника шприца. Для измерения можно воспользоваться остро отточенным карандашом. Вдвинув карандаш в наконечник до упора, пометьте границу соприкосновения наконечника с карандашом. Диаметр карандаша на уровне этой границы можно принять за внутренний диаметр наконечника и измерить его с помощью штангенциркуля или микрометра.

2.Набрать в шприц 4–5 мл воды и, держа его вертикально и плавно нажимая на поршень, вылить 3–4 мл в стаканчик, считая капли. Измерение количества капель N провести не менее трех раз, затем по общей массе вытекшей воды общ m (пользуйтесь шкалой на шприце!) найти среднюю массу капли m и погрешность ее определения Δm. Результаты занести в таблицу

 

 

Выполнение работы

1.      Начертили таблицу:

№ опыта	Масса капель m, кг	Число капель n	Диаметр канала шприца d, м	Поверхност-ное натяжение σ, Н/м	Среднее значение поверхностного натяжения σср, Н/м	Табличное значение поверхност-ного натяжения σтаб, Н/м	Относительная погрешность δ %
1	1*10-3	21	2,5*10-3	0,066	0,069	0,072	41,67
2	2*10-3	40	2,5*10-3	0,069
3	3*10-3	59	2,5*10-3	0,071

Вычисляем поверхностное натяжение по формуле 

 

Находим среднее значение поверхностного натяжения по формуле:  

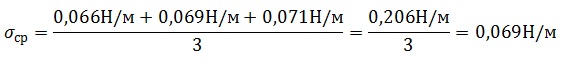
Определяем относительную погрешность методом оценки результатов измерений.

 

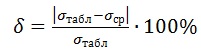
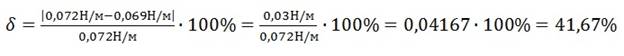
Вывод:

Контрольные вопросы

1. Коэффициент поверхностного натяжения керосина 0,024 н/м. Больше или меньше масса капли керосина по сравнению с каплей воды, если капать из одной и той же пипетки?

2. Объясните подробно, почему маленькие капельки жидкости могут долго висеть не отрываясь.

3. Почему, прежде чем покрыть штукатурку масляной краской, предварительно производят грунтовку олифой?

4. Приведите свои примеры действия силы поверхностного натяжения.

 

Лабораторная работа №9

Наблюдение кристаллизации. Изучение деформации растяжения

Цель работы: научиться создавать кристаллы, пронаблюдать рост кристалла. Определить модуль упругости резины при растяжении.

Оборудование: поваренная соль, дистиллированная вода, воронка, деревянная шпажка, марля, стаканы, нитка (леска), резиновый шнур длиной 25—30 см и сечением 4— 10 мм², набор грузов по 0,1 кг, штатив, линейка, штангенциркуль или микрометр.

Краткая теория

Существуют два простых способа выращивания кристаллов из раствора: охлаждение насыщенного раствора соли и его выпаривание. Первым этапом при любом из двух способов является приготовление насыщенного раствора. С появлением центров кристаллизации избыток вещества выделяется из раствора. Избыток вещества из раствора выпадает в виде кристаллов; количество кристаллов тем больше, чем больше центров кристаллизации в растворе. Центрами кристаллизации могут служить загрязнения на стенках посуды с раствором, пылинки, мелкие кристаллики. Чтобы вырастить крупный кристалл, в тщательно отфильтрованный насыщенный раствор нужно внести кристаллик - затравку, заранее прикрепленный на волосе или тонкой леске, предварительно обработанной спиртом.

Можно вырастить кристалл без затравки. Для этого волос или леску обрабатывают спиртом и опускают в раствор так, чтобы конец висел свободно. На конце волоса или лески может начаться рост кристалла.

Если стакан с раствором прикрыть так, чтобы вода из раствора могла испаряться, то вскоре раствор станет пересыщенным и начнется рост кристалла. Во время роста кристалла стакан с раствором лучше всего держать в теплом сухом месте, где температура в течение суток остается постоянной. На выращивание крупного кристалла в зависимости от условий эксперимента может потребоваться от нескольких дней до нескольких недель.

При установившейся упругой деформации равнодействующая всех внутренних сил упругости, возникающих в теле в любом его сечении, уравновешивает внешние силы, действующие на тело.

Согласно закону Гука, напряжение  и вызванное им относительное удлинение  пропорциональны: =Е, где Е— модуль упругости.

После преобразования этого выражения получим:

 или .

Для экспериментального определения модуля упругости нужно измерить все величины: деформирующую силу F (F=mg), сечение образца S (), его первоначальную длину l₀ и удлинение l.

 

 

 

 

Ход работы

I.       Наблюдение роста кристаллов из раствора.

1.Вымыть два стакана, простерилизовать их. 2.Взять 200 г дистиллированной воды, растворить в ней 50 г поваренной соли (10 чайных ложек). Профильтровав, перелить раствор в другой стакан. 3.На шпажку прикрепить нить, обработанную
спиртом, так, чтобы нить не доставала до дна стакана (см. рисунок).

4.Опустить нить в стакан с фильтрованным раствором.

5.Пронаблюдать рост кристаллов в стакане.

6.Сделать вывод.

__________________________________________________________________.

II.    Изучение деформации растяжения.

1. Измерить с помощью штангенциркуля или микрометра толщину шнура и вычислить площадь его поперечного сечения S.

3. Подвешивая к шнуру грузы массой 0,1 кг, 0,2 кг, 0,3 кг, измерить соответствующие абсолютные удлинения шнура: и вычислить относительные удлинения шнура.

4. По результатам измерений вычислить модуль упругости резины Е и оценить погрешности эксперимента:

- относительная погрешность,

 - абсолютная погрешность.

5. Результаты измерений и вычислений занести в таблицу:

измерено						вычислено
№ п/п	m, кг	d, м	S, м2	l0, м	l, м	l, м	F, Н	E, Па	Eср, Па	E, Па	, %
1
2
3

6. Сделать вывод

Контрольные вопросы

1. При каких условиях возникают кристаллы в жидких растворах?

2. Как влияют скорости роста граней на форму кристалла?

3. Каков простейший метод выращивания кристаллов?

4.Какие виды деформаций вы знаете?

5. Изменяется ли внутренняя энергия деформированных тел?

 

 

 

 

Лабораторная работа №10

Изучение теплового расширения твердых тел

Цель работы: научиться определять коэффициент линейного расширения твёрдого тела по экспериментальным данным.

Краткая теория. Тепловое расширение представляет собой изменение размеров тел при их нагревании. Количественно тепловое расширение характеризуется коэффициентами линейного и объемного расширения.

Пусть тело при температуре T₁ имеет длину ℓ₁, а при температуре (где- сравнительно небольшой интервал температур) имеет длину ℓ₂, тогда коэффициент линейного расширения определяется из соотношения:

, (1)

т.е. физический смысл коэффициента линейного расширения α- коэффициент линейного расширения α показывает, на какую долю своего первоначального значения изменяются линейные размеры тела при изменении температуры на один Кельвин.

Аналогично коэффициент объемного расширения β определяется из соотношения:

, (2)

т.е. коэффициент объемного расширения β равен относительному изменению объемапри изменении температуры на 1 К, или показывает, на какую часть изменяется каждая единица начального объема при изменении температуры на 1 К.

Оборудование: набор лабораторный «Тепловые явления».

Ход работы

1. Для наблюдения за расширением твердых тел (проволоки) собрать установку

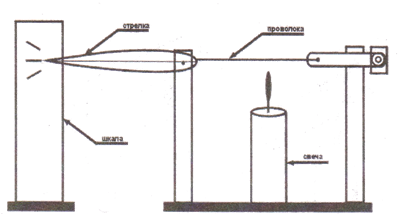
2. Под проволоку поместить свечу и наблюдать за изменением положения стрелки, убрать свечу и описать наблюдаемое явление

3. Выполнить работу для других видов проволоки.

4. Определить коэффициент линейного расширения твёрдого тела по экспериментальным данным

5. Результаты измерений и вычислений занести в таблицу:

вещество	l0, м	T0, К	T, К	l, м	, -1К	т, -1К	,%
медь
алюминий
сталь

6. По результатам измерений оценить погрешности эксперимента

:

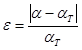7. Сделать вывод:

Контрольные вопросы

1.      Дайте определение коэффициента линейного теплового расширения твердого тела. В каких единицах он измеряется?

2.      Запишите, как зависит длина тела от его температуры?

3.      Как коэффициент линейного расширения связан с коэффициентом объемного расширения для изотропных твердых тел?

4.      Как с физической точки зрения объяснить увеличение размеров твердого тела при возрастании его температуры?

 

Лабораторная работа №11

Изучение особенностей теплового расширения воды

Цель работы: изучить свойства воды, связанные с тепловым расширением, теплопроводностью.

Оборудование: набор лабораторный «Тепловые явления».

 

Краткая теория

Жидкости расширяются значительно сильнее твердых тел. Они также расширяются во всех направлениях. Вследствие большой подвижности молекул жидкость принимает форму сосуда, в котором она находится, причем следует учитывать и тепловое расширение сосуда. Расширение жидкости в трубках также представляет собой объемное расширение.

Коэффициент объемного расширения слабо зависит от температуры. Вода является исключением и коэффициент расширения воды сильно зависит от температуры, а в интервале от 0 до 4 ⁰С принимает отрицательное значение. Другими словами, объём воды уменьшается от 0 до 4⁰С, а затем возрастает.

 

 

 

 

 

Ход работы

1. Наполнить пробирку водой и плотно закрыть пробкой с трубочкой. Начальный уровень отметить маркером. Пробирку нагреть при помощи свечи. 2. Когда уровень воды поднимется на 20-30 мм, нагревание прекратить и поместить пробирку в стакан с водой.
3. Описать наблюдаемое явление. Сделать вывод
4.Навлить в пробирку воды, заткнуть ее пробкой с отверстием. Взять за дно. Нагреть, как показано на рисунке 2, до кипения воды. 5. Сделать вывод

6. Наполнить большую пробирку холодной водой, измерить температуру и вылить воду в стакан. t₁₌__________.

7. Наполнить ту же пробирку горячей водой, измерить температуру, вылить и эту воду в стакан.t₂₌______________.

8. Измерить температуру получившейся смеси, t_э=________.

9. Составить уравнение теплового баланса и рассчитать температуру смеси t=____.

10. Сравнить t и t_э и сделать вывод

Контрольные вопросы

1.      Объясните особенности теплового расширения воды.

2.      Какое значение имеет тепловое расширение тел в природе и технике.

3.      Дайте определение удельной теплоемкости тела.

4.      В чем смысл теплового баланса?

 

Список использованной литературы

 

1. Дмитриева В. Ф. Физика для профессий и специальностей технического профиля: учебник для образовательных учреждений сред. проф. образования. — М., 2014.
2. Дмитриева В. Ф. Физика для профессий и специальностей технического профиля. Сборник задач: учеб. пособие для образовательных учреждений сред. проф. образования. — М., 2014.
3. Дмитриева В. Ф., Васильев Л. И. Физика для профессий и специальностей технического профиля. Контрольные материалы: учеб. пособия для учреждений сред. проф. образования / В. Ф. Дмитриева, Л. И. Васильев. — М., 2014.
4. Дмитриева В. Ф. Физика для профессий и специальностей технического профиля. Лабораторный практикум: учеб. пособия для учреждений сред. проф. образования / В. Ф. Дмитриева, А. В. Коржуев, О. В. Муртазина. — М., 2015.
5. Дмитриева В.Ф. Физика для профессий и специальностей технического профиля: электронный учеб.-метод. комплекс для образовательных учреждений сред. проф. образования. — М., 2014.
6. Дмитриева В. Ф. Физика для профессий и специальностей технического профиля: электронное учебное издание (интерактивное электронное приложение) для образовательных учреждений сред. проф. образования. — М., 2014.
7. Касьянов В. А. Иллюстрированный атлас по физике: 10 класс.— М., 2010.
8. Касьянов В. А. Иллюстрированный атлас по физике: 11 класс. — М., 2010.
9. Трофимова Т. И., Фирсов А. В. Физика для профессий и специальностей технического и естественно-научного профилей: Сборник задач. — М., 2013.
10. Трофимова Т. И., Фирсов А. В. Физика для профессий и специальностей технического и естественно-научного профилей: Решения задач. — М., 2015.
11. Трофимова Т. И., Фирсов А. В. Физика. Справочник. — М., 2010.
12. Фирсов А. В. Физика для профессий и специальностей технического и естественно-научного профилей: учебник для образовательных учреждений сред. проф. образования / под ред. Т. И. Трофимовой. — М., 2014.

Интернет- ресурсы

1. www. fcior. edu. ru (Федеральный центр информационно-образовательных ресурсов).
2. wwww. dic. academic. ru (Академик. Словари и энциклопедии).
3. www. booksgid. com (Воокs Gid. Электронная библиотека).
4. www. globalteka. ru (Глобалтека. Глобальная библиотека научных ресурсов).
5. www. window. edu. ru (Единое окно доступа к образовательным ресурсам).
6. www. st-books. ru (Лучшая учебная литература).
7. www. school. edu. ru (Российский образовательный портал. Доступность, качество, эффективность).
8. www. ru/book (Электронная библиотечная система).
9. www. alleng. ru/edu/phys. htm (Образовательные ресурсы Интернета — Физика).
10. www. school-collection. edu. ru (Единая коллекция цифровых образовательных ресурсов).
11. https//fiz.1september. ru (учебно-методическая газета «Физика»).
12. www. n-t. ru/nl/fz (Нобелевские лауреаты по физике).
13. www. nuclphys. sinp. msu. ru (Ядерная физика в Интернете).
14. www. college. ru/fizika (Подготовка к ЕГЭ).
15. www. kvant. mccme. ru (научно-популярный физико-математический журнал «Квант»).
16. www. yos. ru/natural-sciences/html (естественно-научный журнал для молодежи «Путь в науку»).

 

17. Скачано с www.znanio.ru