Л/р № 2. Стрельба из баллистического пистолета по мишени.

Л/р № 2. Стрельба из баллистического пистолета по мишени.

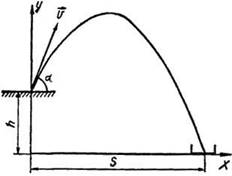
Цель работы: Стреляя из баллистического пистолета, установленного на столе, попасть, произведя только два выстрела, в картонную коробку, стоящую на полу – проверить тем самым формулы расчета тела, брошенного под углом к горизонту. 

Оборудование: баллистический пистолет; лабораторный штатив; коробка; измерительная лента или рулетка.

Вводная часть: Итак, целью работы является попадание в коробку-мишень, лежащую на полу, при стрельбе из

баллистического пистолета под углом к горизонту, закрепленном на столе (см. рис справа). Как узнать, на каком расстоянии должна находиться эта коробка-мишень?

Полет тела, брошенного под углом к горизонту (в нашем случае снаряда, выпущенного из баллистического пистолета), описывается следующими двумя уравнениями, позволяющими вычислить положение тела в любой момент времени t:

по горизонтали (вдоль пола): x = v₀t·Cosα; по вертикали (по высоте): y = v₀t·Sinα - gt²/2.

Запишем второе уравнение иначе, учтя, что g = 10 м/с², Sin45^o = 1/√2, а в момент падения  y = - h: 

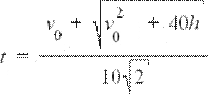gt²/2 - v₀t·Sinα - h = 0  или  

5t² - v₀t/√2 - h = 0.

Решив это квадратное уравнение относительно t, получим: 

Тогда дальность полета снаряда (S = x_max = v₀t/√2):  

Чтобы воспользоваться этими формулами, надо только придумать, как измерить начальную скорость v0 (скорость вылета снаряда из баллистического пистолета).   Скорость вылета снаряда можно узнать, если выстрелить вертикально вверх и заметить высоту, на которую поднимется снаряд, ибо Н = v₀²/2g. 

Ход работы.

Много лучше ход работы разработать самим, если вы поняли, как узнать начальную скорость снаряда, как рассчитать время полета и на каком расстоянии нужно установить коробку-мишень. 

1. Закрепите в нижней лапке штатива баллистический пистолет для стрельбы вертикально вверх под углом 90° к горизонту (см. рис. справа). 

Произведите предварительный выстрел из пистолета и заметьте, на какую приблизительно высоту поднимется снаряд.

Расположите на этом уровне свои глаза и передвиньте на этот уровень верхнее кольцо. 

Повторив выстрел, кольцо передвигают по вертикали так, чтобы выпущенный из пистолета снаряд достигал ровно края кольца. 

Измерив рулеткой или лентой расстояние от верхнего конца заряженного в пистолет снаряда до кольца, мы определим высоту подъема снаряда Н при стрельбе вверх. Повторите опыт 2—3 раза, каждый раз определяя высоту максимального подъема снаряда, и найдите ее среднее значение Н_ср. 

2.    По формуле высоты максимального подъема (Н_ср = v₀²/2g) определите квадрат начальной скорости вылета снаряда v₀² = 2gН_ср, а затем и саму скоростьv₀. 

3.    Закрепите в штативе баллистический пистолет у основания стола и установите его для стрельбы под углом 45^о. Измерьте рулеткой или измерительной лентой высоту h от пола до места установки снаряда баллистического пистолета (см. первый рис.)  По формуле дальности полета (используя найденные вами v₀ и h): 

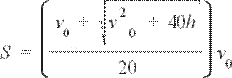
определите расстояние S от места выстрела до места падения снаряда для установки коробки (см. рис. выше), куда установите на полу центр коробки для попадания снаряда. Запишите подробно и аккуратно все ваши вычисления в отчет.

4.    Произвести выстрел под углом 45^о в направлении коробки (см. рис. выше). 

5.    Попадает ли снаряд в коробку? Если нет, проверьте свои расчеты и правильность установки баллистического пистолета, коробки и угла стрельбы. Покажите свои расчеты и результат стрельбы учителю. Сделайте вывод, подтверждаются ли формулы расчета движения тела, брошенного под углом к горизонту. Ответьте на контрольные вопросы. 

Контрольные вопросы:

1.    Как, используя приведенное выше уравнение вертикальной координаты полета тела  y = v₀t·Sinα - gt²/2, получить формулу расчета времени полета t?

о

2.    Как получить формулу дальности полета тела при выстреле под углом 45 , используя уравнение координаты x = v₀t·Cosα и времени полета t? Чему равно это время?

3.    Где можно использовать знания, полученные в ходе работы?

© 1975-2013. Н.В. Смирнов