Л/р № 3. Компьютерное моделирование стрельбы по мишени.

Л/р № 3. Компьютерное моделирование стрельбы по мишени.

Цель работы: Выбрав правильный угол для стрельбы, попасть выстрелом в цель, используя математическое моделирование полета снаряда; изучение зависимости дальности стрельбы от угла вылета снаряда.

Оборудование: компьютер, программа построения графиков функций (скачать с сайта http://www.webmath.ru/tests/podgotovkaegemath.php ), принтер, лист бумаги формата А4.

 Примечание: ВНИМАНИЕ! Используемая нами программа корректно работает только под Internet Explorer.

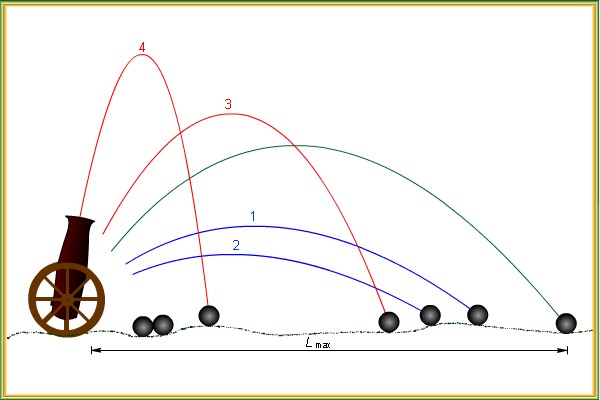
Посмотрите, как летит снаряд при различных углах выстрела из ствола  орудия.

Вводная часть:

Не столь трудно попасть в цель на расстоянии прямого выстрела, когда цель так близко, что снаряд не успевает существенно опуститься в полете под действием тяготения Земли. Особенно, если цель неподвижна. Военным же приходится решать, как правило, куда более сложные задачи. А если еще времени в обрез, когда или ты, или тебя!

В этой работе мы познакомимся с часто используемым приемом стрельбы, называемом "вилкой". Первый выстрел стараются сделать с небольшим запасом по высоте. Смотрят, куда попал снаряд, недолет или перелет. Допустим, у нас случился перелет. тогда следующий выстрел делают с поправкой, в нашем случае следует стрелять несколько ниже. Опять внимательно смотрят за результатом, допустим у нас получился недолет на такое же расстояние, каким был ранее перелет. Тогда надо ствол орудия поднять на половину нашей предыдущей поправки - и мы попадем точно в цель. Это называется "взять цель в вилку": перелет - недолет - в цель!  Такое попадание в цель всего в три снаряда доступно только очень опытным артиллеристам. Обычно приходится тратить больше, чем три снаряда. Во-первых, полет снаряда описывают тригонометрические функции синус и косинус, а они не являются линейными функциями, поэтому примененное нами выше слово "на половину", строго говоря, очень не точно. Во-вторых, на результат стрельбы влияет огромное количество случайных причин, бороться с которыми очень сложно. Поэтому наводчик орудия - бог, искусник, виртуоз. Иначе - гибель.

Попробуем себя в роли наводчика орудия. Поможет нам программа, умеющая строить графики функций. Мы будем задавать угол стрельбы, а она будет чертить нам траекторию вылетевшего под заданным нами углом снаряда. 

Теория вопроса.

Создадим вид функции, описывающей полет снаряда в поле тяготения Земли для нашего графопостроителя.

Полет снаряда во времени описывается известными уравнениями:

по вертикали (вдоль OY): y = v₀t·Sinα - gt²/2.

Для графика траектории нам следует выразить y через x. Выразим t через x из первого  уравнения t =x/(v₀·Cosα) и подставим его во второе, окончательно имеем: y = x·tgα - (g/2)·(x/v₀·Cosα)².

Не пугайтесь "страшной" формулы, за вас ее будет обсчитывать умная программа, поэтому еще немного терпения. Большинство математических редакторов и графопостроителей имеют свой синтаксис написания формул (свой язык). Поэтому в написании формулы кое-что придется чутьчуть изменить. В нашем случае тангенс следует писать как tan, а возведение в квадрат заменить на ^2.Перепишем формулу так, как это нужно программе: y=x·tanα - 5(x/(v₀·cosα))^2. 

Последнее и с формулой будет покончено. Выберем параметры стрельбы (ну, например):

начальная скорость вылета снаряда v₀= 200м/с. А угол α, под которым будет стрелять зададим о так. Это будет угол наибольшей дальности стрельбы (45 ) умноженный на некоторый переменный коэффициент k, который будем изменять так, чтобы снаряд в конце концов попасть в цель на расстоянии 3000 м. Нужно сказать, что α должно быть выражено в радианах: α = k·45^о = k·п/4. Или в обозначениях принятых в программе α = k*pi/4. Число k будем менять от 0 (наименьшая дальность) до 1 (наибольшая дальность), меняя тем самым угол вылета снаряда. Окончательно имеем:  

k = 1;

y=x tan(k*pi/4) - 5(x/(200 cos(k*pi/4)))^2

Вид формулы не должен нас смущать, ибо вставлять ее в графопостроитель мы будем копированием.

Графопостроитель.

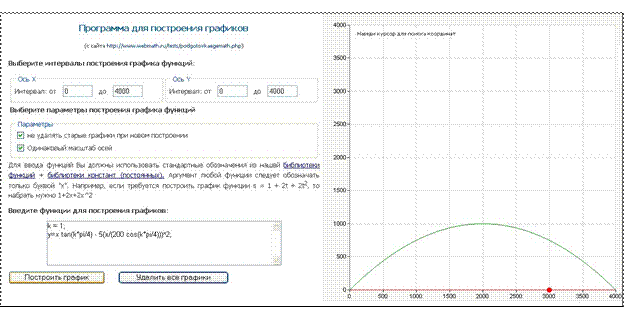
Перед началом работы следует запустить программу построения графиков и познакомиться с ней. Запустите программу. Рассмотрите рабочее поле программы, прочтите текст, расположенный в левой части окна. В правой будет вычерчен ваш график полета снаряда.Введите сразу нужные нам параметры. В поля "Ось Х" и "Ось Y" введите интервалы от 0 до 4000. В поле "Параметры" поставьте обе галочки: "не удалять старые графики при новом построении" и "Одинаковый масштаб осей".

Внизу сотрите все в поле "Введите функции для построения графиков" и нажмите кнопку "Удалить все графики". Перед началом работы справа должно быть чисто. В поле "Введите функции для построения графиков" копированием вставьте две строчки найденной нами функции, описывающей стрельбу по мишени:

k = 1;

y=x tan(k*pi/4) - 5(x/(200 cos(k*pi/4)))^2;

и нажмите кнопку "Построить график". Вы увидите результат нашего первого выстрела! 

Мы взяли для него наобум k = 1 или α = 45^о. И конечно промахнулись (перелет, попадание в отметку 4000 м)! Напоминаем, нас же интересует цель на отметке 3000 м.

Для учителя. Можно стрелять и с холма. Для этого в уравнение y добавьте высоту этого холма (например, + 100). Можно изменить и местоположение цели, сообщив ученикам устно ее координаты (например, дальность 3000 м, высота 500 м). Это полезно для того, чтобы ученики не слизывали друг у друга результаты.

Ход работы:

1. Итак, у нас получился перелет. Нам надо изменить угол стрельбы так, чтобы попасть в цель (отметка 3000 по горизонтали). Угол задает нам наше число k. Прямо в программе построения графиков измените значение k на другое, соблюдая синтаксис, принятый в этой программе (вместо запятой в дробном числе надо ставить точку, например, правильно будет написать  k = 0.65). Запишите новое k в свой отчет. Нажмите кнопку "Построить график". 2. Скорее всего, мы снова не попали в цель. Недолет или перелет? Введите новое значение k такое, чтобы следующий выстрел попал в цель. Запишите новое k в свой отчет.

Нажмите кнопку "Построить график".

3. Продолжайте выполнение пункта 2 до тех пор, пока не попадете совсем близко к цели. 4. Попав в цель, покажите результаты стрельбы учителю. Напечатайте ваши графики на принтере (Файл > Печать) или сохраните для отчета иным способом (например, картинкой левый Alt + PrintScreen, а затем вставить полученную картинку в Word и, сохранив, распечатать дома и вставить в отчет).

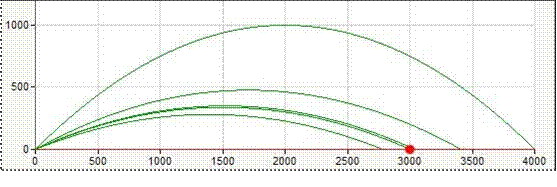
5. Сделайте вывод, каков характер зависимости дальности полета тела, брошенного под углом к горизонту, от угла вылета. Ответьте на контрольные вопросы. 

Контрольные вопросы:

1.    Из уравнений движения тела, брошенного под углом к горизонту:

по горизонтали (вдоль OX): x = v₀t·Cosα;

по вертикали (вдоль OY): y = v₀t·Sinα - gt²/2; выведите подробно вид зависимости y(x).

2.    Покажите, что между следующими записями существует соответствие всех элементов:

y = x·tgα - (g/2)·(x/v₀·Cosα)²; y =x tan(k*pi/4) - 5(x/(200 cos(k*pi/4)))^2.

3. Правильно ли утверждение, что чем больше угол стрельбы, тем дальше полетит снаряд?

© 1975-2013. Н.В. Смирнов