
Л/р № 4. Изучение закона сохранения импульса при упругом ударе шаров.
Цель работы: убедиться в справедливости закона сохранения импульса при упругом ударе шаров.
Оборудование: штатив, лоток, два шара одинаковой массы и шар большей массы, линейка измерительная, листы белой и копировальной бумаги, весы, разновес.
Введение: По закону сохранения импульса при любых взаимодействиях тел векторная сумма импульсов тел до взаимодействия равна векторной сумме импульсов тел после взаимодействия. В справедливости этого закона и нужно будет убедиться на опыте, исследуя столкновения шаров на установке, изображенной на рисунке справа.
 Шар, скатившись с
лотка, движется по параболе до удара о поверхность стола. Горизонтальные
составляющие скорости шара и его импульса во время свободного падения не
изменяются, так как нет сил, действующих на этот шар в этом направлении. Затем
на краю лотка ставят второй шар и запускают первый шар точно таким же образом,
как и в первом опыте. После соударения в горизонтальном направлении слетают с
лотка оба шара. При этом часть импульса движения первого шара передается
второму. По закону сохранения векторная импульса сумма импульсов первого р1
и второго р2 шаров до столкновения должна быть равна сумме импульсов
этих шаров после столкновения.
Шар, скатившись с
лотка, движется по параболе до удара о поверхность стола. Горизонтальные
составляющие скорости шара и его импульса во время свободного падения не
изменяются, так как нет сил, действующих на этот шар в этом направлении. Затем
на краю лотка ставят второй шар и запускают первый шар точно таким же образом,
как и в первом опыте. После соударения в горизонтальном направлении слетают с
лотка оба шара. При этом часть импульса движения первого шара передается
второму. По закону сохранения векторная импульса сумма импульсов первого р1
и второго р2 шаров до столкновения должна быть равна сумме импульсов
этих шаров после столкновения.
—> —> —> —>
р1 + р2 = р'1 + р'2 (1)
Если оба шара после столкновения движутся вдоль одной прямой и в том же направлении, в каком двигался первый шар до столкновения, то от векторной формы записи закона сохранения импульса можно перейти к алгебраической форме:
р1 + р2 = р'1 + р'2,
так как p = mv, то
m1v1+ m2v2 = m1v'1 + m2v'2 (2)
Заметим, что скорость второго шара v2 до столкновения равна нулю.
Для проверки выполнения равенства (2) необходимо измерить массы шаров m1 и m2 с помощью весов, а также найти способ узнать скорости шаров v1, v'1, v'2.
Так как во время свободного падения шара по параболе горизонтальная составляющая его скорости не изменяется, она может быть найдена так:
v = ℓ/t (3),
где ℓ - дальность полета шара в горизонтальном направлении, а t - время его свободного падения, равное t = √(2h)/g.
В равенстве (3) заключена важная мысль: v и ℓ прямо пропорциональны друг другу, а значит по длине ℓ можно судить о величине горизонтальной скорости! Этим и воспользуемся в данной работе.
Ход работы:
ЧАСТЬ I. Исследование центрального удара.
1. Используя весы, измерьте массы шаров m1 и m2. 2. Заготовьте таблицу для записи результатов:
|
|
|
До удара |
После удара |
|
|
Шар № |
1 |
|
1
|
2 |
|
Масса шара m, (кг) |
m1 = |
|
-
|
- |
|
Дальность полета ℓ, (м) |
ℓ1= |
|
ℓ'1= |
ℓ'2 = |
|
Высота падения шаров h, (м) |
h = |
|
|
|
|
Время полета t, (с) |
t = |
|
|
|
|
Горизонтальная скорость v, (м/с) |
v1 = |
|
v'1 = |
v'2 = |
|
Импульс р, (кг·м/с) |
р1 = |
|
р'1 = |
р'2 = |
|
Сумма импульсов Σр, (кг·м/с) |
Σр = р1 + р2 = |
Σр' = р'1 + р'2 = |
||
2. Укрепите лоток в лапке штатива таким образом, чтобы горизонтальная часть лотка находилась на высоте 20 см от стола. На столе перед лотком положите лист белой бумаги.
3. Возьмите шар с большей массой, установите его у верхнего края наклонной части лотка. Сделав несколько пробных пусков, определите с какой высоты надо пускать шар, чтобы место его падения было в районе второй половины листа, но чтобы он ни в коем случае не ударялся за пределами листа. Отметьте это положение на лотке. На лист белой бумаги положите лист копировальной бумаги.
4. Отпустите шар с края лотка без начальной скорости, чтобы получить отметку падения шара по вертикали.
5. Отпустите шар с намеченной вами отметки на лотке и по отметке на листе белой бумаги определите его дальность полета в горизонтальном направлении. Опыт повторите 3 раза и найдите среднее значение дальности полета ℓ1 (см. рис. выше). Запишите это значение ℓ1 в лист отчета.
6. Зная высоту края лотка h над столом, вычислите время падения шара t, затем горизонтальные составляющие его скорости v1 и импульса р1. Запишите свои вычисления в отчет.
7. Установите на краю горизонтальной части лотка второй шар и осуществите запуск первого шара с той же высоты лотка, как в первом опыте. По отметкам на бумаге найдите дальности полетов шаров в горизонтальном направлении после их столкновения. Опыт повторите три раза и найдите среднее значение дальности полета первого шара ℓ'1 и дальности полета второго шара ℓ'2 (рисунок выше) По найденным числовым значениям дальностей полетов ℓ'1 и ℓ'2 вычислите числовые значения скоростей шаров после столкновения v'1 и v'2 и их импульсов р'1 и р'2. Запишите полученные результаты в отчет.
8. Сравните импульс первого шара до столкновения р1 с суммой импульсов двух шаров после столкновения р'1 + р'2.
9. Сделайте вывод. Ответьте на контрольные вопросы.
ЧАСТЬ II. Исследование нецентрального удара.
1.
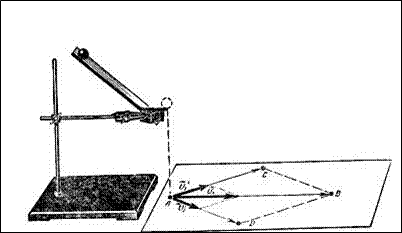 Возьмите два шара одинаковой массы. Один шар установите на
краю лотка таким образом, чтобы вектор скорости первого шара при столкновении
был направлен мимо центра второго шара. При таком столкновении, называемом
нецентральным, векторы скорости шаров после столкновения v'1 и v'2
имеют различные направления. По закону сохранения импульса должно выполняться
векторное равенство:
Возьмите два шара одинаковой массы. Один шар установите на
краю лотка таким образом, чтобы вектор скорости первого шара при столкновении
был направлен мимо центра второго шара. При таком столкновении, называемом
нецентральным, векторы скорости шаров после столкновения v'1 и v'2
имеют различные направления. По закону сохранения импульса должно выполняться
векторное равенство:
—> —> —>
m1v1 = m1v'1 + m2v'2,
а так как m1 = m2, то
—> —> —> v1 = v'1 + v'2.
2. Для проверки последнего равенства получите отметки падения шара по вертикали с края лотка (точка А), точки падения шара после свободного скатывания (точка В) и точек падения шаров после нецентрального столкновения (точки С и Д) (рисунок справа).
3. Соедините точку А с точками В, С и Д. Вектор АВ параллелен вектору скорости v1 шара и пропорционален ему по длине. Векторы АС и АД параллельны векторам скорости v'1 и v'2 после их столкновения. При выполнении закона сохранения импульса сумма векторов АД и АС должна быть равна вектору АВ.
4. Постройте параллелограмм со сторонами АД и АС и проведите его диагональ из вершины А. Сравните эту диагональ с вектором АВ. Напишите на листе с отметками падения шаров и вашими построениями свои фамилии, класс и вложите его в свой отчет.
5. Оцените границы погрешностей выполненных измерений. Сделайте вывод.
Контрольные вопросы:
1. Что называется импульсом тела?
2. При каких условиях выполняется закон сохранения импульса?
3. Выходят ли обнаруженные в опыте отклонения от закона сохранения импульса за пределы границ погрешностей измерений?
© 1975-2013. Н.В. Смирнов
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.