Материалы по физике

             Волна де Бройля

Из предыдущих разделов физики нам известно, что такие процессы природы, как тепловое и рентгеновское излучения, фотоэффект и др., хорошо объясняются на основе использования корпускулярных пред- ставлений. С другой стороны, интерференция, дифракция, поляриза- ция света объясняются на основе волновых представлений, согласно которым свет есть электромагнитные волны. Таким образом, свет, в широком понимании этого слова, представляет своеобразное сочета- ние волновых и корпускулярных свойств материи. В одних условиях эта материя наиболее четко проявляет волновые свойства, в других – корпускулярные. Одним из критериев применимости того или иного подхода является величина поперечного сечения цуга волн: если по- перечное сечение цуга волны сравнимо с размерами частиц вещества, то свет, электромагнитная волна проявляют корпускулярные свойства и электромагнитное излучение можно рассматривать как поток свето- вых частиц, если же поперечное сечение цуга волн значительно боль- ше размера частиц, то свет следует рассматривать как поток электро- магнитной волны.

Таким образом, свет как материя обладает двойственной природой. Пусть на границу раздела двух сред падает плоская электромагнит-

ная волна.

Рис. 1.1.1. Изменение скорости частицы у поверхности раздела сред без учета преобразования полей

Из рис. 1.1.1 следует, что v_1x = v_2x или

v sin i

= v sin i ;

n = c , n

= c ;

sin i 1

= v1  =  n 1 . = 1 ,

1              1           2

2              1                       2

1                        2

sin i  2     v2   n 2                  n

n = n 2 – абсо-

n 1

лютный показатель преломления, i₁, i₂ – углы падения и преломления. Применив корпускулярный подход, мы получили закон, обратный закону преломления. Таким образом, хотя для оптических явлений корпускулярный подход применим, но он дает неверный результат. Причина несоответствия корпускулярной теории опыту состоит в том, что для описания этого процесса необходим иной подход, при кото- ром учитываются взаимодействия множества световых частиц с ато- мами вещества. Математической основой описания такого процесса

является кинетическое уравнение переноса.

В 1923 г. французский ученый де Бройль высказал предположение, что двойственная природа материи должна проявляться не только у электромагнитного излучения. Он предположил, что электроны при определенных условиях должны проявлять волновые свойства. Он писал: "В оптике в течение столетия слишком пренебрегали корпус- кулярным способом рассмотрения явлений по сравнению с волновым. Не делалось ли в теории материи обратной ошибки? Не думали ли мы слишком много о картине частиц и не пренебрегали ли чрезмерно кар- тиной волн?" В 1929 г за эту работу ему была присуждена Нобелев- ская премия.

Де Бройлю было 30 лет, когда он высказал свою гипотезу о волно- вых свойствах материи и вывел формулу, с помощью которой можно вычислить длину волны, связанную с движущимся электроном. К мысли о том, что электрон должен обладать волновыми свойствами, де Бройля привели следующие факты и соображения. В природе су- ществует аналогия между геометрической оптикой и механикой. Ос- новные законы этих двух разделов физики можно сформулировать в тождественно математической форме. Это значит, что вместо того чтобы рассматривать движение заряженной частицы в электрическом

поле с потенциалом

j(r ) , можно рассматривать распространение по-

тока частиц в пространстве с абсолютным показателем n(r ) .

Заметим, что рассматриваемая аналогия в настоящее время охва- тывает все разделы физики и в ряде случаев бывает очень полезной. Покажем это на конкретном примере.

Допустим, имеется две контактирующие между собой среды. По- тенциал электрического поля в верхней среде φ₁, а потенциал в ниж-

ней среде φ₂. На границе раздела происходит постепенное изменение потенциала. Тогда напряженность электрического поля в пограничном слое можно представить в виде (см. рис. 1.1.2):

r      dj r       r

Если φ₁> φ₂ ,

E = -

dy

j = Ey j.

dj <

r      r,

0,   E ­­ j

dy

и в пределах пограничного слоя на электрон будет действовать сила

Fy = eE,

e < 0,

направленная вниз, а в направлении координатной оси 0Х сила дейст- вовать не будет, так как E_x=0. Следовательно,

F1x  = F2 x  = 0,

sin i1

sin i2

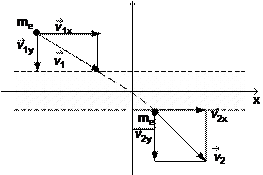y

v1x = v2 x ;

= v2 .

v1

Fy ­¯ j.

(1.1.1.)

Рис. 1.1.2. Изменение скорости частицы у поверхности раздела сред с учетом преобразования полей

Электрон, проникая в пространство с потенциалом φ₁, приобретает кинетическую энергию

m v²

k1 = e 1 = eDj1

2

Тогда в пространстве с потенциалом φ₂ его кинетическая энергия будет

Значит,

m v²

k2 = e 2 = eDj 2.

2

1

v2 ⎛ Dj2 ⎞ 2

(1.1.2)

Подставляя полученное выражение (1.1.2) в (11.1.), имеем:

1

sin i1

sin i 2

⎛        ⎞

⎜ Dj 1 ⎟

(1.1.3)

⎝        ⎠

Формула (1.1.3) является математической записью закона прелом- ления в электронной оптике.

Закон преломления в геометрической оптике формулируется в виде

n   = n 2 = sin i 1 .

(1.1.4)

1

sin i 2

Из сравнения выражений (1.1.3) и (1.1.4) можно получить относи- тельный показатель преломления в электронной оптике:

1

⎛ Dj2 ⎞ 2

(1.1.5)

n21 = ⎜ Dj ⎟

⎝     1 ⎠

В случае электромагнитных волн плоская электромагнитная волна представляет собой пучок параллельных лучей, для которых волновой фронт – плоскость, перпендикулярная направлению распространения лучей, а волновая поверхность – система параллельных поверхностей

с колебаниями векторов E и H в одной и той же фазе

r                            r     r

r          2p  r    r

E = E0 cos(wt - k x) × j ,

H = H 0 cos(wt - k x) × k ,

k = l , k = r .

Однако, если принять корпускулярную точку зрения, то плоскую электромагнитную волну можно рассматривать как поток световых частиц, перемещающихся в пространстве параллельно (рис. 1.1.3) или даже связать ее с отдельно движущимся фотоном.

Если в пространстве существует поток свободных, не взаимодей- ствующих между собой электронов (на эти электроны не действуют внешние силы), то в таком потоке электроны должны перемещаться параллельно. Эта картина верна, если пользоваться корпускулярными представлениями. Но если воспользоваться волновыми представле- ниями, т.е. применить понятие волны материи, то с таким потоком частиц можно связать некий волновой процесс, и описание движения электронов с волновой точки зрения должно быть аналогично описа- нию плоской электромагнитной волны. Следовательно, такой волно- вой процесс также можно изобразить в виде плоской волны. Поэтому де Бройль предположил, что между волновыми и корпускулярными

характеристиками электрона должна существовать точно такая же взаимосвязь, как и между соответствующими характеристиками фо- тона. И, кроме того, де Бройль предположил, что корпускулярное опи- сание движения свободного электрона должно быть подобно корпус- кулярному описанию фотона, волновое описание свободного электро- на должно быть подобно волновому описанию потока фотонов в элек- тромагнитной волне (рис. 1.1.3).

mф   c

mф   c

mф   c

фотоны

y                                                                 y

E E E

фронт                                                                                                                               x

волны

E = E0 cos(w t - k x) × j

j = j0 cos(wt - k x)

а                                                    б

Рис. 1.1.3. Модель плоской волны для фотонов (а)

и для электронов (б)

По определению импульс фотона и энергия фотона соответственно равны

Значит,

pф = mф c,

e = mф

c² = pф с,

e = hn,

ν = c .

l

p      e    hn     h             h

(1.1.6)

ф = c =  c   =  l ;    pф  = l ,

где λ – длина электромагнитной волны, h – постоянная Планка, p_ф – импульс фотона. Таким образом, уравнение (1.1.6) связывает между собой как корпускулярные, так и волновые характеристики света во- едино, а коэффициентом связи является постоянная Планка.

Де Бройль предположил, что уравнение (1.1.6) можно применять не только для фотонов, но и для электронов. А так как импульс элек- трона p_e=p=m_ev, то длина волны некоторого волнового процесса, свя- занного с движущимся электроном, будет определяться из уравнения

p = h  = m v.

l       e

Отсюда

И если

l =

mev²

h .

mev

K =         = eU £ 10 кэВ, 2

то масса электрона m_e = m₀, т.е. практически не отличается от массы покоя. Тогда в соответствии с законом сохранения энергии можем за- писать:

mev²

1

⎛ 2eU ⎞ 2

(1.1.7)

eU =

;   v = ⎜        ⎟ . 2               ⎝ me ⎠

После подстановки найденного выражения для скорости имеем

⎛ 2eU ⎞ 2

или

m⎜        ⎟

⎝  me ⎠

U 2

м = 12,3 Å, [U]=В.

Пусть U = 100 B. Тогда  λ = 0,12  нм.  Если  же  U = 10000  B,  то  λ= 0,012 нм.

Таким образом, длина волны свободного электрона, двигающегося со скоростью v, соответствует длине волны рентгеновского излучения. На это обстоятельство мы обратим внимание в дальнейшем. Такое совпадение, разумеется, носит случайный характер.

Скачано с www.znanio.ru