НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ ПРОЕКТ на тему: «Волшебный циркуль» НАПРАВЛЕНИЕ: черчение

НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ ПРОЕКТ

на тему:

«Волшебный циркуль»

НАПРАВЛЕНИЕ: черчение

2020 г

Аннотация

Тема исследовательской работы: «Волшебный циркуль»

Цель исследовательской работы: изучить многообразие аспектов использования циркуля в различных областях жизнедеятельности человека, убедиться в необходимости такого простого инструмента, как циркуль.

Теоретическая значимость исследования определяется тем, что рассмотрены виды циркулей, а так же структурированы способы работы с ним.

Практическая значимость исследования состоит в разработке творческих упражнений и заданий, для того чтобы показать, как многое в нашей жизни связано с циркулем.

Этапы исследования: выбор темы, постановку цели и задач, сбор материала, обобщение полученных данных, подготовку проекта, подведение итогов работы.

Новизна исследования: в последнее время существует проблема использования циркуля на уроках, и крайне узкое восприятии возможностей этого чудо - устройства. Каждый с малых лет должен знать о циркуле, о его важности и безграничных возможностях. Изучая историю циркуля и его применение в различных областях повседневной жизни, мы не только совершенствуем предметные знания, но и узнаем новые и необычные сведения из истории мировой культуры, что способствует общему развитию каждого человека.

Результат исследования:

1. Мини-презентация «Волшебный циркуль».

2. Выпуск брошюры «Волшебный циркуль» с творческими заданиями на построение.

План проведения проекта

Подготовка к проекту

·         Формулирование темы проекта, его целей, задач.

·         Составление учителем визитки проекта, методических и дидактических материалов к проекту.

Реализация проекта

·         Знакомство с проектом (вводная презентация), формулирование проблем, которые будут решаться в проекте.

·         Обсуждение плана работы учащихся.

·         Обсуждение возможных источников информации.

·         Работа учащихся по выполнению заданий практических работ.

Оформление результатов проектной деятельности

·         Оформление результатов исследования в форме брошюры.

·         Оформление приложений.

Защита проекта

·         Защита проекта. Самооценка.

·         Оценивание работы по проекту участниками, учителем.

Исследовательская работа носит культурологический и творческий характер и будет интересна различной категории учащихся.

Содержание

Введение ……………………………………...……............................……….5

I.История циркуля ………………................................................…………….7

1.1. Кто придумал циркуль ………….........................…........................7

1. 2. Первые железные циркули..............................................................8

II. Современные циркули............….………………...........................………..9

2.1. Основные виды циркулей...........…………..............................……9

2. 2. Циркули в медицине......................................................................11

2.3. Циркуль в навигации и картографии.............................................11

2.4. Циркули на производстве...............................................................12

III. Геометрические построения с помощью циркуля..................................14

3.1. Простейшие задачи на построение................................................14

3.2. Построение правильных многоугольников..................................15

3.3. Построения с помощью одного циркуля ………….....................17 IV. Необычные назначения циркуля……………………..............................19

V. Интересные факты о циркуле…………………………………………….20

VI. Применение циркуля в творческой деятельности……………………..22

VII. Способы решения стереометрических задач………………………….23

Заключение …………………………………………………......................…25

Список используемой литературы………………………….........................26

Введение

Листая учебник черчения на первом уроке, я увидел необычные иллюстрации с окружностями и многоугольниками, вписанными в них. Меня заинтересовали построения с помощью циркуля и сама история этого инструмента. Когда я ввел в поисковой строке Яндекса слово «циркуль», то оказалось, что это не только измерительный инструмент, но и маленькое созвездие Южного полушария. А различные виды циркулей применяют в картографии, навигации, медицине, на производстве. Изображения циркуля присутствует на гербах и на монетах. Циркуль заинтересовал меня, и свою работу я посвящаю истории происхождения циркуля и возможностям его применения. В центре моего внимания находятся вопросы, связанные с первыми упоминаниями о циркуле, видами циркулей, применением циркулей в различных областях науки и культуры. Значительное внимание я уделил решению геометрических задач с помощью циркуля и линейки, созданию рисунков и узоров.

На мой взгляд, выбранная тема очень интересна и актуальна, ведь мы используем циркуль во многих науках. Он знаком каждому человеку со школы - на уроках черчения и геометрии нельзя обойтись без этого инструмента для построения окружностей и дуг, на уроках географии для измерения расстояний. С циркулем можно встретиться и на уроках истории при изучении гербов и символов. А построения с помощью циркуля и линейки развивают пространственное воображение и помогают развить логику мышления. Для многих учеников черчение и математика – достаточно «сухие» науки, а если изучать их как часть общечеловеческой культуры, рассматривая исторические сведения, красоту, гармонию и применение чертежных понятий и инструментов в повседневной жизни, то предмет станет «живым», интересным и любимым для каждого ученика.

Таким образом, у меня возникла гипотеза:

Предполагаю, что циркулем можно не только рисовать и создавать интересные узоры, но и решать геометрические задачи. Работа с циркулем - завораживающий процесс и в этом случае вообще не имеет никакого значения, умеете ли вы рисовать и фантазировать! Главное, знать, что такое циркуль, как он работает и иметь желание творить. И удовольствие будет гарантировано!

Цель исследования:

изучение многообразия аспектов использования циркуля в различных областях жизнедеятельности человека.

Задачи исследования:

1) отправиться в историческое путешествие создания циркуля;

2) определить основные области применения циркуля как

инструмента;

3) исследовать значение изображения циркуля, отыскать

интересные факты о циркуле;

4) оценить возможности применения циркуля в творческой

деятельности и при решении задач на построение.

Объект исследования: циркуль обыкновенный.

Предмет исследования: аспекты использования циркуля в различных областях жизнедеятельности человека.

Методы исследования:

Наблюдение, сравнение, анализ, творческая и аналитическая деятельность, использование справочной и учебной литературы, Интернет-ресурсов.

I. История циркуля

Слово «циркуль» происходит от латинского circulus - «круг, окружность,  кружок», от латинского же circus - «круг, обруч, кольцо». В русский язык циркуль или «циркул» пришел от польского cyrkuɫ или немецкого Zirkel.

1.1. Кто придумал циркуль

Персонаж древнегреческой мифологии, Дедал, был потомком царя Эрехфея. Он считался искусным строителем, художником и изобретателем. Согласно легенде, к числу изобретений Дедала относятся основные столярные инструменты: рубанок, отвес, клей.

У Дедала в Афинах жил племянник по имени Талос, очень талантливый юноша. Когда Талосу исполнилось всего 12 лет, он придумал гончарный круг, с помощью которого люди стали изготовлять посуду. Скелет рыбы навел его на мысль сделать первую на свете пилу. Дядя Талоса позавидовал его таланту и, улучив момент, столкнул юношу с городского вала. Но до этого Талос успел одарить людей еще одним изобретением. Он соединил с помощью шарнира два одинаковых по длине стержня — так получился циркуль¹.

2.2. Первые железные циркули

На стенах и куполах храмов и домов, на резных чашах и кубках древних Вавилонии и Ассирии нарисованы такие правильные круги, что без циркуля их просто невозможно провести. А существовали эти государства около 3 тысяч лет назад. Самый старый циркуль, дошедший до нас уже не из легенды, а из реальности. Железный циркуль нашли во Франции при раскопках древнего кургана. Он пролежал в земле более 2 тысяч лет².

Во время раскопок в Помпеях было найдено много древнеримских бронзовых циркулей. Причем в Помпеях найдены инструменты уже совсем современные: циркули с загнутыми концами для измерения внутренних диаметров предметов, «кронциркули» для измерения максимального диаметра, пропорциональные - для кратного увеличения и уменьшения размеров.

При раскопках в Новгороде был найден стальной циркуль-резец для нанесения орнамента из мелких правильных кружочков, очень распространенного в Древней Руси.

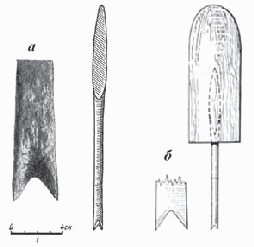
Стальной циркуль-резец

Костяные гребни с циркульным орнаментом.

Таким образом, судя по давности изображений, которые невозможно выполнить без некоего подобия циркуля, этому инструменту более 3 тысяч лет. И использовался он в основном для нанесения орнаментов.

II. Современные циркули.

2.1. Основные виды циркулей

Со временем конструкция циркуля практически не изменилась, но ему придумали массу насадок, так что теперь он может вычерчивать окружности радиуса от 2 миллиметров до 60 сантиметров,  кроме того, обычный графитный грифель можно заменить насадкой с рейсфедером для черчения тушью.

Есть множество типов циркулей. Одни из них: разметочный или делительный, его применяют для снятия и перенесения линейных размеров.

Разметочный циркуль Делительный циркуль для наружных измерений

Чертежный или круговой циркуль применяют для вычерчивания окружностей диаметром до 300 миллиметров.

Пропорциональный циркуль применяют для изменения масштабов снимаемого размера.

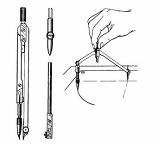
Чертёжный циркуль. Круговой циркуль. Пропорциональный циркуль.

2.2. Циркули в медицине

Циркуль используется не только в черчении - применение ему нашлось и в медицине: например, большой и малый толстотные циркули применяются для измерения поперечных размеров тела человека и для измерения размеров черепа. А циркуль-калипер используется для измерения толщины подкожно-жировой складки.

Циркуль-калипер

Также известен циркуль Вебера, немецкого психофизиолога и анатома, разработанный им для определения порога кожной чувствительности.

Эрнст Вебер

2.3. Циркуль в навигации и картографии

Используемый для измерения расстояния на карте, циркуль-измеритель обычно делают из меди со стальными кончиками. Для того чтобы отмечать и измерять расстояния на карте, яхтсмену понадобятся пара измерителей и циркуль. Желательно что бы они были лучшего качества - медные или из нержавеющей стали. Высота измерителей должна быть не менее 15 см, чтобы они широко раздвигались. Управляемый одной рукой циркуль, который имеет согнутый верх, легче в использовании, чем неизогнутый, который требует две руки, чтобы открыть и закрыть его. Чтобы воспользоваться штурманским циркулем-измерителем, надо взять его так, как показано на рисунке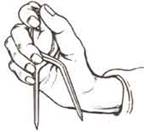 

Яхтсмену надо открыть циркуль в растворе, подходящем к замеряемой площади, затем определить расстояние, используя шкалу широты карты. Если раствор циркуля недостаточно широк, установить его на подходящую ширину.

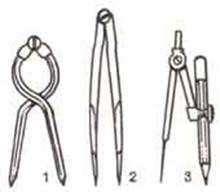
  Штурманский (1) и простой (2) измерители и циркуль (5)

2.4. Циркуль на производстве

Циркуль для разметки радиусов от центров готовых отверстий диаметром 10-50 мм с применением шаровых вставок изготовил новатор В. В. Соколов.³ В одной ножке стандартного циркуля высверливается отверстие диаметром 5 мм, куда вставляются цилиндрические наконечники шаровых вставок. Максимальный радиус разметки 240 мм. Такая конструкция циркуля дает возможность производить разметку радиусов от отверстий (цилиндрических и нецилиндрических) на плоскостях, расположенных под различными углами к оси отверстия.

Применение циркуля с шаровыми вставками экономит на операциях разметки до 25% вспомогательного времени, заметно облегчает труд рабочего.

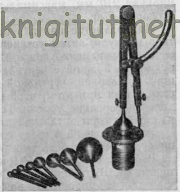
Циркули предназначены и для резки окружностей различных диаметров.  Данный инструмент предлагается в различных модификациях, в зависимости от непосредственной поставленной задачи. Циркули, которые не имеют масляный резервуар необходимо смачивать в масле, чтобы производить качественный разрез и не допускать быстрый износ инструмента.

Так выглядит циркуль для резки стекла с шестью роликами, длина резки примерно 10 000 метров, минимальный диаметр окружности - 85мм, максимальный - 2000мм:

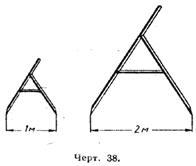
Расстояния на сельскохозяйственных полях можно измерять с помощью полевого циркуля. Расстояние между ножками полевого циркуля делается или 1 м, или 2м.

Таки образом, очевидно значительное расширение областей применения циркуля: от инструмента для нанесения кругового орнамента до инструмента для измерения и разметки в медицине, навигации и картографии, на производстве.

III. Геометрические построения с помощью циркуля

Чаще всего циркуль используют на уроках геометрии. Особенно интересны задачи на построения с помощью циркуля и линейки. Рассмотрим некоторые из них.

3.1. Простейшие задачи на построение

Построение угла, равного данному

Отложить от данного луча в данную полуплоскость угол, равный данному углу.

1

Построение.

Проведем окружность с центром в вершине данного угла. Пусть B и C – точки пересечения окружности со сторонами угла. Радиусом AB проведем окружность с центром в точке A₁ – начальной точке данного луча. Точку пересечения этой окружности с данным лучом обозначим B₁. Проведем окружность с центром в точке B₁ и радиусом BC. Точка пересечения C₁ построенных окружностей в указанной полуплоскости лежит на стороне искомого угла.

2

Проведение прямой, параллельной данной

Через заданную точку A провести прямую, параллельную данной прямой a.

Построение.

Через заданную точку A и произвольную точку B прямой a проведем прямую AB. Пусть C – произвольная, отличная от B точка прямой a. Построим от луча AB в полуплоскость, не содержащую точку C, угол, равный углу ABC. Пусть AD – сторона построенного угла. Тогда прямая AD || a.

Доказательство следует из признака параллельности прямых (теорема 3.1), ввиду равенства углов (ABC) и (BAD) как внутренних накрест лежащих при прямых a, (AD) и секущей (AB).

1

3.2. Построение правильных многоугольников

Построение правильного шестиугольника и треугольника.

Сторона правильного шестиугольника равна радиусу R описанной окружности. Поэтому, для построения правильного шестиугольника, достаточно построить окружность, взять на ней произвольную точку А и, не меняя раствора циркуля, отметить на этой окружности последовательно точки B, C, D, E, F так, чтобы AB=BC=…=EF. Проведя затем отрезки AB, BC, CD, DE, EF, FA, получим шестиугольник ABCDEF, который является правильным.

Для того, чтобы построить правильный треугольник нужно соединить точки данного шестиугольника через одну, значит соединим точки A,C и E. Треугольник ACE- искомый.

Построение правильного четырехугольника и восьмиугольника.

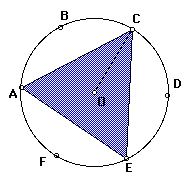
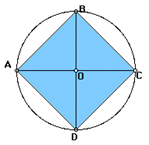
Пусть дана окружность с центром в точки О и радиусом R. Через точку О проведем диаметр АС и к этому диаметру проведем серединный перпендикуляр, который пересечет окружность в двух точках В и D. Теперь последовательно соединим точки A,B,C и D. ABCD-искомый квадрат.

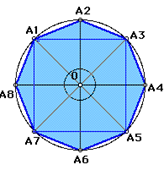
Для того, чтобы построить правильный восьмиугольник нужно сначала построить правильный четырехугольник, например, А₁А₃А₅А₇-квадрат, потом построить биссектрисы углов А₁OА₃, А₃OА₅, А₅OА₇, А₇OА₁, которые пересекут окружность в точках А₂, А₄, А₆, А₈ соответственно, затем последовательно соединить точки А₁,А₂,А₃,А₄,А₅,А₆,А₇,А₈. А₁А₂...А_{8 .} Получим восьмиугольник.

3.3. Построения с помощью одного циркуля.

Задача 1.

а) Постройте с помощью одного циркуля отрезок, который в два раза длиннее данного отрезка.
б) Постройте с помощью одного циркуля отрезок, который в n раз длиннее данного отрезка.

Решение:

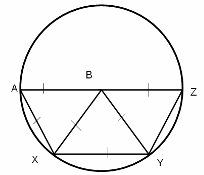
а) Пусть AB — данный отрезок. Проведем окружность с центром B радиуса AB. Отложив на этой окружности хорды AX, XY и YZ, равные по длине AB, мы получим равносторонние треугольники ABX, XBY и YBZ. Поэтому ABZ = 180^o и AZ = 2AB.

б) В решении задачи а) описано, как на прямой AB отложить отрезок BZ, равный AB. Повторив эту процедуру n - 1 раз, получим отрезок AC, причем AC = nAB.

Задача 2.

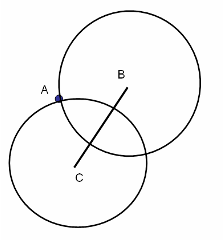
Постройте с помощью одного циркуля точку, симметричную точке A относительно прямой, проходящей через данные точки B и C.

Решение:

Проведем окружности с центрами B и C, проходящие через A. Тогда отличная от A точка пересечения этих окружностей и будет искомой.

Задача 3.

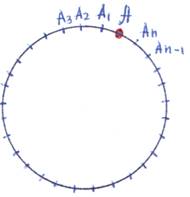
Разделите окружность с данным центром на 6 равных частей, пользуясь только циркулем.

Решение:

Возьмём на окружности радиуса R произвольную точку A. С центром в этой точке проведём окружность радиуса R. Пусть B и C — точки пересечения окружностей. С центрами в этих точках проведём ещё две окружности радиуса R. Пусть D и E — отличные от A точки пересечения этих окружностей с данной. С центром в точке D проведём ещё одну окружность радиуса R. Обозначим через F отличную от B точку пересечения этой окружности с данной. Докажем, что точки A, B, D, F, E и C делят данную окружность на 6 равных частей.

В самом деле, если O — центр данной окружности, то все стороны треугольников AOB, BOD, DOF, FOE, EOC и AOC равны R. Значит, эти треугольники равносторонние. Следовательно,

AOB = BOD = DOF = FOE = EOC = AOC = 60^o,

а это означает, что построенные точки делят окружность на 6 равных частей.

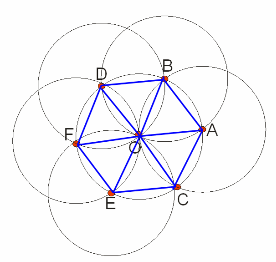
Таким образом, можно сделать вывод, что циркуль и линейка это неотъемлемые инструменты при решении задач на построение. А задачи на построений с помощью только одного циркуля – увлекательная и развивающая игра воображения.

IV. Необычные назначения циркуля

У китайцев циркуль означает правильное поведение. Циркуль - атрибут Фо-хи, легендарного китайского императора, считавшегося бессмертным. Сестра Фо-хи имеет квадрат, и вместе они - мужской и женский принципы, гармония инь и янь.

Циркуль, совмещенный с наугольником (название «наугольник» принадлежит старинному измерительному инструменту, шаблону для построения наиболее употребляемых углов в столярном деле и строительстве) - одна из самых распространенных эмблем, символов и знаков масонов. На этой эмблеме циркуль символизирует Небесный Свод, а наугольник - землю. Небо в данном случае символически связано с местом, где чертит план Великий Строитель Вселенной. Буква «G» в центре в одном из значений - сокращение слова «геометр», используемого в качестве одного из названий верховного существа⁴.

На купюре 50 германских марок выпуска 1989 г., рядом с портретом немецкого архитектора Бальтазара Неймана (1687–1753) помещено изображение пропор­ционального циркуля – основного инструмента зодчего тех времен⁵.

На памятной монете 2000 г., посвящённой С.В. Ковалевской, циркуль символизирует математику.

Кроме того, циркуль является символом неуклонной и беспристрастной справедливости, совершенной фигурой круга с центральной точкой, источником жизни.

V. Интересные факты о циркуле

Ц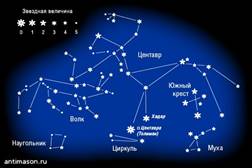иркуль в космосе

Циркуль - не только всем известный инструмент. Этим словом названо маленькое созвездие южного полушария к западу от «Наугольника» и «Южного треугольника», рядом с α-Центавра.

Созвездие Циркуль (Circinus) совершенно не примечательное. Оно новое и введено в обиход французским астрономом Луи Лакайлем в числе прочих других, когда он попытался упорядочить большие массивы звезд вблизи южного полюса. Особой фантазии при этом Лакайль не проявлял, и потому большинство созвездий, введенных им, носят весьма прозаические названия инструментов или навигационных приборов: Наугольник, Телескоп, Микроскоп, Октант, Компас… Созвездие состоит из очень тусклых звезд; в нем нет звезд ярче 4-й звездной величины. При хорошей видимости в ясную и безлунную ночь в созвездии Циркуля можно разглядеть невооруженным глазом около двадцати звезд. Они расположены хаотично и не образуют никакой характерной геометрической фигуры. Даже имея богатое воображение, в них нельзя увидеть изображение циркуля. Поэтому на старинных звездных картах и в звездных атласах авторы ограничивались изображением лишь области, которую занимало созвездие. Обычно обозначалась самая яркая звезда - α Циркуля, но изображение самого циркуля не помещалось. Собственных имен звезды Циркуля не имеют.

Циркуль в снах.

Это хороший сон. Пользоваться циркулем во сне — значит, в скором времени вам предстоит дело, которое потребует от вас точного расчета. Чтобы усилить действие от этого сна, представьте, что вы чертите циркулем идеально ровные круги.

·         Увидеть во сне циркуль - признак того, что в скором времени Вам предстоит дело, которое потребует от Вас точного расчета.

·         Если Вам снится, что Вы циркулем чертите окружность, значит, что в ближайшее время Вас закружит водоворот дел.

·         Увидеть во сне сломанный циркуль означает, что ваше самолюбие будет оскорблено.

·         Уколоться циркулем означает, что нападки со стороны ваших коллег глубоко заденут Вас.

Циркуль в живописи

Тони Оррико - человек-циркуль. Удивительный американский художник использует свое тело, как инструмент, чтобы писать картины-абстракции.

В июле 2010 года в Миассе (город в составе Челябинской области в России (с 1926), основан город в 1773, входит в число исторических городов России.) открылся парк гигантской канцелярии. Организаторы установили на пьедесталы огромные ножницы, линейку, скрепку, циркуль и кнопку. Фигуры уже претендуют на то, чтобы попасть в Книгу рекордов Гиннеса. Например, циркуль весом 154 килограмма достигает в длину 6 метров. Возле каждого экспоната расположен стенд с информацией о мастере, а также об истории предмета – кто и когда его изобрел, какую роль он сыграл в истории прогресса. Все желающие смогут сфотографироваться на фоне гигантских «канцеляризмов». Миассцы ожидают, что их фигуры попадут в знаменитую книгу рекордов⁶. Оказывается, что циркуль имеет свой день – 9 августа День циркуля.

Таким образом, изучая значения изображений циркуля на различных предметах, можно сделать вывод, что оно является символом математики, умственного труда и правильного поведения.

VI. Применение циркуля в творческой деятельности

Я провел занятие со своими одноклассниками, на котором познакомил их со способами создания интересных узоров и рисунков с помощью циркуля. Вместе мы выполнили практические, творческие задания на построения.

Удивительный по красоте цветок рисуют при помощи циркуля, а затем заполняют цветом, если захочется.

VII. Способы решения стереометрических задач

В своей исследовательской работе хочу показать применение теоретических знаний и практических умений по черчению при решении геометрических задач. Такие задачи легко решить графическим способом, пользуясь циркулем и линейкой

Задача № 582 (Л.С. Атанасян Геометрия для 10-11 кл. 1994 г.)

Вершины прямоугольника лежат на сфере радиусом 10 см. Найти расстояние от центра сферы, до плоскости прямоугольника, если его диагональ равна 16 см.

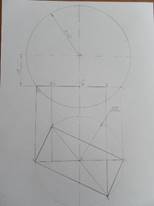
Этапы построения:

1.      Для удобства использую масштаб M 1:2

2.      На фронтально плоскости проекции(π2) строю фигуру по заданным размерам.

3.      Используя условия задачи (треугольник ABC вписан в окружность радиусом R=8 см.) находим место расположения прямоугольника ABCD.

4.      OO’ – на π2 является искомой величиной.

Ответ: OO’= 6 см.

Аналитический метод:

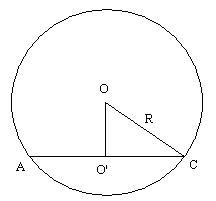
Дано:

АС=16 см

R=10 см

OO’-?

Решение:

1.      O’C=АС/2 т.к. ABCD- прямоугольник и 

2.      Проведем радиус сферы OC и получим прямоугольный ∆O’OC (т.к. OO’ _┴ пл. ABCD)

3.      По т. Пифагора

Ответ: 6 см.

Заключение

Итак, изучив журналы, публикации в Интернете и просто учебники, я познакомился с историей и различными аспектами применения, казалось бы, такого маленького, невзрачного предмета, как циркуль. Но какая у него история! Получилось что, занимаясь черчением и математикой, я изучил ряд вопросов из истории мировой культуры, вопросы из медицины, навигации, астрономии и даже производства. А, выполняя построения с помощью циркуля и линейки, я наблюдал красоту и эстетику геометрических фигур. При этом я узнал много новых интересных геометрических фактов о правильных многоугольниках и их углах. Я провел занятие со своими одноклассниками, на котором научил их создавать интересные узоры и рисунки с помощью циркуля. Я узнал, что в космосе есть созвездие Циркуля, неформальное общество масонов поклоняется этому предмету, его изображение присутствует на гербах и монетах. Таким образом, я могу сделать вывод: маленькое изобретение Талоса - циркуль, оказалось таким полезным, что нашло свое применение и в науке и в культуре. Циркуль до сих пор служит нам верой и правдой, помогая строить, измерять, производить продукцию, понимать и принимать культурное наследие человечества, и просто любоваться ...

Таким образом, моя гипотеза «что циркулем можно не только рисовать и создавать интересные узоры, но и решать геометрические задачи. Работа с циркулем - завораживающий процесс и не имеет никакого значения, умеете ли вы рисовать и фантазировать, удовольствие будет вам гарантировано» полностью подтвердилась.

А многими школьными «вещами» (транспортир, линейка) мы пользуемся постоянно но, к сожалению, мало о них знаем. Поэтому я предлагаю всем найти ещё что-нибудь интересное и необычное о различных школьных предметах. Возможно, вы тоже пополните свои знания интересными фактами, сделаете немало открытий и полюбите математику и черчение еще больше.

Список используемой литературы

1.      Анатасян Л.С. и др. Геометрия. Дополнительные главы к

школьному учебнику 9 класса, М., "Просвещение", 2007 г.

2.      Богданова Т.А., Лебедев Н.Н. Геометрические  построения 

ограниченными  средствами, Владимир, 1970 г.

3. Библиотека интересной научной литературы knigitut.net.

http://knigitut.net/1/3-1.htm

4. Детская энциклопедия "Я познаю мир" Математика, М., АСТ,1998 г.

5. Журнал «Советский музей», № 1, 1986 г.

6. Занимательное черчение

7. Интернет-журнал «Циркуль»,

http://cirkul.info/article/istoriya-tsirkulya.

8. Интернет-проект «Задачи»

http://www.problems.ru/view_by_subject_new.php?parent=834

9. «Кто изобрёл чертёжные принадлежности?»

http://lemill.net/commmunity/people/evelina0013.

10. Научно-методический журнал «Полином» № 3/2009 г.