Основні поняття теорії матричних ігор

Основні поняття теорії матричних ігор

Розглянемо гру, в якій беруть участь два гравці, причому кожний з гравців має кінцеве число стратегій. Позначимо для зручності одного з гравців через А, в іншого — через В.

Припустимо, що гравець А має  т стратегій — А₁, А₂, ... , А_т , а гравець В має  п стратегій В₁, В₂,...  , В.

Хай гравець А вибрав стратегію, а гравець В стратегію  .

Вважатимемо, що вибір гравцями стратегій   и     однозначно визначає результат гри – виграш    гравця А і виграш       гравця В, при цьому ці виграші зв'язані рівністю

(негативний виграш на побутовій мові зазвичай називають програшем).

Остання умова показує, що в розглянутих обставинах виграш одного з гравців рівний виграшу іншого, узятому з протилежним знаком. Тому при аналізі такої гри можна розглядати виграші тільки одного з гравців.

Хай це будуть, наприклад, виграші гравця А.

Якщо нам відомі значення    виграшу при кожній парі стратегій (у кожній ситуації) , i = 1, 2, ... , m;

                                      k = 1, 2,..., n,

то їх зручно записувати або у вигляді прямокутної таблиці, рядки якої відповідають стратегіям гравця А, а стовпці – стратегіям гравця В:

або у вигляді матриці:

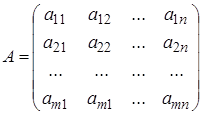
Отримана матриця має розмір т  п  і називається матрицею гри, або платіжною матрицею (звідси і назва гри – матрична).

Дану гру часто називають грою игрой m  n або m  n  игрой  грою.

Зауваження. Матричні ігри відносяться до розряду антагоністичних ігор, тобто ігор, в яких інтереси гравців прямо протилежні.