
Основна теорема теорії матричних ігор, властивості змішаних стратегій.
Теорема 1 (Дж. фон Нейман).
Для матричної гри з будь-якою матрицею А величини
![]()
рівні між собою,
![]()
Більше того, існує хоча б одна ситуація в змішаних стратегіях (Р, Q ), для якої виконується співвідношення
![]()
1) Іншими словами, будь-яка матрична гра має рішення в змішаних стратегіях. Пошук цього рішення опирається на наступні встановлені факти.
Основні властивості оптимальних змішаних стратегій.
Теорема 2. Нехай
![]()
– оптимальні змішані стратегії й v — ціна гри.
Оптимальна змішана стратегія Р° гравця А змішується тільки з тих чистих стратегій Аi , i = 1, 2,... , т, тобто відмінними від нуля можуть бути ймовірності рi тільки з тими номерами i = 1, 2,..., т, для яких виконані рівності
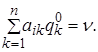
Це означає, що змішуються не всі чисті стратегії. Аналогічно,
в оптимальній змішаній стратегії Q° гравця У відмінні від нуля можуть бути тільки ті ймовірності qk, для номерів k = 1, 2, ..., п, для яких виконані рівності
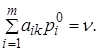
Крім того, мають місце співвідношення
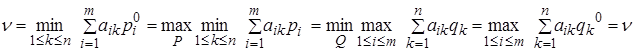
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.