
Индивидуальные работы повторения и подготовки к ЕГЭ для 10 класса
Работа 1 Повторение планиметрии
Вариант 1
1. Найдите периметр прямоугольника, если его площадь равна 272, а отношение соседних сторон равно 4 : 17.
2. 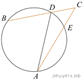 Найдите угол ACB, если вписанные углы ADB
и DAE опираются на дуги окружности, градусные величины которых равны
соответственно
Найдите угол ACB, если вписанные углы ADB
и DAE опираются на дуги окружности, градусные величины которых равны
соответственно ![]() и
и ![]() Ответ
дайте в градусах.
Ответ
дайте в градусах.
3. В треугольнике ABC угол A равен 60°, угол B равен 82°. AD, BE и CF — высоты, пересекающиеся в точке O. Найдите угол AOF. Ответ дайте в градусах.
4. Периметр треугольника равен 12, а радиус вписанной окружности равен 1. Найдите площадь этого треугольника.
5. В треугольнике ABC ![]() угол C
равен
угол C
равен ![]()
![]() Найдите
Найдите ![]()
6. 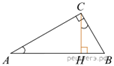 В треугольнике ABC угол C равен 90°, CH
− высота,
В треугольнике ABC угол C равен 90°, CH
− высота, ![]()
![]() Найдите
Найдите ![]()
7. Прямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного 4, отсекает треугольник, периметр которого равен 15. Найдите периметр трапеции.
8. Угол A четырехугольника ABCD, вписанного в окружность, равен 58°. Найдите угол C этого четырехугольника. Ответ дайте в градусах.
9.  Найдите хорду, на которую опирается угол 120°,
вписанный в окружность радиуса
Найдите хорду, на которую опирается угол 120°,
вписанный в окружность радиуса ![]()
10. В треугольнике ABC AB = BC. Внешний угол при вершине B равен 138°. Найдите угол C. Ответ дайте в гр
Вариант 2
1. Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 39?
2.  Диагонали четырехугольника равны 4 и 5. Найдите
периметр четырехугольника, вершинами которого являются середины сторон данного
четырехугольника.
Диагонали четырехугольника равны 4 и 5. Найдите
периметр четырехугольника, вершинами которого являются середины сторон данного
четырехугольника.
3.  Найдите вписанный угол, опирающийся на дугу, которая
составляет
Найдите вписанный угол, опирающийся на дугу, которая
составляет ![]() окружности. Ответ дайте в
градусах.
окружности. Ответ дайте в
градусах.
4. Найдите площадь треугольника, две стороны которого равны 34 и 8, а угол между ними равен 30°.
5. 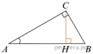 В треугольнике АВС угол С равен 90°,
В треугольнике АВС угол С равен 90°, ![]()
![]() Найдите
высоту СН.
Найдите
высоту СН.
6. Периметр треугольника равен 76, а радиус вписанной окружности равен 8. Найдите площадь этого треугольника.
7. 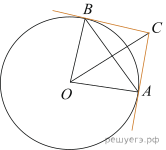 Касательные CA и CB к окружности образуют
угол ACB, равный 122°. Найдите величину меньшей дуги AB,
стягиваемой точками касания. Ответ дайте в градусах.
Касательные CA и CB к окружности образуют
угол ACB, равный 122°. Найдите величину меньшей дуги AB,
стягиваемой точками касания. Ответ дайте в градусах.
8. Основания трапеции равны 6 и 8. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей.
9. В треугольнике ABC AC = BC,
AB = 4, высота CH равна ![]() Найдите угол
Найдите угол ![]() Ответ
дайте в градусах.
Ответ
дайте в градусах.
10.  Четырехугольник ABCD вписан в окружность. Угол ABC
равен 110°, угол ABD равен 70°. Найдите угол CAD. Ответ дайте в
градусах.
Четырехугольник ABCD вписан в окружность. Угол ABC
равен 110°, угол ABD равен 70°. Найдите угол CAD. Ответ дайте в
градусах.
Вариант 3
1.  Найдите радиус окружности, вписанной в правильный
треугольник, высота которого равна 45.
Найдите радиус окружности, вписанной в правильный
треугольник, высота которого равна 45.
2. Сумма двух углов параллелограмма равна 82°. Найдите один из оставшихся углов. Ответ дайте в градусах.
3. 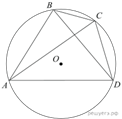 Четырехугольник ABCD вписан в окружность. Угол ABC
равен 98°, угол CAD равен 44°. Найдите угол ABD. Ответ дайте в
градусах.
Четырехугольник ABCD вписан в окружность. Угол ABC
равен 98°, угол CAD равен 44°. Найдите угол ABD. Ответ дайте в
градусах.
4. В треугольнике ABC угол A равен 40° , внешний угол при вершине B равен 102°. Найдите угол C. Ответ дайте в градусах.
5.  В окружности с центром O отрезки AC и BD —
диаметры. Центральный угол AOD равен 110°. Найдите вписанный угол ACB.
Ответ дайте в градусах.
В окружности с центром O отрезки AC и BD —
диаметры. Центральный угол AOD равен 110°. Найдите вписанный угол ACB.
Ответ дайте в градусах.
6. В треугольнике ABC угол C равен 90°, CH
− высота, ![]()
![]() Найдите
Найдите
![]()
7. 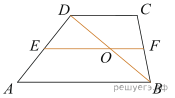 Основания трапеции равны 4 и 10. Найдите больший из
отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей.
Основания трапеции равны 4 и 10. Найдите больший из
отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей.
8. В треугольнике ABC AC = BC, AB = 10, высота AH равна 3. Найдите синус угла BAC.
9.  Хорда AB стягивает дугу окружности в 70°.
Найдите угол ABC между этой хордой и касательной к окружности,
проведенной через точку B. Ответ дайте в градусах.
Хорда AB стягивает дугу окружности в 70°.
Найдите угол ABC между этой хордой и касательной к окружности,
проведенной через точку B. Ответ дайте в градусах.
10.  Гипотенуза прямоугольного треугольника равна 28.
Найдите радиус описанной окружности этого треугольника.
Гипотенуза прямоугольного треугольника равна 28.
Найдите радиус описанной окружности этого треугольника.
Вариант4
1. В четырёхугольник ABCD вписана окружность, ![]() и
и ![]() Найдите периметр
четырёхугольника ABCD.
Найдите периметр
четырёхугольника ABCD.
2. 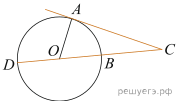 Угол ACO равен
Угол ACO равен ![]() Его
сторона CA касается окружности с центром в точке O. Сторона CO
пересекает окружность в точках B и D (см. рис.).
Найдите градусную меру дуги AD окружности, заключённой внутри этого
угла. Ответ дайте в градусах.
Его
сторона CA касается окружности с центром в точке O. Сторона CO
пересекает окружность в точках B и D (см. рис.).
Найдите градусную меру дуги AD окружности, заключённой внутри этого
угла. Ответ дайте в градусах.
3. В треугольнике ABC угол C равен 90°, ![]()
![]() Найдите
Найдите
![]()
4. Площадь ромба равна 6. Одна из его диагоналей в 3 раза больше другой. Найдите меньшую диагональ.
5. 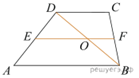 Основания трапеции равны 6 и 8. Найдите больший из
отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей.
Основания трапеции равны 6 и 8. Найдите больший из
отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей.
6. 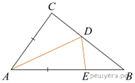 В треугольнике ABC угол B равен 45°, угол
C равен 52°, AD — биссектриса, E —
такая точка на AB, что AE = AC. Найдите
угол BDE. Ответ дайте в градусах.
В треугольнике ABC угол B равен 45°, угол
C равен 52°, AD — биссектриса, E —
такая точка на AB, что AE = AC. Найдите
угол BDE. Ответ дайте в градусах.
7. В треугольнике ABC ![]() Найдите
высоту
Найдите
высоту ![]()
8.  Четырехугольник ABCD вписан в окружность. Угол ABC
равен 105°, угол CAD равен 35°. Найдите угол ABD. Ответ дайте в
градусах.
Четырехугольник ABCD вписан в окружность. Угол ABC
равен 105°, угол CAD равен 35°. Найдите угол ABD. Ответ дайте в
градусах.
9. Центральный угол на 33° больше острого вписанного угла, опирающегося на ту же дугу окружности. Найдите вписанный угол. Ответ дайте в градусах.
10. 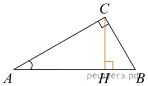 В треугольнике АВС угол С равен 90°,
В треугольнике АВС угол С равен 90°, ![]()
![]() Найдите
высоту СН.
Найдите
высоту СН.
Вариант5
1. В треугольнике ABC AC = BC,
AB = 9,6, ![]() Найдите AC.
Найдите AC.
2. 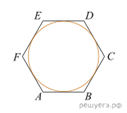 Найдите радиус окружности, вписанной в правильный
шестиугольник со стороной
Найдите радиус окружности, вписанной в правильный
шестиугольник со стороной ![]()
3. В треугольнике ABC угол C равен 90°,
высота CH равна 8, BC = 16. Найдите ![]()
4. Углы треугольника относятся как 1 : 1 : 10. Найдите меньший из них. Ответ дайте в градусах.
5. Найдите большую диагональ ромба, сторона которого
равна ![]() а острый угол равен
60°.
а острый угол равен
60°.
6. 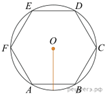 Чему равна сторона правильного шестиугольника,
вписанного в окружность, радиус которой равен 6?
Чему равна сторона правильного шестиугольника,
вписанного в окружность, радиус которой равен 6?
7. Основания равнобедренной трапеции равны 7 и 51. Тангенс
острого угла равен ![]() Найдите высоту
трапеции.
Найдите высоту
трапеции.
8.  Чему равен тупой вписанный угол, опирающийся на хорду,
равную радиусу окружности? Ответ дайте в градусах.
Чему равен тупой вписанный угол, опирающийся на хорду,
равную радиусу окружности? Ответ дайте в градусах.
9. 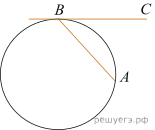 Хорда AB стягивает дугу окружности в 70°.
Найдите угол ABC между этой хордой и касательной к окружности,
проведенной через точку B. Ответ дайте в градусах.
Хорда AB стягивает дугу окружности в 70°.
Найдите угол ABC между этой хордой и касательной к окружности,
проведенной через точку B. Ответ дайте в градусах.
10. 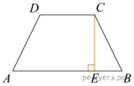 Основания равнобедренной трапеции равны 17 и 87. Высота
трапеции равна 14. Найдите тангенс острого угла.
Основания равнобедренной трапеции равны 17 и 87. Высота
трапеции равна 14. Найдите тангенс острого угла.
Вариант6
1. Сторона AB треугольника ABC равна 1. Противолежащий ей угол C равен 30°. Найдите радиус окружности, описанной около этого треугольника.
2.  Дуга окружности AC, не содержащая точки B,
составляет 210°. А дуга окружности BC, не содержащая точки A,
составляет 30°. Найдите вписанный угол ACB. Ответ дайте в градусах.
Дуга окружности AC, не содержащая точки B,
составляет 210°. А дуга окружности BC, не содержащая точки A,
составляет 30°. Найдите вписанный угол ACB. Ответ дайте в градусах.
3. В треугольнике ABC угол A равен ![]() угол B равен
угол B равен ![]() AD, BE и CF —
биссектрисы, пересекающиеся в точке O. Найдите угол AOF. Ответ
дайте в градусах.
AD, BE и CF —
биссектрисы, пересекающиеся в точке O. Найдите угол AOF. Ответ
дайте в градусах.
4. В четырёхугольник ABCD, периметр которого равен 54, вписана окружность, AB = 18. Найдите длину стороны CD.
5. Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 150°. Найдите боковую сторону треугольника, если его площадь равна 100.
6. Периметр параллелограмма равен 94. Одна сторона параллелограмма на 41 больше другой. Найдите меньшую сторону параллелограмма.
7. 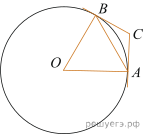 Через концы А и В дуги окружности с
центром О проведены касательные АС и ВС. Угол СAB
равен 32°. Найдите угол AОB. Ответ дайте в градусах.
Через концы А и В дуги окружности с
центром О проведены касательные АС и ВС. Угол СAB
равен 32°. Найдите угол AОB. Ответ дайте в градусах.
8. Найдите площадь прямоугольной трапеции, основания которой равны 1 и 7, большая боковая сторона составляет с основанием угол 45°.
9. 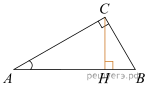 В треугольнике АВС угол С равен 90°,
В треугольнике АВС угол С равен 90°, ![]()
![]() Найдите СН.
Найдите СН.
10. 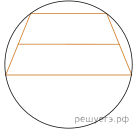 Около трапеции описана окружность. Периметр трапеции равен
38, средняя линия равна 11. Найдите боковую сторону трапеции.
Около трапеции описана окружность. Периметр трапеции равен
38, средняя линия равна 11. Найдите боковую сторону трапеции.
Ответы
|
вариант |
№1 |
№2 |
№3 |
№4 |
№5 |
№6 |
№7 |
№8 |
№9 |
№10 |
|
1 |
84 |
40 |
82 |
6 |
2 |
27 |
23 |
122 |
3 |
69 |
|
2 |
39 |
9 |
36 |
68 |
4,8 |
304 |
58 |
4 |
60 |
40 |
|
3 |
15 |
139 |
54 |
62 |
35 |
0,5 |
5 |
0,3 |
35 |
14 |
|
4 |
54 |
129 |
0,4 |
2 |
4 |
7 |
3 |
70 |
33 |
4,8 |
|
5 |
5 |
1,5 |
0,5 |
15 |
3 |
6 |
10 |
150 |
35 |
0,41 |
|
6 |
1 |
60 |
44 |
9 |
20 |
3 |
64 |
24 |
4 |
12 |
Работа 2 простейшие текстовые задачи
Вариант 1
1. Ежемесячная плата за телефон составляет 300 рублей в месяц. В следующем году она увеличится на 6%. Сколько рублей будет составлять ежемесячная плата за телефон в следующем году?
2. Налог на доходы составляет 13 % от заработной платы. После удержания налога на доходы Мария Константиновна получила 12 180 рублей. Сколько рублей составляет заработная плата Марии Константиновны?
3. При оплате услуг через платежный терминал взимается комиссия 5%. Терминал принимает суммы кратные 10 рублям. Аня хочет положить на счет своего мобильного телефона не меньше 300 рублей. Какую минимальную сумму она должна положить в приемное устройство данного терминала?
4. Цена на электрический чайник была повышена на 25 % и составила 2625 рублей. Сколько рублей стоил чайник до повышения цены?
5. В начале года число абонентов телефонной компании «Юг» составляло 600 тыс. человек, а в конце года их стало 630 тыс. человек. На сколько процентов увеличилось за год число абонентов этой компании?
6. Налог на доходы составляет 13% от заработной платы. Заработная плата Ивана Кузьмича равна 22 500 рублей. Какую сумму он получит после уплаты налогов? Ответ дайте в рублях.
7. Налог на доходы в России составляет 13% от заработной платы. Заработная плата Ивана Кузьмича равна 20 000 рублей. Сколько рублей он получит после уплаты налога на доходы?
8. Розничная цена учебника 180 рублей, она на 20% выше оптовой цены. Какое наибольшее число таких учебников можно купить по оптовой цене на 10 000 рублей?
9. Цена на электрический чайник была повышена на 20% и составила 2400 рублей. Сколько рублей стоил чайник до повышения цены?
10. В начале года число абонентов телефонной компании «Север» составляло 600 тыс. человек, а в конце года их стало 660 тыс. человек. На сколько процентов увеличилось за год число абонентов этой компании?
Вариант 2
1.Тетрадь стоит 10 рублей. Какое наибольшее число таких тетрадей можно будет купить на 650 рублей после понижения цены на 20%?
2. Ежемесячная плата за телефон составляет 300 рублей в месяц. В следующем году она увеличится на 6%. Сколько рублей будет составлять ежемесячная плата за телефон в следующем году?
3. Число посетителей сайта увеличилось за месяц впятеро. На сколько процентов увеличилось число посетителей сайта за этот месяц?
4. Тетрадь стоит 24 рубля. Сколько рублей заплатит покупатель за 60 тетрадей, если при покупке больше 50 тетрадей магазин делает скидку 10% от стоимости всей покупки?
5. Футболка стоила 800 рублей. После снижения цены она стала стоить 680 рублей. На сколько процентов была снижена цена на футболку?
6. В начале года число абонентов телефонной компании «Запад» составляло 700 тыс. человек, а в конце года их стало 840 тыс. человек. На сколько процентов увеличилось за год число абонентов этой компании?
7.Железнодорожный билет для взрослого стоит 290 рублей. Стоимость билета для школьника составляет 50% от стоимости билета для взрослого. Группа состоит из 16 школьников и 3 взрослых. Сколько рублей стоят билеты на всю группу?
8. В начале года число абонентов телефонной компании «Восток» составляло 800 тыс. человек, а в конце года их стало 880 тыс. человек. На сколько процентов увеличилось за год число абонентов этой компании?
9. Ивану Кузьмичу начислена заработная плата 20 000 рублей. Из этой суммы вычитается налог на доходы физических лиц в размере 13%. Сколько рублей он получит после уплаты подоходного налога?
10. Розничная цена учебника 180 рублей, она на 20% выше оптовой цены. Какое наибольшее число таких учебников можно купить по оптовой цене на 7900 рублей?
Вариант 3
1. Магазин закупает цветочные горшки по оптовой цене 120 рублей за штуку и продает с наценкой 20%. Какое наибольшее число таких горшков можно купить в этом магазине на 1000 рублей?
2. Только 94% из 27 500 выпускников города правильно решили задачу B1. Сколько человек правильно решили задачу В1?
3. В сентябре 1 кг огурцов стоил 50 рублей, в октябре огурцы подорожали на 20%, а в ноябре еще на 20%. Сколько рублей стоил 1 кг огурцов после подорожания в ноябре?
4. Цена на электрический чайник была повышена на 11 % и составила 2109 рублей. Сколько рублей стоил чайник до повышения цены?
5. Тетрадь стоит 10 рублей. Какое наибольшее число таких тетрадей можно будет купить на 650 рублей после понижения цены на 20%?
6. Среди 40 000 жителей города 60% не интересуется футболом. Среди футбольных болельщиков 80% смотрело по телевизору финал Лиги чемпионов. Сколько жителей города смотрело этот матч по телевизору?
7. Флакон шампуня стоит 170 рублей. Какое наибольшее число флаконов можно купить на 1100 рублей во время распродажи, когда скидка составляет 35%?
8. При оплате услуг через платежный терминал взимается комиссия 8%. Терминал принимает суммы, кратные 10 рублям. Аня хочет положить на счет своего мобильного телефона не меньше 500 рублей. Какую минимальную сумму она должна положить в приемное устройство данного терминала?
9. Клиент взял в банке кредит 12000 рублей на год под 13% годовых. Он должен погашать кредит, внося в банк ежемесячно одинаковую сумму денег, с тем чтобы через год выплатить всю сумму, взятую в кредит, вместе с процентами. Сколько рублей он должен вносить в банк ежемесячно?
10. Товар на распродаже уценили на 30%, при этом он стал стоить 350 рублей. Сколько рублей стоил товар до распродажи?
Вариант 4
1. Рост Джона 6 футов 1 дюйм. Выразите рост Джона в сантиметрах, если в 1 футе 12 дюймов, а в 1 дюйме 2,54 см. Результат округлите до целого числа сантиметров.
2. При оплате услуг через платежный терминал взимается комиссия 5%. Терминал принимает суммы кратные 10 рублям. Аня хочет положить на счет своего мобильного телефона не меньше 300 рублей. Какую минимальную сумму она должна положить в приемное устройство данного терминала?
3. Площадь земель фермерского хозяйства, отведённых под посадку сельскохозяйственных культур, составляет 63 га и распределена между зерновыми и бахчевыми культурами в отношении 4:5 соответственно. Сколько гектаров занимают бахчевые культуры?
4. Флакон шампуня стоит 160 рублей. Какое наибольшее число флаконов можно купить на 1000 рублей во время распродажи, когда скидка составляет 25% ?
5.В сентябре 1 кг огурцов стоил 50 рублей, в октябре огурцы подорожали на 20%, а в ноябре еще на 20%. Сколько рублей стоил 1 кг огурцов после подорожания в ноябре?
6. Число посетителей сайта увеличилось за месяц вчетверо. На сколько процентов увеличилось число посетителей сайта за этот месяц?
7.В городе N живет 1 500 000 жителей. Среди них 20% детей и подростков. Среди взрослых 35% не работает (пенсионеры, студенты, домохозяйки и т. п.). Сколько взрослых жителей работает?
8. 14 выпускников школы собираются учиться в технических вузах. Они составляют 28% от числа всех выпускников. Сколько в школе выпускников?
9. Налог на доходы составляет 13% от заработной платы. После удержания налога на доходы Мария Константиновна получила 13 050 рублей. Сколько рублей составляет заработная плата Марии Константиновны?
10. Ежемесячная плата за телефон составляет 240 рублей в месяц. В следующем года она увеличится на 5%. Сколько рублей будет составлять ежемесячная плата за телефон в следующем году?
Вариант 5 )
1. В городе N живет 500000 жителей. Среди них 20% детей и подростков. Среди взрослых 25% не работает (пенсионеры, студенты, домохозяйки и т.п.). Сколько взрослых жителей работает?
2. При оплате услуг через платежный терминал взимается комиссия 5%. Терминал принимает суммы кратные 10 рублям. Аня хочет положить на счет своего мобильного телефона не меньше 300 рублей. Какую минимальную сумму она должна положить в приемное устройство данного терминала?
3. Только 90% из 30000 выпускников города правильно решили задачу № 1. Сколько выпускников из этого города неправильно решили задачу № 1?
4. Ежемесячная плата за телефон составляет 250 рублей в месяц. В следующем году она увеличится на 4%. Сколько рублей будет составлять ежемесячная плата за телефон в следующем году?
5. Только 90% из 6000 выпускников города правильно решили задачу №2. Сколько выпускников из этого города правильно решили задачу №2?
6. Тетрадь стоит 7 рублей. Сколько рублей заплатит покупатель за 90 тетрадей, если при покупке больше 50 тетрадей магазин делает скидку 20% от стоимости всей покупки?
7. Тетрадь стоит 40 рублей. Какое наибольшее число таких тетрадей можно будет купить на 950 рублей после понижения цены на 25%?
8. Товар на распродаже уценили на 45%, при этом он стал стоить 110 рублей. Сколько рублей стоил товар до распродажи?
9. Налог на доходы составляет 13% от заработной платы. Заработная плата Ивана Кузьмича равна 22 500 рублей. Какую сумму он получит после уплаты налогов? Ответ дайте в рублях.
10. В начале года число абонентов телефонной компании «Юг» составляло 300 тыс. человек, а в конце года их стало 345 тыс. человек. На сколько процентов увеличилось за год число абонентов этой компании?
Вариант 6
1. В городе N живет 500000 жителей. Среди них 20% детей и подростков. Среди взрослых 25% не работает (пенсионеры, студенты, домохозяйки и т.п.). Сколько взрослых жителей работает?
2. Только 90% из 6000 выпускников города правильно решили задачу №2. Сколько выпускников из этого города правильно решили задачу №2?
3. В городе 180 000 жителей, причем 30% из них ― пенсионеры. Сколько жителей этого города не являются пенсионерами?
4. При оплате услуг через платежный терминал взимается комиссия 5%. Терминал принимает суммы кратные 10 рублям. Аня хочет положить на счет своего мобильного телефона не меньше 300 рублей. Какую минимальную сумму она должна положить в приемное устройство данного терминала?
5. Площадь земель фермерского хозяйства, отведённых под посадку сельскохозяйственных культур, составляет 42 га и распределена между зерновыми и техническими культурами в отношении 3 : 4. Сколько гектаров занимают технические культуры?
6. В магазине вся мебель продаётся в разобранном виде. Покупатель может заказать сборку мебели на дому, стоимость которой составляет 10 % от стоимости купленной мебели. Шкаф стоит 3100 рублей. Во сколько рублей обойдётся покупка этого шкафа вместе со сборкой?
7. Товар на распродаже уценили на 40%, при этом он стал стоить 810 рублей. Сколько рублей стоил товар до распродажи?
8. Налог на доходы составляет 13% от заработной платы. Заработная плата Ивана Кузьмича равна 31 500 рублей. Какую сумму он получит после уплаты налогов? Ответ дайте в рублях.
9. Футболка стоила 800 рублей. После снижения цены она стала стоить 680 рублей. На сколько процентов была снижена цена на футболку?
10. Городской бюджет составляет 82 млн рублей, а расходы на одну из его статей составили 15%. Сколько миллионов рублей потрачено на эту статью бюджета?
Ответы
|
вариант |
№1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
318 |
14000 |
320 |
2100 |
5 |
19575 |
17400 |
66 |
2000 |
10 |
|
2 |
81 |
318 |
400 |
1296 |
15 |
20 |
3190 |
10 |
17400 |
52 |
|
3 |
6 |
25850 |
72 |
1900 |
81 |
12800 |
9 |
550 |
1130 |
500 |
|
4 |
185 |
320 |
35 |
8 |
72 |
300 |
780000 |
50 |
15000 |
252 |
|
5 |
300000 |
320 |
3000 |
260 |
5400 |
504 |
31 |
200 |
19575 |
15 |
|
6 |
300000 |
5400 |
126000 |
320 |
24 |
3410 |
1350 |
27405 |
15 |
12,3 |
Работа 3 Формулы приведения
|
1 вариант 1) cos(π + x) 2) sin 3) tg(2π + x) 4) ctg 5) - sin 6) ¼ ctg(2π –x) 7) 8) 9)
|
2 вариант 1) cos(x – π) 2) sin 3) tg2(2π - x) 4) - ctg 5) 3cos(π + x) ) – cos(-2π – x) 6) tg(2π + x) 7) 8) 9) |
3 вариант 1) sin(π + x) 2) cos 3) ctg(2π+x) 4) tg 5) sin2(x – π) 6) tg 7) 8) 9)( |
|
4 вариант 1) sin 2) cos(π + x) 3) tg 4) tg3( 5) - cos 6) 5sin(-2π - x) 7) 8) sin 9) |
5 вариант 1) cos 2) sin(π–x)= 3) tg 4) ctg(2π - x) 5) cos 6) sin(π + x) 7) 8) 9)tg(-675) : cos(-570) – ctg 150 |
6 вариант 1) tg(2π - x) 2) ctg 3) cos(π–x)+ sin(-2π - x) 4) tg 5) ctg(π + x) 6) ctg(6π - x) 7) ctg315 8) 9)ctg |
Ответы
|
варианты |
№1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1 |
- |
cosa |
tga |
tga |
Cosa +2ctga |
-0,25ctga |
- |
|
|
|
2 |
cosa |
-cosa |
Tg2x |
tgx |
-2cosx |
-tgx |
|
1 |
|
|
3 |
-sinx |
-sinx |
ctgx |
ctgx |
Sin2x |
0 |
- |
|
-3 |
|
4 |
cosx |
-cosx |
-2ctgx |
Ctg3x |
-sinx |
-5sinx |
|
-
|
-0,5 |
|
5 |
sinx |
sinx |
Ctgx |
- ctgx |
-cosx |
-sinx |
1 |
- |
-1+ |
|
6 |
-tgx |
tgx |
-cosx-sinx |
-ctgx |
ctgx |
-ctgx |
-1 |
- |
|
Работа 5 Простейшие тригонометрические уравнения
|
1 вариант |
Вариант3 |
2 вариант |
|
1. sin 2. 2sin5x+1=0 3. 2cos 4. cos2x=1 5. sin 6. tg3x=1 7. 3ctg2x+ 8. 2sin4x+ 9. cos2x= - 10. tg 11. sin 12. cos 13. sin ( 14. cos ( 15. tg(0,5
|
1. sin 2. cos5x= - 3. tg2x=1 4. ctg 5. cos 6. sin ( 7. cos ( 8. tg ( 9. ctg ( 10. sin ( 11. cos 12. sin 2x= - 13. cos 14. 2sin5x- 15. 2cos
|
1. cos 2. 2sin2x-1=0 3. tg 4. 3ctg 5. sin ( 6. cos ( 7. tg ( 8. ctg ( 9. sin ( 10. cos 11. tg 12. ctg2x + 13. 2sin5x- 14. sin5x = - 1 15. tg (
|
|
5вариант |
Вариант6 |
4 вариант |
|
1. sin 2. cos2x= 3. tg 4. ctg 5. cos 6. sin ( 7. ctg ( 8. tg ( 9. 3sinx+1=0 10. 11. 3ctg2x - 12. 2cosx+1=0 13. sin4x=0 14. sin4x= – 15. |
1. sin 2. 2cos 3. 4. ctg 5. cos( 6. sin ( 7. tg ( 8. ctg ( 9. cos ( 10. sin 11. sin 12. tg 2x= 13. cos 2x=0 14. 2sin5x+ 15. ctg
|
1. sin 2. coos2x= - 3. tg 4. ctg2x = - 5. sin 6. sin ( 7. tg ( 8. ctg ( 9. sin ( 10. tg 11. 3ctg2x - 12. cos 13. sin 14. 15.
|
Работа 6 Тригонометрические уравнения
|
ВАРИАНТ 1 |
ВАРИАНТ 2 |
ВАРИАНТ 3 |
|
Решите тригонометрические уравнения: 1. 2sin2 x – 5sin x – 7 = 0 2. 12sin2 x + 20cos x – 19 = 0 3. 3sin2 x + 14sin x cos x + 8cos2 x = 0 4. 7 tg x – 10ctg x + 9 = 0 5. 5sin 2x – 14cos2 x + 2 = 0 6. 9cos 2x – 4cos2 x = 11sin 2x + 9
|
Решите тригонометрические уравнения: 1. 10cos2 x – 17cos x + 6 = 0 2. 2cos2 x + 5sin x + 5 = 0 3. 6sin2 x + 13sin x cos x + 2cos2 x = 0 4. 5 tg x – 4ctg x + 8 = 0 5. 6cos2 x + 13sin 2x = –10 6. 2sin2 x + 6sin 2x = 7(1 + cos 2x) |
Решите тригонометрические уравнения: 1. 3sin2 x – 7sin x + 4 = 0 2. 6sin2 x – 11cos x – 10 = 0 3. sin2 x + 5sin x cos x + 6cos2 x = 0 4. 4 tg x – 12ctg x + 13 = 0 5. 5 – 8cos2 x = sin 2x 6. 7sin 2x + 9cos 2x = –7 |
|
ВАРИАНТ 4 |
ВАРИАНТ 5 |
ВАРИАНТ 6 |
|
Решите тригонометрические уравнения: 1. 10cos2 x + 17cos x + 6 = 0 2. 3cos2 x + 10sin x – 10 = 0 3. 2sin2 x + 9sin x cos x + 10cos2 x = 0 4. 3 tg x – 12ctg x + 5 = 0 5. 10sin2 x – 3sin 2x = 8 6. 11sin 2x – 6cos2 x + 8cos 2x = 8 |
Решите тригонометрические уравнения: 1. 10sin2 x + 11sin x – 8 = 0 2. 4sin2 x – 11cos x – 11 = 0 3. 4sin2 x + 9sin x cos x + 2cos2 x = 0 4. 3 tg x – 8ctg x + 10 = 0 5. 3sin 2x + 8sin2 x = 7 6. 10sin2 x + 11sin 2x + 6cos 2x = –6
|
Решите тригонометрические уравнения: 1. 3cos2 x – 10cos x + 7 = 0 2. 6cos2 x + 7sin x – 1 = 0 3. 3sin2 x + 10sin x cos x + 3cos2 x = 0 4. 6 tg x – 14ctg x + 5 = 0 5. 6sin2 x + 7sin 2x + 4 = 0 6. 7 = 7sin 2x – 9cos 2x |
Ответы
|
вариант |
№1 |
2 |
3 |
4 |
5 |
6 |
|
1 |
– + 2pn {–1; 7/2} |
± + 2pn {1/2; 7/6} |
–arctg 4 + pn; –arctg + pk
|
–arctg 2 + pn; arctg + pk
|
+ pn; –arctg 6 + pk |
– + pn; –arctg + pk |
|
2 |
± + 2pn {1/2; 6/5} |
– + 2pn {–1; 7/2} |
–arctg 2 + pn; –arctg + pk
|
–arctg 2 + pn; arctg + pk
|
– + pn; –arctg + pk |
+ pn; –arctg 7 + pk |
|
3 |
+ 2pn {1; 4/3}
|
± + 2pn |
–arctg 3 + pn; –arctg 2 + pk
|
–arctg 4 + pn; arctg + pk
|
+ pn; –arctg + pk |
– + pn; arctg 8 + pk |
|
4 |
± + 2pn |
+ 2pn |
–arctg 2 + pn; –arctg + pk
|
–arctg 3 + pn; arctg + pk
|
– + pn; arctg 4 + pk |
+ pn; arctg + pk |
|
5 |
(–1)n × + pn |
p + 2pn |
–arctg 2 + pn; –arctg + pk
|
–arctg 4 + pn; arctg + pk
|
+ pn; –arctg 7 + pk |
– + pn; –arctg + pk |
|
6 |
2pn |
(–1)n + 1 × + pn |
–arctg 3 + pn; –arctg + pk
|
–arctg 2 + pn; arctg + pk
|
– + pn; –arctg + pk |
+ pn; –arctg 8 + pk |
Работа 7 Вычисление значений тригонометрических выражений
|
Вариант 1
2) 3) 4) 5) Найдите 6) Найдите значение выражения 7) Найдите значение выражения 8) Найдите значение выражения |
Вариант 2
2) 3) 4)
5) Найдите 6) Найдите значение выражения 7) Найдите значение выражения 8) Найдите значение выражения
|
Вариант 3 1.2 2. 3) 4) 5) Найдите 6) Найдите значение выражения 7) Найдите значение выражения 8) Найдите значение выражения
|
|
Вариант 4
2) 3) 4) 5) Найдите 6) Найдите значение выражения 7) Найдите значение выражения 8) Найдите значение выражения
|
Вариант 5
2) 3) 4) 5) Найдите 6) Найдите значение выражения 7) Найдите значение выражения 8) Найдите значение выражения
|
Вариант 6 1. ctg(2 2. 3) 4) 5) Найдите 6) Найдите значение выражения: 7) Найдите значение выражения 8) Найдите значение выражения
|
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.