План-конспект урока "Формулы объема пирамиды, конуса, цилиндра"

План-конспект урока №192-193

Индекс, наименование  дисциплины   ОДП.08 Математика

Преподаватель Василько Людмила Вениаминовна

Дата проведения______________________________

Группа_Э-25_

Тема программы Измерения в геометрии

Тема урока Формулы объема пирамиды, конуса, цилиндра.

Цели:

Обучающая: Знакомство с понятиями объем и его измерение, формулами объема куба, прямоугольного параллелепипеда, призмы, цилиндра.

Развивающая: Развивать пространственные представления и логическое мышление, организовать

деятельность обучающихся, направляя её на получение знаний

Воспитательная: Создать условия для формирования культуры учебной деятельности, умения        преодолевать трудности, вызова интереса к предмету

Тип урока:  изучение нового материала

  Вид урока:  лекция

Межпредметные связи:  физика, астрономия

Оснащение урока (материально-технические, дидактические средства, методические материалы): мультимедийный проектор, персональный компьютер, _конспект лекций

Литература: 1.Шарыгин И.Ф., Геометрия 10-11 класс, учебник, М.: Просвещение, 2021 год; 2. Башмаков М.И., Математика: учебник для НПО и СПО/ М.И. Башмаков. – 9-е изд., стер. – М.: Академия, 2018год; 3. Атанасян Л.С., Геометрия 10-11 класс, учебник, М.: Просвещение, 2014 год

Ход урока

1)   Организационный этап:

- Приветствие

- Доклад старосты об отсутствующих на уроке (причины)

- Объявление темы урока (На доске записана тема урока).

2) Постановка цели и задач урока. Мотивация учебной деятельности учащихся:

-Изложение целей урока.

-Проверка готовности обучающихся к уроку.

3) Актуализация знаний:

·                   Какое тело называют пирамидой, усеченной пирамидой?

·                         Какие тела вращения вам известны?

·                         Как можно получить цилиндр?

·                          Как можно получить конус?

·                          Как можно получить усечённый конус?

4) Изучение нового материала:

Площадь поверхности пирамиды

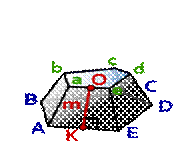S_бок = 1/2pm  p - периметр основания; m - апофема.

Площадь боковой поверхности правильной усеченной пирамиды

m - апофема пирамиды, отрезок OK

P - периметр нижнего основания, ABCDE

p - периметр верхнего основания, abcde

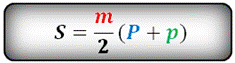 Формула площади боковой поверхности правильной усеченной пирамиды, (S):

 Апофемой называется высота боковой грани правильной пирамиды, проведенная из ее вершины

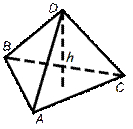Объем пирамиды

Объем пирамиды равен трети от произведения площади ее основания на высоту.

Формула объема пирамиды

где V- объем пирамиды, S_o- площадь основания пирамиды, h

- длина высоты пирамиды.

Расчёт объёма усечённой пирамиды

h - высота пирамиды

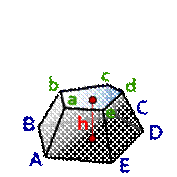S_ниж - площадь нижнего основания, ABCDE

S_верх - площадь верхнего основания, abcde

Объем усеченной пирамиды, (V):

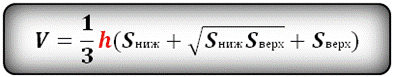
Площадь цилиндра

Площадь боковой поверхности круглого цилиндра равна произведению периметра его основания на высоту.

Формула для вычисления площади боковой поверхности цилиндра S = 2 π R h

Площадь полной поверхности круглого цилиндра равна сумме площади боковой 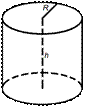поверхности цилиндра и удвоенной площади основания.

Формула для вычисления площади полной поверхности цилиндра

S = 2 π R h+ 2 π R ² = 2 π R( R+ h)

где S- площадь, R- радиус цилиндра, h- высота цилиндра, π = 3.141592

                             Объем цилиндра

Объем цилиндра равен произведению площади его основания на высоту.

Формулы объема цилиндра

V = π R² h   V = S_o h  где V- объем цилиндра, S_o- площадь основания цилиндра, R- радиус цилиндра, h- высота цилиндра,  π = 3.141592

 Площадь конуса

Площадь боковой поверхности конуса равна произведению его радиуса и образующей умноженному на число π

Формула площади боковой поверхности конуса: S = π R l

Площадь полной поверхности конуса равна сумме площади основания конуса и площади боковой поверхности.

Формула площади полной поверхности конуса: S =π R² + π R l= π R( R+ l)
где S- площадь, R- радиус основания конуса, l- образующая конуса, π = 3.141592

Формулы площади поверхности усеченного конуса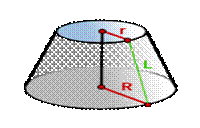

R - радиус нижнего основания

r- радиус верхнего основания

L - образующая усеченного конуса

π ≈ 3.14

Формула площади боковой поверхности усеченного конуса, (S_бок):

 Формула площади полной поверхности усеченного конуса, (S):

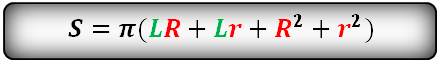
Объем конуса

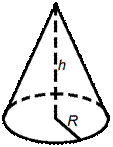Объем конуса равен трети от произведению площади его основания на высоту.

Формулы объема конуса

где V- объем конуса,

S_o- площадь основания конуса, R- радиус основания конуса, h- высота конуса, π = 3.141592

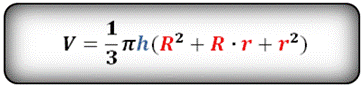
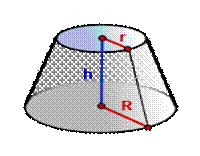Формула объема усеченного конуса

R- радиус нижнего основания

r- радиус верхнего основания

h- высота конуса

π ≈ 3,14

Объем усеченного конуса,  (V ):

5) Закрепление нового материала

1.Найдите объем цилиндрической мензурки с высотой, равной 3см и диаметром основания – 6см.

2. Найдите объем конуса, осевое сечение которого представляет собой равнобедренный прямоугольный треугольник с гипотенузой, равной 6√2  см.

3. Найти объем правильной треугольной пирамиды, высота которой равна 12 см, а сторона основания равна 13 см.

6) Информация о домашнем задании, инструктаж по его выполнению

 Выучить теорию и формулы объемов.

Решить задачу: Вода покрывает приблизительно ¾ земной поверхности. Сколько квадратных км занимает суша? (радиус земли считать равным 6375 км)

7) Рефлексия (подведение итогов занятия)

- выставление оценок

Преподаватель ___Василько Л.В.______________

Скачано с www.znanio.ru