
Публикация является частью публикации:
Методические рекомендации по суммативному оцениванию
Геометрия
7 класс
Методические рекомендации составлены в помощь учителю при планировании, организации и проведении суммативного оценивания за раздел по предмету «Геометрия» для обучающихся 7 классов. Методические рекомендации подготовлены на основе типовой учебной программы и учебного плана.
Задания для суммативного оценивания за раздел/тему позволят учителю определить уровень достижения учащимися целей обучения, запланированных на четверть. Для проведения суммативного оценивания за раздел/сквозную тему в методических рекомендациях предлагаются задания, критерии оценивания с дескрипторами и баллами. Также в сборнике описаны возможные уровни учебных достижений учащихся (рубрики). Задания с дескрипторами и баллами носят рекомендательный характер.
Методические рекомендации предназначены для учителей основной школы, администрации школ, методистов отделов образования, региональных и школьных координаторов по критериальному оцениванию и других заинтересованных лиц.
При подготовке методических
рекомендаций использованы ресурсы (рисунки, тексты, видео- и аудиоматериалы и
др.), находящиеся в открытом доступе на официальных интернет-сайтах.
ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 1 ЧЕТВЕРТЬ ................................... 4
Суммативное оценивание за раздел«Начальные геометрические сведения» .......................... 4
ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 2 ЧЕТВЕРТЬ ................................... 7
Суммативное оценивание за раздел «Треугольники» ................................................................ 7
ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 3 ЧЕТВЕРТЬ ................................. 10
Суммативное оценивание за раздел «Взаимное расположение прямых» .............................. 10
ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 4 ЧЕТВЕРТЬ ................................. 13
Суммативное
оценивание за раздел «Окружность. Геометрические построения» ............... 13
ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 1 ЧЕТВЕРТЬ
Тема Основные понятия геометрии. Аксиомы. Теоремы
Смежные и вертикальные углы, их свойства
Цель обучения 7.1.1.5 знать определения отрезка, луча, угла,
треугольника, полуплоскости
7.1.1.6 знать и применять аксиомы измерения отрезков и
углов
7.1.1.9 знать определения смежных и вертикальных
углов
Критерий оценивания Обучающийся
• Определяет по рисунку прямые, лучи, отрезки
• Использует аксиомы измерения углов для
решения задач
• Применяет аксиомы измерения отрезков для
решения задач
• Решает задачи, требующие применения свойств
вертикальных и смежных углов
Уровень мыслительных Знание и понимание
навыков Применение
Время выполнения 20 минут
Задания
1. Укажите названия следующих элементов на рисунке (прямая, луч, отрезок):
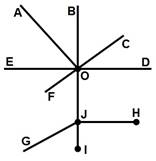 OA ______________
OA ______________
ED ______________
JH ______________
CF ______________
IB ______________
OJ ______________
JG ______________
2.
a) Начертите угол АОВ;
b) внутри угла проведите луч ОС;
c) найдите величину угла АОВ, если АОС12o, СОВ в 3 раза большеАОС.
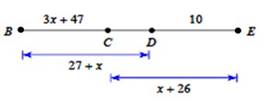
3. Найдите длину отрезка СЕ.
4.
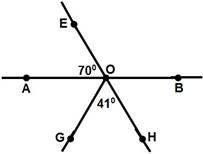 а) Запишите угол
смежныйHOB;
а) Запишите угол
смежныйHOB;
b) запишите две пары вертикальных углов;
c) вычислите величину HOB;
d) найдите величину AOG.
|
Критерий оценивания |
№ задания |
Дескриптор |
Балл |
|
Обучающийся |
|||
|
Определяет по рисунку прямые, лучи, отрезки |
1 |
записывает отрезки |
1 |
|
записывает лучи |
1 |
||
|
записывает прямые |
1 |
||
|
Использует аксиомы измерения углов для решения задач |
2 |
выполнен чертеж по условию задачи |
1 |
|
находит значение СОВ |
1 |
||
|
находит значение АОВ |
1 |
||
|
Применяет аксиомы измерения отрезков для решения задач |
3 |
составляет уравнение по условию задачи |
1 |
|
находит значение х |
1 |
||
|
находит отрезок CE |
1 |
||
|
Решает задачи, требующие применения свойств вертикальных и смежных углов |
4 |
записывает угол смежныйHOB |
1 |
|
записывает пары вертикальных углов |
1 |
||
|
находит величину HOB |
1 |
||
|
вычисляет величину AOG |
1 |
||
|
Всего баллов |
|
13 |
|
Рубрика для предоставления информации родителям по итогам суммативного оценивания за раздел
|
Критерий оценивания |
|
Уровень учебных достижений |
|
|
Низкий |
Средний |
Высокий |
|
|
Определяет по рисунку прямые, лучи, отрезки |
Затрудняется в определении прямых, отрезков и лучей по рисунку.
|
Допускает ошибки в определении прямых / отрезков / лучей по рисунку.
|
Верно определяет прямые, отрезки и лучи по рисунку.
|
|
Использует аксиомы измерения углов для решения задач |
Затрудняется в построении чертежа, применении аксиомы измерения углов.
|
Выполняет построение чертежа, допускает вычислительные ошибки при определении меры одного из углов.
|
Строит чертёж по условию задачи, верно находит значение углов, используя аксиомы измерения углов.
|
|
Применяет аксиомы измерения отрезков для решения задач |
Затрудняется в применении аксиомы измерения отрезков.
|
Допускает ошибки при нахождении значения
переменной / ошибки вычислительного характера при нахождении длины отрезка.
|
|
|
Решает задачи, требующие применения свойств вертикальных и смежных углов |
Затрудняется в применении свойств смежных и вертикальных углов.
|
Определяет смежные и вертикальные углы, допускает ошибки при нахождении величин углов.
|
Выполняет задания последовательно, определяет смежные и вертикальные углы, находит искомые углы.
|
6
ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 2 ЧЕТВЕРТЬ
|
Тема |
Медианы, биссектрисы, высоты и средние линии треугольника Признаки равенства треугольников Равнобедренный треугольник, его свойства и признаки |
|
Цель обучения |
7.1.1.12 знать определение медианы, биссектрисы, высоты, серединного перпендикуляра и средней линии треугольника и изображать их 7.1.1.21 знать и доказывать признаки равенства треугольников 7.1.1.22 применять признаки равенства треугольников при решении задач на вычисление и на доказательство 7.1.1.23 применять свойства и признаки равнобедренного треугольника |
|
Критерий оценивания |
Обучающийся • Определяет медиану, биссектрису, высоту треугольника по чертежу • Распознает равные элементы фигур и определяет соответствующий признак равенства треугольников • Использует свойства равнобедренного треугольника для решения задач • Применяет признаки равенства треугольников при решении задач на доказательство |
|
Уровень мыслительных навыков |
Применение Навыки высокого порядка |
|
Время выполнения Задания |
25 минут |
1. На рисунке изображен треугольник АВС. Укажите названия следующих элементов на рисунке (медиана, биссектриса, высота).
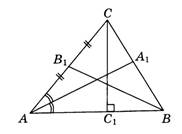 AA1 –
_____________________________
AA1 –
_____________________________
BB1 – _____________________________
CC1 – _____________________________
2. Луч AD – биссектриса угла ВАС. На сторонах угла отложены равные отрезки АВ и АС. Запишите равные элементы треугольников ВАD и САD и определите, по какому признаку треугольники равны.
7
3. В равнобедренном треугольнике АВС с основанием АС проведена медиана BD. Найдите градусные меры углов BDC и BCA, если и 1 1300 .
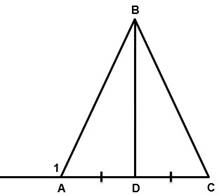
4. Треугольник DОВ – равнобедренный, ВD – основание, MDBKBD. Докажите, что DМ=ВК.
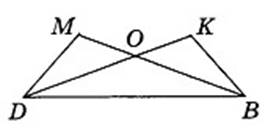
|
Критерий оценивания |
№ задания |
Дескриптор |
Балл |
|
Обучающийся |
|||
|
Определяет медиану, биссектрису, высоту треугольника по чертежу |
1 |
указывает медиану треугольника |
1 |
|
указывает биссектрису треугольника |
1 |
||
|
указывает высоту треугольника |
1 |
||
|
Распознает равные элементы фигур и определяет соответствующий признак равенства треугольников |
2 |
строит чертёж по условию задачи |
1 |
|
указывает равные элементы треугольников |
1 |
||
|
указывает соответствующий признак равенства треугольников |
1 |
||
|
Использует свойства равнобедренного треугольника для решения задач |
3 |
использует свойство медианы равнобедренного треугольника |
1 |
|
находит угол BDC |
1 |
||
|
находит угол BАC |
1 |
||
|
находит угол BCА |
1 |
||
|
Применяет признаки равенства треугольников при решении задач на доказательство |
4 |
использует равенство углов при основании равнобедренного треугольника |
1 |
|
доказывает равенство треугольников |
1 |
||
|
делает вывод о равенстве отрезков |
1 |
||
|
Всего баллов |
|
|
13 |
8
|
Критерий оценивания |
|
Уровень учебных достижений |
|
||
|
Низкий |
Средний |
Высокий |
|||
|
Определяет медиану, биссектрису, высоту треугольника по чертежу |
Затрудняется в определении медианы, биссектрисы, высоты треугольника.
|
Допускает ошибки при определении медианы / бисектрисы / высоты треугольника.
|
Верно определяет медиану, биссектрису, высоту треугольника по чертежу.
|
||
|
Распознает равные элементы фигур и определяет соответствующий признак равенства треугольников |
Затрудняется в определении равных элементов треугольников и соответствующего признака равенства тругольников.
|
Допускает ошибки в определении равных элементов треугольников или соотвтетствующего признака равенства треугольников.
|
Распознаёт равные элементы треугольников, верно определяет соответствующий признак равенства треугольников.
|
||
|
Использует свойства равнобедренного треугольника для решения задач |
Затрудняется в использовании свойств
равнобедренного треугольника. |
|
Использует свойства равнобедренного треугольника, верно находит все искомые углы. |
||
|
|
|
|
|||
|
Применяет признаки равенства треугольников при решении задач на доказательство |
Затрудняется в применении признаков равенства треугольников.
|
Доказывает равенство треугольников, но не делает вывод о равенстве отрезков.
|
Верно применяет признаки равенства треугольников при решении задач на доказательство.
|
||
9
ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 3 ЧЕТВЕРТЬ
|
Тема |
Параллельные прямые, их признаки и свойства Сумма углов треугольника. Внешний угол треугольника Признаки равенства прямоугольных треугольников. Свойства прямоугольного треугольника |
|
Цель обучения |
7.1.2.5 применять признаки параллельности прямых при решении задач 7.1.1.17 применять теорему о сумме внутренних углов треугольника и следствия из неё при решении задач 7.1.1.19 применять теорему о внешнем угле треугольника 7.1.1.27 применять свойства прямоугольного треугольника |
|
Критерий оценивания |
Обучающийся • Определяет параллельность прямых, используя признаки параллельности • Использует теоремы о сумме внутренних углов треугольника, о внешнем угле треугольника при решении задач • Применяет свойства прямоугольного треугольника при решении задач |
|
Уровень мыслительных навыков |
Применение Навыки высокого порядка |
|
Время выполнения |
25 минут |
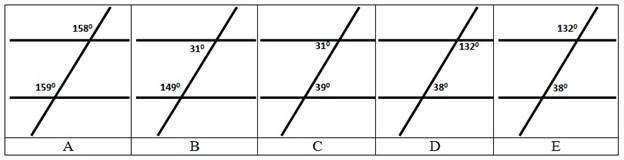
1. На каком из рисунков прямые будут параллельны? Поясните свой ответ.
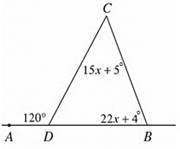
2. Используя теорему о внешнем угле треугольника, найдите угол С.
10
3. В треугольнике АВС A 600, C 800, CC1 – биссектриса треугольника АВС, CC1 6 см. Найдите длину отрезка ВC1.
4. В прямоугольном треугольнике АВС B 900, АВ = 8 см, АС = 16 см. Найдите углы, которые образует высота ВН с катетами треугольника.
|
Критерий оценивания |
№ задания |
Дескриптор |
Балл |
|
Обучающийся |
|||
|
Определяет параллельность прямых, используя признаки параллельности |
1 |
определяет параллельные прямые |
1 |
|
поясняет свой ответ, используя признаки параллельности |
1 |
||
|
Использует теоремы о сумме внутренних углов треугольника, о внешнем угле треугольника при решении задач |
2 |
использует теорему о внешнем угле треугольника |
1 |
|
находит значение х |
1 |
||
|
находит угол С |
1 |
||
|
3 |
использует теорему о сумме внутренних углов треугольника, находит углы треугольника ACC1 |
1 |
|
|
использует теорему о сумме внутренних углов треугольника, находит углы треугольника BCC1 |
1 |
||
|
находит длину отрезка ВC1 |
1 |
||
|
Применяет свойства прямоугольного треугольника при решении задач |
4 |
находит угол С |
1 |
|
находит угол СВН |
1 |
||
|
находит угол АВН |
1 |
||
|
Всего баллов |
|
|
11 |
11
Рубрика для предоставления информации родителям по итогам суммативного оценивания за раздел «Взаимное расположение прямых»
|
Критерий оценивания |
Уровень учебных достижений |
||
|
Низкий |
Средний |
Высокий |
|
|
Определяет параллельность прямых, используя признаки параллельности |
Затрудняется в выборе
признака параллельности прямых. |
Выбирает параллельные прямые, но не поясняет свой ответ.
|
|
|
Использует теоремы о сумме внутренних углов треугольника, о внешнем угле треугольника при решении задач |
Затрудняется в использовании теорем при решении задач.
|
Допускает ошибки вычислительного характера при использовании теоремы о сумме углов треугольника / теоремы о внешнем угле
треугольника. |
Верно использует теоремы о сумме внутренних углов треугольника, о внешнем угле треугольника, находит углы треугольника.
|
|
Применяет свойства прямоугольного треугольника при решении задач |
Затрудняется в использовании свойства катета, против угла в 30 градусов, что затрудняет решение задачи в целом.
|
Использует свойство катета
в прямоугольном треугольнике, равного половине гипотенузы, но не находит
углы, которые образует высота с катетами треугольника. |
Использует свойство катета в прямоугольном
треугольнике, равного половине гипотенузы, верно находит углы, которые
образует высота с катетами треугольника. |
12
ЗАДАНИЯ ПО СУММАТИВНОМУ ОЦЕНИВАНИЮ ЗА 4 ЧЕТВЕРТЬ
|
Тема |
Окружность, круг, их элементы и части. Центральный угол Касательная к окружности. Свойства касательных к окружности Задачи на построение |
|
Цель обучения |
7.1.2.13 знать и применять свойства касательной к окружности при решении задач 7.1.1.30 доказывать и применять теоремы о перпендикулярности диаметра и хорды 7.1.2.18 строить треугольник по заданным элементам 7.1.2.17 строить серединный перпендикуляр к отрезку, прямую, перпендикулярную к данной прямой |
|
Критерий оценивания |
Обучающийся • Применяет свойства касательной при решении задач • Применяет теоремы о перпендикулярности диаметра и хорды при решении задач • Выполняет построение треугольника, серединного перпендикуляра к отрезку |
|
Уровень мыслительных навыков |
Применение Навыки высокого порядка |
|
Время выполнения Задание |
25 минут |
1. Две прямые касаются окружности с центром О в точках А и В и пересекаются в точке С. Найдите угол между этими прямыми, если ABO400 .
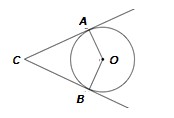
2. Из центра окружности О к хорде АВ, равной 20 см, проведен перпендикуляр ОС.
Найдите длину перпендикуляра, если ОАВ45o.
3. a) Постройте треугольник АВС по трем сторонам.
b) Постройте серединный перпендикуляр к стороне АВ.
13
|
Критерий оценивания |
№ задания |
Дескриптор |
Балл |
|
Обучающийся |
|||
|
Применяет свойства касательной при решении задач |
1 |
строит чертёж по условию задачи |
1 |
|
определяет вид треугольника АОВ |
1 |
||
|
использует свойство касательной ( радиусу) и определяет углы АВС и ВАС |
1 |
||
|
находит величину искомого угла |
1 |
||
|
Применяет теоремы о перпендикулярности диаметра и хорды при решении задач |
2 |
применяет теорему о перпендикулярности диаметра и хорды и находит длину АС |
1 |
|
определяет вид треугольника |
1 |
||
|
находит длину перпендикуляра |
1 |
||
|
Выполняет построение треугольника, серединного перпендикуляра к отрезку |
3 |
использует неравенство треугольника для определения существования треугольника |
1 |
|
выполняет построение отрезка, равного данному |
1 |
||
|
выполняет построение треугольника по трем сторонам |
1 |
||
|
выполняет построение серединного перпендикуляра |
1 |
||
|
Всего баллов |
|
|
11 |
14
Рубрика для предоставления информации родителям по итогам суммативного оценивания за раздел «Окружность. Геометрические построения»
|
Критерий оценивания |
Уровень учебных достижений |
|
|
|
Низкий |
Средний |
Высокий |
|
|
Применяет свойство касательной при решении задачи |
Затрудняется в использовании свойств касательной.
|
Использует
перпендикулярность касательной и радиуса, допускает ошибки при нахождении
искомого угла. |
Использует свойство касательной, находит величину искомого угла.
|
|
Применяет теоремы о перпендикулярности диаметра и хорды при решении задач |
Затрудняется в использовании теоремы.
|
Использует теорему о перпендикулярности диаметра и хорды, допускает ошибки в обосновании вида треугольника / нахождении искомого отрезка.
|
Использует теорему о перпендикулярности
диаметра и хорды, использует свойство равнобедренного прямоугольного
треугольника, находит искомый отрезок. |
|
Выполняет построение треугольника, серединного перпендикуляра к отрезку |
Затрудняется в построении треугольника, серединного перпендикуляра к отрезку.
|
Допускает погрешности в построении треугольника / серединного перпендикуляра к отрезку.
|
Выполняет построение треугольника по трем
сторонам, делает вывод о существовании треугольника. Выполняет построение
серединного перпендикуляра к отрезку. |
15
Сдано в набор 29.07.2017. Подписано в печать 31.07.2017. Формат 60х84/8. Бумага офисная 80 гр/м2. Печать цифровая. Усл. печ. л.1,68. Тираж 19 экз. Заказ № 1574 Отпечатано в типографии ЧУ «Центр педагогического мастерства» 010000. г. Астана, ул. №31, дом 37а. e-mail: info@cpm.kz
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.