Добавить материал

и получить 10 документов
и свидетельство СМИ

Шкода Лидия Ильинична

Подготовки к ГВЭ и ЕГЭ. Окружность. 11 класс.

Рабочие листы
docx
06.04.2021

Публикация в СМИ для учителей

Бесплатное участие. Свидетельство СМИ сразу.
Мгновенные 10 документов в портфолио.

Добавить материал

Работа содержит 3 типа разобранных задач на вписанные, центральные углы и на вычисление площади круга. Даны по 4 задачи на каждый тип для самостоятельного решения. В конце работы даны ответы на задачи.

Повт.Подг.к ГВЭ.Окружностбь.docx

Повторение. Окружность.

Рассмотрим решения задач и решим самостоятельно.

Задача 1. Найдите вписанный угол, опирающийся на дугу, которая составляет окружности. Ответ дайте в градусах.

Решение.

Вписанный угол равен половине дуги, на которую опирается. Следовательно

$\angle ACB= дробь, числитель — 1, знаменатель — 2 \cup AB= дробь, числитель — 1, знаменатель — 2 умножить на дробь, числитель — 1, знаменатель — 5 умножить на 360{} в степени circ =36{} в степени circ .$

Ответ: 36.

Самостоятельно.

1. Найдите вписанный угол, опирающийся на дугу, которая составляет 40 % окружности. Ответ дайте в градусах.

2. В окружности с центром и – диаметры. Центральный угол равен . Найдите вписанный угол . Ответ дайте в градусах.

3. Четырехугольник вписан в окружность. Угол равен , угол равен . Найдите угол . Ответ дайте в градусах.

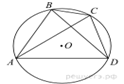
4. В окружности с центром и — диаметры. Центральный угол равен $130 в степени \circ$ . Найдите вписанный угол . Ответ дайте в градусах.

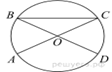
Задача 2 . Вписанный угол окружности на 42° меньше центрального угла, опирающегося на ту же дугу данной окружности. Найдите вписанный угол. Ответ дайте в градусах.

Решение.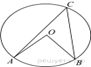

Введём обозначения, как показано на рисунке. Вписанный угол равен половине центрального угла, опирающегося на ту же дугу окружности, значит

$\angle ACB плюс 42{} в степени circ =2\angle ACB равносильно \angle ACB=42{} в степени circ .$

Ответ: 42.

Самостоятельно.

5. В окружности с центром O проведён диаметр AB и на окружности взята точка C так, что угол COB равен 120°, AC = 50. Найдите диаметр окружности.

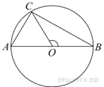
6. На окружности с центром отмечены точки и так, что $\angleАОВ=2 в степени circ$ . Длина меньшей дуги равна 46. Найдите длину большей дуги.

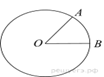
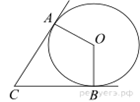
7. В угол C, равный 68°, вписана окружность с центром O, которая касается сторон угла в точках A и B. Найдите угол AOB. Ответ дайте в градусах.

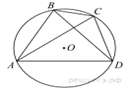
8. Четырехугольник вписан в окружность. Угол равен , угол равен . Найдите угол . Ответ дайте в градусах.

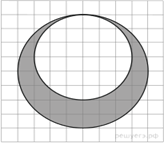
Задача 3 . На клетчатой бумаге нарисовано два круга. Площадь внутреннего круга равна 9. Найдите площадь заштрихованной фигуры.

Решение.

Площади кругов относятся как квадраты их радиусов. Поскольку радиус большего круга равен четырем третьим радиуса меньшего круга, площадь большего круга составляет шестнадцать девятых площади меньшего. Следовательно, она равна 16. Площадь заштрихованной фигуры равна разности площадей кругов: 16 − 9 = 7.

Ответ: 7.

Самостоятельно.

9. На клетчатой бумаге нарисовано два круга. Площадь внутреннего круга равна 1. Найдите площадь заштрихованной фигуры.

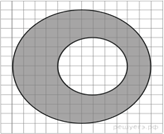
10. Найдите (в см²) площадь кольца, изображенного на клетчатой бумаге с размером клетки 1 см $\times$ 1 см (см. рис.). В ответе запишите .

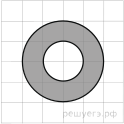
11. На клетчатой бумаге нарисованы два круга. Площадь внутреннего круга равна 51. Найдите площадь заштрихованной фигуры.

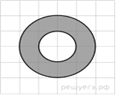
12. Вычислите площадь кругового сектора, радиус которого равен 6 см, угол α сектора равен 135°. Результат разделите на.

(Примечание. Площадь кругового сектора вычисляется по формуле: S= ).

Ответы на задачи.

№ 1	72
№ 2	35
№ 3	70
№ 4	25
№ 5	100
№ 6	8234
№ 7	112
№ 8	40
№ 9	3
№ 10	3
№ 11	153
№ 12	13,5

Повторение. Окружность. Рассмотрим решения задач и решим самостоятельно

Решение. Введём обозначения, как показано на рисунке

Решение. Площади кругов относятся как квадраты их радиусов

Ответы на задачи. № 1 72 № 2 35 № 3 70 № 4 25 № 5 100 № 6 8234 № 7 112 №…

Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

Посмотрите также