ПР 1 ТЕПЕРІШНЯ ВАРТІСТЬ ЦІННИХ ПАПЕРІВ

 ПР 1 ТЕПЕРІШНЯ ВАРТІСТЬ  ЦІННИХ ПАПЕРІВ

1.1            Мета роботи

Метою заняття є вивчення математичної бази для обчислювання грошових сум, нарощених за початковим вкладом. Вона є основою для більш складних розрахунків, наприклад, потоків платежів або інвестицій.

1.2             Методичні вказівки з організації самостійної роботи студентів

2                   Для вивчення теми під час підготовки до практичних занять студенту необхідно скористатися  [1, с. 4-28], [2, с. 7-41].

3                   У навчальному посібнику [1] наводяться методи комерційних розрахунків, а також основи портфельної теорії: ефективної траєкторії; лінії ринків цінних паперів і капіталу. Розглядаються питання обліку імовірнісної та діапазонної невизначеностей: ризики, їхні вимірники, відносини до ризику і функції корисності. Численні приклади, що роз’ясняють, рисунки і графічні ілюстрації полегшують сприйняття теоретичного матеріалу і роблять його доступним для самостійного освоєння . Для підготовки до самостійної роботи корисними будуть теоретичні питання щодо розрахунку поточної вартості облігацій.

4                   У навчальному посібнику [2] розглядаються питання визначення нарощених і дисконтованих сум, потоків платежів, ренти, дюрації. Наведені задачі для самостійного розв¢язання.

5                   Під час підготовки до практичного заняття  слід вивчити питання фінансового ринку і ризику; встановити, хто є учасником фінансового ринку та їхні відносини до ризику. Крім того, слід приділити увагу таким питанням, як види цінних паперів; облігації як мало ризикові цінні папери; розрахунок поточної вартості облігацій.

Для досягнення поставленої мети практичного заняття студент повинен ознайомитися з рекомендованою до вивчення літературою, теоретичними відомостями даних методичних вказівок, розглянути приклади розв¢язання задач за темою а також розв‘язати задачі, що запропонував викладач. За відсутності достатньої кількості примірників  навчальної літератури з дисципліни в бібліотеці університету, слід надати основну теоретичну інформацію  в даних методичних вказівках.

Для  стислого описання теоретичних зведень по темі практичного заняття варто поділити теоретичний матеріал на кілька підтем:

–             нарощення простих відсотків;

–             нарощення складних відсотків;

–             потоки платежів, рента;

Прості та складні відсотки

При нарощенні простих відсотків формула розрахунку майбутніх сум  за початковим внеском  по ставці  до кінця одиничного періоду має такий вигляд:

 ,                                              (1.1)

тобто на , до кінця -го проміжку обчислення ця сума стане – кожна подальша сума більше попередньої на частку  від початкової суми .

Нарощена таким чином послідовність сум  є арифметичною прогресією з початковим членом  і різницею .

Сума , нарощена по ставці  простих відсотків, через  проміжків нарахування буде .

 При нарощенні складних відсотків по ставці  кожна подальша сума зросте на частку  від попередньої. Отже, до кінця одиничного проміжку нарахування сума  зросте на частку  і стане , до кінця другого – ця сума зросте ще на частку  від , і буде . До кінця -го проміжку – . Отже, послідовність нарощених сум  є геометричною прогресією з початковим членом  і знаменником прогресії . Сума , нарощена по ставці  складних відсотків, через  проміжків нарахування буде .

6                   Перерахування майбутньої суми до дійсного моменту називається дисконтуванням  її величини.

Для простого нарощення відсотків коефіцієнт дисконтування  дорівнює ,  а для  складного – .

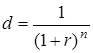Нарахування за схемою простих відсотків застосовується, як правило, в короткострокових фінансових операціях, коли інтервал нарахування співпадає з періодом нарахування (і дорівнює строку менше одного року), або коли після кожного інтервалу нарахування кредитору виплачуються відсотки. Природно, що нарахування простих відсотків може застосовуватись і в будь-яких інших випадках за домовленістю сторін, що беруть участь в операції.

Якщо простий відсоток нараховується протягом періоду, який складає менше року, формула (1.1) набуває вигляду:

                                                                              (1.2)

де: t – кількість днів нарахування відсотку протягом року;

Т – кількість днів в році;

Pt – сума, яка одержується при нарахуванні відсотку за t днів;

r – відсоток, що нараховується.

Якщо не зазначено інше, звичайно нарахований відсоток задається як відсоток в розрахунку на рік. Тоді за t днів буде нарахована тільки його частина, а ааме  або .

                                                          (1.3)

або

,                                                        (1.4)

В формулі (1.3) фінансовий рік складатиме 360, а в формулі (1.4) – 365 днів. Вибір формули (1.3) або (1.4) залежить від того, з яким інструментом працює інвестор. Так, в банківській системі рік вважається рівним 360 дням. Тому розрахунки по нарахуванню відсотків по вкладах потрібно робити за допомогою формули (1.3). Розрахунки по операціях з державними короткостроковими облігаціями здійснюються на базі, рівній 365 дням. В цьому випадку використовують формулу (1.3).

У довгострокових фінансово-кредитних угодах частіше використовують нарахування складних відсотків. При нарахуванні складних відсотків їх нараховують не тільки на основну суму, а й на суму, що включає як основну суму, так і нараховані раніше відсотки. У цьому випадку кажуть, що відбувається капіталізація відсотків в міру їх нарахування.

Відповідно до ідеології нарахування складних відсотків за перший період нарахування відсотків базою для нарахування є основна сума:

Р1 = Р (1 + r)

Відмінність результатів для складного і простого відсотків виникає, починаючи з другого періоду нарахування, оскільки в кінці другого року його капітал зросте до:

Р2 = Р (1 + r) + Р(1 + r) r = Р (1 + r) (1 + r) = Р (1 + r)²

В кінці третього року він складе:

Р3 = Р (1 + r)² + Р(1 + r)² r = Р (1 + r)² (1 + r) = Р (1 + r)³

Аналогічно можна показати, що через n років сума на рахунку зросте до величини:

Рn = Р (1 + r)ⁿ                                                                     (1.5)

Формула складних відсотків є однією з базових формул у фінансових розрахунках, тому для зручності користування значення множника , який носить назву мультиплікованого множника і який забезпечує нарощення вартості, табульовані для різних значень r і n (див. Додаток 1).

Приклад

250000 грн. інвестовані на 4 роки під 6 % річних. Яку суму одержить інвестор в кінці строку?

Нарахування відсотків декілька разів на рік.

Складний відсоток може нараховуватися частіше, ніж один раз на рік, наприклад, раз в півроку, квартал, місяць тощо. Нарахування складних відсотків декілька разів на рік називається компаундингом. Як правило, у фінансових контрактах фіксується річна відсоткова ставка і при цьому відсотки можуть нараховуватися по півріччях, кварталах, місяцях тощо. Відсотки, що нараховуються з певною періодичністю, називаються дискретними. В цьому випадку річна ставка називається номінальною, а відсоткова ставка за один інтервал нарахування вважається рівною відношенню номінальної ставки до кількості інтервалів в році. Нарощена сума буде розраховуватись за наступною формулою:

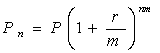,                                        (1.6)

де: m – періодичність нарахування відсотку протягом року.

Приклад

На вклад до банку в розмірі 9000 грн. строком на 5 років банк нараховує 18 % річних. Яка сума буде на рахунку в кінці строку, якщо нарахування відсотків здійснюється за схемою складних відсотків: а) щопівроку; б) щоквартально?

А)

б)

Комбінація простого і складного відсотків. Досить часто фінансові контракти укладаються на період, що відрізняється від цілої кількості років. В цьому випадку відсотки можуть нараховуватись або за схемою складних відсотків (формула (1.5)), або за схемою, яка передбачає нарахування відсотків, що включає і складний, і простий відсотки (за змішаною схемою).

Наприклад, кошти вкладника знаходяться на рахунку в банку n років і t днів. Відсотки капіталізуються (тобто приєднуються до основної суми коштів, на яку нараховується відсоток) в кінці кожного року. Протягом року нараховується простий відсоток. Для такого випадку суму, яку одержить інвестор, можна розрахувати за наступною формулою:

,                             (1.7)

де: Pn+t – сума, яку одержить інвестор за n років і t днів;

P – початково інвестована сума;

t – число днів, за які нараховується простий відсоток;

r – відсоток, що нараховується протягом року.

На практиці в цьому випадку часто користуються формулою складних відсотків з відповідними нецілими показниками ступеня. Але потрібно взяти до уваги, що з точки зору сутності нарахування відсотків цей спосіб є приблизним і погрішність при розрахунках буде тим більшою, чим більше значення величин, що входять до формули. Потрібно враховувати, що приблизний метод дає менший, ніж є в дійсності, результат.

Приклад

Нехай 6000 грн. інвестовані на 1 рік і 4 місяці під складні відсотки за ставкою 22 % річних. Знайти нарощену до кінця строку суму а) за схемою складних відсотків; б) за змішаною схемою.

А)

б)

В залежності від того, коли вкладник розміщує кошти на рахунку, простий відсоток може нараховуватись також на початку періоду інвестування коштів або і на початку, і в кінці. Суми, які одержить вкладник, можна розрахувати за допомогою формул (1.8) і (1.9) (капіталізація відсотків здійснюється щорічно):

,                                   (1.8)

,                         (1.9)

Еквівалентний і ефективний відсотки. В практиці фінансового ринку відсоток, що нараховується по активу, задають як простий відсоток з розрахунку на рік. Однак, якщо в рамках року по активу передбачено нарахування складного відсотку, то загальний результат, який одержить інвестор, буде вище декларованого. Щоб його визначити, необхідно розрахувати ефективний або реальний відсоток.

Ефективний (реальний) відсоток – це відсоток, який одержується за результатами року при нарахуванні складного відсотку.

Ефективний відсоток можна визначити з наступного співвідношення:

,                                                     (1.10)

де: rеф – ефективний відсоток;

r – простий відсоток з розрахунку на рік, який заданий за умовами фінансового інструменту.

                                                       (1.11)

Приклад

Знайти річну ефективну відсоткову ставку, еквівалентну номінальній ставці 16 % при щоквартальному нарахуванні відсотків.

 або 16,99 %

Якщо відомий ефективний відсоток, то можна визначити еквівалентний йому простий відсоток з розрахунку на рік:

                                                     (1.12)

Приклад

, нарахування проводяться раз у півроку. Визначити еквівалентний простий відсоток.

або 14,48 %