Практическая работа по теме "Золотое сечение".

Практическая работа «Золотое сечение в природе»

Цель: Найти примеры  «золотого сечения»  в природе,  в жизни людей.

Общие сведения:

          "Божественная гармония" или золотое сечение – правило соотношения частей и целого, универсальное проявление красоты и симметрии. Оно встречается в науке, природе, архитектуре, искусстве.

         "Первым про золотое сечение писал еще Евклид в “Началах”, которые в свое время были вторые по популярности после Библии. 

 Золотое сечение – это такое  пропорциональное деление отрезка на неравные части, при котором  весь отрезок так относится  к большей части, как сама  большая часть относиться к меньшей.

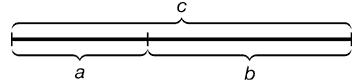 a:b  =b:c =0,618;       где   c  =  a+ b

Или    b: a =c : b =1,618

"Если взять для примера линию и разделить ее на две части так, чтобы длинная соотносилась с короткой в такой же пропорции, как вся линия соотносится с длинной, получится золотая пропорция",

К слову, она равна всегда 1,618, и это так называемое число "фи" обозначается греческой буквой φ — от имени древнегреческого скульптора Фидия.

Пропорции золотого сечения

"Если взять для примера линию и разделить ее на две части так, чтобы длинная соотносилась с короткой в такой же пропорции, как вся линия соотносится с длинной, получится золотая пропорция",   К слову, она равна всегда 1,618, и это так называемое число "фи" обозначается греческой буквой φ — от имени древнегреческого скульптора Фидия.  В правильном прямоугольнике соотношение сторон соответствует золотому сечению.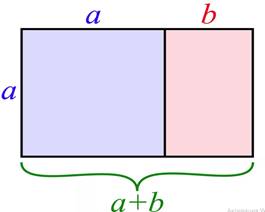

"Интересен этот прямоугольник тем, что сколько бы ни отрезали от него квадратов, он всегда будет оставлять после себя кусочек с золотым соотношением сторон и так до бесконечности",

Золотое сечение в математике

Итальянский астроном и математик Фибоначчи вывел ряд чисел, в котором значение каждого последующего равно сумме двух предыдущих. Эта закономерность известна как ряд Фибоначчи.

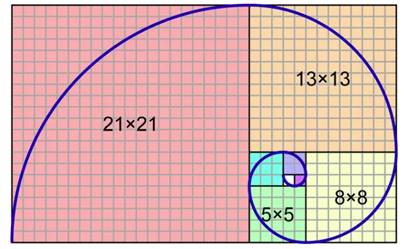
"Если представить два квадрата, поставленных рядом, потом добавить квадрат с удвоенной стороной, то получится квадрат 2 на 2. Далее добавить по спирали против часовой стрелки сумму двух предыдущих квадратов. Получится квадрат с длинной стороны три квадрата, далее добавить к стороне квадрата предыдущую сторону, получится 5, потом 8 потом 13 и 21, каждое последующее число - это сумма сложения с предыдущим, то есть получается такая последовательность, которую и вывел Фибоначчи: 0,1,1,2,3,5,8,13,21 и т.д.", 

0, 1,1 (0+1), 2 (1+1), 3 (1+2), 5 (2+3), 8 (3+5), 13 (5+8), 21 (8+13), 34 (13+21), 55 (21+34), 89 (34+55) и до бесконечности. А при делении последующего числа на предыдущее получается коэффициент золотого сечения. По мере возрастания чисел соотношение приближается к 1,618. К примеру, числа 3 и 5, их соотношение равно 1,666, а если взять 13 и 21, то получается уже 1,625. Данную формулу применяют для расчета пропорций золотого сечения в любой отрасли, на практике чаще всего используют округленное значение 0,62.

А если в каждом квадрате построить дугу из одного угла к другому, то получится так называемая спираль Фибоначчи.

Человек

Пропорции золотого сечения прослеживаются и на примере тела человека. К золотой формуле приравнивается абсолютно все: кости, ладони и пальцы, пропорции участков на лице, расстояние вытянутых рук по отношению к телу. Пропорции таковы:

·         от плеч до макушки к размеру головы = 1:1.618

·         от подбородка до верхней губы и от нее до носа = 1:1.618

·         от пупка до макушки к отрезку от плеч до макушки = 1:1.618

·         от пупка до колен и от колен до ступней = 1:1.618

Фамилии учащихся: …………………………………………………………………………

Ход практической части:

ЧАСТЬ 1.

1.Заполните  таблицу, выполните измерения роста, высоты от пупка до макушки головы, высоты  от пупка до пятки , занесите данные  в таблицу.

2.Вычислите   отношения

3.  Сделайте   сравнения, вычислите  % учеников, отношение которых равно золотому сечению.

ЧАСТЬ 2.

 1. Сделайте   из бумаги правильный прямоугольник.

 Соотношения сторон a: b =c : a =1,618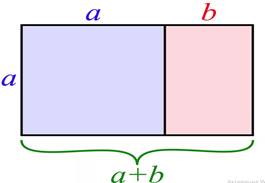

где  с =a+b

2. Вычислите стороны  a  и b, для этого составьте уравнение и решите его, за основу расчета возьмите  с, т.е длину  листа бумаги, тогда ширина a =c/1,6

3. Отрежьте от этого прямоугольника  квадрат со стороной a, затем отрежьте от оставшегося  прямоугольника квадрат со стороной   b, и т.д.

4. Заполните таблицу

Cделайте вывод о соотношении a: b, полученных прямоугольников

ЧАСТЬ 3

На новом листе бумаги, используя таблицу  части 2 , постройте спираль Фибоначчи.